What is the binary number for 15
Answers
Answer:
111
Step-by-step explanation:
notice that 1000 in binary is 16, as 1000 in binary would be 2^4 = 16. If you subtract 1 from 1000 in binary, you get 111.
If this helped please give brainliest.
Related Questions
Please help I’ll give you brainiest :).

Answers
Answer:I’m so sorry I can’t help
Step-by-step explanation:
Answer:
i think its a
Step-by-step explanation:
What is the percent of decrease from 25 to 15?
Round your answer to the nearest tenth.
Enter your answer in the box.
%
Answers
50%=12.5
10%=2.5
12.5(50%) +2.5(10%)= 50%(15)
so the answer is 60%
Answer:
40% is correct
Step-by-step explanation: I took the test in k12 if you guys are wondering and yes it shows 40%.
Without any programs, form a polynomial function of degree 2 with zero points x = 1 and x = 3 and whose graph passes through the point (5, 4).
BALIIIISS AND BALIIS
Answers
Answer:
\(y= \frac12 x^2 -2x +\frac32\)
Step-by-step explanation:
From the two zeroes, you can tell that the polynomial factors as \(y= A(x-1)(x-3)\). You have still one degree of freedom (determining how wide the parabola is. You can determine it with the other condition:
\(4 = A(5-1)(5-3) \rightarrow 4= A(4)(2) \rightarrow A= \frac12\)
Your function is \(y= \frac12 (x-1)(x-3) = \frac12 x^2 -2x +\frac32\)
A place kicker in pro football has a 77% probability of making a field goal over 40 yards, and each attempted field goal is independent. If the kicker made his first two but missed his third attempt and is now trying for his fourth field goal of the game to win in overtime, what is the probability that his team will win the game
Answers
The probability that the team will win the sport is 77%.
Given that an area kicker in pro football incorporates a 77% probability of creating a field goal over 40 yards and every attempt field goal is independent.
Probability is how something is likely to happen. The probability of a happening is calculated by the probability formula by simply dividing the favorable number of outcomes by the overall number of possible outcomes.
So, his team will win the sport if he makes a goal otherwise loses.
Therefore, the Probability that his team will win the sport P[E] =P[making a field goal]
P[E]=77%
Hence, the probability that the team will win the sport when making a field goal is 77%.
Learn more about probability from here brainly.com/question/993963
#SPJ4
calculate the taylor polynomials 2 and 3 centered at =0 for the function ()=16tan().
Answers
Taylor polynomials of degree 2 and 3 centered at x = 0 for the function f(x) = 16tan(x) are:
P2(x) = 16x + 8x^2
P3(x) = 16x + 8x^2
To find the Taylor polynomials centered at x = 0 for the function f(x) = 16tan(x), we can use the Taylor series expansion for the tangent function and truncate it to the desired degree.
The Taylor series expansion for tangent function is:
tan(x) = x + (1/3)x^3 + (2/15)x^5 + (17/315)x^7 + ...
Using this expansion, we can find the Taylor polynomials of degree 2 and 3 centered at x = 0:
Degree 2 Taylor polynomial:
P2(x) = f(0) + f'(0)(x - 0) + (1/2!)f''(0)(x - 0)^2
= 16tan(0) + 16sec^2(0)(x - 0) + (1/2!)16sec^2(0)(x - 0)^2
= 0 + 16x + 8x^2
Degree 3 Taylor polynomial:
P3(x) = P2(x) + (1/3!)f'''(0)(x - 0)^3
= 0 + 16x + 8x^2 + (1/3!)(48sec^2(0)tan(0))(x - 0)^3
= 16x + 8x^2
Therefore, the Taylor polynomials of degree 2 and 3 centered at x = 0 for the function f(x) = 16tan(x) are:
P2(x) = 16x + 8x^2
P3(x) = 16x + 8x^2
Learn more about taylor polynomials at https://brainly.com/question/31978863
#SPJ11
What are the coordinates of the point on the directed line segment from (-8, 5)(−8,5) to (4, -3)(4,−3) that partitions the segment into a ratio of 5 to 3?
Answers
Answer:
(2, -7/2)
Step-by-step explanation:
According to the midpoint theorem;
M(X, Y) = [(ax1+bx2/a+b), ay1+by2/a+b ]
(x1, y1) and (x2, y2) are the coordinates
a:b is the given ratio
Given the following
Coordinate of the line segment (-8, 5) and (4, -3)
Ratio: 5:3
Get the X coordinate;
X = ax1 + bx2 / a+b
X = 5(-8) + 3(4)/5+3
X = -40+12/8
X = -28/8
X = -7/2
Get the Y coordinate
Y = ay1 + by2 / a+b
Y = 5(5) + 3(-3)/5+3
Y = 25-9/8
Y = 16/8
Y = 2
Hence the required coordinate is (2, -7/2)
help help u will get 11 points !

Answers
Answer:
30
Step-by-step explanation:
all triangles =180
because 180 -120 =60whch is the missing inside angle
and we know that this is a right angle
so we subtact what we know to find what we dont
180-(60+90)=30
(150)
180-150=30
Answer:
30
Step-by-step explanation:
Consider a single spin of the spinner. a spinner contains 4 equal sections: 1, 2, 4 and 3. sections 1 and 4 are shaded. the spinner is pointed at number 2. which events are mutually exclusive? select two options.
Answers
To determine which events are mutually exclusive, we need to identify the events that cannot occur at the same time.
The options for the events are: Landing on a shaded section Landing on an even number Landing on an odd number Landing on a section that is not shaded Now let's analyze the options Landing on a shaded section (1 or 4) and landing on an even number (2 or 4) are mutually exclusive, as they cannot occur at the same time.
Landing on a shaded section (1 or 4) and landing on an odd number (1 or 3) are not mutually exclusive, as they can occur at the same time if the spinner lands on section 1. The mutually exclusive events in this scenario are: Landing on a shaded section Landing on an even number
To know more about exclusive visit:
https://brainly.com/question/32256304
#SPJ11
From the given information, the two mutually exclusive events are:
1. Landing on a shaded section (sections 1 or 4)
2. Landing on an even number (sections 2 or 4)
Therefore, these are the two options that are mutually exclusive based on the spinner's configuration.
The term "mutually exclusive" refers to events that cannot occur at the same time. In this case, we need to determine which events on the spinner are mutually exclusive given the information provided.
To start, let's list the numbers on the spinner: 1, 2, 4, and 3. We are told that sections 1 and 4 are shaded, and the spinner is pointed at number 2.
Event 1: Landing on a shaded section.
This event includes landing on either section 1 or section 4. Since these sections are shaded, they cannot occur simultaneously with any other section on the spinner.
Event 2: Landing on an odd number.
This event includes landing on either section 1 or section 3. These sections are mutually exclusive with the even numbers, which are 2 and 4.
Event 3: Landing on a multiple of 4.
This event includes landing on section 4. Since section 4 is shaded, it cannot occur simultaneously with any other section on the spinner.
Event 4: Landing on an even number.
This event includes landing on either section 2 or section 4. These sections are mutually exclusive with the odd numbers, which are 1 and 3.
Learn more about mutually exclusive from the link:
https://brainly.com/question/12961938
#SPJ11
"Match the justifaction with each step"

Answers
I also want to know the answer...........................................
help pretty pleasee

Answers
Answer:
so you just put both equations together and do the equation like so hers an example
explanation: (7x-22)-(4x+5)= but if your looking for X
x=9
Find the equation of the line of the below:

Answers
Answer:
y = -x + 9
Step-by-step explanation:
Slope Formula: \(m=\frac{y_2-y_1}{x_2-x_1}\)
Slope-Intercept Form: y = mx + b
m - slope
b - y-intercept
Step 1: Define
(0, 9) y-intercept
(9, 0) x-intercept
Step 2: Find slope m
\(m=\frac{0-9}{9-0}\)
\(m=\frac{-9}{9}\)
\(m=-1\)
y = -x + b
Step 3: Write linear equation
y = -x + 9
Answer:
y = -x + 9
Step-by-step explanation:
Slope Formula:
Slope-Intercept Form: y = mx + b
m - slope
b - y-intercept
Step 1: Define
(0, 9) y-intercept
(9, 0) x-intercept
Step 2: Find slope m
y = -x + b
Step 3: Write linear equation
y = -x + 9
Out of 290 racers who started the marathon, 268 completed the race, 15 gave up, and 7 were disqualified. What percentage did not complete the marathon
Answers
The percentage that did not complete the marathon is 7.59%
What percentage did not complete the marathonFrom the question, we have the following parameters that can be used in our computation:
Participants = 290
Completed = 268
using the above as a guide, we have the following:
Percentage = (Participants - Completed)/Participants * 100%
substitute the known values in the above equation, so, we have the following representation
Percentage = (290 - 268)/290 * 100%
Evaluate
Percentage = 7.59%
Hence, the percentage that did not complete the marathon is 7.59%
Read more about percentage at
https://brainly.com/question/28398580
#SPJ4
37) Kali ran 17 miles less than Alberto last
week. Kali ran 9 miles. How many miles
did Alberto run?
Answers
STAN LOONA FOR A BETTER LIFE OR ELSE U WILL BE SINGLE FOR THE REST OF UR LIFE
Answers
We as we see this question is quite simple
first we find the vocabulary which is in simple text slang and convert it formally to english...
Next we find that this question makes no sense so g'day
First look at the equipment
I need help on this question

Answers
Answer:
c
Step-by-step explanation:
Josh has $40 and is saving $10 a day. Sal has
$160 and is spending $5 a day. After how
many
days will they have the same amount of
money?
Answers
Answer:
day eight!!
Step-by-step explanation:
Josh --> starts with $40, saving $10
Sal --> starts with $160, spending $5
day one: josh: $50, sal: $155
day two: josh: $60, sal: $150
day three: josh: $70, sal: $145
day four: josh: $80, sal: $140
day five: josh: $90, sal: $135
day six: josh: $100, sal: $130
day seven: josh: $110, sal: $125
day eight: josh: $120, sal: $120
The picture shows the top view of a piece of glass. Which equations can be used to find the area, in square feet, of the piece of glass? Select all that apply. A. A = 2 1 2 × 4 = 2 1 2 × 4 B. A = 5 2 + 4 = 5 2 + 4 C. A = ( 2 1 2 + 2 1 2 ) + ( 4 + 4 ) = ( 2 1 2 + 2 1 2 ) + ( 4 + 4 ) D. A = 5 2 × 4 = 5 2 × 4 E. A = ( 2 × 2 1 2 ) + ( 2 × 4 ) = ( 2 × 2 1 2 ) + ( 2 × 4 ) F. A = 2 1 2 + 4 ]
Answers
options B, D, and E are correct. Option A is incorrect because it uses the wrong length measurement.
what is a rectangle?
A rectangle is a four-sided flat shape with straight sides, where opposite sides are parallel and equal in length. It has four right angles (90-degree angles) at each corner. The length and width of a rectangle are its two main dimensions, and the area of a rectangle is calculated by multiplying its length by its width.
Based on the picture, we can see that the glass has a rectangular shape with dimensions of 4 feet and 5 2/12 feet. Therefore, the equations that can be used to find the area, in square feet, of the piece of glass are:
B. A = 5 2/12 + 4 = 9 2/12 = 7/3 square feet
D. A = 5 2/12 × 4 = 20 1/3 square feet
E. A = (2 × 2 1/2) + (2 × 4) = 9 square feet
Therefore, options B, D, and E are correct. Option A is incorrect because it uses the wrong length measurement. Option C is incorrect because it adds the dimensions instead of multiplying them. Option F is also incorrect because it adds the dimensions instead of multiplying.
Options B, D, and E correctly calculate the area of the glass by multiplying the length by the width. Option B adds the length and width before multiplying them, while option D multiplies the length and width directly.
To learn more about rectangle from the given link:
https://brainly.com/question/29123947
#SPJ1
what is 5 * 4 + 6 - 5 * 5 * 7 / 8 * 6 - 8 + 2
Answers
The answer is -445/4 in improper fraction form, -111 1/4 as a mixed fraction, and -111.25 in decimal form.
Answer:
-111.25
Step-by-step explanation:
Need help with the answer it’s confusing

Answers
16±0.12
Step-by-step explanation:
%uncertainity=uncertainity÷measured value×100%
0.75×16=100x
x=12÷100
x=0.12
ANS;16±0.12
14. (10.0 points) Given f(x)=sin(2πx), when x = 0.3, f(x) = 0.951057. Approximate the value of f(0.2) using the first two terms in the Taylor series and Vx=0.1. (Write your answer to 6 decimal points).
Answers
Given the function f(x)=sin(2πx), with x = 0.3, f(x) = 0.951057. The objective is to approximate the value of f(0.2) using the first two terms in the Taylor series and Vx=0.1.
We know that the Taylor series for a function f(x) can be written as:f(x)=f(a)+f′(a)(x−a)+f′′(a)2(x−a)2+…+f(n)(a)n!(x−a)n+…The first two terms of the Taylor series are given by:f(x)=f(a)+f′(a)(x−a)The first derivative of f(x) is given by:f′(x)=2πcos(2πx)On substituting x = a = 0.1, we get:f′(0.1) = 2πcos(2π * 0.1) = 5.03118603447The value of f(x) at a=0.1 is given by:f(0.1) = sin(2π * 0.1) = 0.587785252292With a=0.1, the first two terms of the Taylor series become:f(x)=0.587785252292+5.03118603447(x−0.1) = 0.587785252292+0.503118603447x−0.503118603447×0.1Using x=0.2 and substituting the values of a and f(a) in the equation above, we get:f(0.2)=0.587785252292+0.503118603447*0.2−0.503118603447×0.1=0.712261After approximating the value of f(0.2) using the first two terms in the Taylor series,
we can conclude that the value of f(0.2) = 0.712261 with a = 0.1, with an error of approximately 0.012796.
To know more about Taylor series visit
https://brainly.com/question/32235538
#SPJ11
What is 1/8 as a decimal?
Answers
Answer:
0.125
Step-by-step explanation:
convert to decimal, then divide
Write the quadratic equation in standard form.
Then solve using the quadratic formula.
1+ 4x + 3x2 = 0
HELPP
Answers
Answer:
x = − 1 3 − 1
Step-by-step explanation:
Solve the equation for x by finding a , b , and c of the quadratic then applying the quadratic formula. x = − 1 3 − 1
1. Mario Orozco's monthly gross pay
is $7,500.00.
Housing expenses for
November were:
Mortgage Payment
Real Estate Taxes
Insurance
Electricity
Heating Fuel
Telephone
Cable Service
a. Total Housing Costs
$936.30
272.00
129.50
87.50
160.50
39.50
89.99
Answers
The total housing costs for Mario Orozco in November were $1,715.29.
How do we calculate the total housing cost?To find the total housing costs for Mario Orozco, you simply add up all the expenses in November that has been provided;
$936.30 (Mortgage Payment)
$272.00 (Real Estate Taxes)
$129.50 (Insurance)
$87.50 (Electricity)
$160.50 (Heating Fuel)
$39.50 (Telephone)
$89.99 (Cable Service)
936.30 + 272.00 +129.50 + 87.50 + 160.50 + 39.50 + 89.99 = 1,715.29
Find more exercises on total cost;
https://brainly.com/question/29085757
#SPJ1
Giving a test to a group of students, the grades and gender are summarized below ABCTotalMale321419Female542029Total863448If one student is chosen at random,Find the probability that the student was male OR got a/an "C". Round to at least 3 decimal places.
Answers
0.813
Explanations:Probability is the likelihood or chance that an event will occur. The probability that the student was male OR got a/an "C" is as shown:
P(male or a C) = Pr(male) + Pr(C) - Pr(male and C)
Pr(male U C) = Pr(male) + Pr(C) - Pr(male n C)
Given the following probabilities
\(\begin{gathered} Pr(male)=\frac{19}{48} \\ Pr(C)=\frac{34}{48} \\ Pr(male\text{ U C})=\frac{14}{48} \end{gathered}\)Substitute the probability to have:
\(\begin{gathered} Pr(male\text{ }U\text{ C})=\frac{19}{48}+\frac{34}{48}-\frac{14}{48} \\ Pr(male\text{ }U\text{ C})=\frac{19+34-14}{48} \\ Pr(male\text{ }U\text{ C})=\frac{39}{48} \\ Pr(male\text{ }U\text{ C})=\frac{13}{16} \\ Pr(male\text{ }U\text{ C})=0.813 \end{gathered}\)Hence the probability that the student was male OR got a/an "C" is 0.813
3- Find all values of Z such that e² = 2+i√3
Answers
The values of Z such that e² = 2 + i√3 are Z = ln(2 + i√3) + 2πik, where k is an integer.
To find the values of Z, we can start by expressing 2 + i√3 in polar form. Let's denote it as re^(iθ), where r is the modulus and θ is the argument.
Given: 2 + i√3
To find r, we can use the modulus formula:
r = sqrt(a^2 + b^2)
= sqrt(2^2 + (√3)^2)
= sqrt(4 + 3)
= sqrt(7)
To find θ, we can use the argument formula:
θ = arctan(b/a)
= arctan(√3/2)
= π/3
So, we can express 2 + i√3 as sqrt(7)e^(iπ/3).
Now, we can find the values of Z by taking the natural logarithm (ln) of sqrt(7)e^(iπ/3) and adding 2πik, where k is an integer. This is due to the periodicity of the logarithmic function.
ln(sqrt(7)e^(iπ/3)) = ln(sqrt(7)) + i(π/3) + 2πik
Therefore, the values of Z are:
Z = ln(2 + i√3) + 2πik, where k is an integer.
The values of Z such that e² = 2 + i√3 are Z = ln(2 + i√3) + 2πik, where k is an integer.
To know more about polar form visit
https://brainly.com/question/30824428
#SPJ11
A state highway patrol official wishes to estimate the percentage/proportion of drivers that exceed the speed limit traveling a certain road.
A. How large a sample is needed in order to be 95% confident that the sample proportion will not differ from the true proportion by more than 3 %? Note that you have no previous estimate for p.
B. Repeat part (A) assuming previous studies found that the sample percentage of drivers on this road who exceeded the speed limit was 65%
Answers
A) Approx. 1067 is the required sample size to ensure 95% confidence that the sample proportion will not differ from the true proportion by more than 3%.
B) When the previous estimate is 65%, approx. 971 is the sample size needed to achieve 95% confidence that the sample proportion will not differ by more than 3% from the true proportion.
How to calculate the sample size needed for estimating the proportion?To determine the sample size needed for estimating the proportion of drivers exceeding the speed limit, we can use the formula for sample size calculation for proportions:
n = (Z² * p * (1 - p)) / E²
where:
n = the sample size.
Z = the Z-value associated with the confidence level of 95%.
p = the estimated proportion or previous estimate.
E = the maximum allowable error, which is 3% or 0.03.
We calculate as follows:
A. No previous estimate for p is available:
Here, we will assume p = 0.5 (maximum variance) since we don't have any prior information about the proportion. So, adding the values into the formula:
n = (Z² * p * (1 - p)) / E²
n = ((1.96)² * 0.5 * (1 - 0.5)) / 0.03²
n= (3.842 * 0.5 * (0.5))/0.03²
n = (1.9208*0.5)/0.0009
n ≈ 1067.11
Thus, to be 95% confident that the sample proportion will not differ from the true proportion by more than 3%, a sample size of approximately 1067 is required.
B. Supposing previous studies found that the sample percentage of drivers who exceeded the speed limit is 65%:
Here, we have a previous estimate of p = 0.65:
Putting the values into the formula:
n = (Z²* p * (1 - p)) / E²
n = ((1.96)² * 0.65 * (1 - 0.65)) / 0.03²
n= (3.842 * 0.65 *(0.35))/0.0009
n ≈ 971
Hence, with the previous estimate of 65%, a sample size of approximately 971 is necessary to be 95% confident that the sample proportion will not differ from the true proportion by more than 3%.
Learn more about sample size calculation at brainly.com/question/30647570
#SPJ4
an lti system has the frequency response function h(ω)=1/(jω 3). compute the output if the input is
Answers
The output of the LTI system with frequency response function \(h(w) = 1/(jw^3)\), given an input\(x(t)\), is:
\(y(t)\)= inverse Fourier transform of \([1/(jw^3) X(w)]\)
To compute the output of an LTI system with frequency response function \(h(w) = 1/(jw^3)\), given an input x(t), we can use the Fourier transform:
\(H(w)\) = Fourier transform of \(h(t)\)
\(X(w)\) = Fourier transform of \(x(t)\)
\(Y(w) = H(w) X(w)\)
\(Y(w)\) is the Fourier transform of the output \(y(t)\).
Using the given frequency response function, we have:
\(H(w) = 1/(jw^3)\)
Taking the Fourier transform of the input \(x(t)\), we have:
\(X(w)\) = Fourier transform of \(x(t)\)
And multiplying \(H(w)\) and\(X(w)\), we get:
\(Y(w) = H(w) X(w) = 1/(jw^3) X(w)\)
Taking the inverse Fourier transform of \(Y(w)\), we get the output \(y(t)\):
\(y(t)\) = inverse Fourier transform of \(Y(w)\)
For similar questions on frequency
https://brainly.com/question/30466268
#SPJ11
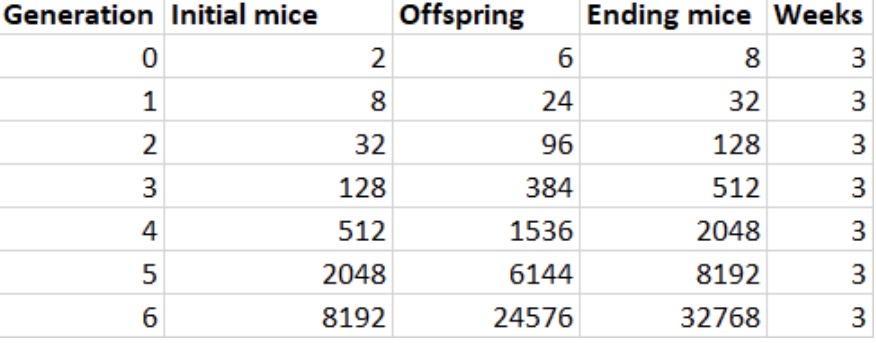
In exactly one year, how many mice would there be at school? EXPLAIN FULLY AND SHOW ALL WORK:Equation: Y=a(4)^xWhere:a is the initial value (when the generation = 0)x is the generation.


Answers
We know that each generation takes approximately 3 weeks, then, we can estimate how many generations we do have in one year, remember that one year has
\(1\text{ year }\approx52.14286\text{ weeks}\)Then, in one year we have
\(\frac{52.14286}{3}=17.383\text{ generations}\)In the real world, we can't have half of a generation or a decimal generation, then, let's approximate it to the nearest integer, in that case, 17 generations.
We have the expression that predicts the number of mice, then we can use that equation to find the result for 17 generations:
\(\begin{gathered} \text{ Initial Mice:} \\ f(x)=2\cdot4^x \end{gathered}\)Evaluate that at x = 17
\(\begin{gathered} \text{ Initial Mice} \\ f(x)=2\cdot4^x\Rightarrow f(17)=2\cdot4^{17}\Rightarrow3.44×10^{10} \end{gathered}\)With an offspring of
\(\begin{gathered} \text{ Offspring} \\ f(x)=6\cdot4^x\Rightarrow f(17)=6\cdot4^{17}=1.03×10^{11} \end{gathered}\)And the ending mice
\(\begin{gathered} \text{ Ending Mice} \\ f(x)=8\cdot4^x\Rightarrow f(17)=8\cdot4^{17}=1.37×10^{11} \end{gathered}\)Therefore, the final answer is
\(\text{ Ending mice = }1.37\times10^{11}\)Plsssss Help!!!
Determine whether each statement is true or false given the linear functions modeled by table A table and table B.


Answers
T F T
Step-by-step explanation: JUST DID THE TEST
PLzz HeLP Moi x(y-xy), where x= -5 and y= -2