what is the correct order of the rational numbers and table from least to greatest? Use the number line to help you.

Answers
Answer:
The second, I believe.
Step-by-step explanation:
Related Questions
A baseball is 1.75 times the size of a golf ball. If the golf ball is 1.68 inches in
diameter, what is the diameter of the baseball?
Answers
Answer:
2.94 in
Step-by-step explanation:
Pls help I’ll brainlest and add extra points do all of them

Answers
Answer:
17/16= 1.06 (rounded)
16/17= 0.94 (rounded)
9/45= 0.2
5/13= 0.38 (rounded)
-28/35= -0.8
15/20= 0.75
Step-by-step explanation: Hope this helps
please help.
definitions: 1. definition of right triangle
2. definition of isosceles TrianglesReflexive
3. HL
4. definition of perpendicular
5. CPCTC
6. reflexive

Answers
From the two column proof below, we have seen ∠BAC ≅ ∠DAC by CPCTC
How to solve two column proof problems?The two column proof to show that ∠BAC ≅ ∠DAC is as follows:
Statement 1: ΔABD is Isosceles with base BD, AC ⊥ BD
Reason 1: Given
Statement 2: AB ≅ AD
Reason 2: Definition of isosceles Triangles
Statement 3: ∠1 and ∠2 are right angles
Reason 3: Definition of perpendicular
Statement 4: AC ≅ AC
Reason 4: Reflexive Property
Statement 5: ΔABC and ΔADC are right triangles
Reason 5: Definition of right triangle
Statement 6: ΔABC ≅ ΔADC
Reason 6: HL Congruency
Statement 7: ∠BAC ≅ ∠DAC
Reason 7: CPCTC
Read more about two column proof at; brainly.com/question/1788884
#SPJ1
3 Jack walk from Santa Clara to Polo Allo. Il took I hour 25 min to walk from Santa Clot to Los Altos. Than it took 25 minute of wal from los altos to Palo buto. He arrived in Palo alto at 2:45 P.M. of what time die Santa Clara ? he leave Santa clara
Answers
The time Jack left Santa Clara is 1 : 55 pm
What is word problem?A word problem in math is a math question written as one sentence or more. These statements are interpreted into mathematical equation or expression.
The time for Jack to walk to lose Altos is 25 min and he uses another 25mins to work to Palo alto.
Therefore, the total time he spent is
25mins + 25 mins = 50 mins
He arrived Palo at 2 :45 pm, therefore the time he left Santa Clare will be ;
2:45 pm = 14 :45
= 14:45 - 50mins
= 13:55
= 1 : 55pm
Therefore he left at 1:55 pm
learn more about word problem from
https://brainly.com/question/21405634
#SPJ1
What is the ratio of number of students receiving and C and the number of students receiving an A
Answers
The ratio of number of students receiving and C and the number of students receiving an A is 4 to 1.
What is ratio and proportion?When comparing two quantities of the same kind, ratio is utilised. For two numbers, a and b, the ratio formula is written as a: b or a/b. Two or more ratios are said to be in proportion if they are all equal. Fractions are the foundation of the concepts of ratio and proportion. The fundamental building blocks of numerous other mathematical notions are ratio and proportion. In many everyday situations, such as when comparing heights, weights, distances, or times, or when adding components to a recipe, ratio and proportion can be used to help us solve our difficulties.
From the table we observe that the number of students receiving C is: 12.
The number of students receiving A is 3.
The ratio of number of students receiving and C and the number of students receiving an A is:
C / A = 12 / 3 = 4 / 1
Hence, the ratio of number of students receiving and C and the number of students receiving an A is 4 to 1.
Learn more about ratio here:
https://brainly.com/question/13419413
#SPJ1
The correct question is:

The price of a small cabin is $100,000. The bank requires a 5% down payment. The buyer is offered two mortgage options: 20-year fixed at 8% or 30-year fixed at 8%. Calculate the amount of interest paid for each option. How much does the buyer save in interest with the 20-year option?
Answers
The buyer saves $76000 in interest with the 20-year option.
What is simple interest formula ?
If P be the principal amount, t be the time
And R be the rate of interest.
Then, Simple Interest(S.I.) = (P×R×t)/100
What are the required results ?The down payment is of 5%
The price of the small cabin is $100000
Hence the principal is 95% of the price.
P = $(100000×0.95) = $95000
For 20 years option,
P = $95000 , R = 8%, t = 20 yrs
S.I. = (95000×8×20)/100 = 152000
So, the amount of interest paid for the 20 years is $152000
For 30 years option,
P =$95000, R=8%, t = 30 yrs
S.I. = (95000×8×30)/100 = 228000
So, the amount of interest paid for the 30 years is $228000
∴ The buyer saves $(228000-152000) = $76000 in interest with the 20 years option.
Learn more about simple interest here :
https://brainly.com/question/1173061
#SPJ10
A straw is placed inside a rectangular box that is 4 inches by 2 inches by 10 inches, as
shown. If the straw fits exactly into the box diagonally from the bottom left corner to
the top right back corner, how long is the straw? Leave your answer in simplest
radical form.
10 in.
4 in.
2 in.

Answers
Answer:
The length of the straw in the simplest radical form is \(2\sqrt{30}\) inches
Step-by-step explanation:
The length of the straw can be calculated as follow
The first step is to calculate the diagonal of the base of the rectangular box by using Pythagorean theorem
\(c^{2}=a^{2}+b^{2}\)
Where \(c\) is the base diagonal or the hypotenuse, \(a\) is the short leg, \(b\) is the long leg
Substitute \(2\) for \(a\), \(4\) for \(b\) in the Pythagorean theorem
\(c^{2}=2^{2}+4^{2}\)
Simplify the right side of the equation
\(c^{2}=4+16\)
\(c^{2}=20\)
Take the square root of the right side to get the value of \(c\)
\(c=\sqrt{20}\)
Factor \(20\) by \(4\)
\(c=\sqrt{4\times 5}\)
Substitute \(2^{2}\) for 4
\(c=\sqrt{2^{2}\times 5}\)
Rewrite the value of \(c\) in the simplest radical form
\(c=2\sqrt{5}\)
Since the value of \(c\) is \(2\sqrt{5}\), then the length of the diagonal of the base is
\(2\sqrt{5}\) inches
The second step is to calculate the length of the straw by using Pythagorean theorem
\(c^{2}=a^{2}+b^{2}\)
Where \(c\) is the diagonal from the bottom left corner to the top right back corner or the hypotenuse, \(a\) is the short leg, \(b\) is the long leg
Substitute \(2\sqrt{5}\) for \(a\), \(10\) for \(b\) in the Pythagorean theorem
\(c^{2}=(2\sqrt{5})^{2}+10^{2}\)
Simplify the right side of the equation
\(c^{2}=20+100\)
\(c^{2}=120\)
Take the square root of the right side to get the value of \(c\)
\(c=\sqrt{120}\)
Factor \(120\) by \(4\)
\(c=\sqrt{4\times 30}\)
Substitute \(2^{2}\) for 4
\(c=\sqrt{2^{2}\times 30}\)
Rewrite the value of \(c\) in the simplest radical form
\(c=2\sqrt{30}\)
Since the value of \(c\) is \(2\sqrt{30}\), then the length of the diagonal from the bottom left corner to the top right back corner or the hypotenuse is
\(2\sqrt{30}\) inches
Since the length of the diagonal from the bottom left corner to the top right back corner is \(2\sqrt{30}\) inches, then the length of the straw is \(2\sqrt{30}\) inches
Read more on Pythagorean theorem here
brainly.com/question/16426393
#SPJ1
Higher Order Thinking Morgan read
a thermometer at 7:00 P.M. The
temperature was 16°C. This temperature
was 9°C less than the temperature at
2:00 P.M. The temperature at 2:00 P.M.
was 10°C higher than the temperature at
8:00 A.M. What was the temperature at
8:00 A.M.?
Answers
The temperature at 8:00 A.M. was 15°C.
Using the given information:
1. At 7:00 P.M., the temperature was 16°C.
2. This temperature was 9°C less than the temperature at 2:00 P.M.
We can use this information to find the temperature at 2:00 P.M.:
Temperature at 2:00 P.M. = 16°C (temperature at 7:00 P.M.) + 9°C
Temperature at 2:00 P.M. = 25°C
3. The temperature at 2:00 P.M. was 10°C higher than the temperature at 8:00 A.M.
Now, we can find the temperature at 8:00 A.M.:
Temperature at 8:00 A.M. = 25°C (temperature at 2:00 P.M.) - 10°C
Temperature at 8:00 A.M. = 15°C
To know more about temperature refer to
https://brainly.com/question/24746268
Express cos M as a fraction in simplest terms.

Answers
\(\begin{array}{llll} \textit{using the pythagorean theorem} \\\\ a^2+o^2=c^2\implies a=\sqrt{c^2 - o^2} \end{array} \qquad \begin{cases} c=\stackrel{hypotenuse}{30}\\ a=\stackrel{adjacent}{MN}\\ o=\stackrel{opposite}{18} \end{cases} \\\\\\ MN=\sqrt{ 30^2 - 18^2} \implies MN=\sqrt{ 576 }\implies MN=24 \\\\[-0.35em] ~\dotfill\\\\ \cos(M )=\cfrac{\stackrel{adjacent}{24}}{\underset{hypotenuse}{30}} \implies \cos(M)=\cfrac{4}{5}\)
Find the side length of a square with area 16/49 square inches
Answers
Answer: the correct answer is S= 4/7 inches.
Which algebraic expression is a polynomial?

Answers
The algebraic expression that is a polynomial is -6x³ + x² - √5
How to know a polynomial?Polynomials are algebraic expressions that consist of variables and coefficients.
In a simpler term a polynomial can have constants, variables and exponents, but never division by a variable.
Therefore, the polynomial among the options is as follows:
-6x³ + x² - √5
learn more on polynomial here: https://brainly.com/question/12401404
#SPJ1
Which equation accurately represents this statement? Select three options. Negative 3 less than 4.9 times a number, x, is the same as 12.8. Negative 3 minus 4.9 x = 12.8 4.9 x minus (negative 3) = 12.8 3 + 4.9 x = 12.8 (4.9 minus 3) x = 12.8 12.8 = 4.9 x + 3
Answers
The value of x in the statement negative 3 less than 4.9 times a number x is the same as 12.8 is 2.
What is a numerical expression?A numerical expression is a mathematical statement written in the form of numbers and unknown variables. We can form numerical expressions from statements.
Given a statement negative 3 less than 4.9 times a number, x, is the same as 12.8 this can be numerically expressed as,
4.9x - (- 3) = 12.8.
4.9x + 3 = 12.8
4.9x = 12.8 - 3.
4.9x = 9.8.
x = 9.8/4.9.
x = 2.
learn more about numerical expressions here :
https://brainly.com/question/29199574
#SPJ1
If m and n are positive integers and m^2 - n^2 = 9, which of the following could be the value of
n?
A) 1
B) 16
C) 9
D) 4
Answers
Answer:
4
Problem:
If m and n are positive integers and m^2 - n^2 = 9, which of the following could be the value of
n?
A) 1
B) 16
C) 9
D) 4
Step-by-step explanation:
One approach would be to plug in the choices and see.
If n=1, then we have m^2-1=9.
This would give m^2=10 after adding 1 on both sides. There is no integer m when squared would give us 10. ( Square root of 9 is a decimal )
If n=16, then we would have m^2-256=9.
This would give m^2=265 after adding 256 on both sides. There is no integer m when squared would give us 265. ( Square root of 265 is a decimal )
If n=9, then we would have m^2-81=9.
This would give m^2=90 after adding 81 on both sides. There is no integer m when squared would give us 90. ( Square root of 90 is a decimal )
If n=4, then we would have m^2-16=9.
This would give m^2=25 after adding 16 on both sides. There is an integer m when squared would give us 25. ( Square root of 25 is a 5)
one card is drawn from a pack of 52cards each of the 52 cards being equally likely to be drawn. what is the probability that the card drawn is a king?
Answers
The probability of drawing a king from a standard deck of 52 cards is 1/13.
In a standard deck of 52 playing cards, there are four kings: the king of hearts, the king of diamonds, the king of clubs, and the king of spades.
To find the probability of drawing a king, we need to determine the ratio of favorable outcomes (drawing a king) to the total number of possible outcomes (drawing any card from the deck).
The total number of possible outcomes is 52 because there are 52 cards in the deck.
The favorable outcomes, in this case, are the four kings.
Therefore, the probability of drawing a king is given by:
Probability = (Number of favorable outcomes) / (Number of possible outcomes)
= 4 / 52
= 1 / 13
Thus, the probability of drawing a king from a standard deck of 52 cards is 1/13.
This means that out of every 13 cards drawn, on average, one of them will be a king.
It is important to note that the probability of drawing a king remains the same regardless of any previous cards that have been drawn or any other factors.
Each draw is independent, and the probability of drawing a king is constant.
For similar question on probability.
https://brainly.com/question/7965468
#SPJ8
11 is greater than or equal to -13
Answers
Answer:
11 is greater than -13
Step-by-step explanation:
because -13 is a negative number
help me i need help pls you all are smart


Answers
Answer:
I know the answer of picture 1.
Step-by-step explanation:
\( \frac{28}{9} + \frac{9}{4} \)
\( \frac{28}{9} \times \frac{4}{4} + \frac{9}{4} \times \frac{9}{9} \)
\( \frac{112}{36} + \frac{81}{36} \)
\( \frac{ 112 + 81}{36} \)
\( \frac{193}{36} \)
Graph the solution set to this Inequality.
-2x + 9 < 51 12
Answers
Answer:
X<-2551.5
Step-by-step explanation:
-2x<5112-9
-2x/-2<5103/-2
x<-2551.5
Los organizadores de la Feria de Alimentos colocan un contenedor de agua que mide 2,76 metros de largo, por 23,5 decímetros de ancho y por 196 centímetros de alto. ¿Cuál es el volumen del contenedor? Expresa la respuesta en metros cúbicos con aproximación a centésimos.
Answers
The volume of the container is approximately 12.9516 cubic meters when rounded to the nearest hundredth.
To find the volume of the container, we need to multiply its length, width, and height. Let's convert the given measurements to meters to ensure consistent units.
The length of the container is 2.76 meters.
The width of the container is 23.5 decimeters, which is equal to 2.35 meters (since 1 decimeter = 0.1 meters).
The height of the container is 196 centimeters, which is equal to 1.96 meters (since 1 meter = 100 centimeters).
Now we can calculate the volume of the container:
Volume = Length × Width × Height
Volume = 2.76 meters × 2.35 meters × 1.96 meters
Volume ≈ 12.9516 cubic meters (rounded to four decimal places)
Therefore, the volume of the container is approximately 12.9516 cubic meters when rounded to the nearest hundredth.
for such more question on volume
https://brainly.com/question/6204273
#SPJ8
Please find the area of D, E, and F.
This would be appreciated :)

Answers
Answer:
Using graph for units
D=1/2(6)(9)=27 sq units
E=1/2(7)(6)=21 sq units
F=1/2(6)(8)=24 sq units
Step-by-step explanation:
Answer:
D=27 units, E=21 units, F=24 units
Step-by-step explanation:
The formula for area of a triangle is (BASE * HEIGHT)/2
For triangle D, the base is 9 units and the height is 6 units. Then you can apply the formula and do 9*6 which is 54 and then do 54/2 which is 27 units.
Similarly, the base for E is 6 units, and the height is 7 units. So you do 6*7 which is 42 and then do 42/2 which is 21 units.
Again, the base for F is 6 units, and the height is 8 units. Then again, using the formula, we can do 6*8 which is 48 and then do 48/2, which is 24 units.
Hopefully this helped!
what is the square root of -75 in simplified form
Answers
Answer:
5\(\sqrt{3}\)i
Step-by-step explanation:
\(\sqrt{-5(5)(3)}\) You can pull out a 5 and you are left with \(\sqrt{-1}\) and \(\sqrt{3}\).
The \(\sqrt{-1}\) = 1
5\(\sqrt{3}\) i
Answer: \(5\sqrt{3} i\)
Step-by-step explanation:
The square root of -75 is not a real number, because it is not possible to find a real number that when squared results in a negative number.
In mathematics, the square root of a number is defined as the number that, when multiplied by itself, equals the original number. For example, the square root of 4 is 2, because 2 x 2 = 4. Similarly, the square root of 9 is 3, because 3 x 3 = 9.
However, it is not possible to find a real number that, when squared, results in a negative number. This is because any real number multiplied by itself is always positive, regardless of whether the original number was positive or negative. For example, the square of -2 is 4, because (-2) × (-2) = 4, which is a positive number.
Double however, complex numbers are used to represent numbers that have a non-zero imaginary component, such as the square root of -1. Complex numbers are written in the form a + bi, where a and b are real numbers and i represents the imaginary unit.
Therefore, the square root of -75 can be written in simplified form as \(5\sqrt{3} i\), where \(i\) is the imaginary unit. This represents a complex number with a real component of 0 and an imaginary component of \(5\sqrt{3}\).
1. What would the slope of a line that is parallel to the line in the graph be?
(4,3)
X

Answers
keeping in mind that parallel lines have exactly the same slope, let's check for the slope of the line above, since a parallel line will have the same slope anyway
\((\stackrel{x_1}{4}~,~\stackrel{y_1}{3})\qquad (\stackrel{x_2}{1}~,~\stackrel{y_2}{-1}) ~\hfill \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{-1}-\stackrel{y1}{3}}}{\underset{run} {\underset{x_2}{1}-\underset{x_1}{4}}} \implies \cfrac{ -4 }{ -3 } \implies {\Large \begin{array}{llll} \cfrac{ 4 }{ 3 } \end{array}}\)
Determine if it is possible to form a triangle using the set of segments with the given measurements.
4.5 in., 5.6 in, 10 in.
a) No, adding all three sides does not add up to the correct measurements.
b) No, because two sides add up to less than the third one.
c) No, because two sides add up to more than the third one.
d) Yes, because two sides add up to less than the third one.
e) Yes, because two sides add up to more than the third one.
Answers
Answer:
e) Yes, because two sides add up to more than the third one.-------------------------
Apply the Triangle Inequality Theorem.
It states that:
For a triangle to exist, the sum of the lengths of any two sides must be greater than the length of the third side.We'll take the sum of two shortest sides and compare with the longest:
4.5 + 5.6 = 10.1 > 10It confirms the theorem, without testing the other two sides (which is obvious) so the answer is yes.
The matching answer choice is e).
SAT scores are normally distributed with a mean of 1,500 and a standard deviation of 300. An administrator at a college is interested in estimating the average SAT score of first-year students. If the administrator would like to limit the margin of error of the 82% confidence interval to 25 points, how many students should the administrator sample
Answers
Answer:
The appropriate solution is "259".
Step-by-step explanation:
According to the question,
\(\sigma = 300\)
\(M.E=25\)
At 82% CI,
\(\alpha = 0.18\)
Critical value,
\(Z_c=1.341\)
Now,
The sample size will be:
⇒ \(n=(Z_c\times \frac{\sigma}{E} )^2\)
By substituting the values, we get
\(=(1.341\times \frac{300}{25} )^2\)
\(=(1.341\times 12)^2\)
\(=259\)
Fill in the missing numbers to find an equivalent fraction to 3/4

Answers
hope this helps, have a nice day :))

ANYONE PLEASE HELP please i really needa answer this on time

Answers
Answer:
Line AB and the last AB
Step-by-step explanation:
Select the reason that best supports Statement 8 in the given proof.

Answers
Given
Ray RV bisects angle ABC
\(\begin{gathered} m\angle ABV=7x-3 \\ m\angle VBC=2x+7 \end{gathered}\)Find
Select the reason that best supports statement 8 in the given proof.
Explanation
Given
Ray RV bisects angle ABC
so , by definition of angle bisect
\(m\angle ABV=m\angle VBC\)by substitution ,
\(7x-3=2x+7\)addition property of equality
\(7x=2x+10\)now, by substitution property of equality ,
\(5x=10\)and last , by division property of equality
\(x=2\)Final Answer
Therefore , the correct option is B.
help me pleasee!!
thank you
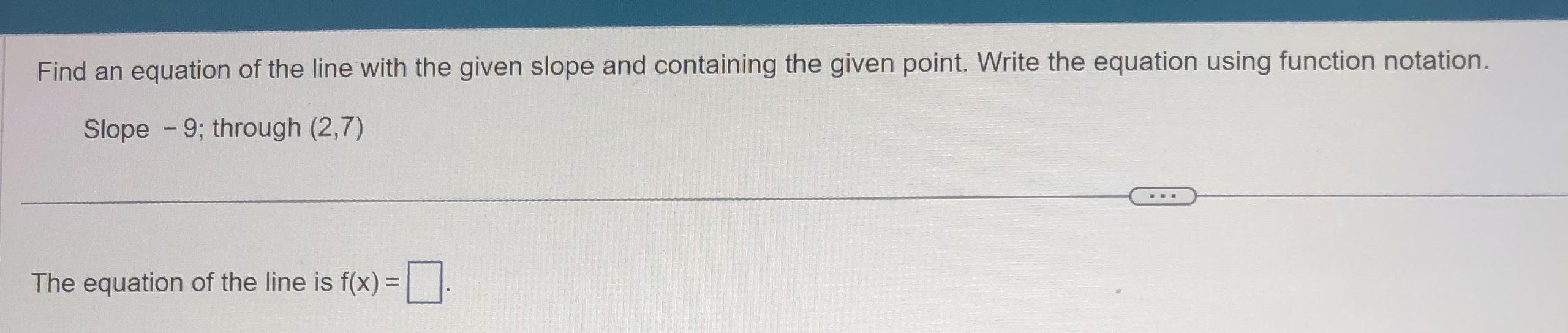
Answers
Answer:
f(x) = -9 * (x - 2) + 7
f(x) = -9x + 18 + 7
f(x) = -9x + 25
a waitress wondered if there was an association between the type of food and the type of drink customers ordered. the results are displayed below. based on the graph, is there an association between food ordered and drink ordered? there is an association because the distribution of drinks ordered differs among the food groups. there is an association because the distribution of drinks ordered is the same among the food groups. there is no association because the distribution of drinks ordered differs among the food groups. there is no association because the distribution of drinks ordered is the same among the food groups.
Answers
Yes, there is an association between food ordered and drink ordered because the distributive property of drinks ordered differs among the food groups.
Yes, there is an association between food ordered and drink ordered, as evidenced by the graph. The graph shows the distribution of drinks ordered among the various food groups, and it can be seen that the distribution differs among the food groups. For example, beer is the most popular drink ordered when burgers are the food ordered, while soda is the most popular drink when salads are the food ordered. This indicates that customers are more likely to order certain drinks depending on the type of food they are ordering, showing an association between food ordered and drink ordered.
Learn more about distributive property here
https://brainly.com/question/5637942
#SPJ4
Will all slices created by a slicing plane that passes through a sphere be the same size
Answers
Answer:
The suggestion proposed considering special cases, so that’s what we’ll do.
One special case we could consider is when x=0. If h=r, then we have a hemisphere. You may have learnt that the surface area of a sphere is 4πr2, so the answer in this case is 2πr2. Likewise, we can consider the most extreme cases: when h=2r, we get an area of 4πr2 (the entire sphere), and when h=0, we get zero area.
So if we do manage to get a general formula, we will be able to check it in these special cases.
Another possible idea when x=0 is to consider what happens when h is very small. In this case, the surface area looks a lot like a circle, but the radius of the circle does not seem particularly easy to work out, so maybe we’ll leave this one for a moment. (There are things we can do to approximate the radius using more advanced techniques, but they are currently beyond us.)
Another thing we could consider is the situation where h is very small. Then the part of the sphere between the planes looks very much like the frustum of a cone, and we know how to find the (surface) area of such a shape – see Cones.
If we recall our answer from that problem, we find the formulae for the surface area
π(R+r)s=π(R+r)hcosθ=π(R2−r2)sinθ.
Here, R is the radius of the base of the frustum, r is the radius of the top, h is the perpendicular height, s is the slant length and θ is the angle the slant makes with the vertical.
Step-by-step explanation:
Answer: no
Step-by-step explanation:
Construct a polynomial function that might have the graph. Yes, you guessed
it, there could be more than one answer! Only give me one of the possibilities.
Leave your answer in factored form.

Answers
There is a 'strike-through' root at -1 and a double root at 2, so the equation is of the form
\(y=a(x+1)^3 (x-2)^2\)
Since the y-intercept is 4,
\(4=a(0+1)^3(0-2)^2 \implies 4a=4 \implies a=1 \\ \\ \therefore \boxed{y=(x+1)^3 (x-2)^2}\)