What is the domain of the function on the graph
Answers
Answer:
The domain is all x-values or inputs of a function. hope this helps!
Step-by-step explanation:
Related Questions
Given a container that is 4.500 ft by 7.20 ft that is filled with water 5.00 inches deep. What is the volume of water in liters? (1 cubic centimeter = cc = cm^3 = 1 mL) How m
Answers
The volume of water in the container is approximately 383.098 liters.
How to find volume of water in liters?we first need to convert the dimensions of the container from feet to inches, so we have:
Length: 4.500 ft * 12 in/ft = 54.000 in
Width: 7.20 ft * 12 in/ft = 86.4 in
Depth: 5.00 in
The volume of water can be calculated by multiplying the length, width, and depth of the container, which gives:
Volume = 54.000 in * 86.4 in * 5.00 in = 23,364 cubic inches
To convert cubic inches to liters, we need to multiply by the conversion factor, which is 0.0163871 liters/cubic inch. This gives us:
Volume in liters = 23,364 cubic inches * 0.0163871 liters/cubic inch = 383.098 liters
Therefore, the volume of water in the container is approximately 383.098 liters.
Learn more about volume
brainly.com/question/1578538
#SPJ11
help please urgentttt
In which two sports are the players’ height distributions most alike? Explain your reasoning.

Answers
Following the steps below, use logarithmic differentiation to determine the derivative of the function f(x)= (1+2x)^1/x / sin(x)
a. Take the natural log of both sides and use properties of logarithms to expand the function: ln(f(x))=ln((1+2x)^(x1)csc(x)) b. Take the derivative implicitly: f(x)/f (x) = c. Solve for f ' (x) and replace f(x) with the original function definition: f' (x)=
Answers
From the logarithmic differentiation, function \(f(x) = \frac{( 1 + 2x)^{\frac{1}{x}}}{ sin(x)}\),
a) \( ln (f(x)) = \frac{1}{x} ln( 1 + 2x) - ln(sin(x))\\ \)
b) \( \frac{f'(x)}{f(x)} = \frac{2}{x( 1 + 2x)} - \frac{1}{x²} ln( 1 + 2x) - cot(x) \\ \)
c ) The derivative of function, f(x) is
\(f'(x) = \frac{( 1 + 2x)^{\frac{1}{x}}}{ sin(x)}( \frac{2}{x( 1 + 2x)} - \frac{1}{x²} ln( 1 + 2x) - cot(x)) \\ \)
A logarithmic differentiation calculator is one of online tool used to calculate the derivative of a function using logarithm.
We have a function, \(f(x) = \frac{( 1 + 2x)^{\frac{1}{x}}}{ sin(x)}\).
We have to use logarithmic differentiation to determine the derivative and other values of the function.
a) Taking natural logarithm both sides in f(x), \(ln (f(x)) = ln( \frac{( 1 + 2x)^{\frac{1}{2}}}{ sin(x)})\)
Now, using the logarithm property,
\(ln(\frac{m}{n}) = ln(m) - ln(n) \)
\(ln (f(x)) = ln( 1 + 2x)^{\frac{1}{x}} - ln(sin(x)) \\ \). Also use power property, ln(p)² = 2ln(p),
\( ln (f(x)) = \frac{1}{x} ln( 1 + 2x) - ln(sin(x)) - - (1) \\ \)
b) Now, we determine the ratio of f'(x)/f(x)
Take a derivative of equation (1), we have
\(\frac{f'(x)}{f (x) } = \frac{2}{x( 1 + 2x)} - \frac{1}{x²} ln( 1 + 2x) - \frac{cos(x)}{sin(x)}\\ \)
\(= \frac{2}{x( 1 + 2x)} - \frac{1}{x²} ln( 1 + 2x) - cot(x) \\ \)
c) Now, we determine the derivative of f(x), Substitute original value of f(x) in previous equation,\( \frac{f'(x)}{ \frac{( 1 + 2x)^{\frac{1}{x}}}{ sin(x)}} = \frac{2}{x( 1 + 2x)} - \frac{1}{x²} ln( 1 + 2x) - cot(x) \\ \)
f'(x) \( = \frac{( 1 + 2x)^{\frac{1}{x}}}{ sin(x)}( \frac{2}{x( 1 + 2x)} - \frac{1}{x²} ln( 1 + 2x) - cot(x)) \\ \). Hence, required value is \( \frac{( 1 + 2x)^{\frac{1}{x}}}{ sin(x)}[ \frac{2}{x( 1 + 2x)} - \frac{1}{x²} ln( 1 + 2x) - cot(x)] \\ \).
For more information about logarithm differentiation , visit:
https://brainly.com/question/30881276
#SPJ4
Which graph below shows the solutions for the linear inequality v2-3x+1?
A
B
10, 1)
(0.1)
с
D
10.1)
16,-1)
16,-1)

Answers
Answer:
A. Graph D
Step-by-step explanation:
y >= -1/3x + 1
this means all the y values that are bigger (= above) than the line definition.
and because it says ">=", the line is included.
If you have a logical statement in four variables how many rows do you need in the truth table that you would use to evaluate it? Answer with a whole number. p → (q→ r) is logically equivalent to (p —— q) → r. True or false? True False If the negation operator in propositional logic distributes over the conjunction and disjunction operators of propositional logic then DeMorgan's laws are invalid. True False
Answers
The number of rows required in a truth table to evaluate a logical statement with four variables is 16. The logical equivalence between "p → (q→ r)" and "(p —— q) → r" is True.
The statement that DeMorgan's laws are invalid if the negation operator distributes over conjunction and disjunction operators is False.
A truth table is a useful tool to evaluate the truth values of logical statements for different combinations of variables. In this case, since there are four variables involved, we need to consider all possible combinations of truth values for these variables.
Since each variable can take two possible values (True or False), we have 2^4 = 16 possible combinations. Therefore, we require 16 rows in the truth table to evaluate the logical statement.
Moving on to the logical equivalence between "p → (q→ r)" and "(p —— q) → r", we can determine if they are equivalent by constructing a truth table. Both expressions have three variables (p, q, and r). By evaluating the truth values for all possible combinations of these variables, we can observe that the truth values of the two expressions are identical in all cases.
Hence, the logical equivalence between "p → (q→ r)" and "(p —— q) → r" is True.
Regarding the statement about DeMorgan's laws, it states that if the negation operator distributes over the conjunction and disjunction operators in propositional logic, then DeMorgan's laws are invalid. However, this statement is false.
DeMorgan's laws state that the negation of a conjunction (AND) or disjunction (OR) is equivalent to the disjunction (OR) or conjunction (AND), respectively, of the negations of the individual propositions. These laws hold true irrespective of whether the negation operator distributes over the conjunction and disjunction operators.
Therefore, the statement about DeMorgan's laws being invalid in such cases is false.
Learn more about DeMorgan's laws
brainly.com/question/32622763
#SPJ11
What is the slope intercept form of (-5,5) & (4,-1)? Need to find the slope, put into point slope form, and then slope intercept. Please explain how to solve it. Need help ASAP.
Answers
The text is asking for the slope-intercept form of a linear equation that passes through two given points, (-5,5) and (4,-1). The slope-intercept form of a linear equation is y = mx + b, where m is the slope and b is the y-intercept. To find the slope, we use the formula: m = (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are the given points. Once we find the slope, we can use it to write the equation in point-slope form: y - y1 = m(x - x1). Finally, we can rearrange the point-slope form to get the slope-intercept form.
PEASE MARK BRAINLIEST
determine whether the random variable x is discrete or continuous. explain. let x represent the amount of rain that fell in spring
Answers
The random variable x, which represents the amount of rain (in inches) that fell this spring, is a continuous random variable.
In this context, a continuous random variable is one that can take on any value within a certain range. The amount of rain can be measured with different levels of precision, such as 2.5 inches or 2.5342 inches, indicating that there is an infinite number of possible values between any two given points.
On the other hand, a discrete random variable would involve countable outcomes or a finite number of possible values. For example, if we were counting the number of rainy days during the spring, the random variable would be discrete since it can only take whole number values.
In the case of measuring the amount of rain, there can be infinitely many possible values within any given range, and therefore, it is considered a continuous random variable. So, the correct answer is option A.
Learn more about variable here:
https://brainly.com/question/28248724
#SPJ11
The complete question is:
Decide whether the random variable x is discrete or continuous. Explain your reasoning Let x represent the amount of rain (in inches) that fell this spring. Is the random variable x discrete or continuous? Choose the correct answer below.
A. Continuous, because x is a random variable that cannot be counted.
B. Discrete, because x is a random variable that can be counted.
pls pls pls pls help me istg ill be your best friend and give you brianliest and all the points i can give and ill love you forvever pls pls pls pls

Answers
a. The chart did not maintain consistent scaling
b. The graph is not the appropriate graph type to display such data
c. The display had inaccurate or distorted visual representations
How do we explain?When the actual data may not support it, changing the scales on the axes might give the appearance of big changes or differences.
The visual effect of data can be exaggerated or minimized, for instance, by adopting a non-linear scale or deleting specific sections of the axis.
So it important to Choose appropriate graph type that best represents the data and the relationship you want to convey.
It also advisable to make use of clear and accurate labeling with descriptive titles and units of measurement.
Learn more about graphs at:
https://brainly.com/question/19040584
#SPJ1
Simplify the expression where possible. (6 3 ) -3
Answers
which expression is a possible leading term for the polynomial function graphed below? –18x14 –10x7 17x12 22x9
Answers
Among the given expressions, the one that could be the possible leading term for the polynomial function graphed below is -18x¹⁴.
The leading term of a polynomial function is the term containing the highest power of the variable. Among the given expressions, the one that could be the possible leading term for the polynomial function graphed below is -18x¹⁴.
The degree of a polynomial function is the highest degree of any of its terms.
If a polynomial has only one term, then the degree of that term is the degree of the polynomial and is also called a monomial.
For example, consider the given function:Now, observe the degree of the function, which is 14, as the highest exponent of the function is 14.
Thus, the term containing the highest power of the variable x is -18x¹⁴.
Therefore, among the given expressions, the one that could be the possible leading term for the polynomial function graphed below is -18x¹⁴.
To know more about probability visit :-
https://brainly.com/question/1496352
#SPJ11
Find the distance between the pair of points.
(6, 6) and (6, −2)
The distance between the pair of points is units.
Answers
Answer:
(6-6)+(6-2)=0+4
sqr(4)^2=4
the numbers 1447, 1005, and 1231 have something in common: each is a 4-digit number beginning with 1 that has exactly two identical digits. how many such numbers are there?
Answers
There can be 432 Types of Combinations for a 4-digit number beginning with 1 that has exactly two identical digits
What is permutation and combination?
The process of placing all the components of a set into a certain sequence or order is known as permutation in mathematics. In other terms, the process of permuting is the reordering of the components of a set if the set is already ordered. Nearly all areas of mathematics involve permutations in some form or another. They frequently appear when various orderings on particular finite sets are taken into account.The combination is a way of selecting items from a collection, such that (unlike permutations) the order of selection does not matter. In smaller cases, it is possible to count the number of combinations. Combination refers to the combination of n things taken k at a time without repetition. To refer to combinations in which repetition is allowed, the terms k-selection or k-combination with repetition are often used.\($11xy,\qquad 1x1y,\qquad1xy1$\)
Because the number must have exactly two identical number digits,\($x\neq y$\), \($x\neq1$, and $y\neq1$\). Hence, there are \($3\cdot9\cdot8=216$\) number of this form.
Now suppose that the two identical digits are not 1. Reasoning similarly to before, we have the following possible combination:
\($1xxy,\qquad1xyx,\qquad1yxx.$\)
Again,,\($x\neq y$\), \($x\neq1$, and $y\neq1$\). There are \($3\cdot9\cdot8=216$\) numbers of this form.
Thus the answer is 216+216=432
Learn more about permutation and combination from the links below
https://brainly.com/question/13387529
https://brainly.com/question/10164077
#SPJ4
the number is 869214.951 , i need the answers for fractions and decimals and power of 10.

Answers
Answer:
Step-by-step explanation:
Fraction:
\(869214.951=\dfrac{869214951}{1000}\\\)
Power of 10:
\(869214.951=8.69214951 * 10^{5}\)
At the instant shown, the shaft and plate rotates with an angular velocity of 19 rad/s and angular acceleration of 9 rad/s2 0.6 m 0.2 m 0.4m 0.3 m 0.3 m 0.4 m Part A eterminethe wocl a n D sea c Enter the ", y, and Z components of the velocity separated by commas vec m/s Submit Request Answer Part B Determine the acceleration of point D located on the corner of the plate at this instant. Enter the , y, and Z components of the velocity separated by commas vec m/s Submit Request Answer
Answers
The acceleration components of point D are, ax = 3.6 m/s², ay = 6.4 m/s², az = -1.14 m/s²
At the instant shown, the shaft and plate rotates with an angular velocity of 19 rad/s and angular acceleration of 9 rad/s2. The given diagram is shown below. Angular velocity (w) = 19 rad/sAngular acceleration (α) = 9 rad/s²Plate dimension AB = 0.6 m, BC = 0.2 m, CD = 0.4 m, DA = 0.3 m, AE = 0.3 m and EF = 0.4 m.
Determine the wocl and Dsea of Enter the ", y, and Z components of the velocity separated by commas vec m/sThe velocity components for point D can be calculated using the following formula.Vd = R x wWhere R is the position vector of D relative to the origin.
According to the given diagram, the position vector of point D relative to the origin is, R = 0.2i + 0.4j + 0.3kThe velocity of point D can be calculated as follows.Vd = R x w = 0.2i + 0.4j + 0.3k x 19The cross product of R and w can be calculated as follows.i j k 0.2 0.4 0.3 0 19 0 = [(0.4 × 0) - (0.3 × 19)] i - [(0.2 × 0) - (0.3 × 0)] j + [(0.2 × 19) - (0.4 × 0)] kVd = -5.7i + 6.8kThus, the velocity components of point D are, Vx = -5.7 m/s, Vy = 0 m/s, Vz = 6.8 m/s
Determine the acceleration of point D located on the corner of the plate at this instant. Enter the, y, and Z components of the velocity separated by commas vec m/sThe acceleration components of point D can be calculated using the following formula.aD = R x α + w x (w x R)Where R is the position vector of D relative to the origin.
According to the given diagram, the position vector of point D relative to the origin is, R = 0.2i + 0.4j + 0.3kThe acceleration of point D can be calculated as follows.aD = R x α + w x (w x R) = (0.2i + 0.4j + 0.3k) x 9 + 19 x (19 x (0.2i + 0.4j + 0.3k)) = (0.4k - 0.3j) x 9 + 19 x (0.4 x (0.4j - 0.3k))aD = 3.6i + 6.4j - 1.14k.
Learn more about Acceleration
brainly.com/question/12550364
#SPJ11
A sample of 25 observations has been represented by a model of the form y = β0 + β1x1 + β2x2 + ϵ, where ϵ is a random error term with mean 0 and variance σ 2 . You are given: (X′X) −1 = 188.9832 0.8578 −28.0275 0.8578 0.2500 −0.6000 −28.0275 −0.6000 5.0625 s 2 = 0.0361 βˆ = −4.04 0.14 0.45 Determine the shortest symmetric 95-percent confidence interval for β1
Answers
The shortest symmetric 95% confidence interval for β1 is approximately (-0.0018, 0.2818) based on the given information, using the formula CI = βˆ1 ± 2.069 * sqrt(0.0361 * 0.25).
To determine the shortest symmetric 95% confidence interval for β1, we can use the formula:
CI = βˆ1 ± t_(n−p,α/2) * SE(βˆ1)
Where:
- CI represents the confidence interval, - βˆ1 is the estimated coefficient for x1 (0.14 in this case), - t_(n−p,α/2) is the critical t-value with n-p degrees of freedom and α/2 significance level, - SE(βˆ1) is the standard error of the estimated coefficient for x1
Given that you have not provided the values of n (number of observations) and p (number of predictors), I'll assume that n = 25 (as mentioned in the sample) and p = 2 (since there are two predictor variables: x1 and x2).
The critical t-value can be calculated using the inverse of the t-distribution function. Since we want a 95% confidence interval (α = 0.05) and the distribution is symmetric, α/2 equals 0.025.
Now let's calculate the confidence interval:
SE(βˆ1) = sqrt(s^2 * [(X'X)^-1]_22)
where [(X'X)^-1]_22 is the second element of the second row of (X'X)^-1
SE(βˆ1) = sqrt(0.0361 * 0.25)
Next, we need to calculate the critical t-value, t_(n−p,α/2), with n-p degrees of freedom. Using a t-distribution table or a statistical software, we find that t_(23,0.025) ≈ 2.069.
Now we can calculate the confidence interval:
CI = 0.14 ± 2.069 * sqrt(0.0361 * 0.25)
Finally, we can compute the confidence interval:
CI = 0.14 ± 2.069 * 0.0675
CI ≈ 0.14 ± 0.1398
The shortest symmetric 95% confidence interval for β1 is approximately (-0.0018, 0.2818).
To learn more about symmetric click here brainly.com/question/30697892
#SPJ11
Find a value of c so that P(Z ? c) = 0.71. a) -1.11 b) 0.75 c) -0.55 d) 0.55 e) 1.55
Answers
Among the provided answer options, the closest value to -0.555 is -0.55, which is option c. Therefore, option c (-0.55) is the value of c that satisfies P(Z ? c) = 0.71.
The notation P(Z ? c) represents the probability that a standard normal random variable Z is less than or equal to c. To find the value of c that corresponds to P(Z ? c) = 0.71, we need to determine the Z-score associated with this probability.
Using a standard normal distribution table or a calculator, we can find that a Z-score of approximately 0.555 corresponds to a cumulative probability of 0.71. However, since we are looking for the value of c in P(Z ? c), we need to consider the opposite inequality.
Learn more about probability here:
https://brainly.com/question/14210034
#SPJ11
brainliest for correct answer

Answers
Answer:
5
Step-by-step explanation:
The difference between the park and house of a student is 1Km 575m. Every day he walks both ways between the park and his house. Find the total distance covered by him in a week's time?
Answers
The student covers a total distance of 22.05 kilometers in a week's time, walking between the park and the house each day.
To find the total distance covered by the student in a week's time, we need to calculate the distance covered in one round trip (from the house to the park and back) and then multiply it by the number of round trips in a week.
Given that the difference between the park and house is 1 kilometer and 575 meters, we can convert it to a total distance of 1.575 kilometers.
In a round trip, the student covers twice the distance between the park and the house, which is 1.575 kilometers * 2 = 3.15 kilometers.
Now, we need to determine how many round trips the student makes in a week. Let's assume the student makes one round trip each day.
Since there are 7 days in a week, the total distance covered by the student in a week's time is 3.15 kilometers * 7 = 22.05 kilometers.
for similar questions on distance.
https://brainly.com/question/26046491
#SPJ8
3. If the average of 16, 14, x, 23, 20 is 18, find the value of x.
LA
Maths
Answers
Answer:
x = 17
Step-by-step explanation:
Here, we want to find the value of x
mathematically, the mean is the sum of the numbers divided by the count of the numbers
The count of the numbers is 5
So we have;
(16 + 14 + x + 23 + 20)/5 = 18
73 + x = 5(18)
73 + x = 90
x = 90-73
x = 17
WILL GIVE BRAINLESS IF YOU GOT IT CORRECT
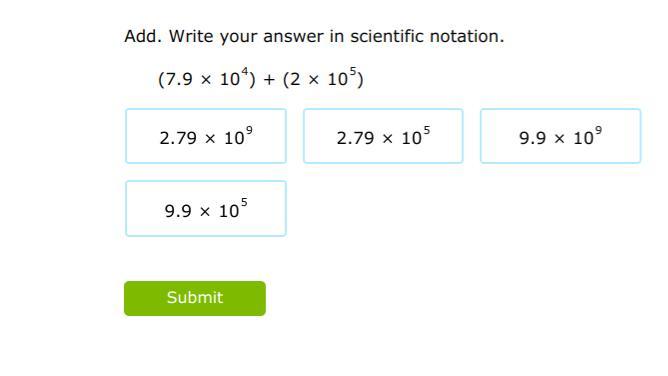
Answers
Answer: 2.79 x 10 to the 5th power
Step-by-step explanation: Your welcome :)
Answer:
2.79 x \(10^{5} }\)
Step-by-step explanation:
7.9 x \(10^{4}\) = 79000
2 x \(10^{5}\) = 200000
79000 + 200000 = 279000
279000 = 2.79 x \(10^{5} }\)
Hope this helps, I'm sorry about the earlier question but I fixed it:)
Find the inverse of each function. Is the inverse a function?
f(x)= √2 x-1+3
Answers
Yes , the given function is an inverse function which is given by \(f^{-1}(y)=\frac{y-2}{\sqrt{2} }\) .
An inverse function or anti -function is defined as a function that can be inverted into another function. Simply put, if the function 'f' makes x into y, the inverse of 'f' makes y into x. Where a function is denoted by 'f' or 'F', the inverse is denoted by f-1 or F-1. A function accepts values, performs some operation on those values, and produces an output. The inverse function works in line with the result and returns to the original function. An inverse function returns the original value that the function provided the output for.
We have given a function \(f(x)=x\sqrt{2} -1+3\) . ....(1)
On simplifying the equation we, get
\(f(x)=x\sqrt{2} +2\)
Let y = f(x)
\(y=x\sqrt{2} +2\\\\y-2=x\sqrt{2}\\\\x=\frac{y-2}{\sqrt{2} }\) ......(2)
Swap the values of x and y, then the inverse is then
\(x=f^{-1}(y)\) ...(3)
Comparing equation (2) and (3) , we get
\(f^{-1}(y)=\frac{y-2}{\sqrt{2} }\)
We can check that this is really an inverse function or not
Putting \(x=f^{-1}\) in equation (1) , we get
\(f(f^{-1}(y))=\frac{y-2}{\sqrt{2} } \sqrt{2} -1+3\\\\y=y-2+2\\\\y=y\)
As LHS = RHS which means inverse function is correct .
Learn more about inverse function here :
https://brainly.com/question/14391067
#SPJ4
Help, I am very confused

Answers
9514 1404 393
Answer:
(a) 2S, 1A
Step-by-step explanation:
A triangle is completely specified when all three sides and all three angles are known. This triangle shows the measure of 1 side, so 2 sides are missing (2S). It shows the measures of angle Q and P, so angle N is missing (1A).
The missing information is 2 sides and 1 angle: 2S, 1A.

jill has 15 feet ribbion how many yards ribbon does she have
Answers
Answer:
Step-by-step explanation
You would take 15 ft and divide it by how many feet are in a yard which is 3.
Answer - Jill has 5 yards of ribbon
Answer:
5 yards
Step-by-step explanation:
every 3 feet are 1 yard... 15 feet divided by the 3 = 5 yards
determine whether the following are linear trans- formations from r2 into r3.
(a) L(x) = (x1, L2, 1)^T
(b) L(x) = x1,0,0)^t
Answers
(a) The transformation L(x) = (x1, L2, 1)^T is not a linear transformation from ℝ² to ℝ³. In order for a transformation to be linear, it must satisfy two conditions: preservation of addition and preservation of scalar multiplication.
For preservation of addition, we need L(u + v) = L(u) + L(v) for any vectors u and v in ℝ². However, in this case, if we consider two vectors u = (u₁, u₂) and v = (v₁, v₂), the transformation L(u + v) would be (u₁ + v₁, L2, 1)^T, while L(u) + L(v) would be (u₁, L2, 1)^T + (v₁, L2, 1)^T = (u₁ + v₁, 2L2, 2)^T. Since 2L2 ≠ L2 and 2 ≠ 1, we can see that the preservation of addition condition is not satisfied.
Therefore, the transformation L(x) = (x1, L2, 1)^T is not a linear transformation.
(b) The transformation L(x) = (x₁, 0, 0)^T is a linear transformation from ℝ² to ℝ³. This transformation simply takes the x-coordinate of a vector in ℝ² and maps it to the x-coordinate of a vector in ℝ³, while setting the y and z coordinates to zero.
To verify the linearity of this transformation, we need to check the preservation of addition and preservation of scalar multiplication conditions. For any vectors u = (u₁, u₂) and v = (v₁, v₂) in ℝ², we have:
L(u + v) = (u₁ + v₁, 0, 0)^T = (u₁, 0, 0)^T + (v₁, 0, 0)^T = L(u) + L(v),
which shows the preservation of addition. Similarly, for any scalar c and vector u = (u₁, u₂) in ℝ², we have:
L(cu) = (cu₁, 0, 0)^T = c(u₁, 0, 0)^T = cL(u),
which demonstrates the preservation of scalar multiplication.
Therefore, the transformation L(x) = (x₁, 0, 0)^T is a linear transformation from ℝ² to ℝ³.
To learn more about linear transformation; -brainly.com/question/13595405
#SPJ11
Aiden models a can of ground coffee as a right cylinder. He measures its radius as
in and its volume as 12 cubic inches. Find the height of the can in inches. Round your
answer to the nearest tenth if necessary.
Answers
To find the height of the can, we need to use the formula for the volume of a cylinder, which is V = πr^2h, where V is the volume, r is the radius, and h is the height.
We know that the radius is in inches and the volume is 12 cubic inches, so we can substitute these values into the formula and solve for h.
First, we need to find the value of the radius, which is given as "in". It is likely that the radius was measured in inches, so we will assume that "in" means inches. Therefore, the radius is r = in = 1 inch.
Now we can substitute the values into the formula and solve for h:
12 = π(1^2)h
h = 12/(π)
h ≈ 3.8 inches (rounded to the nearest tenth)
Therefore, the height of the can of ground coffee is approximately 3.8 inches.
To learn more about volume of a cylinder, click here:
brainly.com/question/15891031
#SPJ11
HELP ME PLS I NEED HELP RN

Answers
Answer:
Step-by-step explanation:
I gotchu.
sin70 = x/3.6
x = 3.6sin70
x = 3.4
Answer:
x = 3.4
Step-by-step explanation:
As the given triangle is a right triangle we can use trigonometric ratios to solve for x.
\(\boxed{\begin{minipage}{9.4 cm}\underline{Trigonometric ratios} \\\\$\sf \sin(\theta)=\dfrac{O}{H}\quad\cos(\theta)=\dfrac{A}{H}\quad\tan(\theta)=\dfrac{O}{A}$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}\)
From inspection of the triangle:
θ = 70°O = AB = xA = BCH = AC = 3.6As we know the angle and the hypotenuse, and wish to find the side opposite the angle, substitute the values into the sine ratio and solve for x:
\(\implies \sin(70^{\circ})=\dfrac{x}{3.6}\)
\(\implies x=3.6\sin(70^{\circ})\)
\(\implies x=3.382893...\)
\(\implies x=3.4\; \sf (nearest\;tenth)\)
Therefore, x = 3.4 to the nearest tenth.
find the volume of a cylinder with a height of 7 cm and a radius of 3 cm ?

Answers
B
Step-by-step explanation:
Talha had $150. He spent 35% of his money on clothes and 15% on Perfumes. How much money did he spend on the two items?
$60
$75
$50
$85
Answers
Answer:
$75
Step-by-step explanation:
150 x 0.35 = 52.50
150 x 0.15 = 22.50
(or do 50% of whole total)
22.50 +52.50 = $75
Answer:
75
Step-by-step explanation:
since he spent a total of 50% of his money (35%+15%), then 50% of 150 is 75
Find the general solution of the given differential equation, and use it to determine how solutions behave as t approaches infinity.
1. y'-2y+3e^t
2. 2y'+y=3t
3. ty'-y=t^2e^t t>0
For 1 and 2 I've been able to get to the part where you solve for p(t) and u(t) ie. #1: p(t)=-2 u(t)=e^2t but I'm a little confused what to do/ how to get d/dt(u*y)=....
Please show all work! Thanks
Answers
The general solution to the differential equation y' - 2y + 3e^t = 0 is: y = Ce^(2t) - e^t. As t approaches infinity, the solution approaches infinity because the dominant term in the solution is e^(2t).
The given differential equation is:
y' - 2y + 3e^t = 0
We can first find the homogeneous solution by setting the right-hand side equal to zero:
y' - 2y = 0
This is a separable differential equation that can be solved by separating variables:
dy/y = 2dt
Integrating both sides, we get:
ln|y| = 2t + C
where C is an arbitrary constant. Solving for y, we get:
y = Ce^(2t)
This is the general solution to the homogeneous equation.
Now, we need to find a particular solution to the non-homogeneous equation. Since the non-homogeneous term is a constant times e^t, we can guess a particular solution of the form:
y_p = Ae^t
where A is a constant. Substituting this into the original equation, we get:
Ae^t - 2Ae^t + 3e^t = 0
Simplifying, we get:
A = -1
Therefore, the particular solution is:
y_p = -e^t
The general solution to the non-homogeneous equation is the sum of the homogeneous solution and the particular solution:
y = Ce^(2t) - e^t
To determine how solutions behave as t approaches infinity, we can analyze the behavior of the exponential terms. Since e^(2t) grows much faster than e^t, the dominant term as t approaches infinity is e^(2t). Therefore, the solution approaches infinity as t approaches infinity.
Learn more about differential equation here
brainly.com/question/30624850
#SPJ4
Convert s to ms
i. 6x 10¹ s
Answers
The conversion of the given equation 6x 10¹ s = 60000ms.
How does time become converted?To convert time to hours, divide it by 24, the number of hours in a day. When converting time onto minutes, multiply it by 1440 (the number of minutes in a day, 24*60). To convert time to seconds, multiply it by 86400 (the number of seconds in a day) (24*60*60).
Given:6x 10¹ s
This can be written as:
60 s
To Calculate Seconds To Milliseconds
Simply increase your seconds by 1000 to convert seconds to milliseconds. This is the formula:
Yms = Xs * 1000
We know that:
1s = 1000ms
So,
60s = 1000 * 60
= 60000ms.
To Calculate Seconds To Milliseconds
To know more about unit convert visit:
https://brainly.com/question/27971860
#SPJ9