What is the goal of a proof by contradicción?
Answers
Answer:
In logic and mathematics, proof by contradiction is a form of proof that establishes the truth or the validity of a proposition, by showing that assuming the proposition to be false leads to a contradiction.
Step-by-step explanation:
Related Questions
solve for x using Logarithm
4^x+6^x =9^x
Answers
4^x + 6^x - 9^x = 0
2^2x + (2×3)^x - 3^2x = 0
2^2x + 2^x×3^x - 3^2x = 0
(⅔)^2x + (⅔)^x - 1 = 0
let t = ( ⅔)^x
t² + t - 1 = 0
t = (-1+√5 ) / 2
(⅔)^x = (-1+√5 ) / 2
x = Log base ⅔ ((-1+√5 ) / 2 )
x = 1.18681
For the equation f(x) = 1.1 * (0.44) ^ x state the initial value C, the growth or decay factor a, and percent change R for each unit increase in x
c = (Type an integer or a decimal)
a = (Type an integer or a decimal)
R = % (Simplify your answer. Type an integer or a decimal)
Answers
The parameters of the exponential function in this problem are given as follows:
c = 1.1.a = 0.56.R = -56%.What is an exponential function?The standard format of an exponential function is given as follows:
y = c(1 - a)^t.
This is the case for a decaying exponential function, and the meaning of each parameter is given as follows:
c is the initial value, value assumed by y when t = 0.a is the decay rate.In this problem, the function is given as follows:
f(x) = 1.1(0.44)^x.
Hence the values for the parameters are given as follows:
c = 1.1, which is the initial value.a = 0.56, as 1 - a = 0.44 -> a = 0.56.Then the percent of change is of -56%, as it is a decaying exponential function with a = 0.56.
More can be learned about exponential functions at https://brainly.com/question/25537936
#SPJ1
An FICA tax of 7.51% and an SDI deduction of 1.2% are charged against
an employee's wages. If her total monthly wages were $1538.46, what
would her paycheck be after FICA and SDI deductions as well as
withholding tax deductions of $245.80?
Answers
The employee's paycheck after FICA and SDI deductions as well as
withholding tax deductions is $1158.65.
What is FICA?FICA is a federal payroll tax in the US. It is taken out of every paycheck and stands for the Federal Insurance Contributions Act. Your nine-digit number enables Social Security to precisely record your self-employment or insured wages. You accrue credits for Social Security benefits as you work and pay FICA taxes.
Employee monthly salary= $1538.46FICA calculation= 7.51% of $1538.46= $115.54SDI calculation= 1.2% of $1538.46= $18.47Employee final paycheck= Monthly wage - FICA - SDI - Tax deductions.$1538.46 - $115.54 - $18.47 - $245.80= $1158.65The final monthly paycheck of the employee after deducting all taxes is $1158.65.
To learn more about FICA, refer to,
https://brainly.com/question/24049080
#SPJ13
the question is 4 1/5 x 5/14
Answers
Answer:
3/2
Step-by-step explanation:
Simplify the following:
((4 + 1/5)×5)/14
((4 + 1/5)×5)/14 = ((4 + 1/5)×5)/14:
((4 + 1/5)×5)/14
Put 4 + 1/5 over the common denominator 5. 4 + 1/5 = (5×4)/5 + 1/5:
(((5×4)/5 + 1/5) 5)/14
5×4 = 20:
((20/5 + 1/5)×5)/14
20/5 + 1/5 = (20 + 1)/5:
(((20 + 1)/5)×5)/14
20 + 1 = 21:
(21/5×5)/14
21/5×5 = (21×5)/5:
((21×5)/5)/14
((21×5)/5)/14 = (21×5)/(5×14):
(21×5)/(5×14)
(21×5)/(5×14) = 5/5×21/14 = 21/14:
21/14
The gcd of 21 and 14 is 7, so 21/14 = (7×3)/(7×2) = 7/7×3/2 = 3/2:
Answer: 3/2
the function (f *g) (x) is found by replacing each occurrence of x in the equation for f(f) with
Answers
Using the concept composite function, we have that:
The function \((f \circ g)(x)\) is found replacing each occurrence of x in the equation f(x) with the output of function g(x) for the respective value of x.
--------------------------------------
The composite function of f and g of x is given by:
\((f \circ g)(x) = f(g(x))\)
That is, the input of the function f for a given value of x is the output of function g for this given value of x.
Thus, the sentence is completed as:
The function \((f \circ g)(x)\) is found replacing each occurrence of x in the equation f(x) with the output of function g(x) for the respective value of x.
A similar problem is given at https://brainly.com/question/23458455
4. Sketch the graph of F(x) = 1 +x/x²-1
Answers
The graph of the function is attached below.
What is the graph of a function?The graph of a function shows the correlation between its inputs (represented by x-values) and matching outputs (represented by y-values). It is a means of illustrating the actions and traits of a function.
Plotting points that conform to the function's rule in a cartesian coordinate system results in the graph of the function. An input-output pair for the function is represented by each point on the graph. The point's x-coordinate represents the input value, while its y-coordinate represents the output value.
We can further use the graph to determine the range, domain, y-intercept, x-intercept and so many others from a graph.
In the given problem;
The graph of the function f(x) = 1 + x / x² - 1 is attached below;
Learn more on graph of a function here;
https://brainly.com/question/7807573
#SPJ1

5. A certain company stock began at a starting price of $23
per share. After five weeks of trading, the new company
stock has changed price every week, x, according to the
function h(x) = 25(0.93)*.
Which of the following is true?
F. The stock has increased by 93% of its original value.
G. The stock has lost 79% of its value every week.
H. The stock is worth $23.25 per share after five weeks.
). The stock has more than doubled its original value.
Answers
Answer:
$ 56.25 is he answer
Step-by-step explanation:
.... .. . . . . . . ............ ......
Suppose a regular n-gon is inscribed in a circle of radius r. Diagrams are shown for n=6, n=8, and n = 12. n = 6 n=8 n = 12 a a VT a Imagine how the relationship between the n-gon and the circle changes as n increases. 1. Describe the relationship between the area of the n-gon and the area of the circle as n increases.
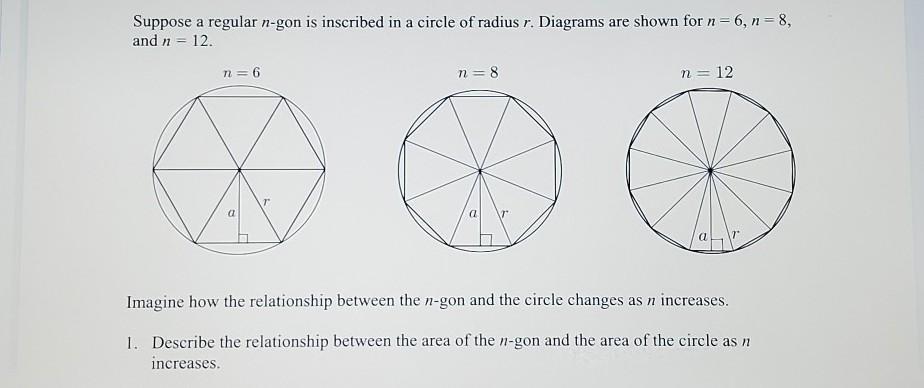
Answers
Answer:If an N-gon (polygon with N sides) has perimeter P, then each of the
N sides has length P/N. If we connect two adjacent vertices to the
center, the angle between these two lines is 360/N degrees, or 2*pi/N
radians. (Do you understand radian measure well enough to follow me
this far?)
The two lines I just drew, plus the side of the polygon between them,
form an isosceles triangle. Adding the altitude of the isosceles
triangle makes two right triangles, and we can use one of them to
derive the equation
sin(theta/2) = s/(2R)
where theta is the apex angle (which I said is 2*pi/N radians), R is
the length of the lines to the center (the radius of the circumscribed
circle), and s is the length of the side (which I said is P/N).
Putting those values into the equation, we have
sin(pi/N) = P/(2NR)
so that
P = 2NR sin(pi/N)
gives the perimeter of the N-gon with circumradius R.
Can we see a connection between this formula and the perimeter of a
circle? The perimeter of the circumcircle is 2*pi*R. As we increase
N, the perimeter of the polygon should get closer and closer to this
value. Comparing the two, we see
2NR*sin(pi/N) approaches 2*pi*R
N*sin(pi/N) approaches pi
You can check this out with a calculator, using big numbers for N such
as your teacher's N=1000. If you calculate the sine of an angle in
degrees rather than radians, the formula will look like
N*sin(180/N) --> pi
Step-by-step explanation:
An 8-sided number cube is rolled 4000 times. The number 2 appeared 200 times. Determine the theoretical and experimental probability of rolling a 2 in order to determine the fairness of the number cube. Drag values or words to the boxes to correctly complete the statements.
Answers
Theoretical Probability of rolling a 2= 1/20
Experimental Probability of rolling a 2 = 1/20
Theoretical probability of rolling a 2:
The theoretical probability of an event is the ratio of the number of favourable outcomes to the total number of possible outcomes. Since there are 8 sides to the cube, the total number of possible outcomes is 8. Since the number 2 appeared 200 times out of 4000 rolls, the number of favorable outcomes is 200. Therefore, the theoretical probability of rolling a 2 is:
Theoretical Probability of rolling a 2 = Number of favourable outcomes / Total number of possible outcomes = 200/4000 = 1/20
Experimental probability of rolling a 2:
The experimental probability of an event is the ratio of the number of times the event occurred to the total number of trials. In this case, the event is rolling a 2, which occurred 200 times out of 4000 rolls.
Therefore, the experimental probability of rolling a 2 is:
Experimental Probability of rolling a 2 = Number of times the event occurred / Total number of trials = 200/4000 = 1/20
Comparing theoretical and experimental probability:
If the cube is fair, we would expect the theoretical probability and the experimental probability to be similar. In this case, both probabilities are 1/20, which means that the cube appears to be fair. However, we would need to conduct more trials to be more confident in our conclusion.
For such more questions on Probability
https://brainly.com/question/251701
#SPJ8
2/5 of employees in a company drive to work, 1/3 travel by bus and the rest walk. 1. Find the fraction of who walk.
Answers
Answer:
4/15
Step-by-step explanation:
2/5 drive
1/3 bus
and rest walk
fraction of those who walk is 1-(2/5+1/3)
2/5+1/3=(6+5)/15=11/15
15/15-11/15=4/15
What is the product of 2 linear functions?
Answers
The product of two linear functions having same variables will be a quadratic function where as the The product of two linear functions having different variables will be a linear function.
Linear function is the function whose degree is 1.
Degree of a function is the highest power of the variable of the function.
Let us take two examples.
1. Suppose the two linear functions are -
f(x) = 2x + 3 and g (x) = x + 5
The product of f(x) and g(x) will be
(2x + 3)(x + 5)
=2x (x + 5) + 3 (x + 5)
= 2x² + 10x + 3x + 15
= 2x² + 13x + 15
Here, f(x) and g(x) are the functions having same variables so there product is a quadratic function.
2. Suppose the two linear functions are -
f(x) = 2x + 3 and g (y) = y + 5
The product of f(x) and g(y) will be
(2x + 3)(y + 5)
=2x (y + 5) + 3 (y + 5)
= 2xy + 10x + 3y + 15
Here, f(x) and g(y) are the functions having different variables so there product is a linear function.
To know more about quadratic function here. https://brainly.com/question/27958964#
#SPJ4
Solve this inequality:
-12a +7<31
Answers
Answer:
a > -2
Step-by-step explanation:
-12a +7<31
Subtract 7 from each side
-12a +7-7<31-7
-12a <24
Divide by -12, remembering to flip the inequality
-12a/-12 >24/-12
a > -2
Answer:
a>-2
Step-by-step explanation:
\(\sf{}\)
=> -12a +7 <31
=> -12a+7-7<31-7
=> -12a<24
=> a>-2
If a = 12 and 120% of a is equal to 80\% of bthen what is a + b ?
Answers
Answer:
The answer is 30
Step-by-step explanation:
First you have to find 120% of a (12).
\( \frac{12}{1} \times \frac{120}{100} = 14.4\)
Therefore; 14.4 is 80% of b, and we are trying to find 100% of b
\(14.4 = 80\% \\ x = 100\%\)
we do not know what is 100% therefore we call it *x*. In order to find this unknown value *x* we cross multiply.
\(14.4 \times 100\% = 80\% \times x\)
This is the same as saying;
\(14.4 \times 1 = x \times \frac{4}{5} \)
100% percent would be 1 because it is the whole number we are trying to find. The 80% would be 4/5. To get 4/5 you can simply break down 80/100 ( this is 80% as a fraction).
so the new equation is: 14.4= 4/5x
We divide both sides by 4/5. Then we will get x tobe equal to 18. Therefore b is 18. We were asked to find (a + b) so. 18+12 = 30
A
B
C
is a right-angled triangle.
Calculate the length of
B
C
.
Give your answer correct to 1 decimal place.
Answers
Answer:
b= 60
c=30
Step-by-step explanation:
every triangle is equal to 180°
180°-90=90
b=90-60=30
c=30
cos(x+pi/3)-sin2x=0 ahihihihihihiihihihihihih
Answers
Answer:cos(x+pi/3) - sin2x=0
<=> cos(x+pi/3)=sin2x
<=> cos(x+pi/3)=cos(pi/2-2x)
<=>x+pi/3=pi/2-2x+k2pi
Or x+pi/3=-pi/2 +2x+k2pi
<=>x=pi/18 + k2pi/3
Or x=5pi/6 +k2pi
Step-by-step explanation:
Which best describes the figure
Answers
The best description of the figure would be that it is a C. a square.
How to find the figure type ?To find out the type of figure that we have, it would be best to find the lengths of the sides of the figure. We should find AB, BC, CD, and AD.
We can use the distance formula which is:
D=√ ( x 2 - x1 ) ² + ( y2 - y1) ²
Using this formula, we find that AB, BC, CD, and AD are all a distance of 6 units. This therefore means that this figure is a square because all the sides are equal.
Find out more on figures at https://brainly.com/question/20642848
#SPJ1
Full question is:
Which best describes the figure that is represented by the following coordinates?
A(-3, 4), B(3, 4), C(3,-2) and D(-3,-2)
a rectangle
a trapezoid
a square
Here is a picture of some sea animals. The number line on the left shows the vertical position of each animal above or below sea level, in meters.
1. How far above or below sea level is each animal? Measure to their eye level.
2. A mobula ray is 3 meters above the surface of the ocean. How does its vertical position compare to the
height or depth of:
The jumping dolphin?
The flying seagull?
The octopus?
3. An albatross is 5 meters above the surface of the ocean. How does its vertical position compare to the
height or depth of:
The jumping dolphin?
The flying seagull?
The octopus?
4. A clownfish is 2 meters below the surface of the ocean. How does its vertical position compare to the
height or depth of:
The jumping dolphin?
The flying seagull?
The octopus?
5. The vertical distance of a new dolphin from the dolphin in the picture is 3 meters. What is its distance from the surface of the ocean?

Answers
Answer:
How far above or below sea level is each animal? Measure to their eye level.The jumping dolphin is approx. 6 meters under sea level
The flying seagull is approx. 8 meters under sea level
The mobula ray is approx. 2 meters under sea level
The clownfish is approx.t 4 meters under sea level
The octopus is approx. 8 meters under sea level
A mobula ray is 3 meters above the surface of the ocean. How does its vertical position compare to the height or depth of:The jumping dolphin: The mobula ray is 9 meters lower than the jumping dolphin.
The flying seagull: The mobula ray is 11 meters lower than the flying seagull.
The octopus: The mobula ray is 11 meters higher than the octopus.
An albatross is 5 meters above the surface of the ocean. How does its vertical position compare to the height or depth of:The jumping dolphin: The albatross is 1 meter lower than the jumping dolphin.
The flying seagull: The albatross is 3 meters lower than the flying seagull.
The octopus: The albatross is 13 meters higher than the octopus.
A clownfish is 2 meters below the surface of the ocean. How does its vertical position compare to the height or depth of:The jumping dolphin: The clownfish is 8 meters lower than the jumping dolphin.
The flying seagull: The clownfish is 10 meters lower than the flying seagull.
The octopus: The clownfish is 6 meters higher than the octopus.
The vertical distance of a new dolphin from the dolphin in the picture is 3 meters. What is its distance from the surface of the ocean?If the new dolphin is above the dolphin in the picture, then its distance from the surface of the ocean is 6 - 3 = 3 meters.
If the new dolphin is below the dolphin in the picture, then its distance from the surface of the ocean is 6 + 3 = 9 meters.
✧☆*: .。. Hope this helps, happy learning! (✧×✧) .。.:*☆✧
I hour has 60 minutes true or false
Answers
Answer:
True
Step-by-step explanation:
help me asap. my exam is tomorrow.

Answers
The total surface area of the doghouse is 1452 ft²
What is surface area?The area occupied by a three-dimensional object by its outer surface is called the surface area.
The dog house has many surfaces including the roofs . The total surface area is the sum of all the area of the surfaces.
area of the roof part = 2( 13×11) + 2( 12× 10)×1/2
= 286 + 720
= 1006 ft²
surface area of the building
= 2( lb + lh + bh) -bh
= 2( 10× 11 + 10×8 + 11×8) - 10×11
= 2( 110+80+88)-110
= 2( 278) -110
= 556 -110
= 446ft²
The total surface area = 1006 + 446
= 1452 ft²
learn more about surface area from
https://brainly.com/question/16519513
#SPJ1
positive continous random variable with disbution and density we define in class the expected value to be prove, that given this definition:
Answers
Continuous random variable is a random variable that can take on a continuum of worth. In alternative words, a random variable is said to be continuous if it supposes a value that falls between a particular interval.
A continuous random variable can be described as a random variable that can take on an infinite number of possible values. Due to this, the probability that a continuous random variable will take on a fixed value is 0.
The probability density function of a continuous random variable can be explained as a function that gives the probability that the value of the random variable will drop between a range of values. Let X be the continuous random variable, then the formula for the pdf, f(x).
To know more about Continuous random variable:
https://brainly.com/question/17238189
#SPJ4
(-1,1)becames? (0,0)becomes?(1,1)becomes?
Answers
Answer:
(-1,1) becames 0, (0,0) becomes 0, (1,1) becomes 2
Trust Onepunchman (and maybe brainlist if I get it right)
Dhaulagiri is the 7th highest mountain in the world. Ms. Fink is walking through
the Hidden Valley, preparing for an ascent of the mountain. She looks up to the
mountain and measures the angle of elevation to be 47.3° and she knows she is
at an altitude of 4900m. She hikes 1000m closer to the mountain with no
elevation change and notes the angle of elevation to be 58.5°. How high above
sea level is Dhaulagiri?
Answers
Answer:
4833 m
Step-by-step explanation:
Given that her angle of elevation at the first recording is 47.3 at an altitude of 4900 m
We use Pythagoras Theorem to get this done
We can say that the opposite of the angle is the altitude, while the hypotenuse of the triangle, is the distance between herself and the top
Using the sine angle rule, we have
Sine 47.3 = 4900 / h
h = 4900 / sin 47.3
h = 4900 / 0.7349
h = 6668 m
This means that she was 6668 m away from the top of the mountain
She then moves 1000 m closer to the mountain top, this means that our h = 6668 - 1000
Using the same sine angle rule, we have
Sine 58.5 = o / 5668
o = 5668 * sine 58.5
o = 5668 * 0.8526
o = 4833 m
She is 4833 m above the sea level
The height h of an object thrown from the top of a ski lift 1240 feet high after t seconds is h=-16t2 +32t+1240. For what times is the height of the object at least 1000 feet?
←
The height of the object is at least 1000 feet from seconds to seconds.
Answers
Check the picture below.
so the parabolic path of the object is more or less like the one shown below in the picture, now this object has an initial of 1240 ft, as it gets thrown from the ski lift, so from 0 seconds is already higher than 1000 feet.
\(h=-16t^2+32t+1240\hspace{5em}\stackrel{\textit{a height of 1000 ft}}{1000=-16t^2+32t+1240} \\\\\\ 0=-16t^2+32t+240\implies 16t^2-32t-240=0\implies 16(t^2-2t-15)=0 \\\\\\ t^2-2t-15=0\implies (t-5)(t+3)=0\implies t= \begin{cases} ~~ 5 ~~ \textit{\LARGE \checkmark}\\ -3 ~~ \bigotimes \end{cases}\)
now, since the seconds can't be negative, thus the negative valid answer in this case is not applicable, so we can't use it.
So the object on its way down at some point it hit 1000 ft of height and then kept on going down, and when it was above those 1000 ft mark happened between 0 and 5 seconds.

What is the area of the figure?
7 in
Bin.
in
16 m
Answers
Answer:
112
Step-by-step explanation:\
Formula for Area- A(AREA)=L(LENGTH) times W(WIDTH)
If we follow this and plug in the Numbers we get the equasion- A=7x16
And so we solve and get the answer 112
hope this helped have a great day :3 (brainliest pls i need one more )
SOMEBODY HELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIEST
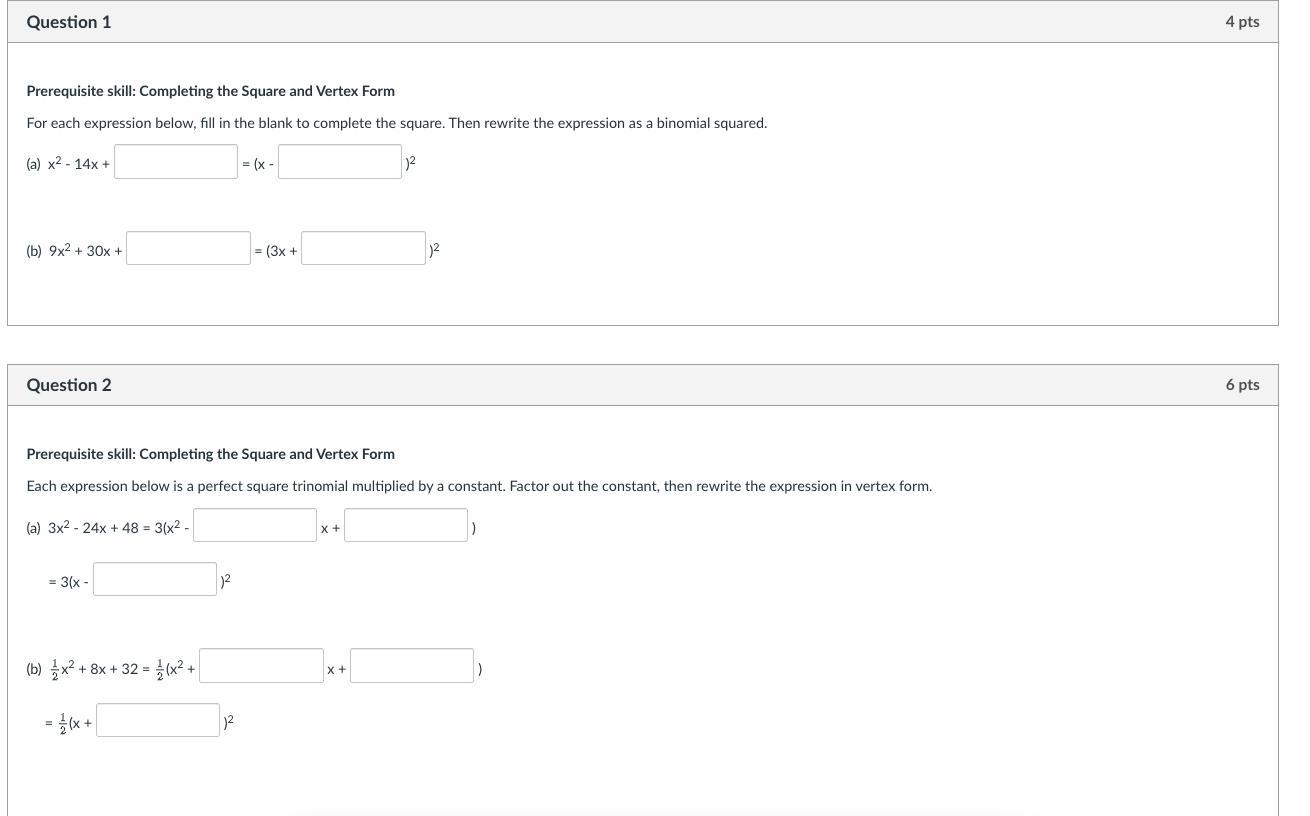
Answers
Answer:
\(\textsf{1.(a)} \quad x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
\(\textsf{1.(b)} \quad 9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\begin{aligned}\textsf{2.(a)}\quad3x^2-24x+48&=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\\&=3\left(x-\boxed{4}\right)^2\end{aligned}\)
\(\begin{aligned}\textsf{2.(b)}\quad \dfrac{1}{2}x^2+8x+32&=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\\&=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\end{aligned}\)
Step-by-step explanation:
Question 1(a) When completing the square for a quadratic equation in the form ax² + bx + c where the leading coefficient is one, we need to add the square of half the coefficient of the x-term:
\(x^2-14x+\left(\dfrac{-14}{2}\right)^2\)
\(x^2-14x+\left(-7\right)^2\)
\(x^2-14x+49\)
We have now created a perfect square trinomial in the form a² - 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Therefore:
\(a^2=x^2 \implies a=1\)
\(b^2=49=7^2\implies b = 7\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
(b) When completing the square for a quadratic equation where the leading coefficient is not one, we need to add the square of the coefficient of the x-term once it is halved and divided by the leading coefficient, and then multiply it by the leading coefficient:
\(9x^2 + 30x +9\left(\dfrac{30}{2 \cdot 9}\right)^2\)
\(9x^2 + 30x +9\left(\dfrac{5}{3}\right)^2\)
\(9x^2 + 30x +9 \cdot \dfrac{25}{9}\)
\(9x^2 + 30x +25\)
We have now created a perfect square trinomial in the form a² + 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 +2ab + b^2 = (a +b)^2}\)
Therefore:
\(a^2=9x^2 = (3x)^2 \implies a = 3x\)
\(b^2=25 = 5^2 \implies b = 5\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\hrulefill\)
Question 2(a) Factor out the leading coefficient 3 from the given expression:
\(3x^2-24x+48=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\)
We have now created a perfect square trinomial in the form a² - 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=3\left(x-\boxed{4}\right)^2\)
(a) Factor out the leading coefficient 1/2 from the given expression:
\(\dfrac{1}{2}x^2+8x+32=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\)
We have now created a perfect square trinomial in the form a² + 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2+2ab + b^2 = (a +b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\)
Step-by-step explanation:
Since ABCD is a rectangle
⇒ AB = CD and BC = AD
x + y = 30 …………….. (i)
x – y = 14 ……………. (ii)
(i) + (ii) ⇒ 2x = 44
⇒ x = 22
Plug in x = 22 in (i)
⇒ 22 + y = 30
⇒ y = 8
37.392 ÷ 0.09
Round your answer to the nearest hundredth..
Answers
Answer:
415.47
Step-by-step explanation:
37.392/0.09 which is 415.47( rounded)
Hope this helps hit the crown :D
Consider the function and its inverse: The slope, a, of the inverse function is , and the x-intercept of the inverse function is at x = .
Answers
Answer:
The slope, a, of the inverse function is 3 , and the x-intercept of the inverse function is at x = -2
Step-by-step explanation:
Many utility companies promote energy conservation by offering discount rates to consumers who keep their energy usage below certain established subsidy standards. A recent EPA report notes that 70% of the island residents of Puerto Rico hae reduced their electricity usage sufficiently to qualify for discounted rates. If five residential subscribers are randomly selected from San Juan, Puerto Rico, find the probability of each of the following events.a. All five qualify for the favorable rateb. At least four qualify for the favorable rates
Answers
Answer:
a. 0.1681 = 16.81% probability that all five qualify for the favorable rate.
b. 0.5283 = 52.83% probability that at least four qualify for the favorable rates
Step-by-step explanation:
For each Puerto Rico resident, there are only two possible outcomes. Either they qualify for discounted rates, or they do not. The probability of a person in the sample qualifying for discounted rates is independent of any other person in the sample. This means that the binomial probability distribution is used to solve this question.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
In which \(C_{n,x}\) is the number of different combinations of x objects from a set of n elements, given by the following formula.
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
And p is the probability of X happening.
70% of the island residents of Puerto Rico have reduced their electricity usage sufficiently to qualify for discounted rates.
This means that \(p = 0.7\)
Five residential subscribers are randomly selected from San Juan, Puerto Rico
This means that \(n = 5\)
a. All five qualify for the favorable rate
This is P(X = 5). So
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
\(P(X = 5) = C_{5,5}.(0.7)^{5}.(0.3)^{0} = 0.1681\)
0.1681 = 16.81% probability that all five qualify for the favorable rate.
b. At least four qualify for the favorable rates
This is
\(P(X \geq 4) = P(X = 4) + P(X = 5)\)
So
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
\(P(X = 4) = C_{5,4}.(0.7)^{4}.(0.3)^{1} = 0.3602\)
\(P(X = 5) = C_{5,5}.(0.7)^{5}.(0.3)^{0} = 0.1681\)
\(P(X \geq 4) = P(X = 4) + P(X = 5) = 0.3602 + 0.1681 = 0.5283\)
0.5283 = 52.83% probability that at least four qualify for the favorable rates
You will now consider Option 2-using low-flow shower heads instead of regular
shower heads.
Courtney claims that Option 2 would result in the class using 270 gallons of
water during 180 minutes of showering because:
(180minutes) (1.5gallons per minute) = 270gallons.
=
Courtney is incorrect.
• Identify her error.
• Explain how to find the correct amount of water used if the class
chooses Option 2.
• Include how much water would be used.
Answers
The error in Courtney claims that Option 2 would result in the class using 270 gallons is that he multiplied rather than dividing.
How to solve the error?From the information given, it should be noted that Courtney claims that Option 2 would result in the class using 270 gallons of water during 180 minutes of showering is incorrect because she should have divided and not multiplied. This will be:
= 270 / (3/2)
= 180 × 2/3
= 120
Therefore, 120 gallons will be used.
Learn more about division on:
https://brainly.com/question/25289437
#SPJ1
Suppose you flip a fair coin
1000 times. What do you think
is the probability of getting
exactly 500 heads?
Answers
Answer:
50
Step-by-step explanation:
first estimate probably 50% depends also in luck
Answer:
about 0.02
Step-by-step explanation:
If you toss a coin 1,000 times the average (mean) number of heads equals 500, yet the probability that you will get exactly 500 heads in 1,000 tosses is about 0.02.