Answers
Answer:
b.
Step-by-step explanation:
The function stops increasing when it reaches its peak at x = -1. The appropriate interval is the one shown in the attachment.
For x-values more positive than -1, the function is decreasing (has negative slope).

Related Questions
what is the area of this triangle?

Answers
Answer:
23,400
Step-by-step explanation:
30 times 30 times 26= 23,400
The volume of a cuboid is 540cm³. The length is 6cm and the width is 150mm. Work out the height of the cuboid in cm.
Answers
Step-by-step explanation:
To work out the height of the cuboid, we need to use the formula:
Volume = Length x Width x Height
We have been given the volume and the length, so we can substitute those values into the formula:
540 = 6 x Width x Height
Now we need to convert the width from millimeters to centimeters, so we divide it by 10:
150mm ÷ 10 = 15cm
Substituting this value into the formula:
540 = 6 x 15 x Height
Simplifying:
540 = 90 x Height
Dividing both sides by 90:
6 = Height
Therefore, the height of the cuboid is 6cm.
Help please:)
Graph the equation by plotting points.
X=4
Answers
Answer:
(4,0)
Step-by-step explanation:
You basically are plotting a point on the positive number 4 on the x line. Since they're only asking for an X and not a Y, you'd leave it as (4,0). Hope this helps!
HELP
What is the equation of the trend line in the scatter plot ?

Answers
Answer:
its decreasing
Step-by-step explanation:
the graph will always be read from left to right.
The value of a stock over a 12 year period form 2003 to 2015 is shown in the line graph. Which statement is not supported by the graph?

Answers
Answer:
an individual who invested in the market in 2006 has yet to regain the losses incurred in 2008
Step-by-step explanation:
which of the following pairs of variables is likely to have a negative correlation? check all that apply.
Answers
The two variables to have a negative correlation are x and y.
Negative correlation is the relationship where x grows as y decreases.
Given,
Here, negative correlation is used to describe the relationship between two variables that results in independent variables moving in one direction while dependent variables move in another.
Positive correlation
Positive correlation is when the value of the variable x rises as the value of the variable y rises.
Negative Correlation
Negative correlation is the relationship where x grows as y decreases.
No correlation
No correlation exists between the two variables.
That example, the term "no-correlation" refers to the absence of a connection between two variables.
Learn more about correlation here;
https://brainly.com/question/20319174
#SPJ4
The question is improper. Proper question is given below;
What two variables are likely to have a negative correlation
NO LINKS!! URGENT HELP PLEASE!!
1. Find the area of a regular octagon. Each side is 12 m.
2. The perimeter of a regular polygon is 72 feet. An exterior angle of the polygon measures 40°. Find the length of each side.
3. If the perimeter of a regular pentagon is 50 in. Find the area. Show a drawing and work please.
Answers
Answer:
1) 695.3 m²
2) 8 ft
3) 172.0 in²
Step-by-step explanation:
Question 1To find the area of a regular polygon, we can use the following formula:
\(\boxed{\begin{minipage}{5.5cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{s^2n}{4 \tan\left(\dfrac{180^{\circ}}{n}\right)}$\\\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\end{minipage}}\)
Given the polygon is an octagon, n = 8.
Given each side measures 12 m, s = 12.
Substitute the values of n and s into the formula for area and solve for A:
\(\implies A=\dfrac{(12)^2 \cdot 8}{4 \tan\left(\dfrac{180^{\circ}}{8}\right)}\)
\(\implies A=\dfrac{144 \cdot 8}{4 \tan\left(22.5^{\circ}\right)}\)
\(\implies A=\dfrac{1152}{4 \tan\left(22.5^{\circ}\right)}\)
\(\implies A=\dfrac{288}{\tan\left(22.5^{\circ}\right)}\)
\(\implies A=695.29350...\)
Therefore, the area of a regular octagon with side length 12 m is 695.3 m² rounded to the nearest tenth.
\(\hrulefill\)
Question 2The sum of an interior angle of a regular polygon and its corresponding exterior angle is always 180°.
If the exterior angle of a polygon measures 40°, then its interior angle measures 140°.
To determine the number of sides of the regular polygon given its interior angle, we can use this formula, where n is the number of sides:
\(\boxed{\textsf{Interior angle of a regular polygon} = \dfrac{180^{\circ}(n-2)}{n}}\)
Therefore:
\(\implies 140^{\circ}=\dfrac{180^{\circ}(n-2)}{n}\)
\(\implies 140^{\circ}n=180^{\circ}n - 360^{\circ}\)
\(\implies 40^{\circ}n=360^{\circ}\)
\(\implies n=\dfrac{360^{\circ}}{40^{\circ}}\)
\(\implies n=9\)
Therefore, the regular polygon has 9 sides.
To determine the length of each side, divide the given perimeter by the number of sides:
\(\implies \sf Side\;length=\dfrac{Perimeter}{\textsf{$n$}}\)
\(\implies \sf Side \;length=\dfrac{72}{9}\)
\(\implies \sf Side \;length=8\;ft\)
Therefore, the length of each side of the regular polygon is 8 ft.
\(\hrulefill\)
Question 3The area of a regular polygon can be calculated using the following formula:
\(\boxed{\begin{minipage}{5.5cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{s^2n}{4 \tan\left(\dfrac{180^{\circ}}{n}\right)}$\\\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\end{minipage}}\)
A regular pentagon has 5 sides, so n = 5.
If its perimeter is 50 inches, then the length of one side is 10 inches, so s = 10.
Substitute the values of s and n into the formula and solve for A:
\(\implies A=\dfrac{(10)^2 \cdot 5}{4 \tan\left(\dfrac{180^{\circ}}{5}\right)}\)
\(\implies A=\dfrac{100 \cdot 5}{4 \tan\left(36^{\circ}\right)}\)
\(\implies A=\dfrac{500}{4 \tan\left(36^{\circ}\right)}\)
\(\implies A=\dfrac{125}{\tan\left(36^{\circ}\right)}\)
\(\implies A=172.047740...\)
Therefore, the area of a regular pentagon with perimeter 50 inches is 172.0 in² rounded to the nearest tenth.
Answer:
1.695.29 m^2
2.8 feet
3. 172.0477 in^2
Step-by-step explanation:
1. The area of a regular octagon can be found using the formula:
\(\boxed{\bold{Area = 2a^2(1 + \sqrt{2})}}\)
where a is the length of one side of the octagon.
In this case, a = 12 m, so the area is:
\(\bold{Area = 2(12 m)^2(1 + \sqrt{2}) = 288m^2(1 + \sqrt2)=695.29 m^2}\)
Therefore, the Area of a regular octagon is 695.29 m^2
2.
The formula for the exterior angle of a regular polygon is:
\(\boxed{\bold{Exterior \:angle = \frac{360^o}{n}}}\)
where n is the number of sides in the polygon.
In this case, the exterior angle is 40°, so we can set up the following equation:
\(\bold{40^o=\frac{ 360^0 }{n}}\)
\(n=\frac{360}{40}=9\)
Therefore, the polygon has n=9 sides.
Perimeter=72ft.
We have
\(\boxed{\bold{Perimeter = n*s}}\)
where n is the number of sides in the polygon and s is the length of one side.
Substituting Value.
72 feet = 9*s
\(\bold{s =\frac{ 72 \:feet }{ 9}}\)
s = 8 feet
Therefore, the length of each side of the polygon is 8 feet.
3.
Solution:
A regular pentagon has five sides of equal length. If the perimeter of the pentagon is 50 in, then each side has a length = \(\bold{\frac{perimeter}{n}=\frac{50}{5 }= 10 in.}\)
The area of a regular pentagon can be found using the following formula:
\(\boxed{\bold{Area = \frac{1}{4}\sqrt{5(5+2\sqrt{5})} *s^2}}\)
where s is the length of one side of the Pentagon.
In this case, s = 10 in, so the area is:
\(\bold{Area= \frac{1}{4}\sqrt{5(5+2\sqrt{5})} *10^2=172.0477 in^2}\)
Drawing: Attachment

Find the volume
(65 points)

Answers
Answer: 62.83 (rounded)
Step-by-step explanation:
The formula for volume in spheres is V = \(\frac{4}{3}\) \(\pi\) \(r^{2}\)
r = radius
So, we can just plug that in into
\(\frac{4}{3} \pi\) \((15)^{2}\)
V = 62.831853
explain the types of frequency distribution in statistics
Answers
The two types of frequency distributions are Discrete Frequency Distribution and Grouped Frequency Distribution
What are the types of distribution?The two types of frequency distributions are;
Discrete Frequency Distribution:Grouped Frequency DistributionWhen the data consists of discrete, separate values, this sort of distribution is used. It displays the frequency or number of occurrences of each value.
The data is often expressed in a table with two columns: one for distinct values and another for the frequencies of those values.
This distribution is utilized when the data is continuous and has a wide range of values. It entails categorizing the data into intervals or classes and then calculating the frequency of values that fall within each interval.
Learn more about frequency distribution at: https://brainly.com/question/27820465
#SPJ1
solve for x
(look at photo)

Answers
By definition of proportion, the value of x is,
⇒ x = 80
We have to given that;
In a triangle,
Perpendicular = 60
Now, By Pythagoras theorem we get;
60² = 36² + y²
3600 = 1296 + y²
y² = 3600 - 1296
y² = 2304
y = 48
Hence, By definition of proportion;
⇒ x / 48 = 60 / 36
⇒ x = 80
Thus, By definition of proportion, the value of x is,
⇒ x = 80
Learn more about the proportion visit:
https://brainly.com/question/1496357
#SPJ1
The circumference of a circle is 15pi centimeters what is the area of the circle in terms of pi?
Answers
\(\textit{circumference of a circle}\\\\ C=2\pi r ~~ \begin{cases} r=radius\\[-0.5em] \hrulefill\\ C=15\pi \end{cases}\implies 15\pi =2\pi r\implies \cfrac{15\pi }{2\pi }=r\implies \cfrac{15}{2}=r \\\\[-0.35em] ~\dotfill\\\\ \textit{area of a circle}\\\\ A=\pi r^2 \begin{cases} r=radius\\[-0.5em] \hrulefill\\ r=\frac{15}{2} \end{cases}\implies A=\pi \left( \cfrac{15}{2} \right)^2\implies A=\cfrac{225\pi }{4}\implies A=56.25\pi\)
Math question....................
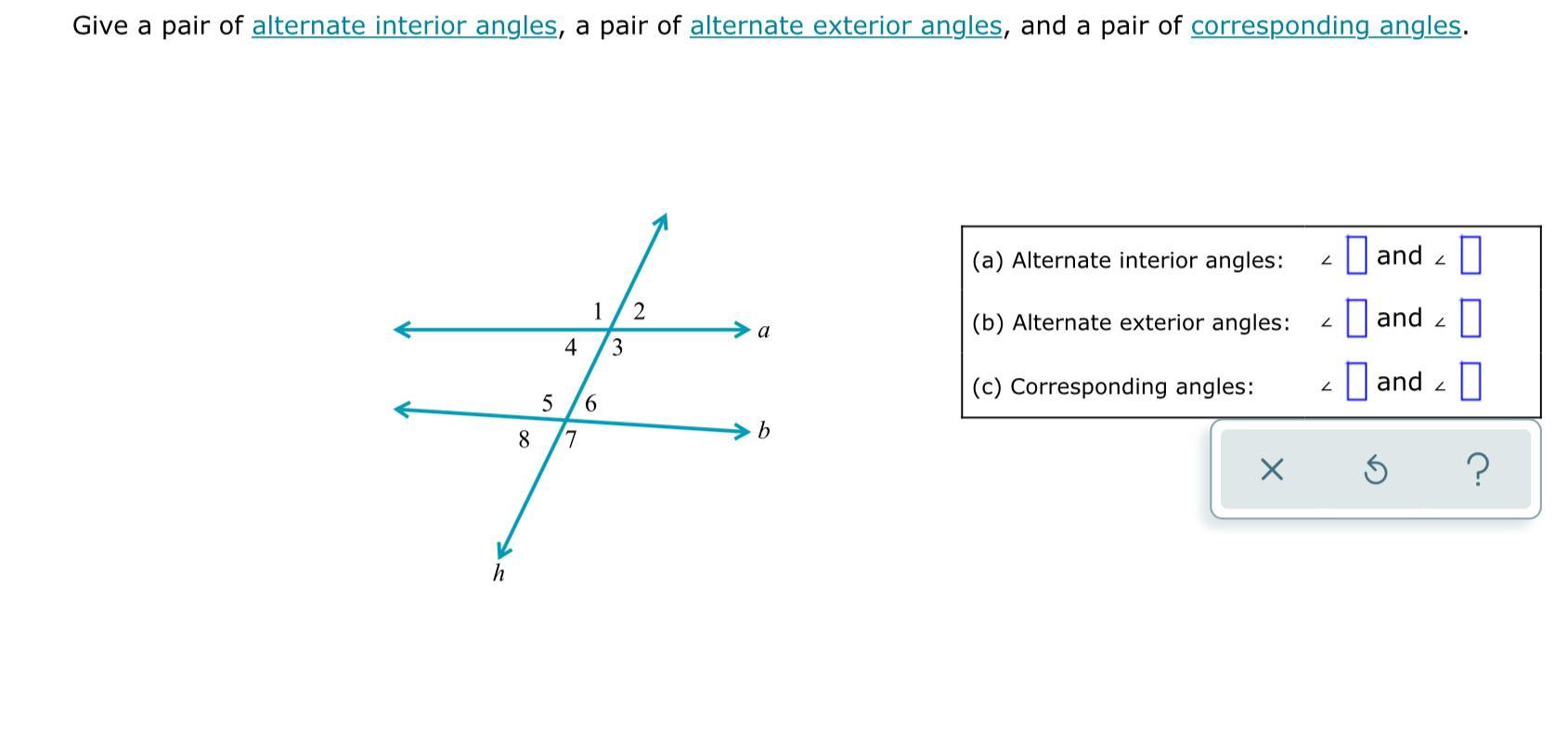
Answers
\(alternative \: interior \: angles\)
<4 and <6
\(alternative \: exterior \: angles\)
<1 and <7
\(corresponding \: angles\)
<1 and <5
Use the percent formula, A =PB: A is P percent of B, to answer the following question.
22% of what number is 37.4?
22% of _ is 37.4
Answers
Use the percent formula, A =PB: A is P percent of B, 22% of approximately 170 is equal to 37.4.
To find the number, let's use the percent formula:
A = P * B
where A is the value we are trying to find, P is the percentage (in decimal form), and B is the total.
In this case, we are given that 22% of a certain number is equal to 37.4. So we have:
A = 0.22 * B
We want to solve for B, so we can rearrange the formula:
B = A / 0.22
Substituting A = 37.4 into the equation:
B = 37.4 / 0.22
Calculating this:
B ≈ 170
Therefore, 22% of approximately 170 is equal to 37.4.
for such more question on percentage
https://brainly.com/question/24877689
#SPJ8
A particle moves on a straight line and has acceleration a(t)=24t+2. Its position at time t=0 is s(0)=3 and its velocity at time t=0 is v(0)=13. What is its position at time t=5?
Answers
Answer:
It's position at time t = 5 is 593.
Step-by-step explanation:
The velocity v(t) is the integral of the acceleration a(t)
The position s(t) is the integral of the velocity v(t)
We have that:
The acceleration is:
\(a(t) = 24t + 2\)
Velocity:
\(v(t) = \int {a(t)} \, dt = \int {24t + 2} \, dt = 12t^{2} + 2t + K\)
K is the initial velocity, that is v(0). Since V(0) = 13, K = 13
Then
\(v(t) = 12t^{2} + 2t + 13\)
Position:
\(s(t) = \int {s(t)} \, dt = \int {12t^{2} + 2t + 13} \, dt = 4t^{3} + t^{2} + 13t + K\)
Since s(0) = 3
\(s(t) = 4t^{3} + t^{2} + 13t + 3\)
What is its position at time t=5?
This is s(5).
\(s(t) = 4t^{3} + t^{2} + 13t + 3\)
\(s(5) = 4*5^{3} + 5^{2} + 13*5 + 3\)
\(s(5) = 593\)
It's position at time t = 5 is 593.
please help guys asap
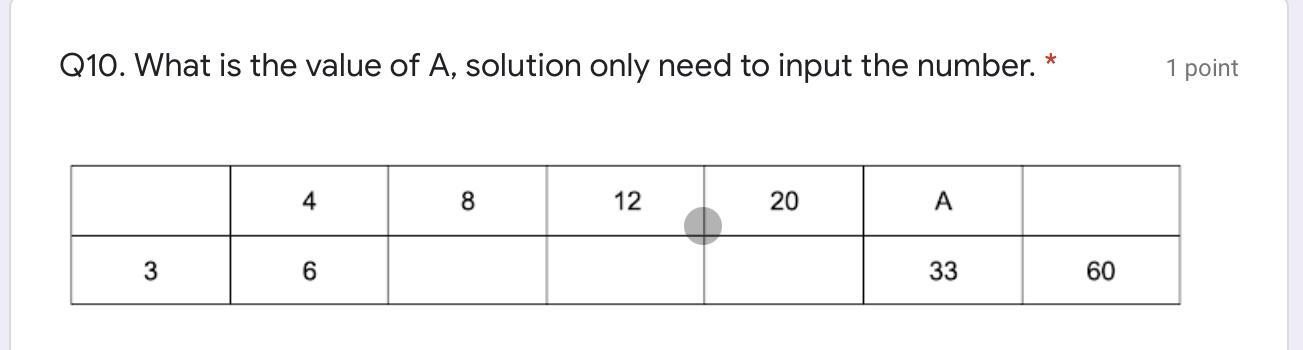
Answers
Answer:
28 i think
Step-by-step explanation:
PLEASE HELP URGENT !! (What is the slope of the line on the graph?)
What is the slope of the line on the graph?

Answers
Answer:
2/6
1/3 simplified
Rise over run
choose any two points on the graph and do rise over run
Match each function on the left to all points on the right that would be located on the graph of the function. Help!! thanks

Answers
Each function on the left should be matched to all points on the right that would be located on the graph of the function as follows;
f(x) = 2x + 2 ⇒ (0, 2).
f(x) = 2x² - 2 ⇒ (-1, 0).
\(f(x) = 2\sqrt{x+1}\) ⇒ (0, 2).
What is a function?In Mathematics and Geometry, a function is a mathematical equation which defines and represents the relationship that exists between two or more variables such as an ordered pair in tables or relations.
Next, we would determine the point or ordered pair that represent a solution on the graph of each of the function as follows;
For the ordered pair (0, 2), we have:
f(x) = 2x + 2
2 = 2(0) + 2
2 = 2 (True).
For the ordered pair (-1, 0), we have:
f(x) = 2x² - 2
0 = 2(-1)² - 2
0 = 2 - 2
0 = 0 (True).
For the ordered pair (0, 2), we have:
\(f(x) = 2\sqrt{x+1}\\\\2= 2\sqrt{0+1}\\\\2 = 2\sqrt{1}\)
2 = 2 (True).
Read more on function here: https://brainly.com/question/10687170
#SPJ1
a = root 2
b = root 5
c = root 10
ac/b = ?

Answers
Answer:
The answer is 2
Step-by-step explanation:
Given:
a = √2
b = √5
c = √10 = (√2 × √5)
Now,
ac/b
= √2√10 ÷ √5
= √2 × √2 × √5 ÷ √5
= √2 × √2 = √4 = 2
Thus, The answer is 2
-TheUnknownScientist
Answer:
2
Step-by-step explanation:
√2*√10
=4.471/2.236
=1.999
approximately =2
What is the expression equivalent too?

Answers
Answer:
x+5
Step-by-step explanation:
3(x+4)-(2x+7)
1. Distribute 3 to x and 4
3x+12-2x+7
2. Distribute the "-" to 2x and 7
2x+12-2x-7
3. Subtract 7 from 12
3x+12-2x-7
3x+5-2x
4. Combine like terms
3x+5-2x
1x+5
Answer:
x+5
A pen is $1 cheaper than a stapler. Their total price is $5.20. Find the price of the pen.
Answers
Help pls show work if needed!

Answers
Answer:
d = 50h
Step-by-step explanation:
We are using the linear property y = mx.
We know that distance = rate × time, so if we subsitute this, we get that the distance is d, the rate is 50 mph, and the time is h.
Therefore, we can form the equation d = 50h.
Scores on a recent national statistics exam were normally distributed with a mean of 82.2 and a standard deviation of 5.If the top 2.5% of test scores receive merit awards, what is the lowest score eligible for an award
Answers
Answer:
The lowest score eligible for an award is 92.
Step-by-step explanation:
When the distribution is normal, we use the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
In this question:
\(\mu = 82.2, \sigma = 5\)
If the top 2.5% of test scores receive merit awards, what is the lowest score eligible for an award
The lowest score is the 100 - 2.5 = 97.5th percentile, which is X when Z has a pvalue of 0.975. So X when Z = 1.96. Then
\(Z = \frac{X - \mu}{\sigma}\)
\(1.96 = \frac{X - 82.2}{5}\)
\(X - 82.2 = 5*1.96\)
\(X = 92\)
The lowest score eligible for an award is 92.
Magician Anthony has in his magic hat 14 grey, 8 white and 6 black mice. What is
the least number of mice he has to take out of his hat blindfolded to be absolutely
certain that he has got at least one mouse of each colour?
Answers
The least number of mice that he has to take out of his hat would be 23.
How to solve for the least number of miceWe have the following details to solve this problem
x = 14
t = 8
u = 6
n1 = x + t + 1
= 14 + 8 + 1 = 23
n2 = t + u + 1
= 8 + 6 + 1 = 15
n3 = x + u + 1
= =14+6+1=21
From here the
max n (n1, n2, n3) = 23, 15, 21
Hence the least number that has to be taken out would be 23.
Read more on least numbers here:
https://brainly.com/question/694446
#SPJ1
What is wrong with the following proof? Clearly we know that 1 does not equal 2. What rule of algebra did we break that makes this conclusion invalid? I've numbered the lines for you so you can refer to the line numbers in your explanation

Answers
An attempt to divide by zero gives a contradictory result
A rule of algebra broken is dividing by zero (leading to a contradiction) and stating a finite result
Reason:
The given calculation is presented as follows;
1. a > 0, b > 0 given
2. a = b given
3. a·b = b²
4. a·b - a² = b² - a²
5. a·(b - a) = (b + a)·(b - a)
6. a = b + a
7. 0 = b
8. b = 2·b
9. 1 = 2
From line 4, the result are;
4. a·b - a² = b² - a² = 0
5. a·(b - a) = (b + a)·(b - a) = 0
On line 6, both sides where divided by (b - a) = 0, which should given an infinite result
Therefore, one rule of algebra broken is dividing by zero to get a finite result
In line 7, we have;
7. 0 = b
From 6. a = b + a, and a = b, we have;
8. b = 2·b
Therefore, line 9 should be;
9. 0 = 2·0; 0 = 0, given that we have;
1 × 0 = 0
2 × 0 = 0
∴ 1 × 0 = 2 × 0
However
1 ≠ 2In line 9., by dividing by b = 0, again, we have;
9. 1 = 2 (a contradiction)Therefore, one rule of algebra that is broken is dividing by zero and having a finite result
Learn more about the rules of algebra here:
https://brainly.com/question/11388301
Given a number n, for each integer i in the range from 1 to n inclusive, print one value per line as follows: • If iis a multiple of both 3 and 5, print FizzBuzz. • If iis a multiple of 3 (but not 5), print Fizz. • If iis a multiple of 5(but not 3), print Buzz. • If i is not a multiple of 3 or 5, print the value ofi. Function Description Complete the function fizzBuzz in the editor below. fizzBuzz has the following parameter(s): int n: upper limit of values to test (inclusive) Returns: NONE Prints: The function must print the appropriate response for each value i in the set {1, 2, ... n}in ascending order, each on a separate line. Constraints • 0
Answers
The program is an illustration of loops and conditional statements and the part of the complete program is
n = int(input())
for i in range(1,n+1):
if not(i%3 == 0 or i%5==0):
How to determine the program using the conditions?The program written in Python where comments are used to explain each line is as follows:
#This gets input for n
n = int(input())
#This iterates through n
for i in range(1,n+1):
#If the current number is not a multiple of 3 and 5
if not(i%3 == 0 or i%5==0):
#This prints the number
print(i,end="")
else:
#This prints "Fizz", if the current number is a multiple of 3
if i%3 == 0:
print("Fizz",end="")
#This prints "Buzz", if the current number is a multiple of 5
if i%5==0:
print("Buzz",end="")
#This prints a new line
print()
Read more about loops and conditional statements at:
brainly.com/question/26098908
#SPJ1
Question:
Determine whether this table represents a probability distribution.
x P(x)
0 0.3
1 0.3
2 0.1
3 0.3
Ans:
Yes, it is a probability distribution
Answers
According to given information, this table represents a probability distribution.
What is probability distribution?
A probability distribution is a function that describes the likelihood of different outcomes in a random event. It gives us a way to assign probabilities to each possible outcome in a sample space, which is the set of all possible outcomes. In a probability distribution, each possible outcome is associated with a probability, and the probabilities of all possible outcomes sum to 1.
To determine whether this table represents a probability distribution, we need to check two things:
The sum of all probabilities is equal to 1.
All probabilities are non-negative.
Let's check these two conditions:
Sum of all probabilities = 0.3 + 0.3 + 0.1 + 0.3 = 1. This condition is met.
All probabilities are non-negative, and each probability is less than or equal to 1. This condition is also met.
Therefore, this table represents a probability distribution.
To learn more probability distribution visit:
https://brainly.com/question/23286309
#SPJ1
A single die is rolled. Find the odds in favor of rolling a number greater than 3.
Answers
Answer:
6:3
Step-by-step explanation:
Answer and Step-by-step explanation:
3 of the options are not to be chosen, and 3 are wanted.
That means that anything above 3 (so, 4, 5, or 6) are the numbers that are wanted, while the numbers 1, 2, and 3 are not wanted.
We have 6 total options.
The ration would be:
3:6, or 3 to 6. This reduces down to 1:2, or 1 to 2.
That means that there is a 50% chance of getting 4, 5, or 6.
#teamtrees #PAW (Plant And Water)
An artist's canvas has sides measuring 3x + 5 and 2x + 1 inches.
What is the area of the canvas? Show all work.
The artist laid the canvas flat on the floor and poured some paint in the center. The paint flows at a rate of r(t) = 2t where t represents time in minutes and r represents how far the paint is spreading on the canvas. The area of the paint can be expressed as A[r(t)]= rur?. What is the area of the circle created by the paint?
If the artist wants the circle to be at least 300 in?, will it be that large in 5 minutes? Support your answer with your work.
Answers
The area of the circle created by the paint is given by the expression 4πt².
The area of the circle is 100π, which is approximately 314.16 in².
The circle will be at least 300 in² in 5 minutes. Yes.
To find the area of the canvas, we multiply the lengths of its sides:
Area = (3x + 5) × (2x + 1)
Expanding the expression:
Area = 6x² + 3x + 10x + 5
Combining like terms:
Area = 6x² + 13x + 5
The area of the canvas is given by the expression 6x² + 13x + 5.
Now, let's find the area of the circle created by the paint.
The area of a circle is given by the formula A = πr², where r represents the radius.
The radius is given by the spreading of paint, which is r(t) = 2t.
Substituting the value of r(t) into the formula, we have:
A[r(t)] = π(2t)²
Simplifying:
A[r(t)] = π(4t²)
A[r(t)] = 4πt²
Now, let's determine if the area of the circle will be at least 300 in² in 5 minutes.
Substitute t = 5 into the area formula:
A[r(5)] = 4π(5)²
A[r(5)] = 4π(25)
A[r(5)] = 100π
Since 314.16 in² is larger than 300 in², the circle created by the paint will be larger than 300 in² in 5 minutes.
For similar questions on area of the circle
https://brainly.com/question/12269818
#SPJ8
A survey of 200 people found 135 like horses, 75 like camels, and 23 like both animals. How many like neither?
Answers
Answer:
13
Step-by-step explanation:
If 23 like both animals, then the total number of people who like both animals is:
(75 - 23) + (135 - 23) + 23 = 187
Subtract 187 from the total number of people in the survey to find how many like neither:
200 - 187 = 13
Sketch and shade the region in the xy-plane defined by the equation or inequalities.
|x| < 7 and |y| < 3 g
Answers
Answer:
attached below is the solution
Step-by-step explanation:
|x| < 7
= -7 < x < 7
| y | < 3
= -3< y < 3
attached below is the shaded region in the xy-plane

