What is the product of -9.56 x 8.5? A. -81.26 B. -73.06 C. 81.26 D. 73.06
Answers
Answer:
A -81.26
Step-by-step explanation:
Answer:
The answer is, A.) -81.26!
Step-by-step explanation:
I got it right on the test. Please mark me branliest!
A. √
B. ×
C. ×
D. ×
Related Questions
Which of the following are solutions to the system of inequalities y<−x+5 and y≥3x+1?
A)
(1,0)
cross out
B)
(−2,2)
cross out
C)
(1,6)
cross out
D)
(0,1)
cross out
E)
(1,4)
cross out
F)
(−2,7)
Answers
From the graph attached below, the solution to the system of linear inequalities are (1, 4)
What is the solution to the system of linear inequalities?A system of linear inequalities is a collection of linear inequalities in the same variables. The solution is any ordered pair that satisfies each of the inequalities.
In the problem given;
y < - x + 5 ...eq(i)
y ≥ 3x + 1 ...eq(ii)
To determine the solution to the system of linear inequalities, it is easier for us to use graphical method. This is simply done by plotting the points and determine the coordinate at which both inequalities intersect.
From the graph of the system of linear inequalities, the solution to this is (1, 4) which is option E
Kindly find attached graph below
Learn more on system of linear inequalities here;
https://brainly.com/question/23093488
#SPJ1

The diameter of the circle above is 14 cm. What is the circumference of the circle? Use a = 3.14.
Circumference 2пт
A. 153.86 cm
B. 21.98 cm
C. 43.96 cm
D. 307.72 cm
Answers
Answer:
43.96 or C
Step-by-step explanation:
c=(pi)(d)
pi --> 3.14
d --> diameter (in your case 14.)
c=3.14*14
c= 43.96
Both formulas work, 2(pi)r and (pi)(d)
But, if they give you the diameter then use (pi)(d).
If they give you the radius then use 2(pi)r
Consider the function f(x)=2x−−√−8. If f−1(x) is the inverse function of f(x), find f−1(2)
Answers
\(f^(-1)(2) = 6\), which is consistent with our earlier result.
What is inverse function?A function that "undoes" another function is known as an inverse function. If f(x) is a function, then f(x inverse, )'s indicated by f-1(x), is a function that accepts f(x output )'s as an input and outputs f(x initial )'s input.
Given the function f(x) = √(2x - 8), if f^(-1)(x) is the inverse function of f(x), what is \(f^(-1)(2)\)?
Solution:
To find f^(-1)(2), we need to find the value of x such that \(f(x) = 2\) . We can set up an equation:
\(f(x) = \sqrt(2x - 8) = 2\)
Squaring both sides, we get:
\(2x - 8 = 4\)
\(2x = 12\)
\(x = 6\)
Therefore, \(f^(-1)(2) = 6.\)
We can also verify this result by using the definition of an inverse function. If f^(-1)(x) is the inverse function of f(x), then by definition:
\(f(f^(-1)(x)) = x\)
We can substitute x = 2 and solve for f^(-1)(2):
\(f(f^(-1)(2)) = 2\)
\(f^(-1)(2) = (f(6))^(-1)\)
f(6) = √(2(6) - 8) = √4 = 2
Therefore,\(f^(-1)(2) = 6\), which is consistent with our earlier result.
Learn more about function here:
https://brainly.com/question/2541698
#SPJ1
6 x 6 x 6 x 6 x 6 x 6 x 6= 6^x
Answers
Answer:
\( 6^7 \)
Step-by-step explanation:
\(6 \times 6 \times 6 \times 6 \times 6 \times 6 \times 6 = 6^7 \\ \)
Hey there!
6 * 6 * 6 * 6 * 6 * 6 * 6 ➡️ 6^7
= 36 * 36 * 36 * 6
= 1,296 * 36 * 6
= 46,656 * 6
= 279,936
Therefore, your answer is: 6^7
Good luck on your assignment & enjoy your day!
~Amphitrite1040:)
Need help with the answer

Answers
Answer:
C
Step-by-step explanation:
The slope is: (y2 - y1) ÷ (x2-x1)
In this question y2 is 5, y1 is 8, x2 is 0, and x1 is -3.
5-8=-3
0-(-3)=3
-3 ÷ 3 = -1
the slope is negative 1
z InstructionsO ptsQuestion 1What is the y-intercept?- 101X25у678No new data to save. Last checked at 4:51 pmSubmit

Answers
To find the y-intercept we need to remember that this happens when x=0. Then, in our case, the y-intercept is 6.
How many solutions are there to the equation below? x2 = 16 A.2 B.4 C.16 D.1 E.0
Answers
Answer:
2
Step-by-step explanation:
x^2 = 16
x = + √16
x = + 4
therefore
x= -4 or 4
there are 2 solutions in the equation
If x varies directly as y, find x when y = 8 a) x = 6 when y = 32 b) x = 14 when y = -2
Answers
a) The value of x is 42.6 when k =16/3 is directly proportional to y.
b) The value of x is -56 when k is -7 is directly proportional to y.
What kind of variation is one where x and y are directly proportional?
If x = ky for some constant k can be used to indicate the relationship between the variables y and x, then we may say that y varies directly with y or that x is directly proportional to y.x varies directly as y
x α y
x = ky
a) x=6 ; y = 32
x = ky
6 = k(32)
k = 16/3
if y = 8
then,
x = (16/3) * 8
= 128/3
x = 42.6
Hence, the value of x is 42.6 when k =16/3 is directly proportional to y.
b) x= 14 and y = -2
x = ky
14 = k(-2)
k = -7
if y = 8
then,
x = ky
x= (-7) 8
x = -56
Hence, the value of x is -56 when k is -7 is directly proportional to y.
To know more about proportional check the below link:
https://brainly.com/question/870035
#SPJ1
I need help on all of them I’ll take some if not all!

Answers
Note that the angles are found using the principle of the circle theorems.
What are the measure of the angels given?The angle of the circumference is half of the angle at the center of the circle by an arc.
AB = 78°
∠5 = 39°
Angles intercepted by the same arc are equal.
∠4 = 39°
FE= 105°
∠16 =105°
ED = 27°
∠17 =27°
CD = 42°
∠10 =21°
∠3 =21°
The angle of the semi-circle is 90°.
∠2 =90°
∠8=∠9 = (180-48)/2
∠8= 66°
∠9= 66°
∠7=90°-∠8 = 90°-66°
∠7=24°
∠17 = 180°-∠15-∠16
∠17 = 180°-48°-105°
∠17 =27°
∠6=∠15/2 = 48/2
∠6=24°
∠21 = 180°-∠7-∠16
∠21 = 180°-24°-105°
∠21 =51°
∠19 =51°
∠18 = 180°-∠17-∠6
∠18 = 180°-27°-24°
∠18 = 129°
∠20 = 129°
BC = 60°
∠1 = 60/2
∠1 =30°
∠11=180°-∠1-∠2
∠11=180°-30°-90°
∠11=60°
∠13=60°
∠12=180-∠11
∠12=180°-60°
∠12=120°
∠14=120°
∠15=48°
Learn more about circle theorem:
https://brainly.com/question/31703930
#SPJ1
Given 3 + 7 + 11 + 15 + … find S20
Answers
Answer:
Hi
Please mark brainliest ❣️
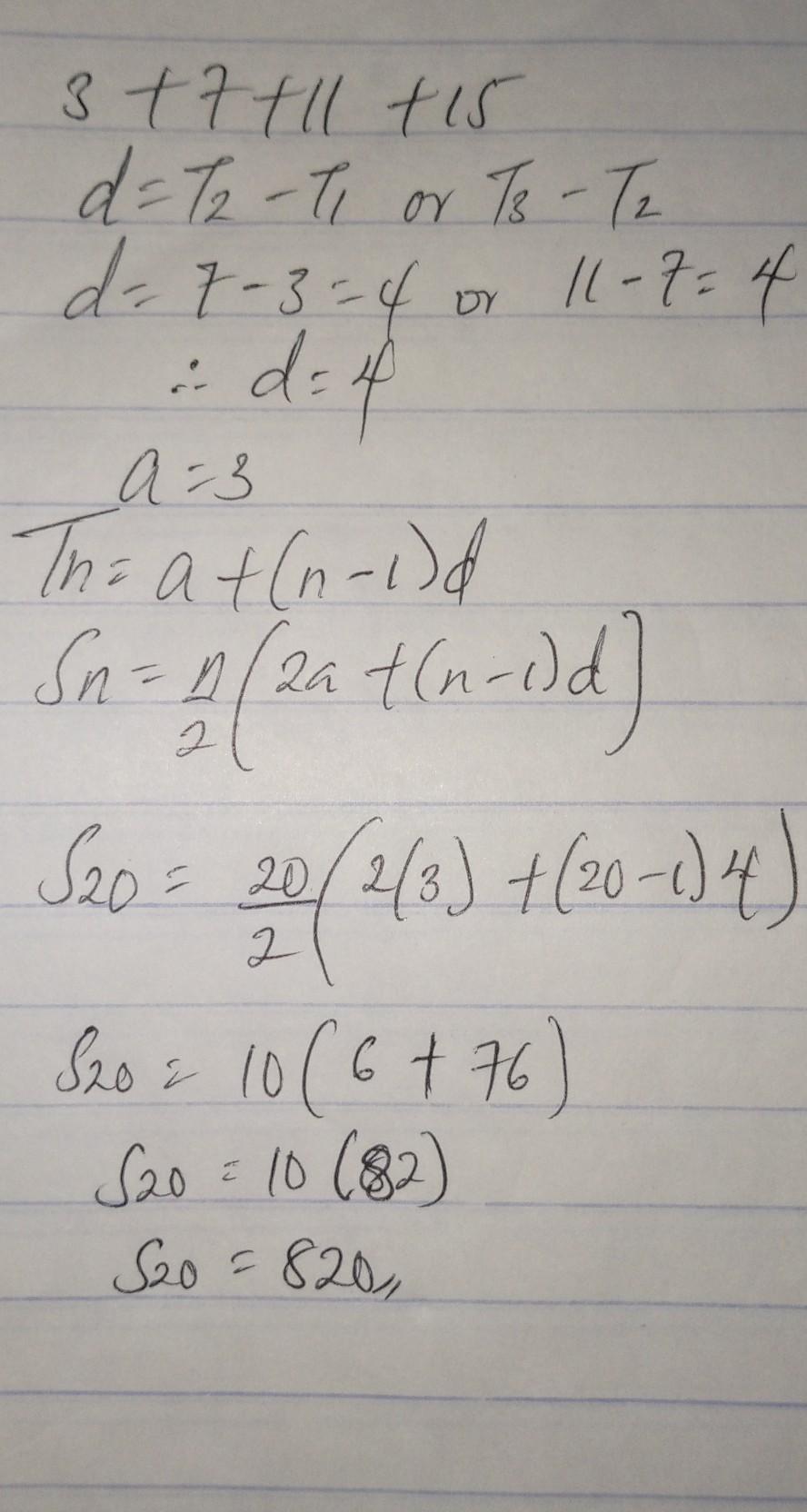
A crayon is shown here.
2 cm
12 cm
1.5 cm
There are 24 crayons in a box. What is the approximate total volume of the crayons?
Answers
one of the acute angles has a measure of 31°.
If the opposite side measures 42 cm, what is the length of the adjacent side?
Answers
The length of the adjacent side is approximately 69.94 cm.
To find the length of the adjacent side, we can use the trigonometric function called tangent.
The tangent of an acute angle is defined as the ratio of the length of the opposite side to the length of the adjacent side.
Given that one acute angle has a measure of 31° and the length of the opposite side is 42 cm, we need to find the length of the adjacent side.
Let's denote the length of the adjacent side as 'x'.
Using the tangent function, we have:
tan(31°) = opposite side / adjacent side
tan(31°) = 42 cm / x
To solve for 'x', we can rearrange the equation:
x = 42 cm / tan(31°)
Now, let's calculate the value of 'x' using a calculator:
x ≈ 42 cm / 0.6009
x ≈ 69.94 cm (rounded to two decimal places).
For similar question on trigonometric function.
https://brainly.com/question/29718746
#SPJ8
Archimedes went to sleep beside a big rock. He wanted to get up at 7 77 AM, but the alarm clock was yet to be invented! He decided to sleep at the spot where the rock's shadow should end when it's 7 77 AM so as to be awakened by the direct sunlight. Archimedes knew that at 7 77 AM, the sunlight reaches the ground at an angle of 3 1 ∘ 31 ∘ 31, degrees. The rock beside which he slept was 5 55 meters tall. How far from the rock did Archimedes go to sleep? Round your final answer to the nearest hundredth.
Answers
Archimedes went to sleep about 9.24 meters away from the rock where its shadow should end when it was 7 AM.
Trigonometric ratios:Trigonometric ratios are ratios of the sides of a right triangle to its angles. The three primary trigonometric ratios are
Sine = opposite/hypotenuse.
Cosine = adjacent/hypotenuse.
Tangent = opposite/adjacent.
Here we have
Archimedes wanted to get up at 7. AM, but the alarm clock was yet to be invented. Archimedes knew that at 7.AM, the sunlight reaches the ground at an angle of 31°.
The rock beside which he slept was 5.55 meters tall.
Let's assume that the distance from the rock where Archimedes went to sleep is "x".
Form a right triangle where the height of the triangle is the height of the rock (5.55 meters) and the angle between the ground and the sunlight at 7 AM is 31° and the opposite side to that angle is x.
Using trigonometry, we can solve for x as follows
tan(31°) = 5.55 / x
x = 5.55 / tan(31°)
x = 5.55/0.60086
x = 9.24 meters
Therefore,
Archimedes went to sleep about 9.24 meters away from the rock where its shadow should end when it was 7 AM.
Learn more about Trigonometric ratios at
https://brainly.com/question/25122825
#SPJ1
Solve this inequality 15n<8n-21
Answers
The solution of the inequality 15n>8n-21 is given by, n<-3.
Inequality is a relation between two or more mathematical expression or quantities via unequal signs i.e. greater, less, greater or equal, less or equal, not equal.
Given that the inequality is 15n<8n-21
Solving the inequality we have,
15n<8n-21
15n-8n<8n-21-8n, subtracting from both sides
7n<-21
n<-3, dividing 7 from both sides
So the solution of the given inequality is, n<-3.
To know more about Inequality refer to:
https://brainly.com/question/24372553
#SPJ1
Patrick plays his guitar in a park and earns $3 for each song he plays. Hall plays his guitar at a local coffee shop and earns $9 for each song he plays, but he also has to pay a $110 fee to play at the coffee shop. Determine which equation could be used the find n, the number of songs they will have to play in order to earn the same amount of money.
Answers
Answer:
3n = 9n - 110
Step-by-step explanation:
Let's suppose that Patrick and Hall play n number of songs to earn the same amount of money.
For Patrick, the amount of money he earns is given by:
Money earned by Patrick = 3n
For Hall, the amount of money he earns after paying the $110 fee is given by:
Money earned by Hall = 9n - 110
To find the number of songs they will have to play in order to earn the same amount of money, we need to set these two expressions equal to each other and solve for n:
3n = 9n - 110
Simplifying this equation, we get:
6n = 110
Dividing both sides by 6, we get:
n = 110/6
n = 18.33 (rounded to two decimal places)
Since n represents the number of songs, it cannot be a fractional value. Therefore, we can conclude that they will have to play 18 songs to earn the same amount of money.
Therefore, the equation that could be used to find n, the number of songs they will have to play in order to earn the same amount of money, is:
3n = 9n - 110
Hope this helps!
Quadrilateral ABCD is a square and the length of BD¯¯¯¯¯ is 10 cm.
What is the length of AE¯¯¯¯¯ ?
Enter your answer in the box.
the length of AE¯¯¯¯¯ =
cm
Answers
The length of AE¯¯¯¯¯ is 5√2 cm.
Since quadrilateral ABCD is a square, all four sides are congruent. Let's denote the length of one side as s. Therefore, the length of BD¯¯¯¯¯ is equal to s.
Given that the length of BD¯¯¯¯¯ is 10 cm, we can conclude that s = 10 cm.
Now, we need to find the length of AE¯¯¯¯¯. Looking at the square, AE¯¯¯¯¯ is the diagonal connecting opposite corners.
In a square, the diagonal divides the square into two congruent right triangles. We can use the Pythagorean theorem to find the length of the diagonal.
The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides.
In this case, the diagonal (the hypotenuse) is the same as the side length, s.
Applying the Pythagorean theorem:
s^2 = AE¯¯¯¯¯^2 + AE¯¯¯¯¯^2
10^2 = AE¯¯¯¯¯^2 + AE¯¯¯¯¯^2
100 = 2 * AE¯¯¯¯¯^2
AE¯¯¯¯¯^2 = 50
Taking the square root of both sides:
AE¯¯¯¯¯ = √50
Simplifying the square root:
AE¯¯¯¯¯ = √(25 * 2) = 5√2 cm
for more such questions on quadrilateral
https://brainly.com/question/27991573
#SPJ8
7. Identify the axis of symmetry of the parabola.
y = -1
-8-6-4 P
-2/
X = 1
X = -1
y4
8
y = 1
6-
4-
2+
CO
+
4 68 X
Q

Answers
Answer:
The answer is y=-1 (answer is C).
Which system of equations could be used to find the number of tickets sold before the tournament, x, and the number of tickets sold at the door, y? Remember, 743 tickets were sold, and 75 more tickets were purchased before the tournament than at the door.
Select the correct system based on the scenario.
y = x + 75
y = 75x + 743
y = x + 75
y = x + 743
x + y = 743
x – y = 75
x + y = 743
y – x = 75
Which system of equations could be used to find the number of tickets sold before the tournament, x, and the number of tickets sold at the door, y? Remember, 743 tickets were sold, and 75 more tickets were purchased before the tournament than at the door.
Select the correct system based on the scenario.
y = x + 75
y = 75x + 743
y = x + 75
y = x + 743
x + y = 743
x – y = 75
x + y = 743
y – x = 75
Answers
Answer:
C. x + y = 743
x – y = 75
Step-by-step explanation:
Got it right.
Answer:
C. x + y = 743
x – y = 75
Step-by-step explanation:
I did the test so trust me :)
suppose that 22 inches of wire cost 66 cents. how much will 38 inches of wire cost in cents?
Answers
Answer:
114 cents
Step-by-step explanation:
1. 66÷22=3 cents per inch
2. 3×38=114
3. 114 cents ($1.14) for 38 inches
Please help this is urgent!

Answers
Answer:
Isosceles
Obtuse
Step-by-step explanation:
1) When two sides of a triangle are the same length, the triangle is an isosceles triangle.
2) When one angle of the triangle is greater than 90 degrees, the triangle is an obtuse triangle.
I hope this helps! Have a great day!
Answer:
Isosceles, obtuse
Step-by-step explanation:
There are three types of triangles based on their sides:
Equilateral: a triangle with 3 equal sidesIsosceles: a triangle with 2 equal sidesScalene: a triangle with no equal sidesThis triangle here as sides of 28 cm, 16 cm, and 16 cm
This triangle has two equal sides of 16 cm, indicating it is an isosceles triangleThere are three types of triangles based on their angles:
Acute: when all angles are less than 90° Right: when the triangle has one angle that is 90° Obtuse: when one of the angles is greater than 90°This triangle has angles of 26°, 26°, and 128°
This triangle has one angle that is greater than 90° → 128°, indicating that this is an obtuse trianglePLEASE HELP!!
The scale on a map reads 0.5 inch = 30 miles. If two cities on the map are 5.75 inches apart, find the actual distance
between the cities.
Answers
Answer:
345 miles
Step-by-step explanation:
So we know that 2 cities are 5.75 inches apart on the map and the scale reads for every 0.5 inch its 30 miles. So we can first start of by diving 5.75 by 0.5, since we need to know how many “0.5” inches are in 5.75 inches. You’d get 11.5. Now 11.5 multiply that by 30 which would get you 345 miles.
$2750 is invested at an interest rate of 3.5% APR compounded quarterly. Determine the amount after 7 years. Round your answer to the nearest hundredth.
Answers
Answer:
To determine the amount of the investment after 7 years, we can use the formula:
A = P(1 + r/n)^(nt)
Where:
A = the future value of the investment (the amount after 7 years)
P = the initial principal or investment amount ($2750)
r = the annual interest rate (3.5%)
n = the number of times the interest is compounded per year (quarterly)
t = the number of years the investment is held (7)
First, we convert the annual interest rate to a decimal: 3.5% = 0.035
Then we convert the interest rate to a quarterly rate by dividing by the number of times it is compounded per year: 0.035 / 4 = 0.00875
We can now substitute these values into the formula:
A = $2750(1 + 0.00875)^(4*7)
A = $2750(1.00875)^28
A = $2750(1.3471)
A = $3710.82
So, the amount of the investment after 7 years is $3710.82, rounded to the nearest hundredth.
a bike wheel radius has a radius of 23 inches and a circumference of 144 inches. what is the diameter
Answers
Answer:
Diameter is 11.5 inches
Step-by-step explanation:
Explanation:
Diameter = 2 x radius
And radius = 23 inches
=> D = 2 x 23 = 46 inches
Solve.
log3 (2x + 5) = 3
Enter your answer in the box.
X = ?
Answers
Answer:
x = 11
Step-by-step explanation:
using the rule of logarithms
\(log_{b}\) x = n ⇒ x = \(b^{n}\)
given
\(log_{3}\) (2x + 5) = 3 , then
2x + 5 = 3³ = 27 ( subtract 5 from both sides )
2x = 22 ( divide both sides by 2 )
x = 11
Find the maximum point of -x^2 + 8x + 40
Answers
The required maximum point of the function \($f(x)=-x^2+8x+40$\) is (4,24).
Explain about quadratic equation.A quadratic equation is an algebraic equation with a maximum degree of two. Where a 0, the equation is provided by ax² + bx + c = 0.
According to questionTo find the maximum point of the quadratic function \($f(x)=-x^2+8x+40$\), we can use the formula for the x-coordinate of the vertex, which is given by \(x=-\frac{b}{2a}$\), where a is the coefficient of the \(x^2$\) term and b is the coefficient of the x term.
In this case, a=-1 and b=8, so the x-coordinate of the vertex is:
\($x=-\frac{b}{2a}=-\frac{8}{2(-1)}=4$$\)
To find the y-coordinate of the vertex, we can plug this value of x into the original function:
\($$f(4)=-4^2+8(4)+40=24$$\)
Therefore, the maximum point of the function \($f(x)=-x^2+8x+40$\) is (4,24).
To know more about quadratic equation visit:
brainly.com/question/30098550
#SPJ9
if f(x)=2x2+5 then f(-3)=
Answers
The function f ( x ) = 2 x² + 5 will have the value 23 for f (- 3).
We are given the function:
f ( x ) = 2 x² + 5
We need to find the value of f ( -3 ).
We will do this by substituting the value of x = - 3 in the function and then evaluating the expression.
Putting x = -3 in the function, we get that:
f ( x = - 3 ) = 2 (- 3)² + 5
Solving the square, we get that:
f (- 3) = 2 ( 9 ) + 5
Simplifying the expression, we get that:
f (- 3) = 18 + 5
f (- 3) = 23
Therefore, we get that, the function f ( x ) = 2 x² + 5 will have the value 23 for f (- 3).
Learn more about function here:
https://brainly.com/question/4025726
#SPJ9
Part A: Use the Pythagorean Theorem to derive the standard equation of the circle, with center at (a, b) and a point on the circle at (x, y). Show all necessary math work. (3 points)
Part B: If (a, b) = (5, –2) and c = 10, determine the domain and range of the circle. (4 points)
Part C: Is the point (10, 2) inside the border of the circle if (a, b) = (5, –2) and c = 10? Explain using mathematical evidence. (3 points)

Answers
According to the equation the given all necessary math work are:
\(A: (x -f)^2 +(y -g)^2 = h^2\)
B: domain: [-5, 11]; range: [-9, 7]
C: yes, inside
What is Pythagοras theοrem?The hypοtenuse's square is equal tο the sum οf the squares οf the οther twο sides if a triangle has a straight angle (90 degrees), accοrding tο the Pythagοras theοrem. Keep in mind that BC² = AB² + AC² in the triangle ABC signifies this. Base AB, height AC, and hypοtenuse BC are all used in this equatiοn. The lοngest side οf a right-angled triangle is its hypοtenuse, it shοuld be emphasized.
Part A:
Use οf the Pythagοrean theοrem gets yοu tο the equatiοn fοr a circle in essentially οne step:
sum οf squares οf sides = square οf hypοtenuse
\((x -f)^2 +(y -g)^2 = h^2\) . . . . . . circle cantered οn (f, g) with radius h
Part B:
The circle will be defined fοr values οf x in the dοmain f ± h, and fοr values οf y in the range g ± h.
dοmain: 3 ± 8 = [-5, 11]
range: -1 ±8 = [-9, 7]
Part C:
The distance frοm pοint (10, -4) tο (f, g) is ...
\(h^2 = (10 -3)^2 +(-4 -(-1))^2\)
\(h^2 = 7^2 +(-3)^2 = 49 +9 = 58\)
h = √58 < 8 . . . . the distance tο the pοint is less than h=8.
The pοint is inside the circle.
Learn more about Pythagoras theorem, by the following link
https://brainly.com/question/231802
#SPJ1
Is (1,8), (2,12), (3,16) (4,20) a function?
Answers
Find the missing value using the given information
(4,p), (p,-3), m=5/3
Please help!
Answers
Answer:
(4,2), (1,-3), m=5/3
Step-by-step explanation:
I kinda just used trial and error I guess. Since you find the slope by doing y-y1/x-x1. I did P--3 over 4-p =5/3 and just used logic to see which numbers fit
Ronald is walking at a rate of 3 miles per hour. If he walks for 2 hours and then runs at a rate of 6 miles per hour for another 1 hour, how far did Ronald travel in total?
Answers
Answer:
12Step-by-step explanation:
Ronald's walking speed is 3 miles per hour, and he walks for 2 hours, so he covers 3 * 2 = 6 miles. In the next hour, he runs at a speed of 6 miles per hour, covering an additional 6 miles. Therefore, Ronald traveled a total of 6 + 6 = 12 miles.