What is the quotient of 2,173 ÷ 53
Answers
Answer:
41
Step-by-step explanation:
Related Questions
For the function given, state the starting point for a sample period:
ƒ(t) = −100sin (50t − 20).
plz help
Answers
Use the form a sin ( b x − c ) + d to find the amplitude, period, phase shift, and vertical shift.
Amplitude: 100
Period: π / 25
Phase Shift: 2 /5 ( 2 /5 to the right)
Vertical Shift: 0
A girls typing an essay on her computer she typed 2/5 of a paper of an essay in 1/15 hour all this rate how long in hours would it take her to type a full page
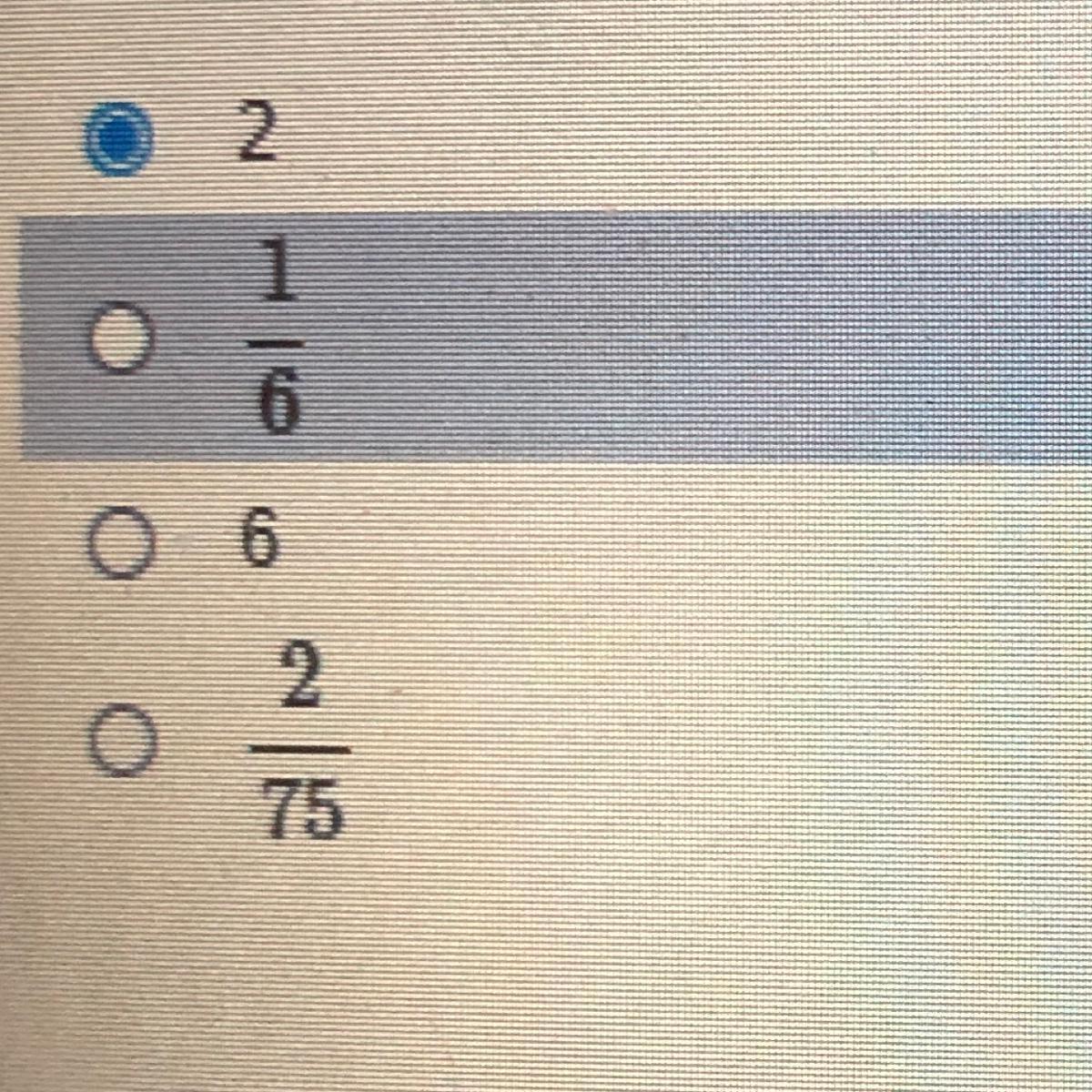
Answers
For a population with µ = 65 and σ = 4, what is the X value corresponding to z = -2.25?
a. X = 74
b. X = 56
c. X = 71
d. X = 60
Answers
The X value corresponding to z = -2.25 is X = 56.
What is z - score?A z score is a statistical indicator that shows how far a raw score is from a distribution's mean. Give the z-score formula. The z-score is calculated using the formula z = (x -μ)/σ.
To find the corresponding X value for a given z-score, we use the formula:
X = µ + (z * σ)
Given µ = 65, σ = 4, and z = -2.25, we can calculate the X value:
X = 65 + (-2.25 * 4)
X = 65 - 9
X = 56
Therefore, the X value corresponding to z = -2.25 is X = 56.
The correct answer is b. X = 56.
Learn more about z-score on:
https://brainly.com/question/15222372
#SPJ4
A scientist is studying the relationship between amiet temerature and the heights of individuals plants. When the ambient temperatures was 25 degree celsius plants reached maximum heights of 4.9 metters and when the ambient temperatures was 30 degrees Celsius plants reached maximum heights of 4.4 metters. What function best captures this relationship where x is temperature, in degrees Celsius and f(x) is plants height in meters
Answers
A function that describes relationship between Amite temperature and the heights of individuals plants is:
f(x) = -0.08x + 4.9
where, x is temperature, in degrees Celsius and f(x) is plants height in meters
In this question, we have been given a scientist is studying the relationship between Amite temperature and the heights of individuals plants.
When the ambient temperatures was 25 degree Celsius plants reached maximum heights of 4.9 meters
and when the ambient temperatures was 30 degrees Celsius plants reached maximum heights of 4.4 meters.
We need to find a function that describes this relationship where x is temperature, in degrees Celsius and f(x) is plants height in meters.
The rate of change in the height of plants.
Consider points (25, 4.9) and (30, 4.4)
r = (4.4 - 4.9) / (30 - 25)
r = -0.4 / 5
r = -0.08
So, a linear function in slope-intercept form would be,
f(x) = -0.08x + b
for x = 25,
2.9 = -0.08(25) + b
b = 2.9 + 2
b = 4.9
so, we get a linear function
f(x) = -0.08x + 4.9
Therefore, a function that describes relationship between Amite temperature and the heights of individuals plants is:
f(x) = -0.08x + 4.9
where, x is temperature, in degrees Celsius and f(x) is plants height in meters
Learn more about the function here:
https://brainly.com/question/28193994
#SPJ1
‼️(15 points)‼️
The aquarium below is 12 in. wide, 36 in. long, and 24 in. tall. It is filled with water, leaving 1 inch of the aquarium empty at the top.
How many cubic feet of water are in the aquarium?
A. 72 ft
OB. 61.5 ft
OC. 6 ft
OD. 5.75 ft?
Answers
Answer:
OC.6 ft hope this helps you
Answer: 6 ft
Step-by-step explanation:
L×w×h 36×12×24=10368in
1 cubic foot = 1728in 10368÷1728=6
(a) A = = (b) A = 2 2 4 1 -2 -2 -7] -4
Answers
By multiplying matrices B and A, we obtain the product BA. Using BA, we can solve the system of equations y + 2z = 7, x - y = 3, and 2x + 3y + 4z = 17.the values of x, y, and z are -1, 2, and 1 respectively
To find the product BA, we multiply matrix B with matrix A. The resulting matrix will have the same number of rows as B and the same number of columns as A. The product BA will be used to solve the given system of equations.
The product BA can be computed by multiplying each row of matrix B by each column of matrix A and summing the results. The resulting matrix will be:
Now, we can use the product BA to solve the system of equations:
-10x - 10y + 6z = 7,
3x - 8y + 2z = 3,
-6x - 16y + 15z = 17.
1 -1 2
2 3 1
0 4 2
We can rewrite this system of equations as:
-10x - 10y + 6z = 7,
3x - 8y + 2z = 3,
-6x - 16y + 15z = 17.
By comparing the coefficients of x, y, and z in the system of equations with the entries in the matrix BA, we can determine the values of x, y, and z.
Solving the system of equations using matrix BA, we get:
x = -1,
y = 2,
z = 1.
Therefore, the values of x, y, and z are -1, 2, and 1 respectively.
Learn more about matrices here
https://brainly.com/question/30646566?referrer=searchResults
#SPJ11
The complete question is:
Given A=
⎣2 2 -4|
|-4 2 -4|
|2 -1 5|
, B=
⎣1 -1 0|
⎢2 3 4|
⎢0 1 2|
, find BA and use this to solve the system of equations y+2z=7, x−y=3, 2x+3y+4z=17.
Solve for x. Rolind to the nearest hundredth.

Answers
cos(51°) = x/7
x = 7 • cos(51)
x = 4.4052 = 4.41
How far away from zero on the y-axis is the point (2, 5)?
A. 2
B. 0
C. 5
D. 1
Answers
the answer is C
Step-by-step explanation:
2 is the x axis and 5 is the y
what is an exponential decay function

Answers
for a random variable x, v(x + 3) = v(x + 6), where v refers to the variance.
Answers
If\(v(X+3) = v(X+6)\), then X has a constant variance.
How to find random variable?If we have a random variable X, then we know that:
\(v(X) = E[(X - μ)^2],\)
where E is the expectation operator and μ is the mean of X.
Using this formula, we can expand v(X+3) and v(X+6) as follows:
\(v(X+3) = E[(X+3 - μ)^2]\\v(X+6) = E[(X+6 - μ)^2]\)
Now we can simplify these expressions:
\(v(X+3) = E[(X - μ + 3)^2]\\= E[(X - μ)^2 + 6(X - μ) + 9]\\= v(X) + 6E[X - μ] + 9v(X+6) \\= E[(X - μ + 6)^2]\\= E[(X - μ)^2 + 12(X - μ) + 36]\\= v(X) + 12E[X - μ] + 36\)
Since v(X+3) = v(X+6), we can equate the two expressions:
\(v(X) + 6E[X - μ] + 9 = v(X) + 12E[X - μ] + 36\\\)
Simplifying this equation yields:
\(6E[X - μ] = 27\\E[X - μ] = 4.5\)
Since the expected value of X minus its mean is 4.5, we can say that the mean of X+3 is 4.5 greater than the mean of X. Similarly, the mean of X+6 is 4.5 greater than the mean of X.
Since the variance is a measure of how spread out the data is from its mean, and the difference in the means of X+3 and X+6 is constant, it follows that the variances of X+3 and X+6 must also be the same.
Therefore, we can conclude that if\(v(X+3) = v(X+6),\) then X has a constant variance.
Learn more about random variable
brainly.com/question/30976827
#SPJ11
Write an equation of the function
g(x) that is the graph of f(x)=|x| , but shifted right 3 units and shifted down 4 units.
Answers
Answer:
g(x) = |x-3| -4
Step-by-step explanation:
to shift right by 3, subtract three from x inside the absolute value.
to shift down by 4, subtract 4 outside of the absolute value.
g(x) = |x-3| -4
Can someone help me please
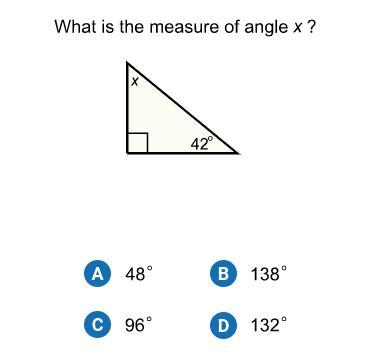
Answers
Answer:
A, 48 degrees
Step-by-step explanation:
180 - 42 - 90 = 48 (all interior angles add up to 48)
Answer:
it’s A
Step-by-step explanation:
it’s a because the right triangle is always 90°.As you can see there is 42° so you subtract to find the missing number.
What is the second step when multiplying mixed numbers?
Answers
5 to the 4th power times 10 to the 4th power
Answers
Answer:
6250000
Step-by-step explanation:
Answer:6250000
Step-by-step explanation:
Suppose that, in an alternate universe, the possible values of m
l
are the integer values including 0 ranging from −l−1 to l+1 (instead of simply −l to +l ). How many orbitals would exist in each of the following subshells? A. p subshell B. d subshell Which atomic orbitals have values of n=3 and I=1 ?
Answers
A. In the alternate universe, the p subshell would have 5 orbitals.
B. In the alternate universe, the d subshell would have 10 orbitals.
In the alternate universe where the possible values of mℓ range from -l-1 to l+1, the number of orbitals in each subshell can be determined.
A. For the p subshell, the value of l is 1. Therefore, the range of mℓ would be -1, 0, and 1. Including the additional values of -2 and 2 from the alternate universe, the total number of orbitals in the p subshell would be 5 (mℓ = -2, -1, 0, 1, 2).
B. For the d subshell, the value of l is 2. In the conventional universe, the range of mℓ would be -2, -1, 0, 1, and 2, resulting in 5 orbitals. However, in the alternate universe, the range would extend to -3 and 3. Including these additional values, the total number of orbitals in the d subshell would be 10 (mℓ = -3, -2, -1, 0, 1, 2, 3).
Therefore, in the alternate universe, the p subshell would have 5 orbitals, and the d subshell would have 10 orbitals.
Learn more about Alternate universe,
brainly.com/question/11181195
#SPJ11
abcd is a square of side length 1. a and c are two opposite vertices. randomly pick a point in abcd. what is the probability that its distance to a and c are both no greater than 1?
Answers
The probability that a randomly chosen point within the square satisfies the condition is approximately 0.215.
Let's label the four corners of the square ABCD in the following way:
A---B
| |
D---C
Assuming that the point is chosen uniformly at random within the square, we can approach this problem using geometry.
Let P be the randomly chosen point within the square. We want to find the probability that the distance from P to A and the distance from P to C are both no greater than 1.
Consider the circle centered at A with radius 1, and the circle centered at C with radius 1. These two circles intersect in two points, which we can label X and Y as shown below:
A---B
| X |
D---C Y
If P is inside the square ABCD and within the intersection of the two circles, then the distance from P to A and the distance from P to C are both no greater than 1. In other words, the region of points that satisfy the condition we're interested in is the intersection of the two circles.
To find the area of this intersection, we can use the formula for the area of a circular segment. Let r be the radius of the circles (in this case, r = 1), and let d be the distance between A and C (which is also the length of the diagonal of the square, so d = sqrt(2)). Then the area of the intersection of the two circles is:
2 * (area of circular segment) - (area of parallelogram)
where the factor of 2 comes from the fact that there are two circular segments (one from each circle). The area of a circular segment with angle theta and radius r is:
(r^2 / 2) * (theta - sin(theta))
where theta is the angle between the two radii that define the segment. In this case, since the two circles intersect at right angles, the angle between the radii is pi/2. So the area of a single circular segment is:
(1/2) * (pi/2 - sin(pi/2))
= (1/2) * (pi/2 - 1)
= (pi - 2) / 4
The area of the parallelogram is just d/2 times the distance from X to Y, which is also d/2. So the area of the parallelogram is (d/2)^2 = 1/2.
Putting everything together, we get:
2 * (area of circular segment) - (area of parallelogram)
= 2 * [(pi - 2) / 4] - 1/2
= (pi - 5) / 4
This is the area of the intersection of the two circles, which is the probability that the randomly chosen point P satisfies the condition we're interested in. So the answer to the problem is:
(pi - 5) / 4
≈ 0.215
Therefore, the probability that a randomly chosen point within the square satisfies the condition is approximately 0.215.
To learn more about parallelogram visit:
https://brainly.com/question/29147156
#SPJ11
Can someone please help me asap ill mark brainlist!!!! and the last answer is 1/10

Answers
Answer:
7/20
Step-by-step explanation:
Answer:
you can give brainlesst to the othere ansere now
Step-by-step explanation:
39) The length of a rectangle is (2x - 1) and the width is (3x2 -5x + 2). Find the area of the rectangle.
Answers
Answer:
(4,-2)
Step-by-step explanation:
Start off by doing everything in the parenthesis which is everyone of them so 2x-1=-2 , your problem then should look like this:
-2(3x2-5x+2) carry the 2 over so multiply the 2 to everything so
(-6x-4+10x+2) add like numbers
10x+-6=4
-4+2=-2
(4,-2)
Please Help ME!!
Identify two or more drawbacks/cons of having one-way streets within a grid street system.
Answers
Answer:
One way streets make it harder to turn into business, also one way streets often are long and they can throw you off your course
Step-by-step explanation:
I hope this helps
How many solutions does the equation 3(4h−1)=−4(3h−5) have?
Answers
Answer:
Step-by-step explanation:
I don’t want more question
I need help no more stress????
A boat could travel 260 km on 65 L of gasoline how much gasoline will it need to go 72 km

Answers
Answer:
18 liters
Step-by-step explanation:
260 km : 65 L
72 km : ? L
Find out how far you can travel on 1 L
65/250 = 4 km
4 km : 1 L
Good. We can use this to find out how much liters we need to travel 72 km.
72 km : ? L :: 4 km : 1 L
72/4 = 18
Alas, we have our answer of 18 liters.
The sum of 3.25 and twice a number is -7.
What is the number? Enter your answer as a decimal.
n =
Answers
Answer: -5.125
Step-by-step explanation:
Let X be the "number."
The sum of 3.25 and twice a number is -7.
3.25 + 2X = -7
2X = -10.25
X = -5.125
Answer:
n = -5.125
Step-by-step explanation: I took the test
The perimeter of a rectangle is 84cm. The length is 12 cm longer than the width. Find the length and width of the rectangle.
Answers
Given:
The perimeter of a rectangle is 84cm.
The length is 12 cm longer than the width.
Required:
We need to find the length and width of the rectangle.
Explanation:
Let l be the length of the rectangle and w be the width of the rectangle.
The length is 12 cm longer than the width.
Add 12 to the width to get the length.
\(l=12+w\)Consider the perimeter of the rectangle formula.
\(P=2(l+w)\)Substitute l=12+w and P =84 in the formula.
\(84=2(12+w+w)\)\(84=24+4w\)Subtract 24 from both sides of the equation.
\(84-24=4w\)\(60=4w\)Divide both sides of the equation by 4.
\(15=w\)Substitute w =15 in the equation l=12+w.
\(l=12+15\)\(l=27\)Final answer:
The length of the rectangle is 27 cm.
The width of the rectangle is 15 cm.
A marathon is 26.2 miles. How many hours would it take a runner whose average speed is 4.25 meters/sec to complete a marathon?
Answers
Given the distance and average speed, the runner will take approximately 2.76 hours to complete the marathon.
How long will it take the runner to complete the marathon?
Speed is simply distance traveled per unit time.
Speed = distance / time
Given the data in the question;
Distance = 26.2 milesSpeed = 4.25m/sTime t = ?First, convert the unit of distance from miles to meter.
Distance = 26.2 miles = ( 26.2 × 1609.34 )m = 42164.708m
Now, plug the values into the equation and solve for time.
Speed = distance / time
4.25m/s = 42164.708m / time
Time = 42164.708m ÷ 4.25m/s
Time = 9921.1077647s
Next, convert to hours,
Time = 9921.1077647 ÷ ( 60 × 60 )
Time = 9921.1077647 ÷ 3600
Time = 2.76 hours
Given the distance and average speed, the runner will take approximately 2.76 hours to complete the marathon.
Learn more about speed here: brainly.com/question/7359669
#SPJ1
Sophie finds some dimes and quarters in her piggy bank. How much money (in dollars) does she have if she has 10 dimes and 12 quarters? How much money (in dollars) does she have if she has x dimes and y quarters?
Answers
Consider the following data drawn independently from normally distributed populations: (You may find it useful to appropriate table: z table or t table)
xˉ1 = −17.1
s1^2 = 8.4
n1=22
xˉ2 = −16.0
s2^2 = 8.7
n2 = 24
a. Construct the 90% confidence interval for the difference between the population means. Assume the population va unknown but equal. (Round final answers to 2 decimal places.)
confidence interval is __ to __
Answers
The 90% confidence interval for the difference in the population means is -2.51 to 0.31
Calculating the 90% confidence interval for the population mean differenceFrom the question, we have the following parameters that can be used in our computation:
xˉ₁ = −17.1
s₁² = 8.4
n₁ = 22
xˉ₂ = −16.0
s₂² = 8.7
n₂ = 24
Calculate the pooled variance using
P = (df₁ * s₁² + df₂ * s₂²)/df
Where
df₁ = 22 - 1 = 21
df₂ = 24 - 1 = 23
df = 22 + 24 - 2 = 44
So, we have
P = (21 * 8.4 + 23 * 8.7)/44
P = 8.56
Also, we have the standard error to be
SE = √(P/n₁ + P/n₂)
So, we have
SE = √(8.56/22 + 8.56/24)
SE = 0.86
The z score at 90% CI is 1.645, and the CI is calculated as
CI = (x₁ - x₂) ± z * SE
So, we have
CI = (-17.1 + 16.0) ± 1.645 * 0.86
This gives
CI = -1.1 ± 1.41
Expand and evaluate
CI = (-2.51, 0.31)
Hence, the confidence interval is -2.51 to 0.31
Read more about confidence interval at
https://brainly.com/question/15712887
#SPJ1
Refer to the equations below: 4x + Ay=4 Ax+y=-2 Find the value of A such that the system of equations, Has no solution 2 Exactly one solution /-2 Infinitely many solutions ? When there is exactly one solution, it is x=2 and y=-2
Answers
The value of A that results in the system of equations having no solution is A ≠ 2.
What is the relationship between a genotype and a phenotype?The given system of equations is 4x + Ay = 4 and Ax + y = -2. To determine the value of A that results in the system having no solution, we can observe that the second equation can be rewritten as y = -Ax - 2.
Since the coefficient of y is not equal to the coefficient of y in the first equation (A ≠ 1), the lines represented by these equations will have different slopes.
Consequently, the lines will never intersect and there will be no solution to the system. Thus, the value of A that satisfies this condition is A = 2.
Learn more about having no solution
brainly.com/question/27978052
#SPJ11
Marissa just bought 100 acres of land. She wants to grow apple, peach, and cherry trees on her land. Color the
model to show how the acres could be distributed for each type of tree. Using your model, complete the table.
Answers
Answer:
Step-by-step explanation:
Robb’s Fruit Farm consists of 100 acres on which three different types of apples grow. On 25 acres, the farm grows Empire apples. Mcintosh apples grow on 30% of the farm.
Triangle HIJ, with vertices H(5,2), I(8,5), and J(3,9), is drawn inside a rectangle, as shown below. x y H I J What is the area, in square units, of triangle HIJ? Answer: � = A= units 2 units 2
Answers
Based on the information provided, the area in square units is for the triangle HIJ.
What is the area of the triangle HIJ?To calculate the area of this triangle we are required to calculate the total area and then subtract the area of the three other triangles.
Total area:
5 units x 9 units = 45 units
Area of the first triangle: 1/2 × b × h
1/2 x 2.5 x 7 = 8.7
Area of the second triangle: 1/2 × b × h
1/2 x 3 x 3= 4.5
Area of the third triangle: 1/2 × b × h
1/2 x 5 x 4= 10
Area of the missing triangle: 45 units - 8.7 units - 4.5 units - 10 units = 21.8 units.
Note: This question is incomplete; below I attach the missing section.
Learn more about the area in https://brainly.com/question/27683633
#SPJ1

HURRYYYYYYY
Fill in the blank with the correct number.
A number is divisible by
divisible by four.
if the last two digits form a number
A) 3
B) 4
C) 6
D) Both 3 and 4
Answers
Answer:
D
Step-by-step explanation:
the answer is D: Both 3 and 4