What is the slope of (-4,4) and (-1,-3) please
Answers
The slope of the line is 7/5
What is a Slope of a Staright Line?
A slope of a line is defined in mathematics as the change in y coordinate with regard to the change in x coordinate. The net change in y-coordinate is denoted by y, whereas the net change in x-coordinate is denoted by Δx. As a result, the change in y-coordinate in relation to the change in x-coordinate is given by,
m = difference in y/difference in x = Δy/Δx
Where "m" represents the slope of a line.
Solution:
As mentioned above;
m = difference in y/difference in x = Δy/Δx
So, Slope of the line passing through (-4,4) and (-1,-3) is
Slope = -3 - 4 / -1 - 4
Slope = -7 / -5 = 7/5
The slope of the line is 7/5
To learn more about Slope of a Straight Line from the given link:
brainly.com/question/3493733
#SPJ1
Related Questions
Mr. Holloway went to Comic-Con for the new Marvel Legends exhibit. He is trying to figure out how many
booths he traveled to per hour. He LOVED wandering through Spider-Man's web, holding Captain America's
shield, practicing his repulsor beam tech with Iron Man, and observing all of the Infinity Stones! Let's help him
remember! Before he started keeping track he had already visited 5 booths. Because of the lines, he is only
able to make it to 3 booths per hour. If the exhibit was only open for 5 more hours, how many total booths did
he visit?
a. Write an equation of the line in slope-intercept form.
b. How many total booths did he visit?
SHARV
Answers
Answer:
Mr. Holloway visited 20 booths in total.
Step-by-step explanation:
Mr. Holloway has already visited 5 booths for the new Marvel Legends exhibit.
a.
Due to the lines, he can only make it to 3 booths per hour. Let's call h the number of hours and b the total number of booths he visits.
The model consists of a fixed amount (the booths already visited), and a variable amount (the booths he visits per hour), thus the function is constructed as:
b = 5 + 3h
b.
Now we find the total booths he visited for h=5 hours:
b = 5 + 3*5
b = 5 + 15
b = 20
Mr. Holloway visited 20 booths in total.
9. The Super Vision cable TV/Internet/phone provider advertises a flat $100 monthly fee for all
three services for a new customer. The rate is guaranteed for 5 years. Cable Zone normally
charges $46 for monthly home phone service, $36 for monthly Internet service, and $56 for
monthly cable television.
a. How much could a customer save during the first year by switching from Cable Zone to
Super Vision?
b. Super Vision raises the rates 23% after a new customer's first year, how much will a customer
who switched from Super Vision save in the second year?
c. If Super Vision raises the rates 18% for the third year compared to the second year, which
company is cheaper for the third year?
Answers
a. $456 would be the amount a customer could save during the first year by switching from Cable Zone to Super Vision.
b. Super Vision raises the rates 23% after a new customer's first year, a customer who switched from Super Vision save $180 in the second year.
c. Super Vision raises the rates 18% for the third year compared to the second year, for the third year, Cable Zone would be cheaper.
a. To calculate how much a customer could save during the first year by switching from Cable Zone to Super Vision, we need to compare the costs of the two providers.
Cable Zone charges $46 for monthly home phone service, $36 for monthly Internet service, and $56 for monthly cable television. Therefore, the total cost per month with Cable Zone is:
$46 (home phone) + $36 (Internet) + $56 (cable television) = $138
Super Vision, on the other hand, offers all three services for a flat $100 monthly fee. So, the customer would save:
$138 (Cable Zone cost) - $100 (Super Vision cost) = $38 per month
Therefore, during the first year, the customer could save:
$38 (monthly savings) * 12 (number of months) = $456
b. After the first year, Super Vision raises the rates by 23%. The new monthly fee would be:
$100 (original fee) + 23% (rate increase) * $100 (original fee) = $123
To calculate the savings in the second year, we need to compare the new Super Vision fee to the cost with Cable Zone:
$138 (Cable Zone cost) - $123 (Super Vision cost) = $15 per month
Therefore, in the second year, the customer would save:
$15 (monthly savings) * 12 (number of months) = $180
c. If Super Vision raises the rates by 18% for the third year compared to the second year, we need to calculate the new monthly fee. The new Super Vision fee would be:
$123 (second-year fee) + 18% (rate increase) * $123 (second-year fee) = $145.14
To determine which company is cheaper for the third year, we compare the new Super Vision fee to the cost with Cable Zone:
$138 (Cable Zone cost) - $145.14 (Super Vision cost) = -$7.14
In this case, the Super Vision cost is higher than the Cable Zone cost by $7.14 per month. Therefore, for the third year, Cable Zone would be cheaper.
Overall, during the three-year period, the customer would save a total of $456 (first year) + $180 (second year) = $636 by switching to Super Vision.
For more such information on: rates
https://brainly.com/question/25720319
#SPJ8
A cylindrical pottery vase has a diameter of 4.3 inches and a height of 11 inches. What is the surface area of the vase? Use the formula SA = B + Ph, since the vase has a bottom but no top. Use 3.14 for π
and round to the nearest tenth of a square inch.
Answers
The surface area of the cylindrical pottery vase is 177.55 in².
Given that a cylindrical pottery vase has a diameter of 4.3 inches and a height of 11 inches, we need to find the surface area of the vase,
SA of a cylinder = 2π×radius(h+r)
= 2×3.14×2.15(2.15+11)
= 177.55 in²
Hence, the surface area of the cylindrical pottery vase is 177.55 in².
Learn more about cylinder click;
https://brainly.com/question/16134180
#SPJ1
Aisha organized her books for 1/6 hour and her coin collection for 3/7 hour.
What is the best estimate for the total time Aisha spent organizing?
Drag and drop an answer into each box to correctly complete the sentences.
1/6 hour is closest to(0 hours, 1/2 hour, 1 hour, 1 1/2 hour, 2 hours) area. 3/7 hour is closest to(0 hours, 1/2 hour, 1 hour, 1 1/2 hour, 2 hours)area. Therefore, the best estimate for the total time Aisha spent organizing is close to(0 hours, 1/2 hour, 1 hour, 1 1/2 hour, 2 hours)area.
Answers
Answer:
1/2 hour
Step-by-step explanation:
1/6 is closest to 0 hours
3/7 is closest to 1/2 hour
Answer is 1/2 hour
what is the absolute value of -0.575
Answers
Answer:
hQIwgqhioiojhwvjia I VJILAija IOJA iojiao JIOA JIOJIA JIoj ijioJ Jjio ji jijioJI JIioj jio
Step-by-step explanation:
ADD 34
Which of the following quotients are equal to -2/7 select all that apply please help ):
Answers
Based on the quotient given of -2/7, the quotients that are equal to it include:
-2/7-4/14-8/28Which quotients are equal?As there are no options provided, I will give a general answer to explain the concept.
When looking for quotients that are equal to a number, you need to look for quotients that when simplified, lead to the quotient it is to equal.
The quotient in this case which is -2/7 can be equal to quotients like:
= -4/14 and -8/28
When these are reduced to their simplest, they take the form -2/7.
Find out more on equal quotients at https://brainly.com/question/20459154
#SPJ1
Alta dove 9 meters below the ocean’s surface. She then dove 15 meters deeper. She then rose 19 and one-fourth meters. What was her position in relation to the surface of the water?
Answers
Answer: -4 3/4
Step-by-step explanation:
Above is the answer if you have a drop down menu, because I have a drop down menu.

Answer:
B
Step-by-step explanation:
i got it right
In 1995, wolves were introduced into Yellowstone Park.
The function `w\left(x\right)=14\cdot1.08^{x}` models the number of wolves, `w`, in the years since 1995, `x`.
By what percent does the number of wolves change each year?
Answers
In this manner, the number of wolves changes by around 8 percentage 8% each year based on the given work.
Percent calculation.
To determine the percentage change within the number of wolves each year, we ought to look at the development rate of the work w(x) = 14 * 1.08^x.
The development rate in this case is given by the example of 1.08, which speaks to the figure by which the number of wolves increments each year. In this work, the coefficient 1.08 speaks to a development rate of 8% per year.
To calculate the percentage change, we subtract 1 from the growth rate and increase by 100 to change over it to a rate:
Percentage change = (1.08 - 1) * 100 = 0.08 * 100 = 8%.
In this manner, the number of wolves changes by around 8 percentage 8% each year based on the given work.
Learn more about percentage below.
https://brainly.com/question/24304697
#SPJ4
2.145 is divisible by which numbers
2
6
5
3
Answers
Answer:
3 and 5 if "." marks thousands2, 3, 5, 6 if "." is a decimal pointStep-by-step explanation:
The number 2145 is not even, so will not be divisible by 2 or 6. It ends in 5 so is divisible by 5. Its sum of digits is 12, which is divisible by 3, so the number is divisible by 3.
2145 is divisible by 3 and 5.
2.145 is divisible by all of these numbers:
2.145/2 = 1.0725
2.145/6 = 0.3575
2.145/5 = 0.429
2.145/3 = 0.715
_____
Here, we take the mixed number to be divisible if the decimal representation of the quotient is a terminating decimal fraction.
Multiplication equation-
X
Groups
10. Write a multiplication equation for each one.
a) 2+2+
2+2 + 2 =
b.) 5+5+5+5+5=
c.) 4 groups of 3 =
Draw a picture of 4 groups of 3
------->
--->
->
X
X
X
=
Answers
we get the the multiplication equations are 2 + 2 + 2 + 2 + 2 = 2 × 5, 5 + 5 + 5 + 5 + 5 = 5 × 5 and 4 groups of 3 = 3 × 4.
We are given some expressions and we need to find the multiplication equation for each one.
a) 2 + 2 + 2 + 2 + 2 will be
Since, 2 is repeating 5 times, we get that:
multiplication equation will be:
2 + 2 + 2 + 2 + 2 = 2 × 5
b) 5 + 5 + 5 + 5 + 5 will be
Since, 5 is repeating 5 times, we get that:
multiplication equation will be:
5 + 5 + 5 + 5 + 5 = 5 × 5
c ) 4 groups of 3 will be
Since, 3 is repeating 4 times, we get that:
multiplication equation will be:
4 groups of 3 = 3 × 4
Therefore, we get the the multiplication equations are 2 + 2 + 2 + 2 + 2 = 2 × 5, 5 + 5 + 5 + 5 + 5 = 5 × 5 and 4 groups of 3 = 3 × 4.
Learn more about multiplication equations here:
https://brainly.com/question/10873737
#SPJ9

What is the length of the hypotenuse of the triangle below?
45°
h
5V2
45°
90°
52

Answers
The length of the hypotenuse of the triangle whose other two sides are of the length 5√2 units is given by: Option B: 10 units.
What is Pythagoras Theorem?If ABC is a triangle with AC as the hypotenuse and angle B with 90 degrees then we have:
\(|AC|^2 = |AB|^2 + |BC|^2\)
where |AB| = length of line segment AB. (AB and BC are rest of the two sides of that triangle ABC, AC being the hypotenuse).
For this case, consider the figure attached below.
Then, we are given the facts that:
Triangle ABC is a right angled triangle with right angle at vertex BThe lengths of non-hypotenuse sides AB and BC are 5√2 unitsThe length of the hypotenuse AC, denoted by h is to be found.Using the Pythagoras theorem, we get:
\(|AC|^2 = |AB|^2 + |BC|^2\\\\h^2 = (5\sqrt{2})^2 + (5\sqrt{2})^2 \\\\h^2 = 2(5\sqrt{2}))^2\)
Taking root, we get:
\(h = \sqrt{2 (5\sqrt{2})^2}\) (only positive root since h is denoting length, which is a non-negative quantity).
Thus, we get:
\(h = \sqrt{2 (5\sqrt{2})^2} = \sqrt{(5\sqrt{2})^2} \times \sqrt{2} = (5\sqrt{2}) \times \sqrt{2} = 5 \times (\sqrt{2})^2 = 5 \times 2 \\\\h= 10 \: \rm units\)
(square cancelled the square root).
Thus, the length of the hypotenuse of the triangle whose other two sides are of the length 5√2 units is given by: Option B: 10 units.
Learn more about Pythagoras theorem here:
https://brainly.com/question/12105522

Answer:
10 units.
Step-by-step explanation:
just took the quiz
If Margo walks 1/4 mile in 1/12 of an hour, what is her unit rate
Answers
To find the unit rate, we need to determine how much distance Margo covers in one unit of time. We can do this by dividing the distance by the time.
Distance = 1/4 mile
Time = 1/12 hour
Unit rate = Distance ÷ Time
Unit rate = (1/4 mile) ÷ (1/12 hour)
We can simplify this division by multiplying both the numerator and denominator by the least common multiple of 4 and 12, which is 12.
Unit rate = (1/4 mile) ÷ (1/12 hour) x (12/12)
Unit rate = (3/4 mile) ÷ 1 hour
Unit rate = 3/4 mile per hour
Therefore, Margo's unit rate is 3/4 mile per hour. This means that she can cover a distance of 3/4 mile in one hour of walking.
Answer:
3mph
Step-by-step explanation:
1/12 of an hour will be 5 min. In 5 min she can walk 1/4 mile then in one hour she can walk 1/4 x 12. This means her rate will be 3 miles per hour.
60/12 = 5
12 x 1/4 = 12/4 = 3
What is the slope of the line that passes through the points (1,−1)(1,−1) and (−8,−7)(−8,−7)? Write your answer in simplest form.
Answers
Answer: 62314667
Step-by-step explanation: because numbers dontlie
what is the property of 3x(5x7)=(3x5)7
Answers
The property you are referring to is called the associative property of multiplication. According to this property, when multiplying three numbers, the grouping of the numbers does not affect the result. In other words, you can change the grouping of the factors without changing the product.
In the equation you provided: 3x(5x7) = (3x5)7
The associative property allows us to group the factors in different ways without changing the result. So, whether we multiply 5 and 7 first, or multiply 3 and 5 first, the final product will be the same.
math project : I need an interesting project idea for mathematics that can relate 3 different topics, I should write a full research paper related on the topic this are some examples related to the project
You must state a question that you would like to answer. This must be a specific question within your topic and should be explored thoroughly to create a complete paper.
Examples:
(i) How can we use Mathematical/Calculus-based tools to study the spread of COVID-19?
(ii) Designing a new Mathematical/Calculus-based model to analyze the spread of COVID-19
(iii) How many entrances should there be at Expo to accommodate all visitors?
(iv) How much water does the UAE need in order to sustain its ever changing population? (i.e. comparing water usage vs. water production)
Literature review:
You must show using multiple references and sources of the current literature on your given topic. This does NOT imply that information is simply copied from the internet but rather you must present a comprehensive review and summary of the latest research on your topic. It is suggested that you chose a specific aspect of your topic in order to include all required elements.
Examples:
(i) Review of the existing Mathematical/Calculus-based models used to analyze the spread of COVID-19
(ii) Review of existing Mathematical/Calculus-based models and calculations regarding risk insurance.
Answers
Answer:
Here's an interesting project idea for mathematics that can relate three different topics:
Topic 1: Fractals
Topic 2: Chaos Theory
Topic 3: Differential Equations
Research Question: Can fractals be used to model chaotic systems described by differential equations?
In this project, you can explore the concept of fractals and their applications in modeling complex systems. You can also delve into chaos theory and differential equations to understand how they are used to describe chaotic systems. By combining these three topics, you can investigate whether fractals can provide a better understanding of chaotic systems by modeling them more accurately.
Your research paper can cover the following areas:
Introduction: Provide an overview of fractals, chaos theory, and differential equations, and explain their relevance to the research question.
Fractals: Discuss the properties of fractals and how they can be used to model complex systems. Provide examples of fractals in nature and technology.
Chaos Theory: Explain the concept of chaos and how it is described by differential equations. Discuss the importance of chaos theory in understanding complex systems.
Differential Equations: Provide an overview of differential equations and their applications in physics, engineering, and other fields. Explain how differential equations are used to model chaotic systems.
Combining the three topics: Explain how fractals can be used to model chaotic systems described by differential equations. Provide examples of fractals used in modeling chaotic systems and compare the results to traditional methods.
Conclusion: Summarize the findings of your research and discuss the implications of using fractals to model chaotic systems.
Overall, this project can be a challenging and rewarding exploration of the interplay between three different mathematical topics.
Step-by-step explanation:
Question
20 pts
There are 600 6th grade students who attend Falcon Cove Middle School. 17% of them
believe that Mr. Too Much should be fired for being the silliest teacher they have ever known.
How many 6th graders at Falcon Cove believe Mr. Too Much should be fired?
6th graders at Falcon Cove believe Mr. Too Much should be fired.
Question 2
20 pt
Answers
Answer:
u can ask the tutor and he or she will help u in real time and explain
A toy rocket is shot vertically into the air from a launching pad 7 feet above the ground with an initial velocity of 40 feet per second. The height h, in feet, of the rocket above the ground at t seconds after launch is given by the function h(t) = -16t²+40t+7. How long will it take the rocket to reach its maximum height? What is the maximum height?
The rocket reaches its maximum height at ___ second(s) after launch.
(Simplify your answer.)

Answers
The rocket reaches its maximum height at 1.25 second(s) after launch
The maximum height reached by the object is 32 feet.
Time to reach the maximum heightThe function is given as
h(t) = -16t² + 40t + 7
Differentiate the above function
So, we have the following representation
h'(t) = -32t + 40
Set to 0
-32t + 40 = 0
So, we have
32t = 40
Divide by 32
t = 1.25
Hence, the time is 1.25 seconds
The maximum heightIn (a), we have
t = 1.25
Substitute t = 1.25 in h(t) = -16t² + 40t + 7
h(1.25) = -16(1.25)² + 40(1.25) + 7
Evaluate
h(1.25) = 32
Hence, the maximum height is 32 feet
Read more about height functions at
https://brainly.com/question/10837575
#SPJ1
(1 point) Find f'(1) if 6x (f(x))^4 +9x^3 f(x) = 78 and f(1) = -2

Answers
Answer:
42
Step-by-step explanation:
\(6x (f(x))^{4}+9 x^{3} f(x)=78\\6x (f(1))^{4}+9 x^{3} f(1)=78\\6x(-2)^{4}+9 x^{3} (-2)=78\\f(x) = 6x(16)-18 x^{3}=78\\f'(x)=96-54x\\for x=1: f'(1)=96-54(1)=42\)
Please help me quick

Answers
The product of the ages 2 years from today is 924
System of equationLet the ages of the three cousins be x, y and z. If the product of their ages is 1716, hence;
xyz = 1716
If the product of their ages last year is 1320, then;
(x-1)(y-1)(z-1) = 1320
Two years ago, the product of their ages will be;
(x-2)(y-2)(z-2) = 1320- (1716-1320)
(x-2)(y-2)(z-2) = 1320-396
(x-2)(y-2)(z-2) =924
Hence the product of the ages 2 years from today is 924
Learn more on system of equation here: https://brainly.com/question/25976025
#SPJ1
What is the domain of the equation?


Answers
The domain of the equation include the following: D. all real numbers.
What is a domain?In Mathematics and Geometry, a domain refers to the set of all real numbers (x-values) for which a particular function (equation) is defined.
How to identify the domain any graph?In Mathematics and Geometry, the horizontal portion of any graph is used to represent all domain values and they are both read and written from smaller to larger numerical values, which simply means from the left of any graph to the right.
By critically observing the graph shown in the image attached above, we can reasonably and logically deduce the following domain and range:
Domain = [-∞, ∞] or all real numbers.
Range = [-4, ∞}
Read more on domain here: brainly.com/question/9765637
#SPJ1
150 into the ratio 4:11
Answers
9514 1404 393
Answer:
40 : 110
Step-by-step explanation:
There are a number of ways you can go at this. One of my favorite is to consider the value of a "ratio unit." Here, a total of 4+11 = 15 "ratio units" represent the total to be divided: 150. So the value of each one is ...
150/15 = 10
Then the division is ...
4 : 11 = 10·4 : 10·11 = 40 : 110
_____
Alternate solution
Let x represent the larger share. Then the ratio is ...
(150 -x) : x = 4 : 11
Cross-multiplying gives ...
11(150 -x) = 4x
1650 = 15x . . . . . add 11x, simplify
110 = x . . . . . . . . . divide by 15; the larger share
150-x = 150-110 = 40 . . . . . . the smaller share
The division is 40 : 110.
The animals at a safari park include camels,
kangaroos and meerkats.
There are 12 more kangaroos than there are
camels.
There are 3 times as many meerkats as there
are camels.
There are the same number of kangaroos as
there are meerkats.
How many camels are there at the safari park?
Answers
m = 3c
k = m
Equating the RHS of the first two equations gives
3c = c + 12
2c = 12
c = 6
There are 6 camels
I=$60, P=$300, t=2 years
What is the rate?
Answers
Answer:
i dont know to be honest
Step-by-step explanation: hi
Answers please answer it and correct correct answer will get brainlest and please answer the rate and unit rate ? :))
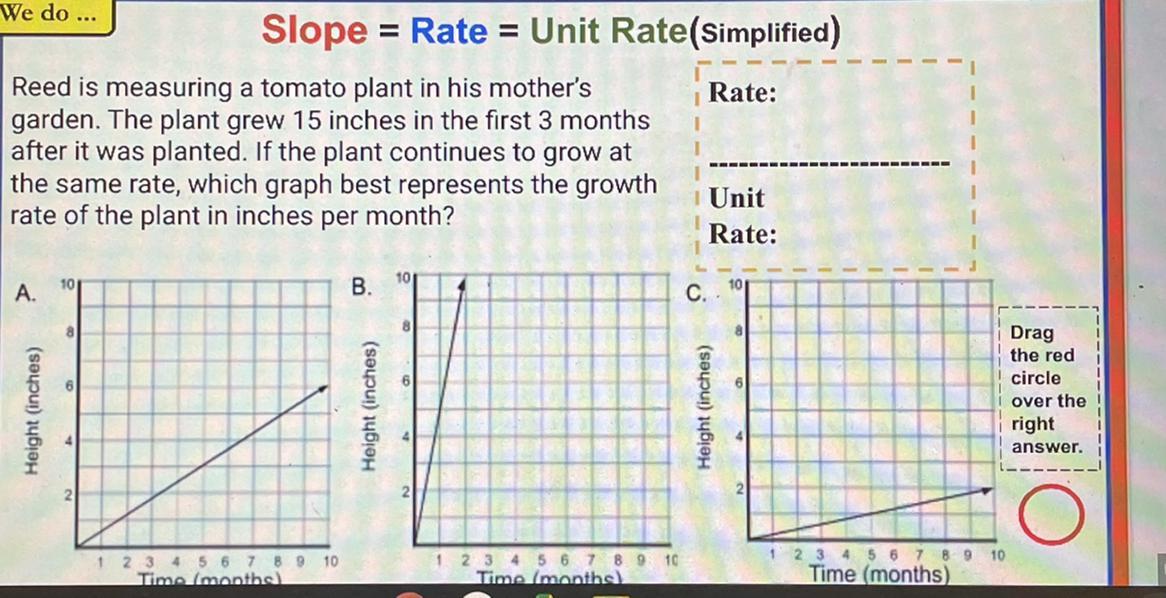
Answers
Question
A watermelon is assumed to be spherical in shape while it is growing. Its mass, M kg, and radius, rcm, are related by the formula M = kr³, where k is a constant. It is also assumed that the radius is increasing at a constant rate of 0.1 centimetres per day. On a particular day the radius is 10 cm and
the mass is 3.2 kg. Find the value of k and the rate at which the mass is increasing on this day.
Answers
Thus, the mass is increasing at a rate of 0.15625 kg per hour, and the mass on this day is 4.5 kg.
Let's consider a general formula for finding the rate of increase:Rate of increase = k x original valueHere, k is a constant that represents the rate of increase per unit of time, and the original value is the initial value of the quantity being measured.
For example, if the original value is 3.2 kg and the rate of increase is 0.5 kg per hour, we can use the formula to calculate the mass at any time t as follows: Mass at
time t = 3.2 + (0.5 x t)
where t is the time elapsed in hours.In order to find k, we need to know the rate of increase and the original value.
Once we have these values, we can rearrange the formula to solve for
k:k = rate of increase / original value
For example, if the mass is increasing at a rate of 0.5 kg per hour and the original value is 3.2 kg, we can calculate k as follows:
k = 0.5 / 3.2k = 0.15625
To find the rate of increase on a specific day, we need to know how much time has elapsed since the original value was measured. Once we have this information, we can plug it into the formula we derived earlier:Mass at time t = 3.2 + (k x t)For example, if 8 hours have elapsed since the original value was measured, we can calculate the mass on that day as follows:
Mass at time t = 3.2 + (0.15625 x 8)
Mass at time t = 4.5 kg
For such more question on original value
https://brainly.com/question/3796282
#SPJ8
Find an equivalent ratio for the ratio 4 : 5.
Answers
simplify 13¹/3+2¹/3-10/2
Answers
The simplified form of 13¹/3 + 2¹/3 - 10/2 is a fraction 64/6 that can be simplified by dividing both the numerator and denominator by their greatest common divisor, which is 2 the final answer is 32/3.
Given
13¹/3+2¹/3-10/2
Required simplified it =?
First, we have simplified both constants separately
13¹/3 = (3 * 13 + 1) / 3 = 40/3
2¹/3 = (3 * 2 + 1) / 3 = 7/3
now the expression become = 40/3 + 7/3 - 10/2
now taking LCM of 3 and 2 which is 6.
= 80/6 + 14/6 - 30/6
now we have to simplify this fraction by dividing by 2 = 64/6
Therefore, the simplified form of 13¹/3 + 2¹/3 - 10/2 is 32/3.
Learn more about Simplification here:
https://brainly.com/question/23509407
#SPJ1
Find the area of the region bounded by the graphs of the following equations.y=5x+6,y=0,x=3andx=8.
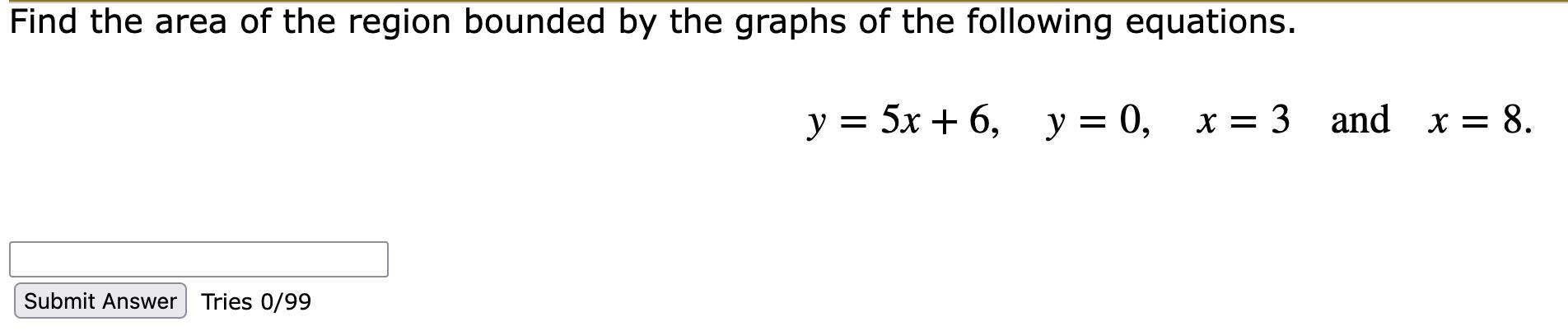
Answers
Given the equations
y=5x+6,
y=0,
x=3and
x=8
we can build the region
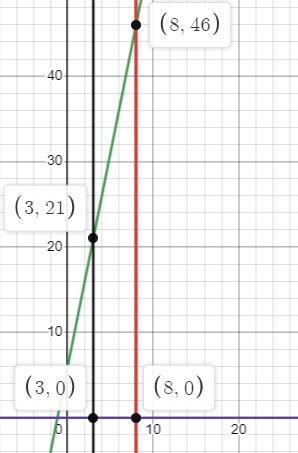
the area is given by the defined integral
\(\int _3^8\:5x+6\)\(\frac{5x^2}{2}+6x|^8_{3^}\)\(\frac{5(8)^2}{2}+6(8)-\frac{5(3)^2}{2}-6(3)\)\(167.5\)Area= 167.5 units^2
For what values of a and b is x^64 + ax^b +25 a perfect square for all integer values of x?
Answers
For the expression \(x^64 + ax^b + 25\) to be a perfect square for all integer values of x, b must be 64, and a must be a perfect square, written as a = \(y^2.\)
To determine the values of a and b such that the expression\(x^64 + ax^b\) + 25 is a perfect square for all integer values of x, we need to analyze the properties of perfect squares.
A perfect square is an expression that can be written as the square of another expression. In this case, we want the given expression to be in the form of\((x^n)^2,\) where n is an even integer.
Let's examine the given expression: \(x^64 + ax^b\) + 25
For it to be a perfect square, the quadratic term \(ax^b\)must have the same exponent as the leading term\(x^6^4.\) This means b must be equal to 64.
So we have:\(x^64 + ax^64 + 25\)
Now, we can rewrite this as:\((x^32)^2 + 2(x^32) (\sqrt{a}) + (\sqrt{25})^2\)
By comparing this with the standard form of a perfect square, (\(x^n +\sqrt{k} )^2\), we can deduce that √a must be equal to x^32 and \(\sqrt{25}\) must be equal to \(\sqrt{k.}\)
Therefore, we have: \(\sqrt{a} = x^3^2\)and\(\sqrt{25} = \sqrt{k}\)
From the second equation, we know that k = 25.
Now, substituting the value of k back into the first equation, we have: \(\sqrt{a} = x^3^2\)
To satisfy this equation for all integer values of x, a must be a perfect square. Therefore, we can express a as a =\(y^2\), where y is an integer.
For more such information on: expression
https://brainly.com/question/1859113
#SPJ8
Members of a lacrosse team raised $1396.75 to go to a tournament. They rented a bus for $850.50 and budgeted $28.75 per player for meals. Determine the number of players the team can bring to the tournament.
Answers
Answer:
19 players
Step-by-step explanation:
If the team raises $1396.75 and the bus costed $850.50 then the remaining budget is = 546.75
If each meal is $28.75 then you could buy 19 meals for 19 players to take to the tournament.