Answers
Related Questions
Who can give me this answer

Answers
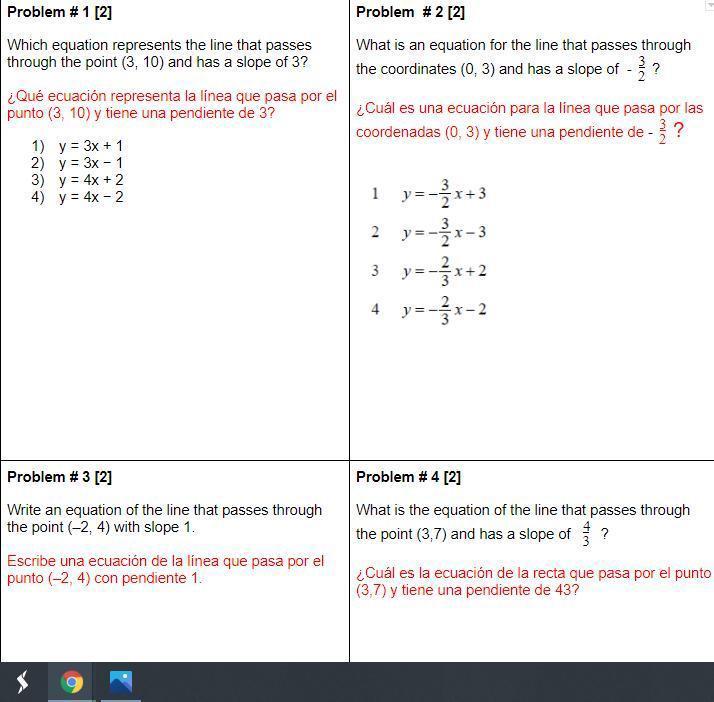
1) Which equation represents the line that passes through the point (3, 10) and has a slope of 3?
2) What is an equation for the line that passes through the coordinates (0, 3) and has a slope of -3/2?
3) Write an equation of the line that passes through the point (–2, 4) with slope 1.
4) What is the equation of the line that passes through the point (3,7) and has a slope of 4/3?
Answers
hello
frrom the question given, we have the value of slope and x,y coordinates
slope = 3
x-axis = 3
y-axis = 10
the standard equation of a line is given as
\(\begin{gathered} y=mx+c \\ m=\text{slope} \end{gathered}\)let's input the values and solve the question
\(\begin{gathered} y=mx+c \\ 10=3(3)+c \\ 10=9_{}+c \\ c=10-9 \\ c=1 \end{gathered}\)NB: c is equals to the intercept
let write out the equation now
\(y=3x+1\)from the calculation above, the equation of line is given as y = 3x +1
If f(1)=7, f(5)=-3, f(11)=-9, g(7)=11, g(-3)=6 and g(-9)=1, then find g(f(11))
Answers
Answer:
1
Step-by-step explanation:
g(f(11))
It says in the problem that f(11) = -9
So:
g(-9)
It says again in the problem that g(-9) = 1
So the answer is 1
Find the angle on the unit circle

Answers
The angle on the unit circle is solved to be
56.01 degrees (to the nearest tenth)
How to find the angleTo find the angle of the terminal side through the given point on the unit circle, we can use the inverse trigonometric functions.
given that P = ((√5)/4, (√11)/4)
θ = arctan ((√11)/4 / (√5)/4)
θ = arctan((√11)/(√5))
θ ≈ 56.01 degrees
hence to the nearest tenth of a degree, the angle of the terminal side through the point P = ((√5)/4, (√11)/4) on the unit circle is approximately 56.01 degrees.
Learn more about unit circle at
https://brainly.com/question/30403151
#SPJ1
Only 40% of people between the ages of 18 and 24 read a daily
newspaper. Write the percent as a fraction in simplest form.
Answers
Answer:
2/5
Step-by-step explanation:
40% = 40/100 = 4/10 = 2/5
Answer:
2/5
Step-by-step explanation:
40%/100% =2/5
you just take the 40% and divide with one hundred %
Find probabilities using combinations and permutations. Emir is handing out 10 invitations to his New Year’s Eve party, 4 of which are printed on blue paper. If Emir randomly hands out 5 invitations before lunch, what is the probability that exactly 2 of the chosen invitations to are printed on blue paper? Write your answer as a decimal rounded to four decimal places.
Answers
We have got 10 invitations, 4 are i blue paper, so 6 are not in blue paper.
To find the probability, we will calculate how many combinations are there and how many combination in which exactly 2 out of 5 of the invitations are blue.
The total combinations of the 5 are just 10! over 5!:
\(T=\frac{10!}{5!}=10\cdot9\cdot8\cdot7\cdot6\)The combinations of ecatly 2 blue starts with 4*3/2!, becase initially we have 4 to choose from but the second we have one less. Now we multiply by the same for the non blue, so 6*5*4/3!, and we get:
\(B=\frac{4\cdot3}{2\cdot1}\cdot\frac{6\cdot5\cdot4}{3\cdot2\cdot1}=2\cdot3\cdot5\cdot4\)The probability is the combinations of the event we want, B, divided by the total combinations, T:
\(\frac{B}{T}=\frac{2\cdot3\cdot5\cdot4}{10\cdot9\cdot8\cdot7\cdot6}=\frac{5\cdot4}{10\cdot9\cdot8\cdot7}=\frac{4}{5\cdot9\cdot8\cdot7}=\frac{1}{2\cdot9\cdot2\cdot7}=\frac{1}{252}=0.003968\ldots\approx0.0040\)So, the probability that exactly 2 of the choosen invitations are printed in blue is 0.0040.
Need answer to this question please don’t understand it

Answers
we have to do alot for this
so first we gotta change 12.3 into a mixed fraction
n = 5 so 5 ÷ 12.3
Ned's Corporation's outstanding bonds have a $1,000 par value, a 4% semi-annual coupon rate, 13 years remaining until maturity,
and a 3% yield to maturity (YTM). What is the price of these bonds?
(A) $899.39
B) $902.00
C) $1,104.65
D) $1,106.99
E $1,213.99
Answers
With the given compound interest, Bond Price = $899.39 i.e. A.
What is Compound interest?
Compound interest is a type of interest that is calculated on both the principal amount and the accumulated interest from previous periods. In other words, it is interest that is earned on interest also.
Now,
To calculate the price of the bonds, we need to use the following formula:
Bond Price = (Coupon Payment / (1 + YTM/2)ⁿ) + (Coupon Payment / (1 + YTM/2)ⁿ⁺¹) + ... + (Coupon Payment + Par Value / (1 + YTM/2)ⁿ*²)
Where:
Coupon Payment = (Coupon Rate x Par Value) / 2
YTM = Yield to Maturity
n = Number of Semi-Annual Periods Until Maturity
Using the information given in the question, we can calculate the coupon payment as:
Coupon Payment = (4% x $1,000) / 2 = $20
We can also calculate the number of semi-annual periods until maturity as:
n = 13 x 2 = 26
Now,
Bond Price = ($20 / (1 + 3%/2)¹) + ($20 / (1 + 3%/2)²) + ... + ($20 + $1,000 / (1 + 3%/2)²⁶)
Bond Price = $899.39
Therefore, the correct answer is (A) $899.39.
To know more about Compound Interest visit the link
brainly.com/question/14295570
#SPJ1
Find the surface area of each solid figure

Answers
Answer:
Step-by-step explanation:

Order the following numbers from least to greatest.
64 cubicle root 18 cubicle root 4.2

Answers
Help please TYSM IF YOU DO!

Answers
Answer:
I think it is mean
Step-by-step explanation:
because mean would be the average of the scores
Answer: The mean
Step-by-step explanation:
The mean will show the average of the teams scores.
What is the domain and range of the function shown on the graph below

Answers
Answer:
C
Step-by-step explanation:
D: {-3,0,1,3}
R: {-5,-4,1,5}
PLZZZ HELP ITS FOR MY FINAL if 7a/8=14 then 12a=
Answers
So 12A would be (12*16)
So 12A= 192
complete the table y=x
Answers
The complete table of values of the linear equation is
x | y
0 | 0
1 | 1
2 | 2
3 | 3
How to make a table of values for the following equation?The linear equation of the function is given as
y = x
To complete the table, we assume values for x and then calculate the y values
So, we use the following values
x = 0, 1, 2, 3
Next, we substitute x = 0, 1, 2, 3 in the equation y = x
So, we have:
When x = 0
y = 0
When x = 1
y = 1
When x = 2
y = 2
When x = 3
y = 3
So, the complete table of values is
x | y
0 | 0
1 | 1
2 | 2
3 | 3
When represented as ordered pairs, we have
(x, y) = (0, 0), (1, 1), (2, 2) and (3, 3)
Read more about linear equation at
brainly.com/question/4074386
#SPJ1
A quality control engineer Is interested in the mean length of sheet insulation being cut automatically by machine. It is known that the standard deviation in the cutting length that this machine produces is 0.15 feet. A sample of 70 cut sheets yields a mean length of 12.14 feet. This sample will be used to obtain a confidence interval for the mean length cut by machine. Referring to problem statement, the Z value to use in obtaining the 99% confidence interval is approximately .A.1.645B. 1.96C.3.23D.2.58
Answers
Answer:
D.2.58
Step-by-step explanation:
We have that to find our \(\alpha\) level, that is the subtraction of 1 by the confidence interval divided by 2. So:
\(\alpha = \frac{1 - 0.99}{2} = 0.005\)
Now, we have to find z in the Ztable as such z has a pvalue of \(1 - \alpha\).
That is z with a pvalue of \(1 - 0.005 = 0.995\), so Z = 2.58.
The answer is given by option D.
simplify 8x+7-x-4
help meeeeee!!!
Answers
Answer:
7x + 3
Step-by-step explanation:
Let's simplify step-by-step.
8x + 7 − x − 4
= 8x + 7 + −x + −4
Combine Like Terms:
= 8x + 7 + −x + −4
= (8x + −x) + (7 + −4)
= 7x + 3
Answer:
= 7x + 3
hope this helps and is right. p.s i really need brainliest :)
if my answer is wrong then I am incredibly sorry!
Find a polynomial f(x) of degree 3 with real coefficients and the following zeros.-1,3-i
Answers
So the polynomial f(x) of degree 3 is
\(f(x)=x^3-5x^2+4x+10\)Find the slope of the line graphed

Answers
Check the picture below.

Use the given conditions to write an equation for the line in the indicated form.
Passing through (2, 2) and perpendicular to the line whose equation is y = 4x + 7;
point-slope form
A)y=-4x-10
B)y-2=-1/4(x-2)
C)y-2=1/4(x+2)
D)y-2=1/4(x-2)
Answers
Answer:
B) y - 2 = (-1/4)(x - 2)
Step-by-step explanation:
Start with the equation of the given line: y = 4x + 7.
Determine the slope of the given line, which is 4.
Since the perpendicular line has a negative reciprocal slope, the perpendicular line's slope is -1/4.
Use the point-slope form of a linear equation: y - y₁ = m(x - x₁), where (x₁, y₁) is the given point and m is the slope.
Substitute the values x₁ = 2 and y₁ = 2 into the point-slope equation: y - 2 = (-1/4)(x - 2).
Simplify by distributing -1/4 to (x - 2): y - 2 = (-1/4)x + 1/2.
Add 2 to both sides to isolate y: y = (-1/4)x + 1/2 + 2.
Simplify further: y = (-1/4)x + 5/2.
The equation in point-slope form for the line passing through (2, 2) and perpendicular to y = 4x + 7 is y - 2 = (-1/4)(x - 2), which matches option B.
If the function y=sin(x) is transformed to y = sin(2x), how does the graph change?
It is stretched vertically.
It is compressed vertically.
It is stretched horizontally.
It is compressed horizontally..
Answers
Step-by-step explanation:
The transformation y = sin(2x) affects the graph of y = sin(x) by compressing it horizontally.
The function y = sin(2x) has a coefficient of 2 in front of the x variable. This means that for every x value in the original function, the transformed function will have half the x value.
To see the effect of this transformation, let's compare the graphs of y = sin(x) and y = sin(2x) by plotting some points:
For y = sin(x):
x = 0, y = 0
x = π/2, y = 1
x = π, y = 0
x = 3π/2, y = -1
x = 2π, y = 0
For y = sin(2x):
x = 0, y = 0
x = π/2, y = 0
x = π, y = 0
x = 3π/2, y = 0
x = 2π, y = 0
As you can see, the y-values of the transformed function remain the same as the original function at every x-value, while the x-values of the transformed function are compressed by a factor of 2. This means that the graph of y = sin(2x) appears narrower or more "squeezed" horizontally compared to y = sin(x).
Therefore, the correct statement is: It is compressed horizontally.
What property is used to rewrite (x + 2)(y + z) as y (x + 2) + z (x + 2)
Answers
Answer:
Distributive Property
Step-by-step explanation (if you were to show the steps):
(x+2)(y+z) (first expression)
xy + xz + 2y + 2z (Distributive Property of Multiplication)
yx + 2y + zx + 2z (use the Commutative Property of Addition and Commutative Property of Multiplication to group xy (also known as yx) and 2y together, and to group xz (also known as zx) and 2z together)
y(x + 2) + z(x + 2) (use factoring to get the rewritten expression at the end)
2x - y = 8
x - 4y = -3
Answers
Answer:
X = 5
Y = 2
Step-by-step explanation:
y=2x-8
x-4(2x-8)=-3 -> x-8x+32=-3 -> -7x = -35 -> x=-35/-7 = 5
x=5 -> y=2x-8 -> y=2(5)-8=2
Answer:
x=5 y=2
Step-by-step explanation:
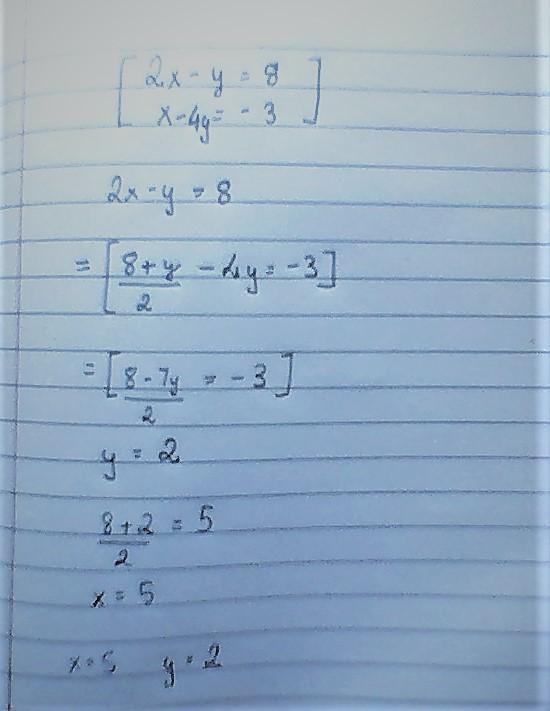
Choose the correct statement of the rule; then complete the table for missing values. A merchant adds $3.00 to his cost to determine his selling price.
The rule is:
c 1 2 3 4 5
f(c)
Answers
Answer:
Selling Price = Cost + $3.00
c 1, 2, 3, 4, 5,
f(c) 4, 5, 6, 7, 8,
The merchant uses Selling Price = Cost + $3.00 to determine the selling price.
What is Addition?Addition is a process of combining two or more numbers.
A merchant adds $3.00 to his cost to determine his selling price.
The cost is denoted by c.
The selling price is given by f(c).
As there is given add in the sentence, it means we have to use the addition rule.
Selling price is the sum of cost plus three
Selling Price = Cost + $3.00
So the table becomes as below
c 1, 2, 3, 4, 5,
f(c) 4, 5, 6, 7, 8,
Hence, the merchant uses Selling Price = Cost + $3.00 to determine the selling price.
To learn more on Addition click:
https://brainly.com/question/29053821
#SPJ2
Ben is decorating his home with vases of flowers. He bought glass vases that cost $22 each and ceramic vases that cost $14 each. The total cost of the vases came to more than $172. Also, Ben bought no more than 10 vases in all.
Which system of inequalities can be used to determine the number of glass vases, x, and the number of ceramic vases, y, that Ben could have bought?
Answers
The system of inequalities that can be used to determine the amounts is given by:
22x + 14y > 172.x + y < 11.What is a system of equations?A system of equations is when two or more variables are related, and equations are built to find the values of each variable.
A system of inequalities works similarly to a system of equations, just the equality symbol is replaced by an inequality symbol(less, more, different,...).
In this problem, the variables are:
Variable x: Number of glass vases.Variable y: Number of ceramic vases.He bought glass vases that cost $22 each and ceramic vases that cost $14 each. The total cost of the vases came to more than $172, hence:
22x + 14y > 172.
Also, Ben bought no more than 10 vases in all, hence:
x + y < 11.More can be learned about a system of equations at https://brainly.com/question/24342899
#SPJ1
Find the average value of the negative-valued function y=f(x), given that the area of the region bounded by the curve f(x) and x-axis from x=4 to x=10 is 13/5
Answers
Given that the area of the region bounded by the curve f(x) and x-axis from x=4 to x=10 is 13/5, the average value of the negative-valued function y=f(x) over the interval [4,10] is -13/30.
The average value of a function f(x) over an interval [a,b] is given by:
average value = (1/(b-a)) * integral from a to b of f(x) dx
In this case, we are given that the function y=f(x) is negative-valued, and the area of the region bounded by the curve and x-axis from x=4 to x=10 is 13/5. This means that the integral of f(x) over the interval [4,10] is equal to -13/5:
\(\int\limits^{10}_4 \, f(x) dx\) = -13/5
To find the average value of f(x) over this interval, we divide this integral by the length of the interval:
average value = (1/(10-4)) * \(\int\limits^{10}_4 \, f(x) dx\)
= (1/6) * (-13/5)
= -13/30
Therefore, the average value of the negative-valued function y=f(x) over the interval [4,10] is -13/30. This means that if we were to draw a horizontal line at the height of -13/30 over the interval [4,10], the area between this line and the x-axis would be equal to the area of the region bounded by the curve f(x) and x-axis over the same interval.
To learn more about curves click on,
https://brainly.com/question/14407388
#SPJ4
Kemani Walker
Law of Sines
Jun 15, 9:29:00 PM
?
In ATUV, t = 820 inches, m/U=132° and m2V=25°. Find the length of u, to the
nearest inch.
Answer: u =
Submit Answer
Answers
The length of u, to the nearest inch, is 1818 inches.
To solve this problem, we can use the Law of Sines, which states that the ratio of the length of a side of a triangle to the sine of its opposite angle is constant.
In this case, we'll use the following formula:
a/sin(A) = b/sin(B) = c/sin(C)
Let's label the sides and angles of the triangle:
Side a = u (length of u)
Side b = t (820 inches)
Side c = v (length of v)
Angle A = m/U (132°)
Angle B = m2V (25°)
Angle C = 180° - A - B (as the sum of angles in a triangle is 180°)
Now, we can use the Law of Sines to set up the equation:
u/sin(A) = t/sin(B)
Plugging in the given values:
u/sin(132°) = 820/sin(25°)
To find the length of u, we'll solve this equation for u.
u = (820 \(\times\) sin(132°)) / sin(25°)
Using a calculator, we can evaluate the right side of the equation to get the approximate value of u:
u ≈ (820 \(\times\) 0.9397) / 0.4226
u ≈ 1817.54 inches
Rounding to the nearest inch, we have:
u ≈ 1818 inches
For similar question on Law of Sines.
https://brainly.com/question/30401249
#SPJ8
There are 3 triangles and 15 circles. What is the simplest ratio of triangles to circles?
Answers
Answer:
1/5, 1:5, 1 to 5
Step-by-step explanation:
The ratio is 3/15, but simplest form is 1/5.
3(7-9k)+23k=4x-(24-k)
Answers

The image of point Q after a dilation of 4, and then a translation 2 units down is (8, 22). What was the y-coordinate of the original location of point Q?
Answers
Answer: 9 g
Step-by-step explanation:
3. If a 35-foot cable were run from the top of the pole and anchored to the ground at a distance from the pole, about how far away from the pole would it be anchored?
Answers
The distance from the pole at which the cable is anchored is about 25 feet from the pole .
Given that a 35-foot cable is run from the top of the pole and anchored to the ground at a distance from the pole. The problem is to determine about how far away from the pole would it be anchored.
Let AB be the pole of length 40 feet, and CD be the 35-foot long cable anchored to the ground at D and attached to the top of the pole at C. Let E be the point on the ground at which the cable is taut and is anchored. The distance ED is to be determined.
we can see that ∆CDE is a right-angled triangle with ∠CED = 90°.
Using Pythagoras Theorem, we have:CD² = CE² + DE²35² = (40 - ED)² + DE² .
Simplifying the above equation
1225 = 1600 - 80ED + ED²
1225 - 1600 + 80ED - ED² = 0ED² - 80ED + 375 = 0
Factorizing the above quadratic equation
ED² - 25ED - 15ED + 375 = 0ED(ED - 25) - 15(ED - 25)
= 0(ED - 15)(ED - 25) = 0So, ED = 15 ft or ED = 25 ft.
The negative value of ED is extraneous since it represents a point below the ground, which is not possible. Therefore, the distance from the pole at which the cable is anchored is about 25 feet from the pole.
Know more about distance here:
https://brainly.com/question/30395212
#SPJ8
