What is the solution to -2(8x-4) < 2x + 5?
x > 2/1/20
x < 1/1/20
x>6
x<6
Answers
The solution to the given Inequality i.e. -2(8x-4) < 2x + 5 is x>\(\frac{1}{6}\)
Inequality:
Inequality, A declaration of an order relationship between two numbers or algebraic expressions, such as greater than, greater than or equal to, less than, or less than or equal to. Equations can be used to address Inequality problems when they are stated as questions or as declarations of fact in the form of theorems.
Given that a Inequality i.e. -2(8x-4) < 2x + 5 and asked to find the solution of the given Inequality.
⇒ -2(8x-4) < 2x + 5
⇒ -16x+8 < 2x+5
⇒3< 18x
⇒x>\(\frac{1}{6}\)
Therefore,The solution to the given inequality i.e. -2(8x-4) < 2x + 5 is x>\(\frac{1}{6}\)
Learn more about Inequality here:
https://brainly.com/question/20383699
#SPJ4
Related Questions
In the following diagram,
What is the measure of
∠x

Answers
Answer:
Step-by-step explanation:
BAD = 42
x + 103 + 42 = 180
x = 180 - 145
x = 35
Expand the function.
f(x) = (3x-4)4
81x4 − 432x³ + [? ]x²
+
-
X +
PLS HELP
Answers
The expansion of the function \((3x - 4)^4\) simplifies to \(81x^4 - 432x^3 + 864x^2 - 768x + 256.\)
To expand the function \(f(x) = (3x - 4)^4\), we can use the binomial theorem. According to the binomial theorem, for any real numbers a and b and a positive integer n, the expansion of \((a + b)^n\) can be written as:
\((a + b)^n = C(n, 0)a^n b^0 + C(n, 1)a^{(n-1)} b^1 + C(n, 2)a^{(n-2)} b^2 + ... + C(n, n-1)a^1 b^{(n-1)} + C(n, n)a^0 b^n\)
where C(n, k) represents the binomial coefficient, which is given by C(n, k) = n! / (k!(n-k)!).
Applying this formula to our function \(f(x) = (3x - 4)^4\), we have:
\(f(x) = C(4, 0)(3x)^4 (-4)^0 + C(4, 1)(3x)^3 (-4)^1 + C(4, 2)(3x)^2 (-4)^2 + C(4, 3)(3x)^1 (-4)^3 + C(4, 4)(3x)^0 (-4)^4\)
Simplifying each term, we get:
\(f(x) = 81x^4 + (-432x^3) + 864x^2 + (-768x) + 256\)
Therefore, the expanded form of the function \(f(x) = (3x - 4)^4\) is \(81x^4 - 432x^3 + 864x^2 - 768x + 256\).
Note that the coefficient of \(x^3\) is -432, the coefficient of \(x^2\) is 864, the coefficient of x is -768, and the constant term is 256.
For more question on function visit:
https://brainly.com/question/11624077
#SPJ8
Note the complete question is
![Expand the function.f(x) = (3x-4)481x4 432x + [? ]x+-X + PLS HELP](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/GfWbZg9TGTD1FI7gZnK9lbVdLBpjkw5X.jpeg)
3 A farmer's horses drink from a rectangular water tank with dimensions shown.
2 4/5 ft
2 2/5 * ft
2 1/2 * 1
5 3/5 * ft
4 4/5 ft
When the farmer refills the tank, it takes the horses 4 days to drink all the water. The farmer wants to build a new, larger tank and plans to increase each measurement of the tank by 25%.
Section 3
By what percentage will the amount of water the farmer can put in the tank increase when the larger tank is built?
Explain how you found your answers.
Enter your answers and your explanation in the space provided.
How many days will it take the horses to drink all the water in the larger tank?

Answers
The amount of water the farmer can put in the tank increase when the larger tank is built is 106.33%.It takes 4days for the horses to drink all the water in the larger tank.
What is percentage?Percentage is a way of expressing a proportion or a fraction out of 100. It represents the number of parts per hundred of a quantity.
What does dimension refers to?Dimension refers to a measurable aspect of an object or a system, such as length, width, height, depth, volume, area, or mass. In mathematics, dimension also refers to the number of coordinates required to specify a point in a space. For example, a two-dimensional shape like a square has two dimensions, length and width, while a three-dimensional object like a cube has three dimensions, length, width, and height.
To find the percentage increase in the amount of water the farmer can put in the larger tank, we need to calculate the volume of the original tank and the volume of the larger tank, and then compare the two.
The original tank has dimensions of 2 4/5 ft, 2 2/5 ft, and 2 1/2 ft. We can convert these mixed numbers to improper fractions for easier calculations:
2 4/5 ft = (2 x 5 + 4)/5 ft = 14/5 ft
2 2/5 ft = (2 x 5 + 2)/5 ft = 12/5 ft
2 1/2 ft = (2 x 2 + 1)/2 ft = 5/2 ft
The volume of the original tank is then:
Volume = Length x Width x Height = 14/5 ft x 12/5 ft x 5/2 ft
Now, the farmer plans to increase measurement by 25%. To do this, we multiply each measurement by 1.25.
The dimensions of the larger tank would be:
Length = 14/5 ft x 1.25 = 3.5 ft
Width = 12/5 ft x 1.25 = 3 ft
Height = 5/2 ft x 1.25 = 3.125 ft
The volume of the larger tank is then:
Volume = Length x Width x Height = 3.5 ft x 3 ft x 3.125 ft
To find the percentage increase, we can compare the two volumes:
Percentage increase = ((Volume of larger tank - Volume of original tank) / Volume of original tank) x 100
Plugging in the values we found:
Percentage increase = ((3.5 ft x 3 ft x 3.125 ft - 14/5 ft x 12/5 ft x 5/2 ft) / (14/5 ft x 12/5 ft x 5/2 ft)) x 100
After calculating the above expression, we find that the percentage increase is approximately 106.33%. So, the amount of water the farmer can put in the larger tank will increase by approximately 106.33% when the larger tank is built.
Now, to find how many days it will take the horses to drink all the water in the larger tank, we can assume that the rate at which the horses drink water remains constant. Since the volume of the larger tank is approximately 106.33% more than the original tank, it will take the horses approximately the same amount of time to drink all the water in the larger tank, which is 4 days.
Learn more about rectangle here:
https://brainly.com/question/29123947
#SPJ1
1AcellusFind the area of the shaded region.Help Resources80°5 cmA = [?] cm2Enter a decimal rounded to the nearest tenth.Enter
Answers
The formula for finding the area of the unshaded segment is given as
\(A=(\frac{\pi\theta}{360}-\frac{\sin \theta}{2})r^2\)Given the following parameters,
π = 3.14
θ = 80°
r = 5 cm
Substituting,
\(\begin{gathered} A=(\frac{3.14\times80}{360}-\frac{\sin \text{ 80}}{2})\times5^2 \\ =(\frac{251.2}{360}-\frac{0.9848}{2})\times25 \\ =(0.6978-0.4924)\times25 \\ =0.2054\times25 \\ =5.135\approx5.1\operatorname{cm}^2 \end{gathered}\)To find the area of the shaded portion, we would subtract the area of the unshaded segment from the area of the circle.
Area of circle = πr²
\(3.14\times5^2=78.5\operatorname{cm}^2\)Therefore,
The area of the shaded region = 78.5 - 5.1 = 73.4 cm²
determine whether a triangle with these side lengths would be acute, right, or obtuse: 5, 7, and 10;
Answers
Answer:
obtuse
Step-by-step explanation:
Let 5 = a, 7 = b, 10 = c
if a^2 + b^2 = c^2, then the triangle is a right triangle by the converse of the Pythagorean Theorem
If a^2 + b^2 > c^2, then the triangle is an acute triangle by Theorem 8-4
if a^2 + b^2 < c^2, then the triangle is an obtuse triangle by Theorem 8-3
a^2 = 25
b^2 = 49
c^2 = 100
25 + 49 < 100, therefore the triangle is an obtuse
prove that tan theta * sin theta = (1 - cos^2 theta)/(sqrt(1 - sin^2 theta))
Answers
Answer:
This identity holds as long as \(\displaystyle \theta \ne k\, \pi + \frac{\pi}{2}\) for all integer \(k\).
For the proof, make use of the fact that:
\(\displaystyle \tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)}\) (definition of tangents,) and
\(\cos(\theta) = \sqrt{1 - \sin^{2}(\theta)}\) (Pythagorean identity,) which is equivalent to \(1 - \cos^{2}(\theta) = \sin^{2}(\theta)\).
Step-by-step explanation:
Assume that \(\displaystyle \theta \ne k\, \pi + \frac{\pi}{2}\) for all integer \(k\). This requirement ensures that the \(\tan(\theta)\) on the left-hand side takes a finite value. Doing so also ensures that the denominator \(\sqrt{1 - \sin^2(\theta)}\) on the right-hand side is non-zero.
Make use of the fact that \(\displaystyle \tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)}\) to rewrite the left-hand side:
\(\begin{aligned} & \tan(\theta) \cdot \sin(\theta) \\ =&\; \frac{\sin({\theta})}{\cos({\theta})} \cdot \sin(\theta) \\ =&\; \frac{\sin^{2}(\theta)}{\cos(\theta)}\end{aligned}\).
Apply the Pythagorean identity \(\sin^{2}(\theta) = 1 - \cos^{2}(\theta)\) and \(\cos(\theta) = \sqrt{1 - \sin^{2}(\theta)}\) to rewrite this fraction:
\(\begin{aligned} & \frac{\sin^{2}(\theta)}{\cos(\theta)}\\ =\; &\frac{1 - \cos^{2}(\theta)}{\cos(\theta)}\\ =\; & \frac{1 - \cos^{2}(\theta)}{\sqrt{1 - \sin^{2}(\theta)}}\end{aligned}\).
Hence, \(\displaystyle \tan(\theta) \cdot \sin(\theta) = \frac{1 - \cos^{2}(\theta)}{\sqrt{1 - \sin^{2}(\theta)}}\).
A local hamburger shop sold a combined total of 392 hamburgers and cheeseburgers on Thursday. There were 58 fewer cheeseburgers sold than hamburgers.
How many hamburgers were sold on Thursday?
Answers
Answer:
Step-by-step explanation:
x = hamburgers
x - 58 = cheeseburgers
392 = total of both sold
x + (x - 58) = 392
x + x - 58 + 58 = 392 + 58
x + x = 450
2x = 450
Divide both sides by 2
2x/2 = 450/2
x = 225
The number of hamburgers sold was 225
Consider a medium with parameters € = 1.2 (10^-10 )F/m , n= 3(10^-3) H/m and sigma=0. Magnetic field intensity in the medium is given as R = 2cos (10^10t- 600x)äz Am.
Use Maxwell's equations to obtain the followings:
1) Magnetic flux density
These questions is circuit theory
Answers
Using Maxwell's equations, we can determine the magnetic flux density. One of the Maxwell's equations is:
\(\displaystyle \nabla \times \mathbf{H} = \mathbf{J} + \frac{\partial \mathbf{D}}{\partial t}\),
where \(\displaystyle \nabla \times \mathbf{H}\) is the curl of the magnetic field intensity \(\displaystyle \mathbf{H}\), \(\displaystyle \mathbf{J}\) is the current density, and \(\displaystyle \frac{\partial \mathbf{D}}{\partial t}\) is the time derivative of the electric displacement \(\displaystyle \mathbf{D}\).
In this problem, there is no current density (\(\displaystyle \mathbf{J} =0\)) and no time-varying electric displacement (\(\displaystyle \frac{\partial \mathbf{D}}{\partial t} =0\)). Therefore, the equation simplifies to:
\(\displaystyle \nabla \times \mathbf{H} =0\).
Taking the curl of the given magnetic field intensity \(\displaystyle \mathbf{R} =2\cos( 10^{10} t-600x)\hat{a}_{z}\, \text{Am}\):
\(\displaystyle \nabla \times \mathbf{R} =\nabla \times ( 2\cos( 10^{10} t-600x)\hat{a}_{z}) \, \text{Am}\).
Using the curl identity and applying the chain rule, we can expand the expression:
\(\displaystyle \nabla \times \mathbf{R} =\left( \frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial y} -\frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial z}\right) \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Since the magnetic field intensity \(\displaystyle \mathbf{R}\) is not dependent on \(\displaystyle y\) or \(\displaystyle z\), the partial derivatives with respect to \(\displaystyle y\) and \(\displaystyle z\) are zero. Therefore, the expression further simplifies to:
\(\displaystyle \nabla \times \mathbf{R} =-\frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial x} \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Differentiating the cosine function with respect to \(\displaystyle x\):
\(\displaystyle \nabla \times \mathbf{R} =-2( 10^{10}) \sin( 10^{10} t-600x)\hat{a}_{z} \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Setting this expression equal to zero according to \(\displaystyle \nabla \times \mathbf{H} =0\):
\(\displaystyle -2( 10^{10}) \sin( 10^{10} t-600x)\hat{a}_{z} \mathrm{d} x\mathrm{d} y\mathrm{d} z =0\).
Since the equation should hold for any arbitrary values of \(\displaystyle \mathrm{d} x\), \(\displaystyle \mathrm{d} y\), and \(\displaystyle \mathrm{d} z\), we can equate the coefficient of each term to zero:
\(\displaystyle -2( 10^{10}) \sin( 10^{10} t-600x) =0\).
Simplifying the equation:
\(\displaystyle \sin( 10^{10} t-600x) =0\).
The sine function is equal to zero at certain values of \(\displaystyle ( 10^{10} t-600x) \):
\(\displaystyle 10^{10} t-600x =n\pi\),
where \(\displaystyle n\) is an integer. Rearranging the equation:
\(\displaystyle x =\frac{ 10^{10} t-n\pi }{600}\).
The equation provides a relationship between \(\displaystyle x\) and \(\displaystyle t\), indicating that the magnetic field intensity is constant along lines of constant \(\displaystyle x\) and \(\displaystyle t\). Therefore, the magnetic field intensity is uniform in the given medium.
Since the magnetic flux density \(\displaystyle B\) is related to the magnetic field intensity \(\displaystyle H\) through the equation \(\displaystyle B =\mu H\), where \(\displaystyle \mu\) is the permeability of the medium, we can conclude that the magnetic flux density is also uniform in the medium.
Thus, the correct expression for the magnetic flux density in the given medium is:
\(\displaystyle B =6\cos( 10^{10} t-600x)\hat{a}_{z}\).
Find the surface area of the solid below. Round to the nearest tenth if needed.
Can someone help plsss

Answers
HELPPP PLEASE YOU DONT NEED NO WORK SHOWN!!

Answers
Answer:
140.22
Step-by-step explanation:
What is the loca extrema/ absolute of the polynomial 10x^5 + 22x^4 + 20x^3 -0x^2 + 6

Answers
(a) The local extrema of the polynomial are: Local maximum at x = -0.68 and Local minimum at x = -0.32
(b) There is no global minimum or maximum.
What are the local extrema of the polynomial?To find the local extrema and absolute extrema of the given polynomial 10x⁵ + 22x⁴ + 20x³ - 0x² + 6, we need to take the first and second derivatives of the polynomial and find the critical points.
The first derivative is:
50x⁴ + 88x³ + 60x²
The second derivative is:
200x³ + 264x² + 120x
Setting the first derivative to zero, we get:
50x⁴ + 88x³ + 60x² = 0
Factoring out x², we get:
x²(50x² + 88x + 60) = 0
Using the quadratic formula to solve for the roots of the quadratic equation 50x² + 88x + 60 = 0, we get:
x = -0.68 or x = -0.32
These are the critical points of the polynomial. To determine whether they correspond to local extrema or inflection points, we need to look at the sign of the second derivative at each point.
Substituting x = -0.68 into the second derivative, we get:
200(-0.68)³ + 264(-0.68)² + 120(-0.68) = -148.68
Since the second derivative is negative at x = -0.68, this critical point corresponds to a local maximum.
Substituting x = -0.32 into the second derivative, we get:
200(-0.32)³ + 264(-0.32)² + 120(-0.32) = 9.48
Since the second derivative is positive at x = -0.32, this critical point corresponds to a local minimum.
To find the absolute extrema, we also need to evaluate the polynomial at the endpoints of the interval we are interested in. Since the polynomial does not have any real roots, we can assume that the interval of interest is the entire real line.
Taking the limit of the polynomial as x approaches positive or negative infinity, we see that the leading term dominates and the polynomial goes to positive infinity as x approaches infinity and negative infinity.
Therefore, there is no global minimum or maximum.
Learn more about local extrema here: https://brainly.com/question/29278261
#SPJ1
Video Wa community into four adve graph shows the total number of each zone for a three-week period. 1,000 900 800 700 600 500 400 300 200 100 0 Number of Customers Zone 1 Video Warehouse Zone 2 Zone 3 A. 3:5 OB. 3:2 OC. 2:1 OD. 1:2 Zone 4 1. During the three weeks, how many customers came from Zones 3 and 4? A. between 900 and 1,000 B. between 1,000 and 1,100 C. between 1,100 and 1,200 D. between 1,200 and 1,300 2. Approximately what is the ratio of custo from Zone 1 to customers from Zone 3
Answers
The total number of each zone for a three-week period is between 1200 and 1300, 1:2 is the ratio of customer from Zone 1 to customers from Zone 3.
1) During 3 weeks bound
Customers from zone 3 = 900
Customers from zone 4 = 320
So, total customers = (900 + 320)
= 1220
Hence, option D is correct i.e between 1200 and 1300.
2) Customer from zone 1 = 450
Customers from zone 3 = 900
So, Customer from zone 1 / Customer from zone 3 = 450/900
= 1/2
Hence, option 2 i.e., 1:2 is correct.
3) 3/5 pound of clay is used to make = 1 bowl
So, 1 bound of clay is used to make = 5/3 bowl
By unitary method,
10 pounds of clay is used to make = 10 *(5/3)
= 16.66
= 17 bowls (approx)
Hence, option d is correct answer.
Therefore, The total number of each zone for a three-week period is between 1200 and 1300, 1:2 is the ratio of customer from Zone 1 to customers from Zone 3.
To know more about pounds check the below link:
https://brainly.com/question/28571689
#SPJ9
what is the value of h

Answers
Answer:
h = 5.318 m
Step-by-step explanation:
6.5/11 = h/9
0.5909 = h/9
h = 5.318
Answer:
Height: 5.32
Step-by-step explanation:
Area=29.24
Heron's Formula
You deposit $5000 in an account earning 5% interest compounded continuously. How much will you have in the account in 5 years? Round to the nearest cent.
Answers
Given the table below, what is the x-intercept of the linear function?

Answers
Answer:
-6
Step-by-step explanation:
please help me with my online classwork!

Answers
Answer:
840 cm²---------------------------
There are two triangular faces with base of 16 cm and height of 15 cm and three rectangular faces.
Find the sum of areas of all five faces:
S = 2*(1/2)*16*15 + (17*2 + 16)*12 = 240 + 600 = 840I’m stuck again on this one

Answers
Answer:
8.7 cm
Step-by-step explanation:
Since all sides of the given shape are equal, so it is a cube.
So length of the diagonal of cube is give as:
\(l(diagonal) = l \sqrt{3} \\ \\ = 5 \times 1.732 \\ \\ = 8.66 \\ \\ l(diagonal) \approx8.7 \: cm\)
Which similarity statement is true for rectangles JKLM and PQRS, given that JK=6, JM=5, QR=15, and PQ=12.5? A. rectangle JKLM ~ rectangle PQRS B. rectangle JKLM ~ rectangle QRSP C. rectangle JKLM ~ rectangle RQPS D.rectangle JKLM~ rectangle SRQP

Answers
Answer:
B: rectangle JKLM ~ rectangle QRSP
Step-by-step explanation:
5/6=0.83
12.5=0.83
JK corresponds to QR
JM corresponds to PQ
rectangle JKLM ~ rectangle QRSP
ƒ(t) = –1∕2t2 + 2t + 6
Answers
This function represents a downward-opening parabola with a vertical shift of 6 units upward.
How to explain the functionThe given function is Ƒ(t) = –1/(2t²) + 2t + 6.
This is a quadratic function in terms of t. The general form of a quadratic function is f(t) = at² + bt + c, where a, b, and c are constants.
Comparing the given function Ƒ(t) = –1/(2t²) + 2t + 6 with the general form, we can see that a = -1/2, b = 2, and c = 6.
So, the function Ƒ(t) can be written as:
Ƒ(t) = (-1/2)t² + 2t + 6
This function represents a downward-opening parabola with a vertical shift of 6 units upward.
Learn more about functions on
https://brainly.com/question/11624077
#SPJ1
A bank's loan officer rates applicants for credit. the ratings are normally distributed with a mean of 200 and a standard deviation of 50. if an applicant is randomly selected, find the probability of a rating that is between 200 and 275.
Answers
Answer:
0.4332 = 43.32% probability of a rating that is between 200 and 275.
Step-by-step explanation:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
A bank's loan officer rates applicants for credit. the ratings are normally distributed with a mean of 200 and a standard deviation of 50
This means that \(\mu = 200, \sigma = 50\).
Find the probability of a rating that is between 200 and 275.
This is the pvalue of Z when X = 275 subtracted by the pvalue of Z when X = 200. So
X = 275
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{275 - 200}{50}\)
\(Z = 1.5\)
\(Z = 1.5\) has a pvalue of 0.9332
X = 200
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{200 - 200}{50}\)
\(Z = 0\)
\(Z = 0\) has a pvalue of 0.5
0.9332 - 0.5 = 0.4332
0.4332 = 43.32% probability of a rating that is between 200 and 275.
Mandy spent $75 and then earned $75.
Answers
Answer:
So that's 75$ back.....
please help i don’t feel like typing

Answers
Answer: q=13
Step-by-step explanation:
add the separate the q, add 4 to the 9= 13
13=q
Which situation can be represented by this inequality? 135 ≤ 10r + 15 Question 8 options: Hugo has 10 songs in his music player. He will add 15 songs every month. Hugo collects songs for r months. For what values of r will Hugo have at most 135 songs? Hugo has 10 songs in his music player. He will add 15 songs every month. Hugo collects songs for r months. For what values of r will Hugo have at least 135 songs? Hugo has 15 songs in his music player. He will add 10 songs every month. Hugo collects songs for r months. For what values of r will Hugo have at most 135 songs? Hugo has 15 songs in his music player. He will add 10 songs every month. Hugo collects songs for r months. For what values of r will Hugo have at least 135 songs?
Answers
Answer:
Hugo has 10 songs in his music player. He will add 15 songs every month. Hugo collects songs for r months. For what values of r will Hugo have at most 135 songs?
Step-by-step explanation:
took test 100%
find all other zeros of p (x)= x^3-x^2+8x+10, given that 1+3i is a zero. ( if there is more than one zero, separate them with commas.)edit: if possible please double check answers would high appreciate it.
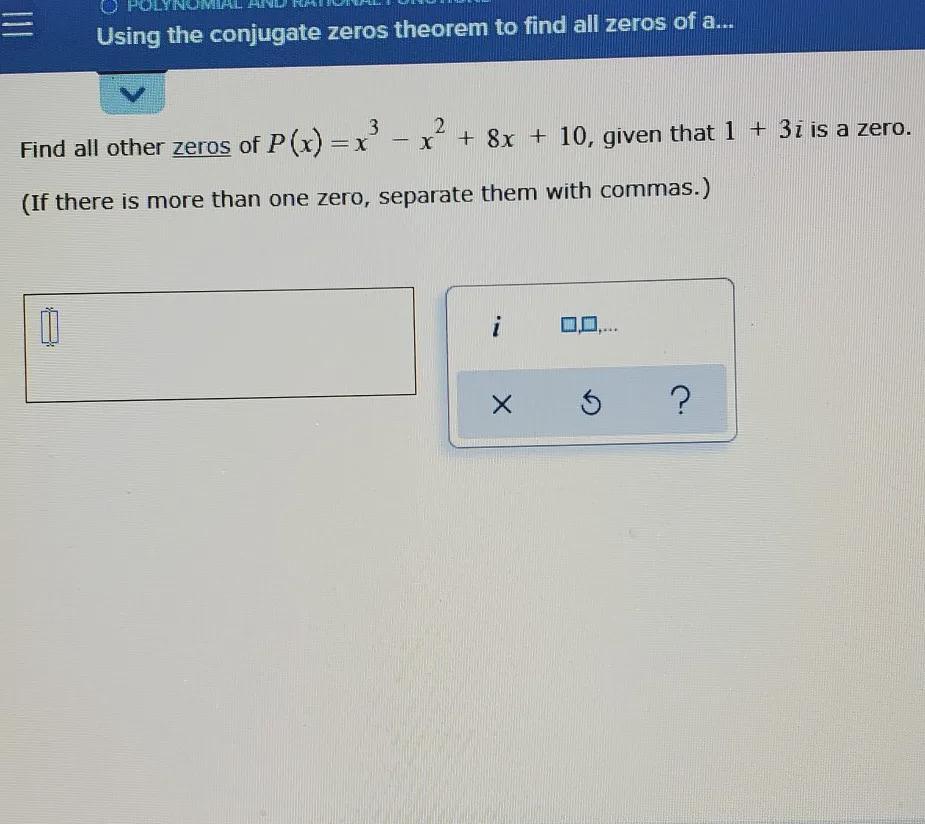
Answers
Since we have that 1 + 3i is one zero of p(x), then we have that its conjugate is also a root, then, we have the following complex roots for p(x):
\(\begin{gathered} x=1-3i \\ x=1+3i \end{gathered}\)also, notice that if we evaluate -1 on p(x), we get:
\(\begin{gathered} p(-1)=(-1)^3-(-1)^2+8(-1)+10=-1-1-8+10 \\ =-10+10=0 \end{gathered}\)therefore, the zeros of p(x) are:
x = 1-3i
x = 1+3i
x = -1
If you deposite €250 in a high earning account paying 9% compound interest and leave it 3 years.what will be the balance on the account at the end of that time
Answers
Answer:
ok, here is your answer
Step-by-step explanation:
Using the formula for compound interest:
A = P (1 + r/n)^(nt)
where:
A = the total amount
P = the principal amount
r = the annual interest rate (as a decimal)
n = the number of times the interest is compounded per year
t = the number of years
Given:
P = €250
r = 9% = 0.09
n = 1 (compounded annually)
t = 3 years
Now, substituting the given values in the formula:
A = 250 (1 + 0.09/1)^(1*3)
A = 250 (1 + 0.09)^3
A = 250 (1.09)^3
A = 250 (1.29503)
A = €323.76 (rounded to two decimal places)
Therefore, the balance in the account at the end of 3 years would be €323.76.
mark me as brainliestPick a point along the line and use the coordinates X on the web for blood into the Y equals MX plus be equation and solve for him, your rate of change! What are the number of passengers per hour?

Answers
5
1) Since this is a line of best fit, actually we are going to find an approximation for that.
2) Locating two points along the line, we've got (1,30) and (7,60) so let's find the rate of change:
\(m=\frac{y_2-y_1}{x_2-x_1}=\frac{60-30}{7-1}=\frac{30}{6}=5\)So, the rate of change relative to the scatter plot is 5
For any numbers a, b, and n, the expression (a.b)" is equal to abb.

Answers
Answer:
false because it only equal when b = n
Pipers Pizza shop used 18% more cheese this month than last month, due to having a discount on the extra chesse toppings. If the pizza shop used 150 pounds of cheese last month how much did it use this month
Answers
Answer:
177 pounds
Step-by-step explanation:
Create an equation to represent the system.
Since it's 18% more than what was used last month an equation can be written such as the one below:
(118%)( last month's cheese ) = this month's cheese
Convert the percentages into decimals by moving the decimal place at the end of 118.00 two places to the left
118% = 1.18
( 1.18 )( last month's cheese ) = this month's cheese
Next, plug in the number for last month's cheese
( 1.18 )( 150 pounds) =
177 pounds
for each parallel lines. you are given the measure of one angle
Answers
Answer:
The question is not complete
The second terms u_{2} and the sixth terms u_{6} of a geometric sequence (u_{n}) are 6 and -486. What is the first term u_{1} of this sequence?
Answers
The first term of the sequence is u₁ = 2.
In a geometric sequence, each term is found by multiplying the previous term by a constant ratio. Let's denote the first term as u₁ and the common ratio as r.
Given information:
u₂ = 6
u₆ = 486
We can use the formula for the nth term of a geometric sequence:
uₙ = u₁ x r^(n-1)
Plugging in the values for the second term (n = 2) and the sixth term (n = 6), we get:
u₂ = u₁ x r²⁻¹ = u₁ x r
u₆ = u₁ x r⁶⁻¹ = u₁ x r⁵
We can set up a system of equations with these two equations:
u₂ = 6 --> u₁r = 6 ...(1)
u₆ = 486 --> u₁ r⁵ = 486 ...(2)
Dividing equation (2) by equation (1), we get:
(u₁r⁵) / (u₁r) = (486) / 6
Simplifying the equation:
r⁴ = 81
Taking the fourth root of both sides:
r = √(81)
Therefore,
u₁ = 6/3
u₁ = 2.
To learn more about the geometric sequence;
https://brainly.com/question/11266123
#SPJ1