what is the standard error for the sample proportion if n=75 and p=0.3? round to 2 decimal places.
Answers
The standard error for the sample proportion when n=75 and p=0.3 is :
0.06 ( rounded to two decimal places )
To calculate the standard error for the sample proportion when n=75 and p=0.3, follow these steps:
1. Identify the sample size (n) and proportion (p): n=75, p=0.3
2. Calculate the complement of the proportion (1-p): q = 1 - p = 1 - 0.3 = 0.7
3. Use the formula for standard error of a proportion: SE = √(p * q / n)
4. Plug in the values: SE = √(0.3 * 0.7 / 75)
5. Calculate: SE ≈ 0.0563
The standard error for the sample proportion when n=75 and p=0.3 is approximately 0.06, rounded to two decimal places.
To learn more about standard error visit : https://brainly.com/question/1191244
#SPJ11
Related Questions
A recent study considered the effects of innovation on employment in Latin America. It seems reasonable that as more firms produce new products, they would need more workers, and employment would rise. For small firms in Argentina, let y be the yearly percentage of employment growth and let x be the percentage of small firms that are product or process innovators. Assume the estimated regression line is y=−5.399+5.790x. Suppose σ=1.5. Find the probability that an observed value of Y is more than 19 when x=4. Round your answer to four decimal places. P(Y>19)=
Answers
The probability that an observed value of Y is more than 19, given x=4 and the regression model y=−5.399+5.790x with σ=1.5, is approximately 0.2031.
What is the probability that the observed value of Y exceeds 19, considering x=4 and the given regression model?To find the probability that an observed value of (Y) is more than 19 when (x = 4) in the given regression model (Y = -5.399 + 5.790x), we need to calculate the z-score and then find the corresponding probability using the standard normal distribution.
First, we calculate the predicted value of (Y) when (x = 4) using the regression equation:
\(\[Y = -5.399 + 5.790 \times 4 = 17.761\]\)
Next, we calculate the z-score using the formula:
\(\[z = \frac{Y - \mu}{\sigma} = \frac{19 - 17.761}{1.5} \approx 0.8267\]\)
Now, we can find the probability (P(Y > 19)) by finding the area to the right of the z-score of 0.8267 in the standard normal distribution. Using a standard normal distribution table or calculator, we find the probability to be approximately 0.2031.
Therefore,\(\(P(Y > 19) = 0.2031\)\) (rounded to four decimal places).
The probability calculated assumes that the errors in the regression model follow a normal distribution with a standard deviation of \(\(\sigma = 1.5\)\).
Learn more about probability
brainly.com/question/31828911
#SPJ11
7.
(05.02)
A system of equations is shown below:
x + y = 3
2x − y = 6
The x-coordinate of the solution to this system of equations is
. (4 points)
Answers
Answer:
x = 3
Step-by-step explanation:
Given the 2 equations
x + y = 3 → (1)
2x - y = 6 → (2)
Adding the 2 equations term by term eliminates the y- term, that is
3x = 9 ( divide both sides by 3 )
x = 3
what fraction of 60 is the number 12?
Answers
Answer:
\(\frac{2}{5\\}\)
Step-by-step explanation:
Rlly Hope this helps! :)
Let's simplify the fraction 12/60.
=> 12 ÷ 12/60 ÷ 12=> 1/5Hence, the fraction is 1/5.
\(BrainiacUser1357\)
NEED HELP ASAP!!!!!!!!!!!!!!!!!!!!!!

Answers
The future value of $400 saved each year for 8 years at 7 percent. (Round your factor to 3 decimal places and ึ inal answer to 2 decimal places.) c. The amount a person would have to deposit today (present value) at a 10 percent interest rate to have $3,100 five years from now. (Round your factor to 3 decimal places and final answer to 2 decimal places.) d. The amount a person would have to deposit today to be able to take out $500 a year for 8 years from an account earning 7 percent. (Round your factor to 3 decimal places and final answer to 2 decimal places.)
Answers
For part c, the present value needed to have $3,100 five years from now at a 10 percent interest rate would be approximately $2,174.35.
For part d, the amount that needs to be deposited today to be able to withdraw $500 a year for 8 years from an account earning 7 percent would be approximately $2,992.71.
c. To calculate the present value needed to have $3,100 five years from now at a 10 percent interest rate, we can use the formula for present value of a future amount: PV = FV / (1 + r)^n, where PV is the present value, FV is the future value, r is the interest rate, and n is the number of years. Plugging in the values, we have PV = 3100 / (1 + 0.10)^5 ≈ $2,174.35.
d. To determine the amount that needs to be deposited today to be able to withdraw $500 a year for 8 years from an account earning 7 percent, we can use the formula for the present value of an annuity: PV = PMT × [(1 - (1 + r)^-n) / r], where PV is the present value, PMT is the annuity payment, r is the interest rate, and n is the number of periods. Plugging in the values, we have PV = 500 × [(1 - (1 + 0.07)^-8) / 0.07] ≈ $2,992.71.
Learn more about interest rate here:
https://brainly.com/question/27743950
#SPJ11
Solve the equation for exact solutions in the interval [0°,360°). Use an algebraic method. (cot 0-√3)(√2 sin 0+1)=0 Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The solution set is (Simplify your answers. Type an integer or a fraction. Use a comma to separate answers as needed. Do not include the degree symbol in your answer.) B. The solution is the empty set.
Answers
Answer:
30,135,210,225
Step-by-step explanation:
\(( \cot( \alpha ) - \sqrt{3} )( \sqrt{2} \sin( \alpha ) + 1) = 0\)
Set both equal to 0
\( \cot( \alpha ) = \sqrt{3} \)
\( \alpha = 30\)
Cot has a period of 180 degrees so the other value is
\( \alpha = 210\)
For the other factor,
\( \sqrt{2} \sin( \alpha ) + 1 = 0\)
\( \sin( \alpha ) = - \frac{1}{ \sqrt{2} } \)
Rationalize the denominator
\( \sin( \alpha ) = - \frac{ \sqrt{2} }{2} \)
\( \alpha = 135\)
Sin is reflective about the origin so if we find the distance from the original alpha , we get our other
\( \alpha = 225\)
answer.
So our solution set is
30,135,210,225
in the right angled triangle abc below ab =bc. the size of C is..

Answers
So we know B is 90 since it’s a right triangle
and A and C have to be the same
So 180-90=90
Then divide by 2
90/2=45
Answer:
45°
Step-by-step explanation:
AB and BC are congruent which mean ∠BAC and ∠BCA are congruent.
We already know ∠ABC is 90°.
We cans set up the equation with what is given.
180 = 90 + 2c
Subtract 90 from both sides.
90 = 2c
Divide both sides by 2
45 = C
So angle C is 45°
what is 0x3d (base 16) in decimal (base 10).
Answers
The hexadecimal number 0x3d is equal to 61 in decimal (base 10).
To convert the hexadecimal number 0x3D to decimal (base 10), we need to understand the positional system of both bases. In hexadecimal, each digit represents a power of 16, starting from the rightmost digit. The digits range from 0 to 9, and then from A to F, where A represents 10 and F represents 15, In hexadecimal (base 16) representation, each digit can have values from 0 to 15. The digits from 0 to 9 represent their respective values, and the letters A to F represent the values 10 to 15.
To convert 0x3d to decimal, we can break down the number as follows:
0x3d = (3 * 16^1) + (13 * 16^0)
Simplifying the expression:
0x3d = (3 * 16) + 13
0x3d = 48 + 13
0x3d = 61
learn more about hexadecimal here:
https://brainly.com/question/28875438
#SPJ11
Transform the equation to isolate x: ax = bx + 1. How is the value of x related to the difference of a and b?
(please help me)
Answers
Answer:
x = 1/a-b.
x is the reciprocal of the difference of a and b.
x is 1 over the difference of a and b.
x is the quotient of 1 and the difference of a and b.
Step-by-step explanation:
i did it
The transformation of the given equation ax = bx + 1 for the x will be 1/(a - b).
What is the substitution of an equation?In the by substitution method, one of the equations is calculated for one of the variables, which is then transferred back into the other equation where the chosen variable is a replacement, and the second equation is then calculated for. The first variable is then home safely.
In other words, substitution is a method to find the value of variables x and y by just substituting x and y to another equation.
The substitution method is more good than the elimination method.
Given that the equation
ax = bx + 1
Transfer bx to the left side
ax- bx = 1
Take common x from the left-hand side
x(a - b) = 1
Divide a - b on both sides
x = 1/(a - b) hence it will be the correct transformation.
For more about the substitution method
https://brainly.com/question/22340165
#SPJ2
49×7³×100. -----------------. 10³×3³×7²
Answers
Please mark me brainliest

I WILL NAME BRAINLYIST
A scientist uses a submarine to study ocean life.
• She begins 164 feet below sea level.
• After traveling down for 8 seconds, she's 233 feet below sea level.
Find the rate of change in the submarine's elevation in feet per second. Round your
answer to the nearest tenth.
Answers
Answer:
- 8.6 feet per second
Step-by-step explanation:
Step 1: - 233 feet (final) + 164 feet (start) = - 69
Step 2: - 69 divided by 8 seconds (time) = About - 8.6
The answer is negative because the submarine is below sea level.
write the equation for a parabola with a focus at (-8,-1) and a directrix at y= -4y =
Answers
Since the directrix is y=-4, use the equation of a parabola that opens up or down.
\(\mleft(x-h\mright)^2=4p(y-k)\)where vertex is at (h,k) and focus is at (h,k+p)
The vertex is halfway between the directrix and focus. Find the y-coordinate of the vertex using the following
\((-8,\frac{-1-4}{2})=(-8,-\frac{5}{2})\)Find the distance from the focus to the vertex.
The distance from the focus to the vertex and from the vertex to the directrix is |p|. Subtract the y-coordinate of the vertex from the y-coordinate of the focus to find p.
\(p=-1+\frac{5}{2}=-\frac{2}{2}+\frac{5}{2}=\frac{-2+5}{2}=\frac{3}{2}\)Substitute in the known values for the variables into the equation
\((x-h)^2=4p(y-k)\)\((x+8)^2=4\cdot\frac{3}{2}\cdot(y+\frac{5}{2})\)Simplify
\((x+8)^2=6\cdot(y+\frac{5}{2})\)in y=ax^2+bx+c form:
\(\begin{gathered} x^2+16x+64=6y+15 \\ x^2+16x+64-15=6y \\ x^2+16x+49=6y \\ y=\frac{1}{6}x^2+\frac{16}{6}x+\frac{49}{6} \end{gathered}\)I have looked from answer sheet but i still didn’t get it…

Answers
Answer:
Xyz E number
Step-by-step explanation:
I think Xyz is right
Answer:
A. AB = xyzx
Step-by-step explanation:
You want AB when A = BC, B = x, and C = yz.
SubstitutionYou can evaluate the unknown expression by making substitutions until you can't anymore.
AB = (BC)(B) . . . . . . . . substitute BC for A
AB = ((x)(yz))(x) . . . . . . substitute x for B (2 places), yz for C
AB = xyzx . . . . . . . . . . remove the unnecessary parentheses
Type the expressions as radicals.
q 3/2
Answers
√q³ your answer
pls mark me in branlist
Mr. Steiner purchased a car for about $14,000. Assuming his loan was
compounded monthly at an interest rate of 4. 9% for 72 months:
p=
r=
n=
t=
A. How much will he have paid total?
B. How much more did he pay than the price of the car?
Answers
Mr. Steiner will need to pay $18774 in total and he paid $4774 more than the actual price of the car.
we know that the amount of money earned, in compound interest after t years is showed as, A(t) = P (1+\(\frac{r}{n}\))ⁿ\(^{t}\)
here, we know that A(t) is the amount of money after t years.
P is the initial sum of money, know as principal,
r is the interest rate as a decimal value,
n is the number of times that interest is compounded per year,
and
t is the time in years for which the money is invested or borrowed.
now here we know,
P = 14000, r = 0.049, n = 12, t = 6
when we have all values we can find,
A(t) = P(1+\(\frac{r}{n}\))ⁿ\(^{t}\)
A(6) = 14000 (1+\(\frac{0.049}{12}\))¹²ˣ⁶
A(6) = 18774
therefore we know that Mr. Steiner needs to pay $18774 in total.
now,
18774 - 14000 = 4774
therefore we get to know that Mr. Steiner paid $4774 more than the actual price of the car.
To learn more about compound interest, click here:
brainly.com/question/13001287
#SPJ4
All of the following have the same solution except ___
•50=5m
•x-6=4
•w/5=2
•b+2=8

Answers
If u replace b as 10 it would be 10+2=12 which is not right so the answer would be b+2=8
The line passing through (-3 , -6) and (d, -5d) has a gradient of -3.
Find the value of d.
Answers
Answer:
d = 7.5
Step-by-step explanation:
Calculate the slope m using the slope formula and equate to - 3
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = (- 3, - 6) and (x₂, y₂ ) = (d, - 5d)
m = \(\frac{-5d+6}{d+3}\) = - 3 ( multiply both sides by (d + 3) )
- 5d + 6 = - 3(d + 3)
- 5d + 6 = - 3d - 9 ( add 3d to both sides )
- 2d + 6 = - 9 ( subtract 6 from both sides )
- 2d = - 15 ( divide both sides by - 2 )
d = 7.5

The price of an apple is $1.25. If you get 20% discount, how much do you have to pay?
Answers
Discount 20% (0.20)
1.25 x 0.20 = 0.25
You don’t pay 0.25 so
1.25 - 0.25 = 1
You have to pay $1.
The area of a parallelogram is given by 4x² + 2x - 2. If the height is 2x
expression for the base. (area of parallelogram = bh)
2x + 2
2x - 2
2x² - 2
2x² + 2

Answers
Answer:b
Step-by-step explanation:
Jumps has $55 in her savings account. This is $21 more than David. Write and solve an equation to find the amount David has in his savings account.
(with a variable plz)
Answers
Answer:
D = $34
Step-by-step explanation:
Let's use J to represent Jumps' savings, and D to represent David's savings.
J = $55
We know David's savings is equal to 21 less than Jumps'.
This means that if we subtract 21 from 55, we will have David's savings.
D = 55 - 21
Now, solve:
D = 34
This means David has $34 in savings.
PLEASE HELP THIS IS SO IMPORTANT

Answers
Answer:
1. is moving to the left by 4 and 2. is moving up by 4
Step-by-step explanation:
a good way to get a small standard error is to use a ________.
Answers
Answer: A good way to get a small standard error is to use a large sample.
Step-by-step explanation:
In order to find the small standard error, there is always need of a complete set which is called the large sample.
If tried to do a small or repeating sample, you will most likely not get an error and you could get a repetition. If you do a population sample, you wont get accurate results at all.
Therefore, a good way to get a small standard error is to use a large sample. Hope this helps!
-From a 5th Grade Honors Student
how fast is the angle between the ladder and the ground changing in example 2 when the bottom of the ladder is 6 ft from the wall?
Answers
The angle between the ladder and the ground is - 0.075 rad/s.
Pythagoras' theorem is a essential relation in Euclidean geometry among the 3 facets of a proper triangle. It states that the region of the rectangular whose aspect is the hypotenuse (the aspect contrary the proper angle) is identical to the sum of the regions of the squares on the alternative facets.
cosθ = x/10
On differentiating the above equation,
- sinθdθ/dt = (1/10)dx/dt
dθ/dt = -(1/10)dx/dt/sinθ
sinθ = y/10
= √(100 - 36)/10
= 0.8; dθ/dt
= -(1/10)·0.6 ft/s/0.8
= - 0.075 rad/s
To learn more about triangle check the link below:
https://brainly.com/question/17335144
#SPJ4
If P(B)=0.3,P(A∣B)=0.5,P(B ′ )=0.7, and P(A∣B ′ )=0.8, find P(B∣A).
Answers
If P(B)=0.3, P(A|B)=0.5, P(B')=0.7and P(A|B')=0.8, then the value of the probability P(B|A)= 0.2113
To find the value of P(B|A), follow these steps:
The probability of B given A can be given by the product of the probability of A given B and the probability of B, divided by the total probability of B. So, the formula for P(B|A) = P(A|B) * P(B) / [P(A|B)*P(B)+P(A|B')*P(B')]. Substituting the values, we get P(B|A) = (0.5) (0.3) / [(0.5) (0.3) + (0.8) (0.7)] ⇒P(B|A) = 0.15 / [0.15 + 0.56] ⇒P(B|A) = 0.15 / 0.71 ⇒P(B|A) = 0.2113. Therefore, P(B|A) = 0.2113.Learn more about probability:
brainly.com/question/13604758
#SPJ11
Problem 10: Two bankers each arrive at the station at some random time between 5:00 AM and 6:00AM (arrival time for either banker is uniformly distributed). They stay exactly five minutes and then leave. What is the probability they will meet on a given day
Answers
If two bankers each arrive at the station at some random time between 5:00 AM and 6:00AM and stay exactly five minutes and then leave, then the probability they will meet on a given day is 84.03%.
Let the two bankers be A and B. For the two bankers to meet, they must be at the station at the same time. The probability of this happening is equal to the probability that the time between their arrivals is less than or equal to five minutes. We can solve this problem by using geometric probability.
Let x be the number of minutes past 5:00 AM that banker A arrives, and let y be the number of minutes past 5:00 AM that banker B arrives. Then x and y are both uniformly distributed on the interval [0,60], since the arrival time for either banker is uniformly distributed.
To find the probability they will meet on a given day, we need to find the probability that |x−y|≤5.
We can represent this condition geometrically as follows:
This is a square of side length 60 units with area 3600 square units. The shaded region is the set of points (x,y) such that |x−y|≤5. This region consists of two right triangles of base 55 and height 55.
The area of each triangle is 1/2 * base * height = 1/2 * 55 * 55 = 1512.5 square units.
The area of the shaded region is therefore 2 * 1512.5 = 3025 square units.
The probability that the two bankers will meet on a given day is equal to the area of the shaded region divided by the area of the square, or 3025/3600 = 0.8403 (rounded to four decimal places).
Therefore, the probability they will meet on a given day is 0.8403 or 84.03%.
Learn more about Probability:
https://brainly.com/question/25839839
#SPJ11
8-2. Skills Practice. Multiplying a Polynomial by a Monomial.
Answers
To multiply a polynomial by a monomial, you must first identify the terms in the polynomial, as well as the factors in the monomial. Once you have identified the components, use the distributive property to multiply each term of the polynomial by the monomial. Then, combine like terms and simplify the resulting polynomial.
For example:
To multiply 3x2 + 2x - 5 by 2x, you would use the distributive property to multiply each term of the polynomial by the monomial: 3x2 * 2x = 6x3, 2x * 2x = 4x2, and -5 * 2x = -10x. The resulting polynomial is 6x3 + 4x2 - 10x.Learn more about Polynomial: https://brainly.com/question/24662212
#SPJ4
An ice cream cone is 4 in across and 6 in deep. A scoop of ice cream with a diameter of 4 inches is placed on top. If the ice cream completely melts, how much ice cream spills out of the cone? Round answer to two decimal places.
Answers
Answer:
8.373
Step-by-step explanation:
Cone
Find the volume of the cone
V = 1/3 pi r^2 h
r = d/2
r = 4/2
r = 2 inches
h = 6 inches
pi = 3.14
V = 1/3 * 3.14 * 2^2 * 6
V = 25.12
Half sphere
V = 1/2 (4/3) pi r^3
r = 2 from above calculation
pi = 3.14
V = 2/3 * 3.14 * 2^3
V = 2/3 * 3.14 * 8
V = 16.74
Nothing spills out so I scoop must be a whole sphere. The sphere is 2 times what I calculated it to be or
V = (4/3) * 3.14 * 2^3
V = 33.49 cubic inches
The difference in volume is 33.49 - 25.12 = 8.373
Help needed ASAP will give you BRAINLIEST and 5 STARS RATE
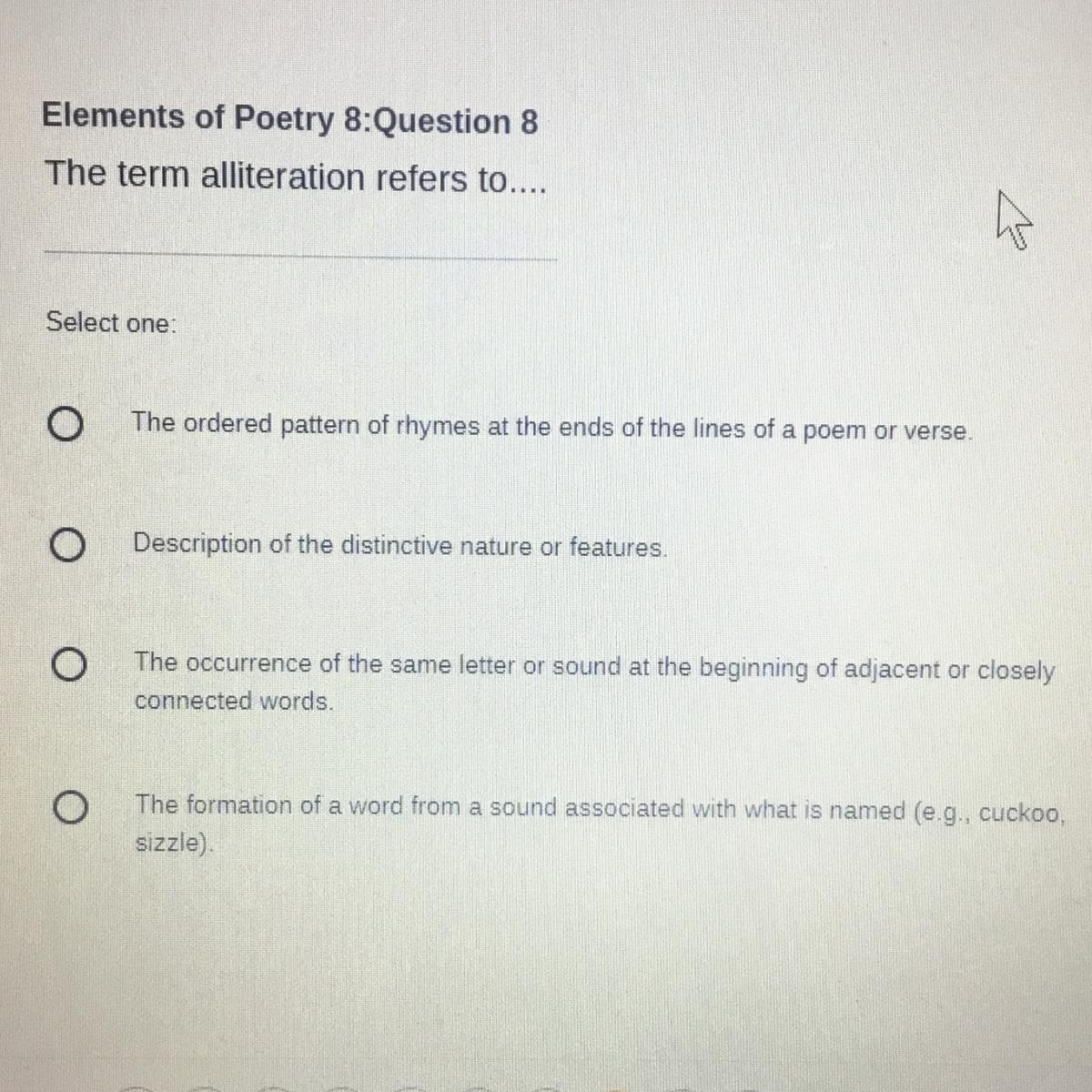
Answers
Answer:
the 3 one
Step-by-step explanation:
the occurrence of the same letter or sound at the beginning of adjacent or closely connected words.
Hope u do good on ur test or whtevr this is!!!!
ted
Explain how to find each missing digit.
Display each 0-9 tile exactly once.
If you have a partner, take turns.
Answers
Answer:
What is a partner
Step-by-step explanation:
a bucket has 10 names in it: john, jorge, samuel, abigail, deAndre, laura, rebecca, adam, and kelly. one name will be pulled out randomly. find the probability of each event. write each answer as a fraction, percent, and decimal.
1. P(Kelly)=
2. P(name starting with a J)=
3. P(not Laura)=
4. P(4 letter name)=
5. P(girl)=
6. P(not a 5 letter name)=
Answers
1. P(Kelly) = 1/10 = 0.1 = 10%, 2. P(name starting with a J) = 2/10 = 1/5 = 0.2 = 20%, 3. P(not Laura) = 8/10 = 4/5 = 0.8 = 80%, 4. P(4 letter name) = 2/10 = 1/5 = 0.2 = 20%, 5. P(girl) = 3/10 = 0.3 = 30%, 6. P(not a 5 letter name) = 6/10 = 3/5 = 0.6 = 60%
To find the probability of each event, we first need to determine the number of favorable outcomes and the total number of possible outcomes. In this case, the total number of possible outcomes is 10 because there are 10 names in the bucket.
For example, to find the probability of selecting Kelly (P(Kelly)), we see that there is only one favorable outcome, and there are a total of 10 possible outcomes. Therefore, P(Kelly) = 1/10.
Similarly, to find the probability of selecting a name starting with a J (P(name starting with a J)), we count the number of names that start with a J (which is 2) and divide by the total number of possible outcomes (which is 10).
Finally, we express each probability as a fraction, percent, and decimal for ease of comparison and understanding.
to learn more about probability click here: brainly.com/question/30034780
#SPJ11