What is the value of the expression 5 5/12-3 1/4
Answers
Answer:
\( \boxed{ \bold{2 \frac{1}{6} }}\)
Step-by-step explanation:
\( 5\frac{5}{12} \: - \: 3 \frac{1}{4} \)
It must be subtracted separately because on the one hand they are whole numbers and on the other mixed numbers.\((5 \: - \: 3) \: + \: ( \frac{5}{12} \: - \: \frac{1}{4} )\)
Mixed and whole numbers are subtracted and remain like this.\(2 \: + \: \frac{1}{6} \)
We interpret it in a mixed number (fraction).\( \boxed{ \bold{2 \frac{1}{6} }}\)
MissSpanishAnswer:
\(2\frac{1}{6}\)
Step-by-step explanation:
\(5\frac{5}{12} -3\frac{1}{4}\)
First, make these two fractions mixed numbers.
\(\frac{65}{12} -\frac{13}{4}\)
Now multiply the numerator and denominator by 3 in 13/4 to make the denominators equal.
\(\frac{65}{12} -\frac{13*3}{4*3}\)
\(\frac{65}{12} -\frac{39}{12}\)
Now subtract the fractions.
\(\frac{65-39}{12} \\\\\frac{26}{12}\)
Now write the answer as a mixed number.
\(2\frac{2}{12}\)
To simplify the answer divide numerator and denominator by 2.
\(2\frac{1}{6}\)
Related Questions
which of the following expression eqaul to -4x^2-36
Answers
Answer:
2hole square and six whole square (a+b) (a-b) finish...
What are the zeroes of the function?
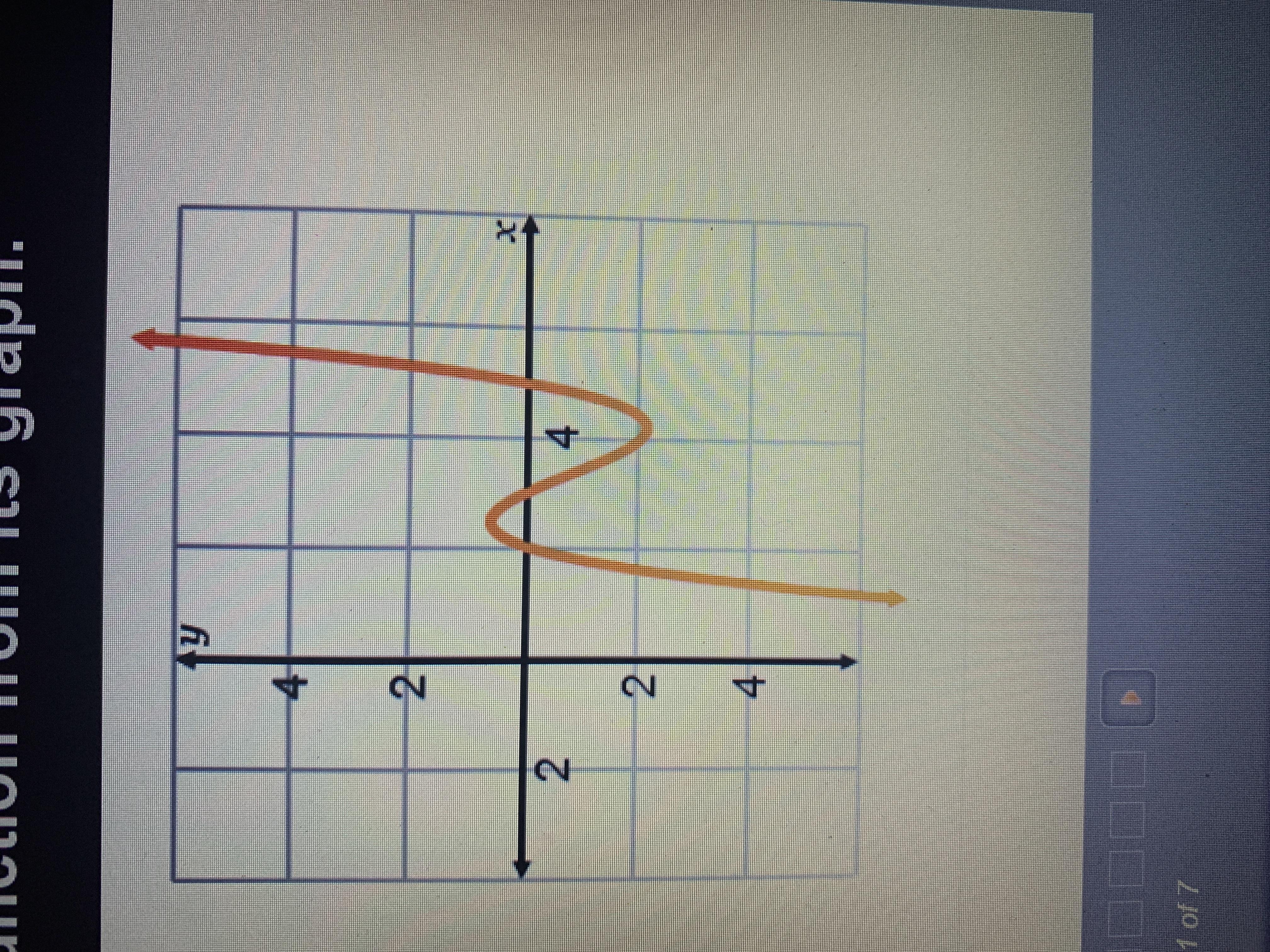

Answers
Answer:
2, 3 and 5
Step-by-step explanation:
Answer:
2,3,5
Step-by-step explanation:
Steve is going shopping. This matrix shows his shopping list:
How much will Steve spend if he shops at S2?
Round to the nearest cent

Answers
$27.71 is the amount Steve spend if he shops at S2.
Given that Steve is going shopping
The shopping list of steve has 2 cereal, 4 soups , 2 soda, 1 milk and 4 candy.
We have to find the cost spend by Steve when he purchase in shop 2, S2.
In S2, the cereal cost 2.15, soup cost 2.75, soda cost is 3.00, Milk cost 3.25 and candy costs 0.79.
Total cost = 2×2.15 + 4×2.75+2×3+1×3.25+4×0.79
=4.3+11+6+3.25+3.16
=27.71
Hence, $27.71 is the amount Steve spend if he shops at S2.
To learn more on Total cost click:
https://brainly.com/question/14927680
#SPJ1
A particle in the ocean moves with a wave. The motion of the particle can be modeled by the cosine function. If a 14 in. wave occurs every 10 s, write a function that models the height of the particle in inches y as it moves in seconds x. What is the period of the function?
Answers
The required function y = 7 cos (2π * 0.1 * x) and period of the function is 10 seconds, which is the time it takes for one complete cycle of the wave.
How to find the cosine function of this problem?he cosine function can be used to model periodic motion, and its general form is:
y = A cos (Bx + C) + D
where A is the amplitude, B is the frequency, C is the phase shift, and D is the vertical shift.
In this case, we know that a 14 in. wave occurs every 10 s, so we can use this information to find the frequency, which is the reciprocal of the period. The period is the time it takes for one complete cycle of the wave, which in this case is 10 s.
Therefore, the frequency is:
\(f = \frac{1}{T}=\frac{1}{10} = 0.1 Hz\)
We can also see that the amplitude of the wave is 7 inches, since the wave has a height of 14 inches from its highest point to its lowest point.
Now we can write the function that models the height of the particle in inches y as it moves in seconds x:
y = 7 cos (2π * 0.1 * x)
Here, the frequency is expressed in radians per second (2π * 0.1 = 0.2π), since the cosine function takes radians as its argument. The phase shift and vertical shift are both zero in this case, since the wave starts at its highest point and has no vertical shift.
Therefore, the period of the function is 10 seconds, which is the time it takes for one complete cycle of the wave.
To know more about Function visit:
brainly.com/question/28193995
#SPJ1
9. If DF = 61 and EF = 18, find DE.
10. If DE=4x-1, EF = 9, and DF = 9x-22, find
the value of x.
D
11. If DF = 78, DE = 5x-9, and EF = 2x + 10, find EF.
12. If DE= 4x + 10, EF=2x-1, and DF = 9x-15, find DF.

Answers
The obtained answers for the given line segments are as follows:
9. The value of the line segment \(\overline {DE}\) = 43; Where \(\overline { DF}\) = 61 and \(\overline {EF}\)
10. The value of x is 6; Where \(\overline {DE}\) = 4x - 1, \(\overline {EF}\) = 9, and \(\overline { DF}\) = 9x - 22
11. The value of line segment \(\overline {EF}\) = 32; Where \(\overline { DF}\) = 78, \(\overline {DE}\) = 5x - 9, and \(\overline {EF}\) = 2x + 10
12. The value of line segment \(\overline { DF}\) = 57; Where \(\overline {DE}\) = 4x + 10 \(\overline {EF}\) = 2x - 1, and \(\overline { DF}\) = 9x - 15.
What is a line segment?A line segment is a part of a line formed by infinite points with two endpoints at both ends. The line segment is represented by the two endpoints.A line segment has a finite length.Calculation:The calculation for the required values is as follows:
9. Finding \(\overline{DE}\):
It is given that,
\(\overline{DF}\) = 61; \(\overline{EF}\) = 18
From the figure, we can write
\(\overline{DF} = \overline{DE} + \overline{EF}\)
On substituting the given values,
61 = \(\overline{DE}\) + 18
⇒ \(\overline{DE}\) = 61 - 18
∴ \(\overline{DE}\) = 43
10. Finding x:
It is given that,
\(\overline {DE}\) = 4x - 1, \(\overline {EF}\) = 9, and \(\overline { DF}\) = 9x - 22
From the figure we have
\(\overline{DF} = \overline{DE} + \overline{EF}\)
On substituting,
(9x - 22) = (4x - 1) + 9
⇒ 9x - 22 = 4x - 1 + 9
⇒ 9x - 4x = 8 + 22
⇒ 5x = 30
∴ x = 6
11. Finding \(\overline{EF}\):
It is given that,
\(\overline { DF}\) = 78, \(\overline {DE}\) = 5x - 9, and \(\overline {EF}\) = 2x + 10
From the figure we have
\(\overline{DF} = \overline{DE} + \overline{EF}\)
On substituting,
78 = (5x - 9) + (2x + 10)
⇒ 78 = 5x - 9 + 2x + 10
⇒ 7x + 1 = 78
⇒ 7x = 78 - 1
⇒ 7x = 77
∴ x = 11
On substituting x = 11 in \(\overline {EF}\) = 2x + 10; we get
\(\overline {EF}\) = 2(11) + 10
= 22 + 10
= 32
Therefore, the value of the line segment \(\overline {EF}\) is 32.
12. Finding \(\overline {DF}\):
It is given that,
\(\overline {DE}\) = 4x + 10 \(\overline {EF}\) = 2x - 1, and \(\overline { DF}\) = 9x - 15
From the figure we have
\(\overline{DF} = \overline{DE} + \overline{EF}\)
On substituting,
(9x - 15) = (4x + 10) + (2x - 1)
⇒ 9x - 15 = 4x + 10 + 2x - 1
⇒ 9x - 15 = 6x + 9
⇒ 9x - 6x = 9 + 15
⇒ 3x = 24
∴ x = 8
On substituting x = 8 in \(\overline { DF}\) = 9x - 15; we get
\(\overline { DF}\) = 9(8) - 15
= 72 - 15
= 57
Therefore, the value of the line segment \(\overline { DF}\) is 57.
Learn more about line segments here:
https://brainly.com/question/280216
#SPJ9
Find the slope of the tangent line to the curve defined by 4x2+5xy+y4=370
at the point (−9,−1)
Answers
Answer:
The slope of the tangent line to the curve at the given point is -11/7.
Step-by-step explanation:
Differentiation is an algebraic process that finds the gradient (slope) of a curve. At a point, the gradient of a curve is the same as the gradient of the tangent line to the curve at that point.
Given function:
\(4x^2+5xy+y^4=370\)
To differentiate an equation that contains a mixture of x and y terms, use implicit differentiation.
Begin by placing d/dx in front of each term of the equation:
\(\dfrac{\text{d}}{\text{d}x}4x^2+\dfrac{\text{d}}{\text{d}x}5xy+\dfrac{\text{d}}{\text{d}x}y^4=\dfrac{\text{d}}{\text{d}x}370\)
Differentiate the terms in x only (and constant terms):
\(\implies 8x+\dfrac{\text{d}}{\text{d}x}5xy+\dfrac{\text{d}}{\text{d}x}y^4=0\)
Use the chain rule to differentiate terms in y only. In practice, this means differentiate with respect to y, and place dy/dx at the end:
\(\implies 8x+\dfrac{\text{d}}{\text{d}x}5xy+4y^3\dfrac{\text{d}y}{\text{d}x}=0\)
Use the product rule to differentiate terms in both x and y.
\(\boxed{\dfrac{\text{d}}{\text{d}x}u(x)v(y)=u(x)\dfrac{\text{d}}{\text{d}x}v(y)+v(y)\dfrac{\text{d}}{\text{d}x}u(x)}\)
\(\implies 8x+\left(5x\dfrac{\text{d}}{\text{d}x}y+y\dfrac{\text{d}}{\text{d}x}5x\right)+4y^3\dfrac{\text{d}y}{\text{d}x}=0\)
\(\implies 8x+5x\dfrac{\text{d}y}{\text{d}x}+5y+4y^3\dfrac{\text{d}y}{\text{d}x}=0\)
Rearrange the resulting equation in x, y and dy/dx to make dy/dx the subject:
\(\implies 5x\dfrac{\text{d}y}{\text{d}x}+4y^3\dfrac{\text{d}y}{\text{d}x}=-8x-5y\)
\(\implies \dfrac{\text{d}y}{\text{d}x}(5x+4y^3)=-8x-5y\)
\(\implies \dfrac{\text{d}y}{\text{d}x}=\dfrac{-8x-5y}{5x+4y^3}\)
To find the slope of the tangent line at the point (-9, -1), substitute x = -9 and y = -1 into the differentiated equation:
\(\implies \dfrac{\text{d}y}{\text{d}x}=\dfrac{-8(-9)-5(-1)}{5(-9)+4(-1)^3}\)
\(\implies \dfrac{\text{d}y}{\text{d}x}=\dfrac{72+5}{-45-4}\)
\(\implies \dfrac{\text{d}y}{\text{d}x}=-\dfrac{77}{49}\)
\(\implies \dfrac{\text{d}y}{\text{d}x}=-\dfrac{11}{7}\)
Therefore, slope of the tangent line to the curve at the given point is -11/7.
SOMEBODY HELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIEST
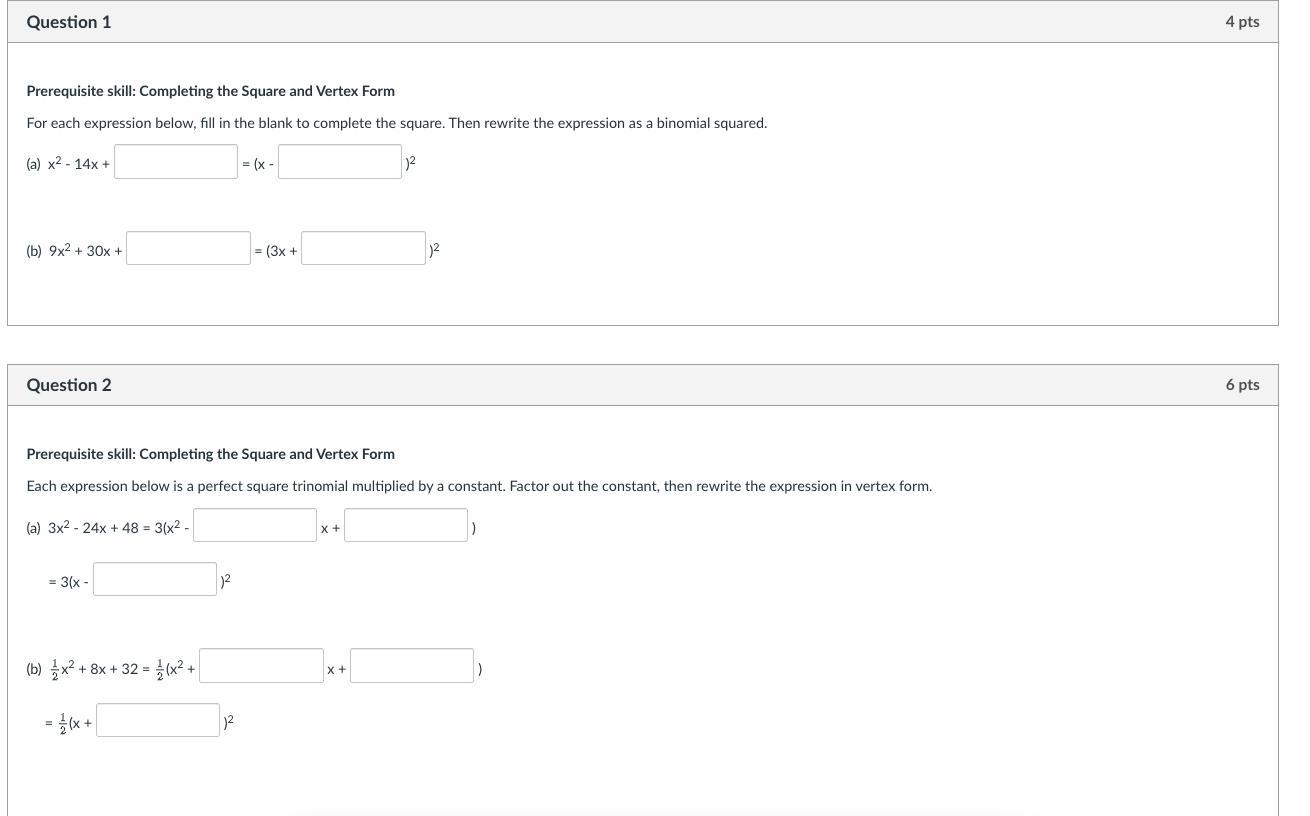
Answers
Answer:
\(\textsf{1.(a)} \quad x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
\(\textsf{1.(b)} \quad 9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\begin{aligned}\textsf{2.(a)}\quad3x^2-24x+48&=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\\&=3\left(x-\boxed{4}\right)^2\end{aligned}\)
\(\begin{aligned}\textsf{2.(b)}\quad \dfrac{1}{2}x^2+8x+32&=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\\&=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\end{aligned}\)
Step-by-step explanation:
Question 1(a) When completing the square for a quadratic equation in the form ax² + bx + c where the leading coefficient is one, we need to add the square of half the coefficient of the x-term:
\(x^2-14x+\left(\dfrac{-14}{2}\right)^2\)
\(x^2-14x+\left(-7\right)^2\)
\(x^2-14x+49\)
We have now created a perfect square trinomial in the form a² - 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Therefore:
\(a^2=x^2 \implies a=1\)
\(b^2=49=7^2\implies b = 7\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
(b) When completing the square for a quadratic equation where the leading coefficient is not one, we need to add the square of the coefficient of the x-term once it is halved and divided by the leading coefficient, and then multiply it by the leading coefficient:
\(9x^2 + 30x +9\left(\dfrac{30}{2 \cdot 9}\right)^2\)
\(9x^2 + 30x +9\left(\dfrac{5}{3}\right)^2\)
\(9x^2 + 30x +9 \cdot \dfrac{25}{9}\)
\(9x^2 + 30x +25\)
We have now created a perfect square trinomial in the form a² + 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 +2ab + b^2 = (a +b)^2}\)
Therefore:
\(a^2=9x^2 = (3x)^2 \implies a = 3x\)
\(b^2=25 = 5^2 \implies b = 5\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\hrulefill\)
Question 2(a) Factor out the leading coefficient 3 from the given expression:
\(3x^2-24x+48=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\)
We have now created a perfect square trinomial in the form a² - 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=3\left(x-\boxed{4}\right)^2\)
(a) Factor out the leading coefficient 1/2 from the given expression:
\(\dfrac{1}{2}x^2+8x+32=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\)
We have now created a perfect square trinomial in the form a² + 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2+2ab + b^2 = (a +b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\)
Step-by-step explanation:
Since ABCD is a rectangle
⇒ AB = CD and BC = AD
x + y = 30 …………….. (i)
x – y = 14 ……………. (ii)
(i) + (ii) ⇒ 2x = 44
⇒ x = 22
Plug in x = 22 in (i)
⇒ 22 + y = 30
⇒ y = 8
A ladder of length (2x+6) feet is positioned x feet from a wall. If the ladder reaches a height of (2x+4) feet along the wall. Find the longest leg.
A. 10ft
B. 24ft
C. 26ft
D. 13cm
Answers
Using the Pythagoras theorem, the longest leg has the length of 24 feet.
Given that,
A ladder of length (2x+6) feet is positioned x feet from a wall.
Height of the ladder = (2x + 6) feet
Distance of ladder from the wall = x feet
Height of the wall that the ladder is placed = (2x + 4) feet
These three lengths form s right triangle where (2x + 6) feet is the hypotenuse.
Longest leg is (2x + 4) feet
Using the Pythagoras theorem,
(2x + 6)² = (2x + 4)² + x²
4x² + 24x + 36 = 4x² + 16x + 16 + x²
4x² + 24x + 36 = 5x² + 16x + 16
x² - 8x - 20 = 0
(x - 10) (x + 2) = 0
x = 10 or x = -2
x = 2 is not possible.
So x = 10
Longest leg = 2x + 4 = 20 + 4 = 24 feet
Hence the length of the longest leg is 24 feet.
Learn more about Pythagoras theorem here :
https://brainly.com/question/343682
#SPJ1
what equation is the blue line

Answers
Hello!
the equation of the blue line is 3y + 0.5x
Can someone do #4 and #5

Answers
Answer:
First, find two points on the graph:
(x₁, y₁) = (0, 2)(x₂, y₂) = (2, 8)Slope = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1}} = \frac{8-2}{2-0} =\frac{6}{2}=3\)
16 + (-3) = 16 - 3 = 13
If f (x) = 2 x + 5 and three-halves are inverse functions of each other and StartFraction 41
Answers
The inverse of the function → f(x) = 2x + 5 is → f⁻¹(x) = (x/2) - (5/2).
What is the procedure to find inverse of function ?Inverse of a function can be calculated by following the steps mentioned below -
Step 1 - Replace {y} with {x} and vice - versa.Step 2 - Rewrite the equation by solving for {y}.Step 3 - Replace {y} with f⁻¹(x).According to the question, the equation given is as follows
y = f(x) = 2x + 5
y = 2x + 5
Replace 'y' with 'x', we get -
x = 2y + 5
Now, solve for y -
2y = x - 5
y = (x/2) - (5/2)
Replace 'y' with f⁻¹(x) -
f⁻¹(x) = (x/2) - (5/2)
Hence, the inverse of the function → f(x) = 2x + 5 is → f⁻¹(x) = (x/2) - (5/2).
To solve more questions on inverse of function, visit the link below-
brainly.com/question/28229665
#SPJ1
Which expression is equivalent to (1−sinβ)(1+sinβ)/cos2β for all values of β for which (1−sinβ)(1+sinβ)/cos2β is defined?
Select the correct answer below:
tan2β
tanβ+secβ
tanβ
sec2β
1
Answers
Using a trigonometric identity, it is found that the equivalent expression is given by 1.
What are the trigonometric identities used to solve this question?Relating sine and cosine, we have that:
\(\sin^{2}{\beta} + \cos^{2}{\beta} = 1\)
Then:
\(\cos^{2}{\beta} = 1 - \sin^{2}{\beta}\)
For the tangent, we have that:
\(\tan{\beta} = \frac{\sin{\beta}}{\cos{\beta}}\).
For the secant, we have that:
\(\sec{\beta} = \frac{1}{\cos{\beta}}\).
In this problem, the expression is:
\(\frac{(1 - \sin{\beta})(1 + \sin{\beta})}{\cos^{2}{\beta}} = \frac{1 - \sin^2{\beta}}{\cos^2{\beta}} = \frac{\cos^2{\beta}}{\cos^2{\beta}} = 1\)
More can be learned about trigonometric identities at https://brainly.com/question/7331447
#SPJ1
Identify the coordinates for point A. Type your answer in the form (# #), without spaces.

Answers
Answer:
(-4,3)
Step-by-step explanation:
Hope this helps. :)
The mean absolute deviation of Mr. Zimmerman's class is 0.46. What does this mean?
Answers
Answer:
is a measure of the average absolute distance between each data value and the mean of a data set.
three sides of triangle is x cm y cm z cm its perimeter and semi perimeter
Answers
Answer:
Step-by-step explanation:
Perimeter:
\(P=(x+y+z) \ cm\)
Semi-perimeter:
\(SP=\frac{1}{2} (x+y+z) \ cm\)
This is a algebra thing and its my homework please answer those questions

Answers
Answer:
w or x
Step-by-step explanation:
the square root of 40 is 6.3
Two vacationing families leave New York at the same time. They take 20 and 6 days, respectively, to reach their destination and return to New York. The vacationing families each take continuous trips to and from New York. How many days will pass before the two vacationing families leave New York on the same day again?
Answers
Answer:
Step-by-step explanation: evagline has 3/5 of box of nuts.she uses it to fill 6 bowls
20 POINTS!!!!!! A student is selling tickets for a concert. She keeps track of how many tickets she sells each day on a table. Which line plot shows this information?

Answers
Answer:
B i think uodate me the answer
Please awnser asap I will brainlist

Answers
They can buy 120 vans, 60 small trucks, and 80 large trucks.
How to find the number of van, small trucks and large truck needed?The truck company plans to spend 10 million on 260 vehicles. Each commercial van cost 25,000 dollars. Each small truck 50,000 dollars and each large truck 50,000 dollars. They needed twice as many van as small truck
Therefore,
let
s = number of small truck
number of van = v
let
l = number of large truck
v + s + l = 260
25,000(v) + 50,000(s) + 50,000(l) = 10,000, 000
v + 2s + 2l = 400
Hence,
v = 2s
So,
2s + 2s + 2l = 400
4s + 2l = 400
2s + s + l = 260
3s + l = 260
2s + l = 200
s = 60
l = 200 - 2(60)
l = 200 - 120
l = 80
v = 2(600 = 120
Therefore, they can buy the following:
number of small truck = 60
number of van = 120
number of large truck = 80
learn more on cost here: brainly.com/question/27903912
#SPJ1
Someone help with this equation

Answers
The answer is:
g(x + 1) = 6x + 1
g(4x) = 24x -5
Work/explanation:
To evaluate, I plug in x + 1 into the function:
\(\sf{g(x)=6x-5}\)
\(\sf{g(x+1)=6(x+1)-5}\)
Simplify
\(\sf{g(x+1)=6x+6-5}\)
\(\sf{g(x+1)=6x+1}\)
------------------
Do the same thing with g(4x)
\(\sf{g(4x)=6(4x)-5}\)
\(\sf{g(4x)=24x-5}\)
Hence, these are the answers.
rewrite 8/50 as a decimal
Answers
Answer:
0.16
Step-by-step explanation:
Its 0.16 because it would be easiest to make 8/50 into 16/100 to make it easier to turn into a decimal.
. Megan is standing 300ft from the Eiffel Tower. The Eiffel Tower is 900 ft tall.
What is Megan's angle of elevation if she looks at the top of the tower?
Answers
9514 1404 393
Answer:
about 71.6°
Step-by-step explanation:
The relevant trig function is ...
Tan = Opposite/Adjacent
Here, the "opposite" side of the right triangle is the height of the tower. The "adjacent" side is the distance to the tower. Then if the angle is x, we have ...
tan(x) = 900/300 = 3
x = arctan(3) ≈ 71.6°
Megan's angle of elevation is about 71.6°.
Answer:
Solution :-Angle required = Height of Eiffel Tower/Megan standing place × arctan
=> (900/300) × arctan
=> 3 × arctan
=> 3arctan
=> 71.6⁰
Hence,
Angle = 71.6⁰
\( \\ \)
This table represents a function.
Plot points to represent the function as a graph.
x y
-4 9
-1 3
0 1
2 -3

Answers
The graph solution of the function is attached below;
What is a solution to a system of equations? (SOLUTION GRAPHICALLY)For a solution to be solution to a system, it must satisfy all the equations of that system, and as all points satisfying an equation are in their graphs, so solution to a system is the intersection of all its equation at single point(as we need common point, which is going to be intersection of course)(this can be one or many, or sometimes none)
Given in the question;
points to be plotted;
(-4,9) , (-1,3) , (0,1) , (2,-3)
Learn more about finding the solution graphically here:
https://brainly.com/question/26254258
#SPJ1

3/4 x 2 /4 on a number line
Answers
Plot 3/8 on the number line
Select the function that represents a parabola with vertex at (2,1) and y-intercept (0,3).
Question 10 options:
A)
ƒ(x) = 1∕2(x – 2)2 + 1
B)
ƒ(x) = 1∕2(x + 2)2 + 1
C)
ƒ(x) = 2(x + 2)2 + 1
D)
ƒ(x) = 2(x – 2)2 + 1
Answers
Answer:
y - 1 = (1/2)(x - 2)^2
Step-by-step explanation:
The appropriate equation for such a parabola has the form
y - k = a(x - h)^2, where (h, k) is the vertex:
y - 1 = a(x - 2)^2. Since the y-intercept is (0, 3), we substitute 3 for y and 0 for x, obtaining:
3 - 1 = a(0 - 2)^2, or
2 = a(4). Therefore, a = 1/2, and the equation of this parabola is:
y - 1 = (1/2)(x - 2)^2
Last year, Gina's sweet potato farm produced 337 tons of sweet potatoes. This year, the sweet potato production increased by 40%. How many tons of sweet potatoes did Gina's farm produce this year? 427 tons 425 tons 447 tons 445 tons
Answers
So, Gina's farm produced approximately 471.8 tons of sweet potatoes this year. Rounded to the nearest whole number, this is 472 tons.
What you mean by increasing?When we talk about an increase, we are referring to a change in quantity or value that is greater than the original amount. In other words, an increase means that something has gotten bigger, larger, or more than it was before.
Given by the question.
To find out how much sweet potatoes Gina's farm produced this year, we need to add 40% of last year's production to the amount produced last year:
40% of 337 tons = 0.4 x 337 = 134.8 tons
Adding this to last year's production gives:
337 + 134.8 = 471.8 tons
To learn more about increase:
https://brainly.com/question/9895771
#SPJ1
Help help help please in a hurry!!!!!!!!!!!!!!!!!!!

Answers
Answer:D
Step-by-step explanation:
please mark brainliest
A christmas gift to you to earn some points
So if lucie has 1897 gifts but her friend barb has 376 more than lucie, so first subtractd barbs number of gifts by 44 and the awnser you get is how much is how much she givs to her family!!!!!
Barbs number if gifts-44=……
Answers
Answer:
2229 thanks, merry early Christmas
the weight of an apple is 150g, rounded to the nearest 5g. What is the lower bound of the weight of the apple?
What is the upper bound of the weight of the apple?
Answers
Answer:
1 answer
Answer:lower bound = 147.5gupper bound = 152.5gStep-by-step explanation:if you were rounding a single digit number to the nearest 5, ...
Step-by-step explanation:
1/2 to exponent of 4
Answers
Answer:
0.0625 is the answer.
Hope it helps you!!!