what percentage of drivers obey the law despite not knowing the law use percentages to answer round to one decimal place

Answers
Number of drivers that do not know the law = 65
Number of drivers that do not know the law but obeys the law = 50
Percentage of drivers that obey the law despite not knowing the law is
\(=\frac{50}{65}\times100percent\)
= 76.9 %
Related Questions
pls help! evaluate the sine of the real number, pls give exact answers

Answers
Answer:
\(-\frac{\sqrt2}{2} \\\) or exact is −0.70710678...
Step-by-step explanation:
Getting the point!
If we look at the unit circle and we find \(-\frac{3\pi }{4}\) we see it is in the 3rd quadrant. We know that all points in the 3rd quadrant have both negative x and negative y values. We know that all radians with the base of 4 on the unit circle have the points of \((\frac{\sqrt{2}}{2} ,\frac{\sqrt{2}}{2})\) Because we are in the 3rd quadrant and both x and y are negative we know the point of \(-\frac{3\pi }{4}\) is \((-\frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2})\)Finding the sin!
Because we know that sin is asking us for the y valueWe can just look at the point and find the y value! the y value is \(-\frac{\sqrt2}{2} \\\)Because this fraction does not need to be rationalized we are good!Use a calculator to find the exact value and you get -0.70710678...The final answer is \(-\frac{\sqrt2}{2} \\\) or exact is −0.70710678...Hope this helps!! Please mark Brainliest!
8. An arena has 5,744 seats. The seats
are divided into 16 sections with the ne
same number of seats in each section.
How many seats are in each section?
A. 349
B. 359
C. 369
D. 379
Answers
5,744 / 16 = 359
(# of total seats) / (# of sections) = (# of seats in each section)
A sales associate in a jewelry store earns $450 each week, plus a commission equal to 2% of her sales. this week her goal is to earn at least $800. how much must the associate sell in order to reach her goal
Answers
In order for the associate to meet her objective of making at least $800, she must sell at least $17,500 worth of jewelry.
To solve this problemWe must figure out how many sales are necessary to get that income.
Let's write "S" to represent the sales amount.
The associate's base pay is $450 per week, and she receives a commission of 2% of her sales. Her commission is therefore equal to 0.02S (2% of sales), which can be computed.
The total income must be at least $800 in order for her to fulfill her goal. As a result, we may construct the equation shown below:
Base Salary + Commission ≥ Goal
$450 + 0.02S ≥ $800
Now, we can solve the inequality to find the minimum sales amount:
0.02S ≥ $800 - $450
0.02S ≥ $350
Divide both sides by 0.02 to isolate 'S':
S ≥ $350 / 0.02
S ≥ $17,500
Therefore, In order for the associate to meet her objective of making at least $800, she must sell at least $17,500 worth of jewelry.
Learn more about inequality here : brainly.com/question/24372553
#SPJ1
Some of them needs to be simplify and remember it needs to be shown by Polynomials




Answers
1. A simplified expression for the volume of the above prism is 15x³ cubic units.
2. Destiny made her mistake in step 1, and the correct solution with steps is shown below.
How to calculate the volume of a rectangular prism?In Mathematics and Geometry, the volume of a rectangular prism can be calculated by using the following formula:
Volume of a rectangular prism = L × W × H
Where:
L represents the length of a rectangular prism.W represents the width of a rectangular prism.H represents the height of a rectangular prism.By substituting the given dimensions into the formula for the volume of a rectangular prism, we have the following;
Volume of rectangular prism = 3x × 5x × x
Volume of rectangular prism = 15x³ cubic units.
Question 2.
Given the following expression, \(\frac{5(x+2)-(8-x)}{2}\)
Step 1: we would open the bracket;
\(\frac{5x\;+\;10\;-\;8\;+\;x}{2}\)
Step 2: we would collect like-terms and evaluate;
\(\frac{5x\;+\;x\;+\;10\;-\;8}{2}\\\\\frac{6x\;+\;2}{2}\)
Step 3: we would split;
\(\frac{6x}{2}+ \frac{2}{2}\)
Step 4: we would divide;
3x + 1
Read more on volume of prism here: brainly.com/question/21012007
#SPJ1
What is the range of f/x )= sin x the set of all real numbers?
Answers
On solving the provided question we can say that - The Range of the given function, f(x) = sin(x) , Range = \(-1 < y < 1\)
What is Range?Range: the discrepancy between the top and bottom numbers. To get the range, locate the greatest observed value of the variable and deduct the least observed value (the minimum). The data points between the two extremes of the distribution are not taken into consideration by the range; just these two values are considered. Between the lowest and greatest numbers, there is a range. Values at the extremes make up the range. The data set 4, 6, 10, 15, 18, for instance, has a range of 18-4 = 14, a maximum of 18, a minimum of 4, and a minimum of 4.
The Range of the given function, f(x) = sin(x)
\(-1 < y < 1\)
To know more about Range visit:
https://brainly.com/question/12789483
#SPJ4
Consider two independent binomial experiments. In the first one, 94 trials had 54 successes.In the second one, 63 trials had 40 successes. Answer the following questions. Use a confidence level of 96%. Use 4 decimal places for each answer. Do not round from one part to the next when performing the calculations, though. Find the point estimate. Find the critical value. Find the margin of error. Find the confidence interval. < p 1 − p 2
Answers
The 96% confidence interval for the difference in proportions is (−0.1127, 0.3191)
To compare the proportions of success in two binomial experiments, we can use the two-sample Z-test.
Let p1 be the proportion of success in the first experiment and p2 be the proportion of success in the second experiment. We want to test the null hypothesis H0: p1 = p2 against the alternative hypothesis Ha: p1 ≠ p2.
First, we calculate the point estimate of the difference in proportions:
\(pp1 - p2 = \frac{54}{94} - \frac{40}{63} = 0.1032\)
Next, we find the critical value of the test statistic. Since the confidence level is 96%, we have alpha = 0.04/2 = 0.02 on each tail of the distribution. Using a standard normal distribution table, we find that the critical values are ±2.0537.
The margin of error is given by:
\(ME= z \sqrt{\frac{p1(1-p1)}{n1} +\frac{p2(1-p2)}{n2} }\)
where z* is the critical value, n1 and n2 are the sample sizes of the two experiments. Plugging in the values, we get:
\(ME= z \sqrt{\frac{0.5769(1-0.5769)}{94} +\frac{0.6349(1-0.6349)}{63} }= 0.2159\)
Finally, we can construct the confidence interval for the difference in proportions as:
(p1 - p2) ± ME
which gives us:
0.1032 ± 0.2159
Thus, the 96% confidence interval for the difference in proportions is (−0.1127, 0.3191).
To know more about "Confidence interval" refer here:
https://brainly.com/question/29680703#
#SPJ11
suppose that 36% of people own dogs. if you pick two people at random, what is the probability that they both own a dog? give your answer as a decimal (to at least 3 places) or fraction
Answers
Thus, the probability that two people picked at random both own a dog is 0.1296 or 1296/10000.
To solve this problem, we need to use the formula for calculating the probability of independent events: P(A and B) = P(A) x P(B).
In this case, let A be the event that the first person owns a dog and B be the event that the second person owns a dog.
We know that P(A) = 0.36, or 36% chance that the first person owns a dog. Since the events are independent, P(B) is also 0.36.
So, the probability of both events occurring (both people owning dogs) is:
P(A and B) = P(A) x P(B)
= 0.36 x 0.36
= 0.1296
This can also be expressed as a fraction:
P(A and B) = 36/100 x 36/100
= 1296/10000
Therefore, the probability that two people picked at random both own a dog is 0.1296 or 1296/10000.
Know more about the independent events:
https://brainly.com/question/27665211
#SPJ11
I need help on this math homework

Answers
Answer:
X+8+2x+127=180(Being the angle in a triangle)3x+135=1803x=180-1353x=45x=45/3x=15# The other angle are:.<A=2x=2×15=30#<B=x+8=15+8=23#Please mark me as brainlistis q(!x ) = 3x21 2x22 x23 4x1x2 4x2x3, where !x = [x1; x2; x3]t positive de nite?
Answers
To determine whether q(!x) = 3x21 2x22 x23 4x1x2 4x2x3 is positive definite, we need to check the signs of the eigenvalues of the matrix Q defined by Q_ij = ∂^2q/∂xi∂xj evaluated at !x.
Using the expression for q(!x), we can compute the Hessian matrix of q as follows:
H(q) = [6 4 0;
4 0 4;
0 4 0]
Evaluating this matrix at !x = [x1; x2; x3]t, we get:
H(q)(!x) = [6x1+4x2 4x1 0;
4x1 0 4x3;
0 4x3 0]
Next, we need to find the eigen values of this matrix. The characteristic polynomial of H(q)(!x) is given by:
det(H(q)(!x) - λI) = λ^3 - 6x1\(λ^2\)- 16x3λ
The roots of this polynomial are the eigen values of H(q)(!x). We can solve for them using the cubic formula or by factoring out λ:
λ( \(λ^2\)- 6x1λ - 16x3) = 0
Thus, we have one eigen value at λ = 0 and two others given by the roots of the quadratic equation:
\(λ^2\)- 6x1λ - 16x3 = 0
The discriminant of this quadratic is Δ = 36x\(1^2\) + 64x3, which is always non-negative since x is positive definite. Therefore, the quadratic has two real roots if and only if 6x ≥ \(1^2\)16x3, or equivalently, 3x \(1^2\) ≥ 8x3. This condition ensures that both eigenvalues are non-negative.
In conclusion, q(!x) is positive definite if and only if 3x\(1^2\)≥ 8x3.
To know more about "Matrix" refer here:
https://brainly.com/question/30752856#
#SPJ11
PLS HELP FOR BRAINLIEST!!!!!!!!!!

Answers
Answer:
I don’t know but I think is 17 units.
Step-by-step explanation:
=====================================================
Explanation:
Point M is at (4,6) and point M' is at (-4, -3) after shifting 8 units left and 9 units down.
Apply the distance formula.
\(M = (x_1,y_1) = (4,6) \text{ and } M' = (x_2, y_2) = (-4,-3)\\\\d = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}\\\\d = \sqrt{(4-(-4))^2 + (6-(-3))^2}\\\\d = \sqrt{(4+4)^2 + (6+3)^2}\\\\d = \sqrt{(8)^2 + (9)^2}\\\\d = \sqrt{64 + 81}\\\\d = \sqrt{145}\\\\d \approx 12.041595\\\\d \approx 12\\\\\)
The distance between the two points is about 12 units.
You could also use the pythagorean theorem as an alternative method.
help me on this question please

Answers
Answer:
62
Step-by-step explanation:
you have to work out the surface area of a cuboid by:
3×2=6
5×3=15
5×2=10
sum of all the areas is 31
then times it by 2 which is 62
you don t really have to pay attention to the net, apart from the 2cm because you don t want to use it twice in the calculation.
a hexadecimal number is a number written in the base 16 number system.
t
f
Answers
True. Hexadecimal numbers are written using the base 16 number system, where digits range from 0 to 9 and A to F. They are commonly used in computer systems for concise representation and easy conversion to binary.
In the hexadecimal number system, there are 16 symbols used to represent values, namely 0-9 and A-F. Each digit in a hexadecimal number represents a multiple of a power of 16.
The symbols 0-9 represent the values 0-9, respectively. The symbols A-F represent the values 10-15, respectively, where A represents 10, B represents 11, C represents 12, D represents 13, E represents 14, and F represents 15.
For example, the hexadecimal number "3F" represents the value (3 * 16^1) + (15 * 16^0) = 48 + 15 = 63 in decimal.
Similarly, the hexadecimal number "AB8" represents the value (10 * 16^2) + (11 * 16^1) + (8 * 16^0) = 2560 + 176 + 8 = 2744 in decimal.
Hexadecimal numbers are commonly used in computer systems, as they provide a convenient way to represent large binary numbers concisely. Each hexadecimal digit corresponds to a four-bit binary number, allowing for easy conversion between binary and hexadecimal representations.
for such more question on Hexadecimal numbers
https://brainly.com/question/28280312
#SPJ8
What is the value of c in the equation 3(x-8)=x+4 ?
Answers
Answer:
hey can you make a zoom so I can join
hey can you make a zoom so I can join
hey can you make a zoom so I can join
hey can you make a zoom so I can join
hey can you make a zoom so I can join
hey can you make a zoom so I can join
hey can you make a zoom so I can join
hey can you make a zoom so I can join
hey can you make a zoom so I can join
hey can you make a zoom so I can join
Step-by-step explanation:
NEED HELP ASAP!!
Use the function below to find F(3)

Answers
Since it’s F(3), you need to plug the 3 into the x. Then expand it into 1/5 times 1/5 times 1/5, which gets you 1/125
i wasnt here when we did this, please help?
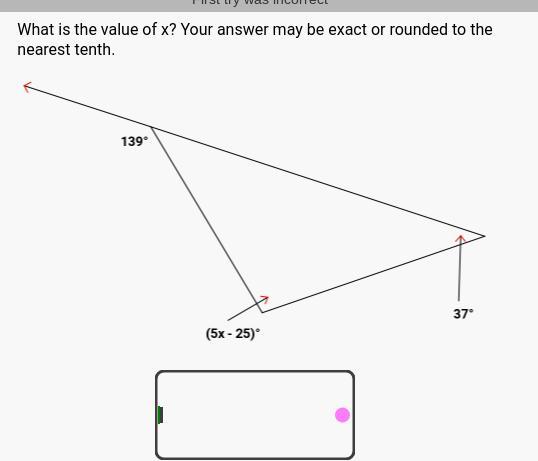
Answers
Answer:
25°
Step-by-step explanation:
look at the picture, that's the ans

Answer:
x = 25.4
Step-by-step explanation:
the exterior angle of a triangle is equal to the sum of the 2 opposite interior angles.
139° is an exterior angle of the triangle, then
5x - 25 + 37 = 139
5x + 12 = 139 ( subtract 12 from both sides )
5x = 127 ( divide both sides by 5 )
x = 25.4
Help pls!
Which rational function has zeros at x = -1 and x = 6 ?

Answers
Answer:
\(f(x) = \frac{x^{2} -5x-6}{x^{2} -4}\)
Step-by-step explanation:
Let's factorize the 1st option :
⇒ \(f(x) = \frac{x^{2} -5x-6}{x^{2} -4}\)
⇒ \(f(x) = \frac{x^{2}+x-6x-6 }{(x+2)(x-2)}\)
⇒ \(f(x) = \frac{(x+1)(x-6)}{(x+2)(x-2)}\)
===============================================================
Finding the zeros :
⇒ Factors of numerator should be equated to 0
x + 1 = 0 ⇒ x = -1x - 6 = 0 ⇒ x = 6=============================================================
Solution :
\(f(x) = \frac{x^{2} -5x-6}{x^{2} -4}\)
Answer:
first option
Step-by-step explanation:
the zeros are determined by the numerator of the rational function.
given that the zeros are x = - 1 and x = 6 , then the corresponding factors are
(x + 1) and (x - 6) , that is
(x + 1)(x - 6) ← expand using FOIL
= x² - 5x - 6
the rational function is then
f(x) = \(\frac{x^2-5x-6}{x^2-4}\)
FIND THE LCM OF EACH SET OF NUMBERS USING THE PRIME FACTORIZATION METHOD.
(BEST ANSWER = BRAINLIEST)
1. {12,15}
2. {16,24}
3. {18,27}
4. {20,28}
5. {36,54}
6. {9,12,24}
7. {15, 20, 45}
8. {6,8,12}
9. {4,6,9}
10. {8,9,12}
Answers
The LCM of the set of numbers are:
1. {12,15} = 60
2. {16,24} = 48
3. {18,27} = 54
4. {20,28} = 140
5. {36,54} = 108
6. {9,12,24} = 72
7. {15, 20, 45} = 180
8. {6,8,12} = 24
9. {4,6,9} = 36
10. {8,9,12} = 72
What is the LCM?The least common multiple of two or more numbers is the least multiple that is common to two or more numbers. A multiple of a number is the product of an integer and that number. For example, the multiples of 6 are 12 and 18.
Prime factors of 12 = 2 x 2 x 3
Prime factors of 15 = 3 x 5
LCM = 2 x 2 x 3 x 5 = 60
Prime factors of 16 = 2 x 2 x 2 x 2
Prime factors of 24 = 2 x 2 x 2 x 3
LCM = 2 x 2 x 2 x 2 x 3 = 48
Prime factors of 18 = 2 x 3 x 3
Prime factors of 27 = 3 x 3 x 3
LCM = 2 x 3 x 3 x 3 = 54
Prime factors of 20 = 2 x 2 x 5
Prime factors of 28 = 2 x 2 x 7
LCM = 2 x 2 x 5 x 7 = 140
Prime factors of 36 =2 x 2 x 3 x 3
Prime factors of 54 = 2 x 3 x 3 x 3
LCM = 2 x 2 x3 x 3 x3 = 108
Prime factors of 9 = 3 x 3
Prime factors of 12 = 2 x 2 x 3
Prime factors of 24 = 2 x 2 x 2 x 3
LCM = 2 x 2 x 2 x 3 x 3 = 72
Prime factors of 15 = 3 x 5
Prime factors of 20 = 2 x 2 x 5
Prime factors of 45 = 3 x 3 x 5
LCM = 2 x 2 x 3 x 3 x 5 = 180
Prime factors of 6 = 2 x 3
Prime factors of 8= 2 x 2 x 2
Prime factors of 12= 2 x 2 x 3
LCM = 2 x 2 x 2 x 3 = 24
Prime factors of 4 = 2 x 2
Prime factors of 6= 2 x 3
Prime factors of 9= 3 x 3
LCM = 2 x 2 x 3 x 3 = 36
Prime factors of 8 = 2 x 2 x 2
Prime factors of 9= 3 x 3
Prime factors of 12 = 2 x 2 x 3
LCM = 2 x 2 x 2 x 3 x 3 = 72
To learn more about multiples, please check: https://brainly.com/question/26030133
#SPJ1
I need some help with this one.

Answers
Answer:
B
Step-by-step explanation:
In the middle of the kite, there are 4 angles that are the same (90*)
So using the given angle 54 and the 90* we can find the last angle
54 + 90 = 144
180 - 144 = 36
The left-over angle is 36*
1/5 of 45 is what number?
Answers
If p is the incenter of triangle jkl, find each measure

Answers
Answer:
PO = 7
PM = 7
MJ = 11
∠PJO = 32°
∠KJL = 64°
PL ≈ 18.385
OL = 17
∠PLO = 22°
∠NLO = 44°
∠JKL = 72°
∠MKP = 36°
∠NKP = 36°
∠PKN = 36°
KN = 10
PL ≈ 13.04
PK ≈ 12.21
JL = 28
JK = 21
LK = 27
Step-by-step explanation:
The given parameters are;
The point representing the incenter of the triangle = P
Therefore PO = PM = PN = 7
tan(32°) = PM/JM = 7/JM
∴JM = 7/(tan(32°)) ≈ 11.2
∠PJO = tan⁻¹(7/11)≈ 32.47°
∠PJO = ∠PJM = 32° similar triangles
∠KJL = ∠KJP + ∠PJO = 32 + 32 = 64°
∠KJL ≈ 64°
PL = √(7² + 17²) ≈ 18.385
OL = NL = 17 similar triangles
∠PLO = sin⁻¹(7/18.385) ≈ 22.380°
∠PLO = ∠PLN = 22°
∠NLO = ∠PNL + ∠OLP ≈ 22° + 22° ≈ 44°
∠NLO ≈ 44.380°
∠JKL = 180 - (∠KJL + ∠NLO)
∠JKL = 180° - (64° + 44°) ≈ 72°
∠JKL ≈ 72°
∠MKP = ∠NKP = 72°/2 = 36°
∠MKP = 36°
∠NKP = 36°
∠PKN = ∠JKL - ∠MKP = 72° - 36° ≈ 36°
∠PKN ≈ 36°
KN = KM = 10
MJ = OJ = 11
PL = √(7² + 11²) ≈ 13.04
PK = √(7² + 10²) ≈ 12.21
JL = JO + OL = 11 + 17 = 28
JK = JM + MK = 11 + 10 = 21
LK = LN + NK = 17 + 10 = 27
By using the property of incenter, measures of the sides and the angles will be,
JK = 21.2 units
KL = 26.63 units
JL = 28.33 units
m∠K = 36°
By the property of incenter,
PM = PN = PO = 7 units
∠MJP = ∠OJP = 32°
∠NLP = ∠OLP = 22°
By the triangle sum theorem,
m∠JKL + m∠KLJ + m∠LJK = 180°
2(m∠NKP) + 2(m∠NLP) + 2(m∠MJP) = 180°
2(m∠NKP) + 2(22°) + 2(32°) = 180°
2(m∠NKP) = 180° - 108°
m∠NKP = 36°
From ΔJMP,
tan(32°) = \(\frac{MP}{MJ}\)
tan(32°) = \(\frac{7}{MJ}\)
MJ = \(\frac{7}{\text{tan}(32)^\circ}\)
MJ = 11.20
From ΔPOL,
tan(22°) = \(\frac{OP}{OL}\)
tan(22°) = \(\frac{7}{OL}\)
OL = 17.33
From ΔKNP,
tan(36°) = \(\frac{NP}{KN}\)
tan(36°) = \(\frac{7}{KN}\)
KN = 9.63
Therefore, JK = MJ + MK = 21.2 units
KL = LN + KN = 26.63 units
JL = JO + OL = 28.33 units
Learn more,
https://brainly.com/question/7537975
54x + 15 = -3 (3y + 1)
I need help finding the equation for y
Answers
Answer: y = -6x - 2
Step-by-step explanation:
54x + 15 = -3(3y + 1) To solve for y distribute on the right side to get,
54x + 15 = -9y -3 Add 3 to both sides
+3 +3
54x + 18 = -9y Divide each term by -9 on each side.
y = -6x - 2
Answer______
54x + 15 = -3 (3y + 1)
54x + 15 = -9y -3
+3 +3
54x + 18 = -9y
y = -6x - 2
Can someone solve all these answers for this polynomials worksheet?

Answers
Answer:
2. 4
3. 5
4. 8
5. 9
6. 1
7. 6
8. 5
9. 7
10. 2
Step-by-step explanation:
Count the number of terms for each. Alternately, count the number of "+" and "-", and add 1.
What is the y intercept function f?

Answers
Which property is illustrated?
15 + (5 + 7) = (15 + 5) + 7
plz help i will make the first on to answer with a real answer the brainiest
Answers
Answer:
associative
Step-by-step explanation:
the numbers are switched but they will equal the same thing
A jar contains 65 pennies, 27 nickels, 30 dimes, and 18 quarters. A coin is randomly selected from the jar. Find the
probability.
P (value greater than 0.15 )
Answers
The probability of randomly selecting a coin from the jar with a value greater than 0.15 is approximately 0.536, or 53.6%.
To find the probability of selecting a coin from the jar with a value greater than 0.15, we need to determine the total number of coins with a value greater than 0.15 and divide it by the total number of coins in the jar.
- Pennies: 65
- Nickels: 27
- Dimes: 30
- Quarters: 18
To find the probability, we follow these steps:
1. Count the number of coins with a value greater than 0.15:
- Pennies have a value of 0.01, so none of the pennies have a value greater than 0.15.
- Nickels have a value of 0.05, so all of the nickels have a value greater than 0.15.
- Dimes have a value of 0.10, so all of the dimes have a value greater than 0.15.
- Quarters have a value of 0.25, so all of the quarters have a value greater than 0.15.
Therefore, the total number of coins with a value greater than 0.15 is 27 (nickels) + 30 (dimes) + 18 (quarters) = 75.
2. Count the total number of coins in the jar:
The total number of coins in the jar is 65 (pennies) + 27 (nickels) + 30 (dimes) + 18 (quarters) = 140.
3. Calculate the probability:
Probability (P) = Number of favorable outcomes / Total number of possible outcomes
In this case, the number of favorable outcomes is 75 (coins with a value greater than 0.15) and the total number of possible outcomes is 140 (total number of coins in the jar).
P (value greater than 0.15) = 75 / 140 ≈ 0.536
Therefore, the probability of randomly selecting a coin from the jar with a value greater than 0.15 is approximately 0.536, or 53.6%.
Learn more about probability here
https://brainly.com/question/25839839
#SPJ11
Suppose that f(z) is analytic on {∣z∣<1} and continuous on {∣z∣≤1}. Suppose that f(z) is real-valued for all ∣z∣=1. Show that f is constant for all ∣z∣≤1. [Hint: one way to do this would be to consider g(z)=eif(z).]
Answers
If f(z) is analytic on |z| < 1, continuous on |z| ≤ 1, and real-valued for |z| = 1, then f is constant for all |z| ≤ 1.
To prove that f is constant for all |z| ≤ 1 given that f(z) is analytic on |z| < 1, continuous on |z| ≤ 1, and real-valued for |z| = 1, we can consider the function g(z) = \(e^(if(z))\)and show that g(z) is constant on |z| ≤ 1. If g(z) is constant, then f(z) must also be constant.
Let's consider the function g(z) = \(e^(if(z))\). Since f(z) is real-valued for |z| = 1, we have\(e^(if(z))\) = \(e^(if(z))\)*, where * denotes complex conjugate. Now, let's consider the modulus of g(z):
|g(z)| = \(e^(if(z))\)| = |\(e^(if(z))\)*| = \(e^(if(z))\) * \(e^(-if(z))\) = 1.
From the above equation, we can see that |g(z)| is constant for all |z| ≤ 1. According to the modulus principle, if a function is analytic in a domain and its modulus is constant in that domain, then the function itself is constant in that domain.
Therefore, since g(z) is constant for all |z| ≤ 1, it implies that f(z) is also constant for all |z| ≤ 1. Hence, f is constant for all |z| ≤ 1.
This completes the proof that if f(z) is analytic on |z| < 1, continuous on |z| ≤ 1, and real-valued for |z| = 1, then f is constant for all |z| ≤ 1.
Learn more about function here:
https://brainly.com/question/30721594
#SPJ11
Solve 2x 10 = -4
X = ?
Answers
2x • 10 = -4
20x = -4
x = - 4/20 = -0.2
Answer: x = -0.2
Please help me ASAP I need help
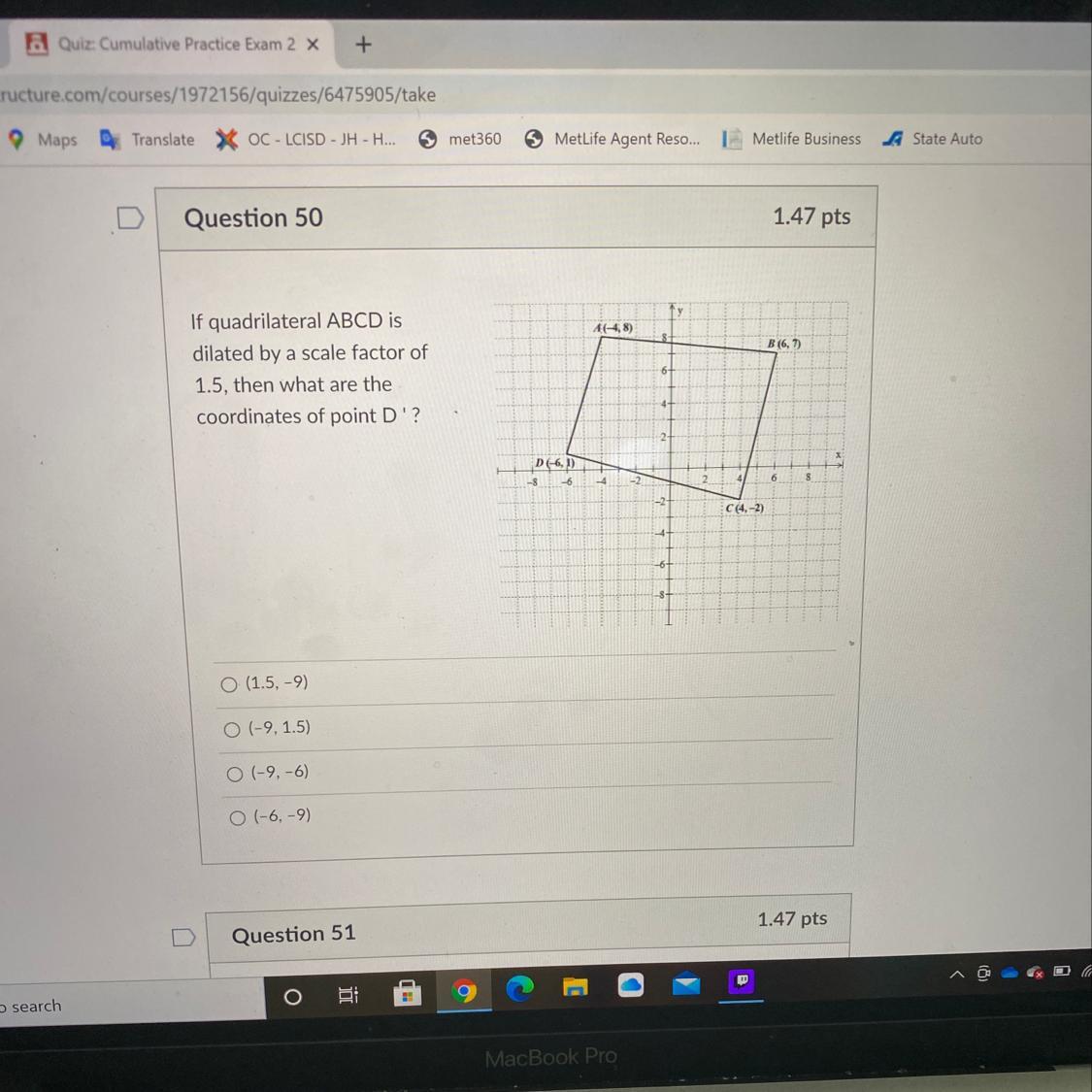
Answers
Answer:
(-9,1.5)
Step-by-step explanation:
(-6*1.5, 1*1.5)
what is the answser?

Answers
The volume of the cylinder in the diagram is 226.08 m²
How to find the volume of the prism?The volume of a cylinder of diameter D and height H is:
V = pi*(D/2)²*H
wher pi = 3.14
In the diagram we can see that the cylinder has a diameter of 6 meters and a height of 8 meters, replacing that in the formula above, we can get:
V = 3.14*(6m/2)²*8m
V = 226.08 m²
That is the volume of the cylinder.
Learn more about cylinders at:
https://brainly.com/question/9554871
#SPJ1
Answer:
V = 72π m³ (exact)
V = 226.19 m³ (approximate)
SA = 66π m² (exact)
SA = 207.34 m² (approximate)
Step-by-step explanation:
Since you don't specify what you are looking for, here are the volume and surface area.
Volume:
V = πr²h
Total Surface Area
SA = 2πr² + 2πrh
r = d/2 = 6 m / 2 = 3 m
V = πr²h
V = π × (3 m)² × 8 m
V = 72π m³ (exact)
V = 226.19 m³ (approximate)
SA = 2πr² + 2πrh
SA = 2 × π × (3 m)² + 2 × π × 3 m × 8 m
SA = (18π + 48 π) m²
SA = 66π m² (exact)
SA = 207.34 m² (approximate)
a die is continuously rolled until the total sum of all rolls exceeds 275. 275. what is the probability that at least 75 75 rolls are necessary?
Answers
The probability that at least 75 rolls are necessary to exceed a total sum of 275 is approximately 0.293.
Let X be the random variable denoting the total number of rolls required to exceed 275. We want to calculate P(X >= 75). The probability of rolling a number greater than 5 is 1/3, and the probability of rolling a number less than or equal to 5 is 2/3. Therefore, the expected value of a single roll is
(1/3)6 + (2/3)(1+2+3+4+5) = 3.67The variance of a single roll is
((1/3)2² + (2/3)(1²+2²+3²+4²+5²)) - 3.67² = 2.89.Using the properties of the geometric distribution, we can calculate the probability that it takes at least 75 rolls to achieve a sum greater than 275:
P(X >= 75) = (1 - P(X < 75)) = (1 - (1 - (275/3.67)/75\()^{(75)}\)) = 0.293.
Therefore, the probability that at least 75 rolls are required is approximately 0.293.
Learn more about Probability:
https://brainly.com/question/24756209
#SPJ4