what time is it 5 hours and 42 mins after 5:52
Answers
Answer:
11:34
Step-by-step explanation:
5:52+5=10:52
52+42=92-1 hour=1 hr and 32 mins
1 hr 32 mins+10:52=11:34
Related Questions
Write the expression as a simplified rational expression. Show your work.
5/(1/6+1/(x+1))
Answers
Answer:
30(x+1)/x+7
Step-by-step explanation:
verify the divergence theorem for the vector field and region: f=⟨4x,6z,8y⟩ and the region x2 y2≤1, 0≤z≤5
Answers
To verify the divergence theorem, we need to compute both the surface integral of the normal component of the vector field over the surface of the region and the volume integral of the divergence of the vector field over the region. If these two integrals are equal, then the divergence theorem is satisfied.
First, let's compute the volume integral of the divergence of the vector field:
div(f) = ∇ · f = ∂(4x)/∂x + ∂(6z)/∂z + ∂(8y)/∂y = 4 + 0 + 8 = 12
Using cylindrical coordinates, we can write the region as:
0 ≤ r ≤ 1
0 ≤ θ ≤ 2π
0 ≤ z ≤ 5
The surface of the region consists of two parts: the top surface z = 5 and the curved surface x^2 + y^2 = 1, 0 ≤ z ≤ 5.
For the top surface, the outward normal vector is k, and the normal component of the vector field is f · k = 8y. Thus, the surface integral over the top surface is:
∬S1 f · k dS = ∬D (8y) r dr dθ = 0
where D is the projection of the top surface onto the xy-plane.
For the curved surface, the outward normal vector is (x, y, 0)/r, and the normal component of the vector field is f · (x, y, 0)/r = (4x^2 + 8y^2)/r. Thus, the surface integral over the curved surface is:
∬S2 f · (x, y, 0)/r dS = ∬D (4x^2 + 8y^2) dA = 4∫0^1∫0^2π r^3 cos^2θ + 2r^3 sin^2θ r dθ dr = 4π/3
where D is the projection of the curved surface onto the xy-plane.
Therefore, the total surface integral is:
∬S f · n dS = ∬S1 f · k dS + ∬S2 f · (x, y, 0)/r dS = 0 + 4π/3 = 4π/3
Finally, the volume integral of the divergence of the vector field over the region is:
∭V div(f) dV = ∫0^5∫0^1∫0^2π 12 r dz dr dθ = 60π
Since the total surface integral and the volume integral are not equal, the divergence theorem is not satisfied for this vector field and region.
To learn more about divergence theorem refer below:
https://brainly.com/question/28155645
#SPJ11
why are we teching hligh levels of math at lower grades
Answers
Answer:
I have no idea
Step-by-step explanation:
people are weird
what is -3(4x-8) = -36
Answers
Answer:
x = 5
Step-by-step explanation:
-3(4x-8) = -36
Divide each side by -3
-3/-3(4x-8) = -36 /-3
4x-8 = 12
Add 8 to each side
4x-8+8 = 12+8
4x = 20
Divide each side by 4
4x/4 = 20/4
x = 5
Steps to solve:
-3(4x - 8) = -36
~Distribute
(-3 * 4x) + (-3 * -8) = -36
~Simplify
-12x + 24 = -36
~Subtract 24 to both sides
-12x + 24 - 24 = -36 - 24
~Simplify
-12x = -60
~Divide -12 to both sides
-12x/-12 = -60/-12
~Simplify
x = 5
Best of Luck!
Alan types at a rate of 30 words per minute. How many words does he type in 3 minutes? words
Answers
Answer:
90 words
Step-by-step explanation:
Based on the information we have already, we can assume Alan types the same amount of words per minute meaning, all we have to do here is multiply.
30 words per minute x 3 minutes = 90 words
Employees at a manufacturing plant have seen production rates change by approximately 105% annually. in contrast, the graph shows the change in the average annual wages of the employees. which statement accurately compares the annual change in production to the annual change in average salary
Answers
Answer:
B
Step-by-step explanation:
The annual change of protection will at some point exceed annual change in average salary. Therefore, the correct option is option B.
What is mathematical average?The ratio of the sum of the values in a particular set to all the values in the set is the mean value, which is the definition of the average. The average formula has several practical uses.
If we were asked to determine the average male height in India or the average age of the men and women in a group, we would add up all the data and divide it by the total number of data points. The annual change of protection will at some point exceed annual change in average salary.
Therefore, the correct option is option B.
To know more about mathematical average, here:
https://brainly.com/question/4769710
#SPJ2
2/9 + something =1 what is the missing number or fraction
Answers
Answer is the rest of the fraction of 1.
aka 7/9.
In this case although, if 2/9 and 7/9 was converted to decimals (0.22222222222 & 0.77777777777) then it's just be 0.99999999999.
But it should still be right until they ask for the decimal change.
Pleased to help u....

Kelly is using a compass and straightedge to perform the Geometric construction below.
Which of the following best describes the figure Kelly is constructing?

Answers
Answer:
The answer is A
Step-by-step explanation:
The line is perpendicular to RS through S
There are several constructions that can be done with the straightedge and the compass.
The statement that describes the figure Kelly is constructing is: (c) a line parallel to RS through Q
From the figure, we have the following observations
Two arcs intersect on line RSAnother set of two arcs intersect on the same level as point Q.When a line is drawn from point Q through the intersection of these lines, the line would be parallel to line RS.
Hence. we can conclude that:
Kelly is constructing (c) a line parallel to RS through Q
Read more about constructions at:
https://brainly.com/question/24706231
[Help Quick]. Fill in the table using this function rule
![[Help Quick]. Fill in the table using this function rule](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/hN5GBImU6zjGv0ocPSWVcc7Br8XFPKYH.png)
Answers
Answer:
9
15
24
33
Step-by-step explanation:
I hope this right
Question 3. Convert the following real numbers to binary (8 binary places after the radix point). (0.25 Mark) - Show your work A. 0.11 B. 0.51 C. 0.625
Answers
The binary representations are a) 0.11000110, b) 0.10000010 and c) 0.10100000.
Let's convert the given real numbers to binary with 8 binary places after the radix point.
A. 0.11:
To convert 0.11 to binary, we can use the following steps:
Multiply 0.11 by 2:
0.11 × 2 = 0.22
Take the integer part of the result, which is 0, and write it down.
Multiply the decimal part of the result by 2:
0.22 × 2 = 0.44
Again, take the integer part (0) and write it down.
Repeat steps 3 and 4 until you reach the desired precision (8 binary places after the radix point).
0.44 × 2 = 0.88 (integer part: 0)
0.88 × 2 = 1.76 (integer part: 1)
0.76 × 2 = 1.52 (integer part: 1)
0.52 × 2 = 1.04 (integer part: 1)
0.04 × 2 = 0.08 (integer part: 0)
0.08 × 2 = 0.16 (integer part: 0)
0.16 × 2 = 0.32 (integer part: 0)
0.32 × 2 = 0.64 (integer part: 0)
Write down the integer parts obtained in step 4 and 5, in order:
0.11000110
Therefore, the binary representation of 0.11 with 8 binary places after the radix point is 0.11000110.
B. 0.51:
To convert 0.51 to binary, we can use the same steps:
Multiply 0.51 by 2:
0.51 × 2 = 1.02
Take the integer part of the result, which is 1, and write it down.
Multiply the decimal part of the result by 2:
0.02 × 2 = 0.04
Again, take the integer part (0) and write it down.
Repeat steps 3 and 4 until you reach the desired precision (8 binary places after the radix point).
0.04 × 2 = 0.08 (integer part: 0)
0.08 × 2 = 0.16 (integer part: 0)
0.16 × 2 = 0.32 (integer part: 0)
0.32 × 2 = 0.64 (integer part: 0)
0.64 × 2 = 1.28 (integer part: 1)
0.28 × 2 = 0.56 (integer part: 0)
0.56 × 2 = 1.12 (integer part: 1)
0.12 × 2 = 0.24 (integer part: 0)
Write down the integer parts obtained in step 4 and 5, in order:
0.10000010
Therefore, the binary representation of 0.51 with 8 binary places after the radix point is 0.10000010.
C. 0.625:
To convert 0.625 to binary, we can use the same steps:
Multiply 0.625 by 2:
0.625 × 2 = 1.25
Take the integer part of the result, which is 1, and write it down.
Multiply the decimal part of the result by 2:
0.25 × 2 = 0.50
Again, take the integer part (0) and write it down.
Repeat steps 3 and 4 until you reach the desired precision (8 binary places after the radix point).
0.50 × 2 = 1.00 (integer part: 1)
0.00 × 2 = 0.00 (integer part: 0)
0.00 × 2 = 0.00 (integer part: 0)
0.00 × 2 = 0.00 (integer part: 0)
0.00 × 2 = 0.00 (integer part: 0)
0.00 × 2 = 0.00 (integer part: 0)
0.00 × 2 = 0.00 (integer part: 0)
0.00 × 2 = 0.00 (integer part: 0)
Write down the integer parts obtained in step 4 and 5, in order:
0.10100000
Therefore, the binary representation of 0.625 with 8 binary places after the radix point is 0.10100000.
Learn more about binary numbers click;
https://brainly.com/question/28222245
#SPJ1
In developing patient appointment schedules , a medical centre wants to estimate the mean time that a staff member spends with each patient. How large a sample should be taken if the desired margin of error is 2 minutes at a 95 per cent level of confidence? How large a sample should be taken for a 99 per cent level of confidence ? Use a planning value for the population standard deviation of 8 minutes.
Answers
A. A sample size of 62 should be taken for a 95% level of confidence.
B. The sample size of 107 should be taken for a 99% level of confidence.
a. To estimate the sample size needed to estimate the mean time a staff member spends with each patient, we can use the formula for sample size calculation:
n = (Z^2 * σ^2) / E^2
Where:
n = required sample size
Z = Z-score corresponding to the desired level of confidence
σ = population standard deviation
E = desired margin of error
For a 95% level of confidence:
Z = 1.96 (corresponding to a 95% confidence level)
E = 2 minutes
σ = 8 minutes (population standard deviation)
Substituting these values into the formula:
n = (1.96^2 * 8^2) / 2^2
n = (3.8416 * 64) / 4
n = 245.9904 / 4
n ≈ 61.4976
Since we can't have a fraction of a sample, we round up the sample size to the nearest whole number. Therefore, a sample size of 62 should be taken for a 95% level of confidence.
b. For a 99% level of confidence:
Z = 2.58 (corresponding to a 99% confidence level)
E = 2 minutes
σ = 8 minutes (population standard deviation)
Substituting these values into the formula:
n = (2.58^2 * 8^2) / 2^2
n = (6.6564 * 64) / 4
n = 426.0096 / 4
n ≈ 106.5024
Rounding up the sample size to the nearest whole number, a sample size of 107 should be taken for a 99% level of confidence.
Learn more about sample size :
brainly.com/question/25894237
#SPJ11
For what positive number is the square root of the
number the same as the number divided by 40 ?
Answers
Answer:
1600
Step-by-step explanation:
Answer:
1600Step-by-step explanation:
Let the number be x:
√x = x/40(√x)² = (x/40)²x = x²/1600x²/x = 1600x = 16000 is also a solution but we need positive integer, so its 1600
The first four terms of a sequence are shown below:
7,4, 1, -2
Which of the following functions best defines this sequence?
Of(1) = 7, f(n + 1) = f(n) + 3; for nx 1
O f(1) = 7, f(n + 1) = f(n) - 3; for nx 1
O f(1) = 7, f(n + 1) = f(n) – 4; for n 2 1
Of(1) = 7, f(n + 1) = f(n) + 4; for n > 1

Answers
Answer:
second option
Step-by-step explanation:
Given the sequence
7, 4, 1, - 2
There is a common difference d between consecutive terms, that is
d = 4 - 7 = 1 - 4 = - 2 - 1 = - 3
Thus to obtain any term in the sequence from the previous term, subtract 3
Thus
f(1) = 7 , f(n + 1) = f(n) - 3 for n ≥ 1
Which equation can be used to prove 1 + tan2(x) = sec2(x)?
StartFraction cosine squared (x) Over secant squared (x) EndFraction + StartFraction sine squared (x) Over secant squared (x) EndFraction = StartFraction 1 Over secant squared (x) EndFraction
StartFraction cosine squared (x) Over sine squared (x) EndFraction + StartFraction sine squared (x) Over sine squared (x) EndFraction = StartFraction 1 Over tangent squared (x) EndFraction
StartFraction cosine squared (x) Over tangent squared (x) EndFraction + StartFraction sine squared (x) Over tangent squared (x) EndFraction = StartFraction 1 Over tangent squared (x) EndFraction
StartFraction cosine squared (x) Over cosine squared (x) EndFraction + StartFraction sine squared (x) Over cosine squared (x) EndFraction = StartFraction 1 Over cosine squared (x) EndFraction
Answers
The equation that can be used to prove 1 + tan2(x) = sec2(x) is StartFraction cosine squared (x) Over tangent squared (x) EndFraction + StartFraction sine squared (x) Over tangent squared (x) EndFraction = StartFraction 1 Over tangent squared (x) EndFraction. the correct option is d.
How to explain the equationIn order to prove this, we can use the following identities:
tan(x) = sin(x) / cos(x)
sec(x) = 1 / cos(x)
tan2(x) = sin2(x) / cos2(x)
sec2(x) = 1 / cos2(x)
Substituting these identities into the given equation, we get:
StartFraction cosine squared (x) Over tangent squared (x) EndFraction + StartFraction sine squared (x) Over tangent squared (x) EndFraction = StartFraction 1 Over tangent squared (x) EndFraction
Therefore, 1 + tan2(x) = sec2(x).
Learn more about equations on
https://brainly.com/question/2972832
#SPJ1
Select the representations that do not change the location of the point (6, 170°). a. (-6, 350°) b. (-6, 190°) c. (-6, -10°) d. (6, -190°)
Answers
Answer:
b) (_6,198,) 1112334dccfsshh
Simplify the expression.
2x + 5(2 + 6x) + 3(2x – 7) Identify the properties you use.
Answers
Hey there!
2x + 5(2 + 6x) + 3(2x - 7)
DISTRIBUTE
= 2x + 5(2) + 5(6x) + 3(2x) - 7
= 2x + 10 + 6x + 6x - 7
COMBINE the LIKE TERMS
= (2x + 6x + 6x) + (10 - 7)
= 2x + 6x + 6x + 10 - 7
= 8x + 6x + 10 - 7
= 14x + 3
Therefore, your answer is: 14x + 3
Good luck on your assignment & enjoy your day!
~Amphitrite1040:)
jack and jill each had a summer job. jack earned $10.00 per day. jill earned 1 cent on the first day, 2 cents on the second day, 4 cents on the third day, 8 cents on the fourth day, and so on, doubling the amount she makes each day.
Answers
As per given data, Jack's total earnings over "n" days: $\(10.00 * n\)
Jill's total earnings over "n" days:\(\frac{ ((2^n - 1) cents)}{100}\).
It seems like Jack earned a fixed amount of $10.00 per day, while Jill's earnings doubled each day. To find out how much Jill earned in total, we can calculate the sum of her earnings over a given period.
Let's assume the period for both Jack and Jill is "n" days.
For Jack, his earnings are constant at $\(10.00\) per day. Therefore, his total earnings over "n" days would be:
Jack's earnings = $\(10.00 * n\)
For Jill, her earnings are doubling each day. We can observe that her earnings form a geometric progression with a common ratio of 2. Her earnings on each day can be calculated using the formula for the sum of a geometric series:
Jill's earnings on day 1 = 1 cent = $0.01 (given)
Jill's earnings on day 2 = 2 cents = $0.02
Jill's earnings on day 3 = 4 cents = $0.04
Jill's earnings on day n = 2^(n-1) cents
Jill's total earnings over "n" days can be calculated using the formula for the sum of a geometric series:
Jill's earnings = (1 cent) + (2 cents) + (4 cents) + ... + (2^(n-1) cents)
= (2^n - 1) cents
To convert Jill's total earnings from cents to dollars, we divide by 100:
Jill's total earnings = \(\frac{((2^n - 1) cents)}{100}\)
So, in summary:
Jack's total earnings over "n" days: $10.00 × n
Jill's total earnings over "n" days:\(\frac{ ((2^n - 1) cents)}{100}\)
Keep in mind that if you have a specific value for "n" (the number of days), you can substitute it into the formulas to calculate the exact earnings for both Jack and Jill.
Learn more about geometric series here:
https://brainly.com/question/30264021
#SPJ11
Q1 ***Open Data1 Population average for social conservatism is M=5.40 Effect size for the variable of social conservatism is d = 0.4 2) Is your data normally distributed? Report. 4p
Answers
We need additional information, such as a dataset or summary statistics to perform a normality test.
To determine if the data is normally distributed, we need to look at the distribution of the variable of interest. In this case, we are interested in the distribution of social conservatism scores.
If we have access to the data, we can use statistical tests such as the Shapiro-Wilk test or the Kolmogorov-Smirnov test to determine if the data is normally distributed. However, since we only have information about the population average and effect size, we cannot directly test for normality.
However, based on the central limit theorem, we can assume that if the sample size is large enough (typically >30), the distribution of the variable of interest will be approximately normal. In this case, since we do not have information about the sample size, we cannot definitively say if the data is normally distributed.
In summary, without more information about the sample size or access to the data, we cannot determine if the data is normally distributed.
To know more about the central limit theorem visit:
https://brainly.com/question/30760826
#SPJ11
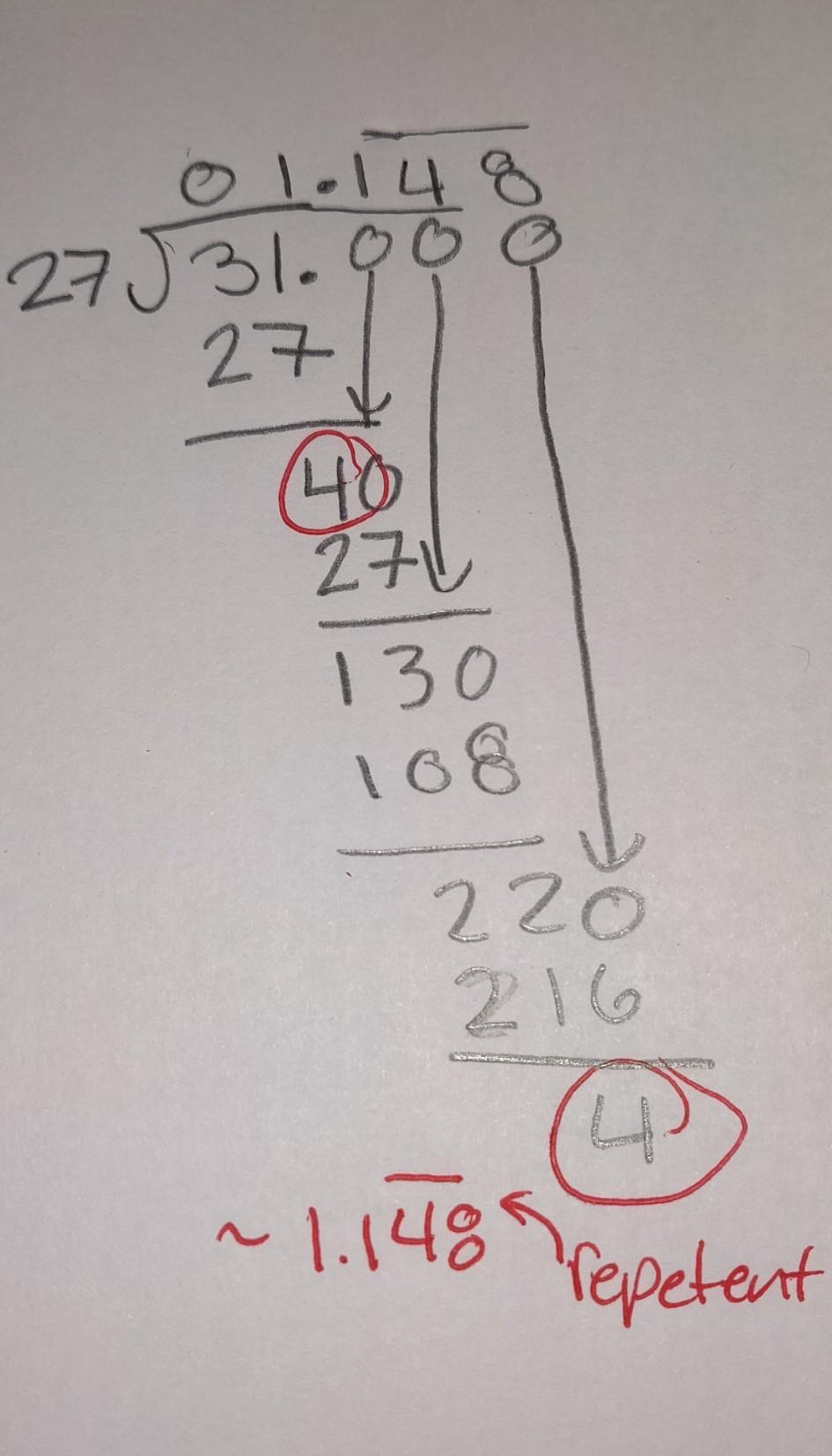
Solve with long division method 31/27
Answers
Answer:
1.148 repetent
Step-by-step explanation:
hope this helps
compute the critical value z a/2 that corresponds to 97% level of confidence, compute the critical value z a/2 that corresponds to 80% level of confidence?
Answers
The critical value z a/2 that corresponds to a 97% level of confidence is 1.96, and the critical value z a/2 that corresponds to an 80% level of confidence is 1.28.
In statistical hypothesis testing, the critical value is the point beyond which we reject the null hypothesis. To find the critical values, we need to use the standard normal distribution table or calculator.
For a 97% level of confidence, the significance level (α) is 0.03, and the critical value can be found by dividing α by 2 to get 0.015 (since it's a two-tailed test), and then finding the corresponding z-value using the standard normal distribution table or calculator. The z-value is 1.96.
Similarly, for an 80% level of confidence, the significance level (α) is 0.20, and the critical value can be found by dividing α by 2 to get 0.10 (since it's a two-tailed test), and then finding the corresponding z-value using the standard normal distribution table or calculator. The z-value is 1.28.
For more questions like Z-score click the link below:
https://brainly.com/question/15016913
#SPJ11
Pleaseeeeeeee help me

Answers
Answer:
The answer is "The discriminant is positive"
Step-by-step explanation:
When the discriminant is positive there is two real solutions.
When the discriminant is equal to 0, there is one real solution.
When the discriminant is negative, there is no real number solutions.
60 points! Please answer fast and show your work... Thank you!
You would like to purchase the car in 2 years. How much money will you need to invest at a 3.3% interest rate compounded annually in order to have $9500 in 2 years? Use the compound interest formula A = P (1 + i)n. (Round final answer to the nearest cent, but otherwise don’t round any intermediate values)
Answers
Answer:
$ 8902.72
Step-by-step explanation:
We would like to calculate the money which we need to invest at 3.3% rate compounded annually for two years . We know that ,
\(\longrightarrow \boldsymbol{ A = P \bigg(1+\dfrac{R}{100}\bigg)^n } \)
where the symbols have their usual meaning . So here ,
Amount = $ 9500 time = 2 years Rate = 3.3% P = The money we need to invest (?)\(\longrightarrow \$ 9500 = P \bigg( 1+\dfrac{3.3}{100}\bigg)^2\\ \)
Simplify RHS ,
\(\longrightarrow \$ 9500 = P \bigg(\dfrac{100+3.3}{100}\bigg)^2\\\)
Simplify Nr . in RHS ,
\(\longrightarrow \$ 9500 =P\bigg(\dfrac{103.3}{100}\bigg)^2\\ \)
Isolate P ,
\(\longrightarrow P = \dfrac{ \$9500\times 100\times 100}{103.3\times 103.3}\\\)
Simplify ,
\(\longrightarrow \underline{\underline{\boldsymbol{ P = \$ 8902.72 }}}{} \)
And we are done !
\(\bold{Formula: A = P(1 + \frac{r}{100})^{(n)}}\)
Where
A = AmountP = PrincipalR = RateN = time compounded\( \bold{Solution : } \\ \\ \: \: \: \: \tt \: A = 9,500(1+\frac{3.3\%}{100})^{(2)} \\ \: \: \: \: \: \: \tt \: A = 9,500(1+ 0.033)^{(2)} \\ \tt \: A = 9,500(1.033)^{(2)} \: \: \\ \tt \: A = 10,137.34 \qquad \: \: \: \)
therefore,I need $10,137.34 if would like to purchase the car.
How do you determine whether the sequence a_n=(2^n+3^n) / (2^n−3^n) converges, if so how do you find the limit?
Answers
You determine the limit by \(\lim_{n \to \infty} a_n = -1\).
A limit in mathematics is a point at which a function approaches the output for the specified input values. Calculus and mathematical analysis depend on limits, which are also used to determine integrals, derivatives, and continuity. The concept of limit, which is founded on the idea of closeness, is largely used to give values to some functions at points when none are defined in a way that is consistent with values close by.
Divide the denominator and numerator by 3n as shown.
\(\lim_{n \to \infty} a_n = \lim_{n \to \infty} \frac{2^n+3^n}{2^n-3^n\\}\)
\(= \lim_{n \to \infty} \frac{(\frac{2}{3})^n+1 }{(\frac{2}{3})^n-1 } \\=\frac{0+1}{0-1} \\=-1\)
To learn more about limits, refer:-
https://brainly.com/question/12211820
#SPJ4
what is the interquartille range of the given data set
11, 12, 14, 15. 18. 19. 21, 23. 25, 55
A. 25
B. 9
C. 44
Answers
Answer: B. 9
Step-by-step explanation:
First, find the median of the data set. This set has an even number of points, so find the average between the two middle points: 18 and 19. 18+19 = 37. 37/2 = 18.5. The median is 18.5.
Now, to find the lower quartile, find the median of the lower half of the data set {11, 12, 14, 15, 18}. The number in the middle is 14. The lower quartile is 14.
To find the upper quartile, find the median of the upper half of the data set {19, 21, 23, 25, 55}. The number in the middle is 23. The upper quartile is 23.
To find the interquartile range, subtract the lower quartile from the upper quartile. 23-14 = 9. The interquartile range is 9.
Problem 20:
Find d.
2dº
98°
(2d+ 2)°
Answers
The value of d if, The measure of the angles of a triangle are 2dº, 98°, and (2d+ 2)°, is 20.
What is triangle?Three straight lines coming together create a triangle. There are three sides and three corners on every triangle (angles). A triangle's vertex is the intersection of two of its sides. Any one of a triangle's three sides can serve as its base, however typically the bottom side is used.
Given:
The measure of the angles of a triangle are 2dº, 98°, and (2d+ 2)°,
Calculate the value of d as shown below,
2d + 98 + 2d +2 = 180 (The sum of the interior angle of the triangle is 180)
Do arithmetic operations as shown below,
4d + 100 = 180
4d = 180 - 100
4d = 80
d = 80 / 4
d = 20
Thus, the value of d is 20.
To know more about Triangles:
https://brainly.com/question/16886469
#SPJ1
b. What's the probability a customer who ordered pancakes came to the diner late?
c. Are breakfast choice and meal time independent? Explain.

Answers
Answer:
b. To find the probability a customer who ordered pancakes came to thediner late, we need to look at the intersection of the "pancakes" row and the "late" column. This gives us a probability of 0.1, or 10%
c. To determine whether breakfast choice and meal time are independent, we need to see if the probability of one event changes based on the occurrence of the other event. In this case, it seems that breakfast choice and meal time are not independent, as the probability of being late seems to differ based on what breakfast item the customer chose. For example, the probability of being late is higher for customers who ordered pancakes compared to those who ordered cereal. Therefore, the choice of breakfast item appears to be related to the probability of being late, and so breakfast choice and meal time are not independent.
Step-by-step explanation:
a teacher attempts to make a number cube unfair by drilling out the spots on one side and inserting lead weights. to determine if she was successful, she rolls the number cube 50 times and keeps track of the number of times she rolls a 1. she rolls a 1 15 times. she would like to know if the data provide convincing evidence that the proportion of rolls that will land on a 1 is greater than one-sixth. are the conditions for inference met? yes, the conditions for inference are met. no, the 10% condition is not met. no, the large counts condition is not met. no, the randomness condition is not met.
Answers
Yes, the conditions for inference are met. The teacher conducts 50 trials, which is large enough to meet the large counts condition (np ≥ 10 and n(1-p) ≥ 10).
The teacher's attempt to make the number cube unfair by inserting lead weights raises the question of whether the proportion of rolls that will land on a 1 has changed. To determine if she was successful, the teacher rolls the cube 50 times and keeps track of the number of times she rolls a 1. The data shows that she rolled a 1 15 times.
To determine if the data provides convincing evidence that the proportion of rolls that will land on a 1 is greater than one-sixth, we need to check if the conditions for inference are met.
The 10% condition requires that the sample size is less than 10% of the population size. Since we do not know the population size, we cannot determine if this condition is met.
The large counts condition requires that both the number of successes (15) and the number of failures (35) are greater than or equal to 10. This condition is met.
The randomness condition requires that the sample is random. Since the teacher rolled the cube, it is assumed that the rolls were random.
Therefore, the conditions for inference are met. We can use a hypothesis test to determine if the data provides convincing evidence that the proportion of rolls that will land on a 1 is greater than one-sixth.
More on inference: https://brainly.com/question/30267509
#SPJ11
find the directional derivative of the function at the given point in the direction of the vector v. f(x, y) = 3ex sin(y), (0, /3), v = −5, 12 dvf(0, /3) =
Answers
The directional derivative of the function f(x, y) = 3ex sin(y) at the point (0, π/3) in the direction of the vector v = (-5, 12) is ∂vf(0, π/3) = -60eπ/3.
The directional derivative measures the rate at which a function changes at a given point in a specific direction. To compute it, we need to take the dot product between the gradient vector (∇f) and the unit vector in the direction of v.
First, we need to find the gradient of f(x, y) by taking the partial derivatives with respect to x and y. The partial derivative with respect to x is ∂f/∂x = 3ex sin(y), and the partial derivative with respect to y is ∂f/∂y = 3ex cos(y).
Next, we evaluate the gradient at the point (0, π/3) by substituting x = 0 and y = π/3 into the partial derivatives. We obtain ∂f/∂x = 3e^0 sin(π/3) = (3/2)√3 and ∂f/∂y = 3e^0 cos(π/3) = (3/2).
To find the directional derivative, we take the dot product between the gradient vector (∇f) and the unit vector in the direction of v, which is v/|v|. Since v = (-5, 12), we normalize it to obtain the unit vector (-5/13, 12/13).
Finally, we compute the directional derivative as ∂vf(0, π/3) = (∇f) · (v/|v|) = [(3/2)√3, (3/2)] · (-5/13, 12/13) = -60eπ/3. Therefore, the directional derivative of f(x, y) at (0, π/3) in the direction of v is -60eπ/3.
Learn more about gradient vector here:
https://brainly.com/question/29751488
#SPJ11
PLZZZZZZZZZZZZZ HELP ASAP I DONT HAVE MUCH TIME!!!!!!!!!
Exit
The graph below shows the number of points each team scored. How many more points did the Marlins have than the Torpedoes?
A. 250
B. 300
C. 350
D. 450

Answers
Answer: 15
Step-by-step explanation:
Hi!
The answer is a 250
PLEASE HELP: Find the measure of the angle indicated. Arc BC is 80 degrees.
20
40
60
80
