Answers
Answer:
pi/0.25
Step-by-step explanation:
pi/0.25 = 12.5663
Related Questions
solve the equation 3|3 - 5r|- 3 = 18
Answers
Answer:
r = 2
Step-by-step explanation:
3|3 - 5 * 2|- 3 = 18
3|3 - 10| - 3 = 18
3 * 7 - 3 = 18
21 - 3 = 18
18 = 18
(Since there are absolute value signs, the answer to |3 - 5r| will be positive)
Answer:
r=0.8
Step-by-step explanation:
3|3-5r|-3=18
9-15r -3=18
6-15r=18
15r=12
r=0.8

Graph the segment with endpoints (-4, -3) and (3,5) and its image after a reflection in the line y=x.

Answers
Answer:
Step-by-step explanation:
Endpoints of the segment are (-4, -3) and (3, 5).
Rule for the reflection of the points across a line \(y=x\) is,
(x, y) → (y, x)
By following this rule of reflection,
New endpoints will be,
(-4, -3) → (-3, -4)
(3, 5) → (5, 3)
Therefore, new endpoints of the reflected segment are (-3, -4) and (5, 3).

if a = 7 and b = 2 find the value of (a - 3) squared
Answers
Step-by-step explanation:
a = 7
(a - 3)² = (7 - 3)² = (4)² = 16
what is binomial theorem calculator
Answers
A binomial theorem calculator is an online tool that calculates the expansion of a binomial expression raised to a power
The binomial theorem, also known as the binomial expansion, describes the algebraic expansion of a binomial expression, which is a mathematical expression that consists of two terms. A binomial theorem calculator is an online tool or a software program that calculates the expansion of a binomial expression raised to a power. The binomial theorem calculator can quickly and easily perform this expansion for any given binomial expression and power.
For example, if we have the binomial expression (a + b) raised to the power of 3, the binomial theorem calculator will provide the expanded form:
(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3
This expansion can be useful in many mathematical calculations and applications, such as probability theory, combinatorics, and algebraic equations.
Learn more about binomial theorem here
brainly.com/question/27813780
#SPJ4
Can someone help me solve this ???

Answers
Answer:
y = 4 x = 12
Step-by-step explanation:
The blue square I started on my own and ended with a calculator
You may need to use the appropriate appendix table or technology to answer this question. The following results are for independent random samples taken from two populations. Sample 1 Sample 2 n1 = 20 n2 = 30 x1 = 22.8 x2 = 20.1 s1 = 2.2 s2 = 4.6 (a) What is the point estimate of the difference between the two population means? (Use x1 − x2. ) 2.7 (b) What is the degrees of freedom for the t distribution? (Round your answer down to the nearest integer.) (c) At 95% confidence, what is the margin of error? (Round your answer to one decimal place.) (d) What is the 95% confidence interval for the difference between the two population means? (Use x1 − x2. Round your answers to one decimal place.)
Answers
a). The difference between the two population means is estimated at a location to be 2.7.
b). 49 different possible outcomes make up the t distribution. The margin of error at 95% confidence is 1.7.
c). The range of the difference between the two population means' 95% confidence interval is (0.0, 5.4).
d). The (0.0, 5.4) represents the 95% confidence interval for the difference among the two population means.
What is standard deviations?The variability or spread in a set of data is commonly measured by the standard deviation. The deviation between the values in the data set and the mean, or average, value, is measured. A low standard deviation, for instance, denotes a tendency for data values to be close to the mean, whereas a high standard deviation denotes a larger range of data values.
Using the equation \(x_1-x_2\), we can determine the point estimate of the difference between the two population means. In this instance, we calculate the point estimate as 2.7 by taking the mean of Sample
\(1(x_1=22.8)\) and deducting it from the mean of Sample \(2(x_2=20.1)\).
With the use of the equation \(df=n_1+n_2-2\), it is possible to determine the degrees of freedom for the t distribution. In this instance, the degrees of freedom are 49 because \(n_1\) = 20 and \(n_2\) = 30.
We must apply the formula to determine the margin of error at 95% confidence \(ME=t*\sqrt[s]{n}\).
The sample standard deviation (s) is equal to the average of \(s_1\) and \(s_2\) (3.4), the t value with 95% confidence is 1.67, and n is equal to the
average of \(n_1\) and \(n_2\) (25). When these values are entered into the formula, we get \(ME=1.67*\sqrt[3.4]{25}=1.7\).
Finally, we apply the procedure to determine the 95% confidence interval for the difference between the two population means \(CI=x_1-x_2+/-ME\).
The confidence interval's bottom limit in this instance is \(x_1-x_2-ME2.7-1.7=0.0\) and the upper limit is \(x_1+x_2+ME=2.7+1.7=5.4\).
As a result, the (0.0, 5.4) represents the 95% confidence interval for the difference among the two population means.
To know more about standard deviations click-
brainly.com/question/475676
#SPJ1
Is this congruent or not congruent? And is this
SSS
SAS
SSA
AAS
ASA
HL
PLEASE HELP, I will brainliest u

Answers
Answer: Answer is SSS ok
The average number of people who attended football games at a stadium increased from 8,000 people in the year 2005 to 12,500 in the year 2012. By what percentage did the average number of people at the games increase from 2005 to 2012?
Answers
56.1% is the average number of people at the games increase from 2005 to 2012
What is Percentage?percentage, a relative value indicating hundredth parts of any quantity.
Given,
The average number of people who attended football games at a stadium in 2005 is 8000.
The average number of people who attended football games at a stadium in 2012 is 12500.
The difference from average number of people from 2005 to 2012
12500-8000
Twelve thousand five hundred minus eight thousand
4500
To find the percentage of increase we need to divide change in number by original number
4500/8000
0.561
Now multiply with 100 because it is a hundredth part.
0.561×100=56.1
Hence 56.1% is the average number of people at the games increase from 2005 to 2012
To learn more on Percentage click:
https://brainly.com/question/28269290
#SPJ2
A prime polynomial cannot be written as a product of a lower-degree polynomials. Which is a prime ?
HELPPPPP

Answers
Answer:
its C
Step-by-step explanation:
two swimmers swam lobstering practice together the swim 175 laps swmmier b swam 25 more than twice as many as swimmer a how many laps did swimmer a swim
Answers
Answer:
swimmer b swims 100 yards. approximately how many more feet did swimmer a swim than swimmer b? 2.
Step-by-step explanation:
help MATH GEOMETRY WILL GIVE BRAINLIEST TO FIRST ANSWER

Answers
15(x+3) = 2x(12)
15x+45 = 24x
45 = 9x
x = 5
PSLS ANSWER !!! <<<<<< The quadrilateral in Quadrant II is the image of the quadrilateral in Quadrant IV after a counterclockwise rotation about the origin.
What is the angle of rotation?
A. 90°
B. 180°
C. 270°
D. 360°

Answers
Answer:
a . 90⁰
hope it will help you
Please help me with this question!


Answers
The two swimming pools will have same amount of water using this equation, where x represents the time in minutes
3300 - 24x = 3696 - 35x
How to find the equation when the two pools will have same amount of waterinformation given in the question is as follows
the first pool had 3300 liters of water and drains at a rate of 24 liters per minute
the second pool had 3696 liters of water and drains at a rate of 35 liters per minute.
The given information implies that
every minute in x minutes 24x liters of water is drained from the first tank.
3300 - 24x
Similarly, in the second tank in x minutes 35x liters of water in drained from the second tank
3696 - 35x
The tanks will have equal volume of water when the two equations are equal
3300 - 24x = 3696 - 35x
Learn more about rate of draining water at:
https://brainly.com/question/28740063
#SPJ1
Someone help me pls thanks :)

Answers
Answer:
I think you need to add them.
Answer:
0.24
Step-by-step explanation:
Miles he drives: x
55.96+0.12x=49.96+0.16x
0.04x=6
x=0.24mi
a random variable x has the following probability distribution. x f(x) 0 0.27 1 0.35 2 0.05 3 0.25 4 0.08 (a) determine the expected value of x. (b) determine the variance.
Answers
The probability distribution of random variable x is
a) 1.78 is the anticipated value of x;
b) The variance of x is 0.6484.
(a) The expected value of x can be found using the formula:
\(E(x) = Σ[x * f(x)]\)
where x's potential values are all added up.
Using the given probability distribution, we have:
\(E(x) = (0 * 0.27) + (1 * 0.35) + (2 * 0.05) + (3 * 0.25) + (4 * 0.08)\)
\(E(x) = 1.78\)
As a result, 1.78 is the expected value of x.
(b) The variance of x can be found using the formula:
\(Var(x) = E(x^2) - [E(x)]^2\)
where E(x) represents the anticipated value of x and E(x2) represents the expected value of x2.
To find E(x^2), we can use the formula:
\(E(x^2) = Σ[x^2 * f(x)]\)
Using the given probability distribution, we have:
\(E(x^2) = (0^2 * 0.27) + (1^2 * 0.35) + (2^2 * 0.05) + (3^2 * 0.25) + (4^2 * 0.08)\)
\(E(x^2) = 3.33\)
Consequently, the variation of x is:
\(Var(x) = E(x^2) - [E(x)]^2\)
\(var(x) = 3.33 - (1.78)^2\)
\(var(x) = 0.6484\) (rounded to four decimal places)
x's variance is 0.6484
As a result, x's variance is 0.6484.
1.78 is the anticipated value of x
To learn more about random variable visit
https://brainly.com/question/17238189
#SPJ4
what is the approximation for the value of cos(12) obtained by using the fourth-degree taylor polynomial for cosx about x
Answers
The approximation for the value of cos(12) using the fourth-degree Taylor polynomial is approximately 505.
We have,
To approximate the value of cos(12) using the fourth-degree Taylor polynomial for cos(x) about x = 0, we can use the formula:
cos(x) ≈ \(1 - (x^2 / 2) + (x^4 / 24)\)
Substituting x = 12 into the formula, we have:
cos(12) ≈ \(1 - (12^2 / 2) + (12^4 / 24)\)
≈ 1 - 72 + 576
≈ 505
Therefore,
The approximation for the value of cos(12) using the fourth-degree Taylor polynomial is approximately 505.
Learn more about polynomials here:
https://brainly.com/question/2284746
#SPJ12
A group of 8 friends went to lunch and spent a total of $76, which included the food bill and a tip of $16. They decided to split the bill and tip evenly among themselves. Which equations and solutions describe the situation? Select two options. The equation StartFraction 1 over 8 EndFraction (x + 16) = StartFraction 76 over 8 EndFraction represents the situation, where x is the food bill. The equation StartFraction 1 over 8 EndFraction (x + 16) = 76 represents the situation, where x is the food bill. The solution x = 60 represents the total food bill. The solution x = 60 represents each friend’s share of the food bill and tip. The equation 8 (x + 16) = 76 represents the situation, where x is the food bill.
Answers
The correct options are:
The equation StartFraction 1 over 8 EndFraction (x + 16) = StartFraction 76 over 8 EndFraction represents the situation, where x is the food bill.
The solution x = 60 represents the total food bill.
What is the equivalent expression?
Equivalent expressions are expressions that work the same even though they look different. If two algebraic expressions are equivalent, then the two expressions have the same value when we plug in the same value for the variable.
Since there are 8 friends and they decided to split the bill and tip evenly among themselves, each friend pays an equal share of the total bill, which is the food bill plus the tip. Let x be the food bill.
Then the total bill is x + 16 (the food bill plus the tip), and each friend's share is StartFraction 1 over 8 EndFraction (x + 16).
So, we have the equation StartFraction 1 over 8 EndFraction (x + 16) = StartFraction 76 over 8 EndFraction, which represents the situation where the total bill is $76 and there are 8 friends. Solving for x, we get:
StartFraction 1 over 8 EndFraction (x + 16) = StartFraction 76 over 8 EndFraction
x + 16 = 76
x = 60
Therefore, the total food bill is $60, which is the solution to the equation.
Each friend's share of the food bill and tip is StartFraction 1 over 8 EndFraction (x + 16) = StartFraction 1 over 8 EndFraction (60 + 16) = $9.
The equation 8(x + 16) = 76 is not correct, as it assumes that the total bill is divided equally among 8 people without taking into account the food bill and the tip separately.
hence, The correct options are:
The equation StartFraction 1 over 8 EndFraction (x + 16) = StartFraction 76 over 8 EndFraction represents the situation, where x is the food bill.
The solution x = 60 represents the total food bill.
To learn more about the equivalent expression visit:
https://brainly.com/question/2972832
#SPJ1
What is a counterexample for the conjecture? if the perimeter of a rectangle is 40 units, the area must be at least 1 square unit.
Answers
The counterexample for the conjecture If the perimeter of a rectangle is 40 units, the area must be at least 1 square unit is: A rectangle with length 19.99 units and width 0.01 unit has a perimeter of 40 units and an area of 0.1999 square unit.
What is counterexample?
The term counterexample refers to an instance or example that makes the statement false. This is used in logic to check if a statement is true or not. Counter example tend to counter the statement being discussed with valid points.
The question wants to show the relationship that may exist between perimeter and area of a rectangle.
The counterexample provided the dimensions that gave the perimeter which is 40 but failed to give area of 1 square unit
Learn more about counterexample at:
brainly.com/question/24881803
#SPJ4
A random sample of 10 observations is selected from a normal population. The sample mean was 11 and the sample standard deviation 3.2. Using the 0.1 significance level:
Answers
The sample mean is significantly different from 10 at a 0.1 significance level.
The null hypothesis is a statement about the population parameter that we are testing, and the alternative hypothesis is the complement of the null hypothesis. The significance level is the probability of rejecting the null hypothesis when it is true.
In this case, we can use the following null and alternative hypotheses:
Null hypothesis: The population mean is equal to 10.
Alternative hypothesis: The population mean is not equal to 10.
We will use a two-tailed test because the alternative hypothesis is not directional.
We can use the t-test to test the null hypothesis. The t-test statistic is calculated as follows:
t = (sample mean - hypothesized mean) / (sample standard deviation / sqrt(sample size))
In this case:
\(t = (11 - 10) / (3.2 / \sqrt{10} ) = 1.58\)
We need to find the critical value of t at the 0.1 significance level with 9 degrees of freedom (10 - 1 = 9). We can use a t-table or a statistical software to find this value. The critical value is ±1.833.
Since the calculated t-value of 1.58 is not greater than the critical value of ±1.833, we cannot reject the null hypothesis. We do not have sufficient evidence to conclude that the population mean is different from 10 at the 0.1 significance level.
for such more question on sample mean
https://brainly.com/question/22920224
#SPJ11
7) You may leave this answer
as a power.
[(3²)²]³
Answers
[(3²)²]³ = (3^4)^3 = 3^(4*3) = 3^12
To simplify [(3²)²]³, we can first simplify the expression inside the parentheses. 3² equals 9, so (3²)² equals 81.
Substituting this value, we get [(81)]³. To simplify this, we can apply the power of a power rule which states that when you raise a power to a power, you multiply the exponents.
So, [(81)]³ is equivalent to 81³. Applying the exponent rule, we get 531,441 as the final answer. Therefore, [(3²)²]³ can be simplified as 531,441.
Learn more about :
parentheses : brainly.com/question/972166
#SPJ11
(2.3x10^4)x(1.5x10^-2
Answers
here's the solution luv

Answer:
3.45x10^2
Step-by-step explanation:
Thankyou
Evaluate each expression below if m = 32 and n = 150
25) 2N - 200
26) m (-12)
Answers
As per the question we have ─
m = 32
n = 150
We need to evaluate each expression given below ─
25) 2n - 200
Putting the value of n = 150
= 2(150) - 200
= 300 - 200
= 10026) m (-12)
putting the value for m = 32
= 32(-12)
= -384Answer:
25) 100
26) -384
Step-by-step explanation:
25) 2 * 150 -200 = 100
26) 32 (-12) = -384
Cofactors and BDDs Consider a 5-variable function f(a,b,c,d,e)defined by a minimal sum-of-products (SOP) expression as follows: f=a′bce+ab′c′e+cde′+a′bc+bce′+ac′d+a′b′c′d′e′ (a) [6 points] Derive the following 6 cofactors of f:fa,fa′,fa′b′,fa′b,fab′,fab. Give your answers in the form of minimal SOP expressions. (b) [10 points ] Construct a neat ROBDD for f assuming top-to-bottom variable order a,b,c,d,e. Label with fx the six nodes of your ROBDD that correspond to your answer for Part (a). (c) [4 points] Now consider other possible orders of the five variables. Without deriving another ROBDD, propose the first variable in a new order that is most likely to yield a smaller ROBDD. Give a brief reason for your answer
Answers
Co-factors:Co-factors represent functions that result when some variables are fixed. The function can be divided into various co-factors based on the variables involved. In general, we can say that co-factors are the functions left when one or more variables are held constant.
Consider the following minimal sum-of-products (SOP) expression of a 5-variable function:f = a′bce + ab′c′e + cde′ + a′bc + bce′ + ac′d + a′b′c′d′e′. We need to derive six co-factors of the given function. They are: f_a, f_a', f_a'b', f_a'b, f_ab', and f_ab.1. f_a: We can take f(a=0) to find f_a = bce + b′c′e + cde′ + bc′d + b′c′d′e′2. f_a': We can take f(a=1) to find f_a' = bce + b′c′e + cde′ + bc + b′c′d′e′3. f_a'b': We can take f(a=b'=0) to find f_a'b' = ce + c′e′ + de′4. f_a'b: We can take f(a=0, b=1) to find f_a'b = ce + c′e′ + cde′ + c′d′e′5. f_ab': We can take f(a=1, b=0) to find f_ab' = ce + c′e′ + b′c′d′e′ + bc′d′e′6. f_ab: We can take f(a=b=1) to find f_ab = ce + c′e′ + b′c′d′e′ + bc′d′e′ROBDD:ROBDD stands for Reduced Ordered Binary Decision Diagram. It is a directed acyclic graph that represents a Boolean function. The nodes of the ROBDD correspond to the variables of the function, and the edges represent the assignments of 0 or 1 to the variables. The ROBDD is constructed in a top-down order with variables ordered in a given way. In this case, we are assuming top-to-bottom variable order a,b,c,d,e.
The ROBDD for the given function is shown below:The six nodes of the ROBDD correspond to the six co-factors that we derived in part (a). The fx labels are given to show which node corresponds to which co-factor.Changing variable order:If we change the variable order, we might get a smaller ROBDD. This is because the variable ordering affects the structure of the ROBDD. The optimal variable order depends on the function being represented. Without deriving another ROBDD, we can propose the first variable in a new order that is most likely to yield a smaller ROBDD.
We can consider the variable that has the highest degree in the function. In this case, variable c has the highest degree, so we can propose c as the first variable in a new order that is most likely to yield a smaller ROBDD. This is because fixing the value of a variable with a high degree tends to simplify the function. However, the optimal variable order can only be determined by constructing the ROBDD.
To know more about Co-factors visit
https://brainly.com/question/13719777
#SPJ11
order from least to greatest
-2 -2 1/2 -3 -3.5 2.5
Answers
According to the given information in the question order from least to greatest -3.5, -3, -2, -2 1/2, 2.5.
More negative number becomes more small i.e. -3.5 will be smallest in the given question.
To know more about order visit:
https://brainly.com/question/8936035
#SPJ1
AB =? Round your answer to the nearest hundredth.

Answers
Answer:
? = 4.41
Step-by-step explanation:
Since this is a right triangle, we can use trig functions
cos A = adj / hyp
cos 25 = 4/?
? = 4/ cos 25
? =4.413511676
To the nearest hundredth
? = 4.41
What is the solution to the system of equations below?
(Hint: Solve using substitution!)
−5x−y=5
x=7y−1
(
Answers
Answer:
x = -1, y = 0 or (-1, 0)Step-by-step explanation:
We have two equations :
-5x - y = 5x = 7y - 1Take the value of x in Equation 2 and substitute in Equation 1.
-5(7y - 1) - y = 5-35y + 5 - y = 5-36y = 0y = 0Now, take the value of y and substitute in Equation 2.
x = 7(0) - 1x = -1Solution
x = -1, y = 0 or (-1, 0)Answer:
The lines intersect at the point (-1, 0)
Step-by-step explanation:
−5( )−y=5
-5(7y-1) - y = 5 substitute the x=7y-1 into first equation
-35y + 5 - y =5 multiply -5
-36y + 5 = 5 combine like terms
-36y = 0 subtract 5
y=0 divide by -36
x=7(0)-1 substitute 0 for y in x=7( )-1
=-1 simplify
The lines intersect at the point (-1, 0)
X
X
60°
60°
X=[ ? 1°
Enter

Answers
x+x+60+60=180
2x=60
X=30
Explanation: a entire triangle has a total of 180 degrees, I’m going to subtract 90 and 60 from 180 and that gives me the remaining amount(side) 30 which is the answer
Please help and hurry 15 points
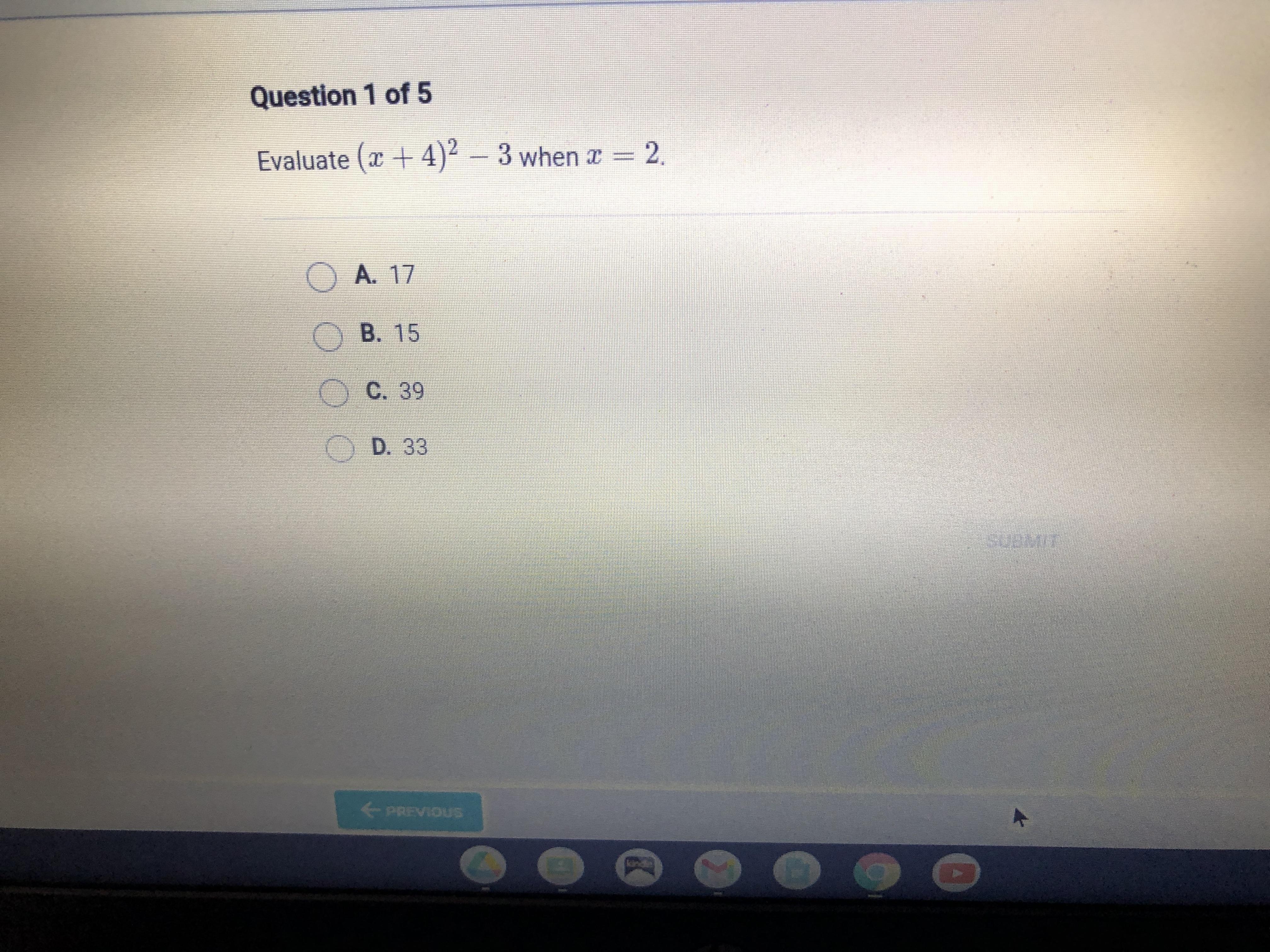
Answers
So substitute the x for 2
(2+4)^2-3
Pemdas
6^2
36-3
33
Answer:
23
Step-by-step explanation:
(x+4) ²-3 (Question)
x²+4x+16-3
x²+4x+13
(2)²+4(2)+13 (since x=2)
4+6+13
23
three machines, a, b, c produce a large number of identical products. 60% of the products come from machine a, 30% from b and 10% from c. historical records indicate that 10% of the parts produced by machine a are defective, compared with 30% for machine b and 40% for machine c. what is the probability that a randomly chosen part is defective?
Answers
The probability that a randomly chosen part is defective is 0.16, or 16%.
The probability that a randomly chosen part is defective, we need to use the law of total probability.
Let \($D$\) be the event that a part is defective and let \($M_i$\) be the event that the part came from machine \($i$\), for \($i = A, B, C$\).
Then we have:
\($P(D) = P(D|M_A)P(M_A) + P(D|M_B)P(M_B) + P(D|M_C)P(M_C)$\)
60% of the products come from machine A, 30% from machine B, and 10% from machine C.
Therefore:
\($P(M_A) = 0.6$\)
\($P(M_B) = 0.3$\)
\($P(M_C) = 0.1$\)
The probability of a part being defective is 10% if it comes from machine A, 30% if it comes from machine B, and 40% if it comes from machine C.
Therefore:
\($P(D|M_A) = 0.1$\)
\($P(D|M_B) = 0.3$\)
\($P(D|M_C) = 0.4$\)
Substituting these values into the law of total probability, we get:
\($P(D) = 0.1 \cdot 0.6 + 0.3 \cdot 0.3 + 0.4 \cdot 0.1 = 0.16$\)
For similar questions on randomly
https://brainly.com/question/24140969
#SPJ11
A spinner is divided into 8 equal sections: What is the theoretical probability of spinning and landing on 2, 7, or 5?
Answers
Answer:
3/8 or
2.67 or
2 67/100
Step-by-step explanation:
2.671×100100=267100
8 divide by 3. Take that and convert to fraction or decimal either or.
