what why did you say you had $80.50 and you add that up
Answers
Answer:
im not sure i understand the question
Step-by-step explanation:
80.50 plus........plus what?
i am confusion
Related Questions
Multiple choice: Select the best answer for Exercises 49 to 52. Most people can roll their tongues, but many can’t. The ability to roll the tongue is genetically determined. Suppose we are interested in determining what proportion of students can roll their tongues. We test a simple random sample of 400 students and find that 317 can roll their tongues. The margin of error for a 95% confidence interval for the true proportion of tongue rollers among students is closest to (a) 0.008. (b) 0.02. (c) 0.03. (d) 0.04. (e) 0.208.
Answers
The margin of error for a 95% confidence interval for the true proportion of tongue rollers among students is closest to (d) 0.04
The margin of error is a statistic that describes how much random sampling error there is in survey results.
Given in question,
n = 400
p = 317/400
= 0.7925
Confidence Level = 95%
= 0.95
Formula for margin error, E = \(z\sqrt{\frac{p(1-p)}{n} }\)
Confidence level corresponding to 95 % confidence interval, z = 1.96
Therefore,
Margin Error, E = \(1.96\sqrt{\frac{0.7925(1-0.7625)}{400} }\)
= 0.0397
≈ 0.04
Hence, The margin of error for a 95% confidence interval for the true proportion of tongue rollers among students is 0.0397 which is closest to 0.04.
To learn more about margin of error here:
https://brainly.com/question/10501147
#SPJ4
derivate (cos(3x^2). (5x^3 -1)^1/3 +sin 4x^3)^4
\( \: \: \: \: find \: first \: derivative \\ ( cos(3x {}^{2} ) \times ( \sqrt[3]{5x {}^{3} - 1} ) + \sin(4x {}^{3} ) {}^{4} \)
Answers
Answer:
Step-by-step explanation:
\(\frac{d}{dx} [cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)]^4\\\\=4[cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)]^3\; \frac{d}{dx} [cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)] --- eq(1)\)
Lets look at the derivative part:
\(\frac{d}{dx} [cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)] \\\\= \frac{d}{dx}[cos(3x^2) \sqrt[3]{5x^3 -1} ] + \frac{d}{dx}[sin(4x^3)]\\\\=cos(3x^2) \frac{d}{dx}[ \sqrt[3]{5x^3 -1} ] + \sqrt[3]{5x^3 -1}\frac{d}{dx}[ cos(3x^2) ] + cos(4x^3) \frac{d}{dx}[4x^3]\\\\=cos(3x^2) \frac{1}{3} (5x^3 -1)^{\frac{1}{3} -1} \frac{d}{dx}[5x^3 -1] + \sqrt[3]{5x^3 -1} (-sin(3x^2))\frac{d}{dx}[ 3x^2] + cos(4x^3)[(4)(3)x^2]\)
\(=\frac{cos(3x^2) 5(3)x^2}{3(5x^3 - 1)^{\frac{2}{3} }} -\sqrt[3]{5x^3 -1}\; sin(3x^2) (3)(2)x + 12x^2 cos(4x^3)\\\\=\frac{5x^2cos(3x^2) }{(5x^3 - 1)^{\frac{2}{3} }} -6x\sqrt[3]{5x^3 -1}\; sin(3x^2) + 12x^2 cos(4x^3)\)
Substituting in eq(1), we have:
\(\frac{d}{dx} [cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)]^4\\\\=4[cos(3x^2) \sqrt[3]{5x^3 -1} +sin(4x^3)]^3\; [\frac{5x^2cos(3x^2) }{(5x^3 - 1)^{\frac{2}{3} }} -6x\sqrt[3]{5x^3 -1}\; sin(3x^2) + 12x^2 cos(4x^3)]\)
Can u pleaseee answer all parts pleaseeeee <3333
please help meee


Answers
a. In interval notation, Increasing intervals: (12pm, 1pm) U (1pm, 2pm) U (2pm, 3pm). Decreasing intervals: (8am, 9am) U (11am, 12pm). Constant intervals: (9am, 10am) U (10am, 11am)
b. The increase in cost between 12 noon and 3 pm is $2.
c. Yellow Cab has a lower price per 1km than Swift ride at (8am, 9am) (9am, 10am) (2pm 3pm)
How do you express a data set in interval notations?Interval notation is used to represent continuous intervals of numbers or values, like ranges on a number line.
The graph shows that from 8-9am, and 11-12pm, the cost from Swift Ride decreases.
We can represent it as (8am, 9am) U (11am, 12pm).
It increases at these times (12pm, 1pm) U (1pm, 2pm) U (2pm, 3pm).
And stays constant at : (9am, 10am) U (10am, 11am)
Cost increase from 12 to 3pm,We simply deduct the 12pm's cost from 3pm's cost.
So, we have
Cost increase = $3.5 - $1.5
Evaluate the difference
Cost increase = $2
Hence, the cost increase is $2
The time interval where the cost is lowerWhen you plot the points provided for Yellow cab, you'll notice that Yellow Cab has a lower price per 1km than Swift ride at (8am, 9am) (9am, 10am) (2pm 3pm)
Find more exercises on Interval notation;
https://brainly.com/question/17249352
#SPJ1
Boris started on the treadmill after setting timer for 99 minutes. The display says he have finished 43% of his run. How many minutes have gone by. Round to the nearest tenth
Answers
99 minutes * 0.43 = 42.57 minutes
Rounding to the nearest tenth, we can say that approximately 42.6 minutes have gone by.
Select the system of linear inequalities whose solution is graphed. O y < 3x-2, x + 2y > 4 O y ≤ 3x-2, x + 2y 2 4 O y> 3x-2, x + 2y < 4 O y2 3x-2, x + 2y ≤ 4
Answers
Option D is the correct answer.
From the graph, we can conclude that,
1. The two lines are continuous lines and not broken lines. So, the inequality sign should be either ≤ or ≥.
2. The points on the lines of the shaded region are also included in the solution.
The only option that matches with the above conditions is option D. So, option D is the correct answer.
Let us verify it.
Now, let us consider a point that is inside the shaded region and also on any one line.
Let us take (0, 2).
Plug in 0 for x and 2 for y in each of the options and check which inequality holds true.
Considering the inequalities,
y ≥ 3x - 2
x + 2y ≤ 4
Solving we get,
2 ≥ 3(0) - 2
2 ≥ -2
x + 2y ≤ 4
0 + 2(2) ≤ 4
4 ≤ 4
Here, both inequalities are correct.
So, option D is the correct answer.
Learn more about inequality click
https://brainly.com/question/20383699
#SPJ1
The complete question is =
Which system of linear inequalities is graphed?
A. y < 3x-2
x + 2y ≥ 4
B. y < 3x - 2
x + 2y > 4
C. y > 3x - 2
x + 2y < 4
D. y ≥ 3x - 2
x + 2y ≤ 4

H. Salaries of Ravi and Sumit are in the ratio 2 : 3. If the salary of each is increased by Rs. 4000, the new ratio becomes 40 : 57. What is Sumit's salary?
Answers
Answer:
so here is the answer hope it helps

Distance - rate and time formula
Answers
PLSSS HELP ME 14 POINTS

Answers
The transformation of f(x) to g(x) is :
Vertically compressed by a factor of 9Shifted down by 2 Describing the transformation of the functionsFrom the question, we have the following parameters that can be used in our computation:
The functions f(x) and g(x)
Where, we have
f(x) = x
g(x) = 1/9x - 2
The graph of the functions f(x) and g(x) are added as an attachment
And we have the transformations to be:
Vertically compressed by a factor of 9Shifted down by 2Read more about transformation at
brainly.com/question/27224272
#SPJ1

Find length MP
Please help;)

Answers
Answer:
MP = 19
Step-by-step explanation:
17+3y=5y+9
or, 17-9 = 5y-3y
or, 8=2y
so, y = 2
Now,
MP = 5y+9
or, MP = 5×2+9
or, MP = 10+9
so, MP = 19
An earthquake with a rating of 7.9 is
known to be a great earthquake that can
cause damage that extends several
hundred kilometers.
R = log x
R = rating of the earthquake's size on the
Richter scale
x = ratio of earthquake intensity to a
minimum level of intensity
1) Substitute known values into the
equation.
2) Raise each side of the equation as the
power of the base of the log.
3) Simplify using the property.
What is the value of x when the Richter
scale rating is 7.9? Round your answer
to the nearest hundredth.
Enter the correct answer.
DONE

Answers
The value of x when the Richter scale rating is 7.9 is approximately 79432.82
How to find the valueTo find the value of x when the Richter scale rating is 7.9, we can follow the steps provided:
Substitute known values into the equation.
R = log(x)
R = 7.9
Raise each side of the equation as the power of the base of the log.
\(10^R = 10^(^l^o^g^(^x^)^)\)
Simplify using the property.
\(10^R = x\)
Now we can substitute the value of R (7.9) into the equation:
\(10^(^7^.^9^) = 79432.82\)
Therefore, the value of x when the Richter scale rating is 7.9 is approximately 79432.82 (rounded to the nearest hundredth
Read more on richter scale here:https://brainly.com/question/24037139
#SPJ1
Differentiate the function with respect to x. Shot steps

Answers
Differentition of \(y=log_{2}x^{3}.(5x^{4}+2)\) is \(y'=log_{2}x^{3}(20x^{3} )+(5x^{4}+2)\frac{1}{x}\)
What is Differential equation?A differential equation is an equation that contains one or more functions with its derivatives.
Given,
\(y=log_{2}x^{3}.(5x^{4}+2)\)
We have to differentiate with respect to x.
y'=xy'+yx'
\(x=log_{2}x^{3}\)
\(y=5x^{4}+2\)
\(y'=log_{2}x^{3}(20x^{3} )+(5x^{4}+2)\frac{1}{x^{3}} .3x^{2}\)
\(y'=log_{2}x^{3}(20x^{3} )+(5x^{4}+2)\frac{1}{x}\)
Hence, differentiation of \(y=log_{2}x^{3}.(5x^{4}+2)\) is \(y'=log_{2}x^{3}(20x^{3} )+(5x^{4}+2)\frac{1}{x}\)
To learn more on Differentiation click:
https://brainly.com/question/24898810
#SPJ1
parallel to 3y – 2x = – 2, passes through (3, –3)
Answers
y = 2/3x -6
Conditions for Lines to be parallel
If two straight lines are cut by a transversal, the pair of alternate angles are equal, then two straight lines are parallel to each other. the pair of interior angles on the same side of traversals is supplementary, then the two straight lines are parallel.
Given line
3y – 2x = – 2
passes through (3, –3)
The slope-intercept form is
y =mx+b,
where m is the slope and
b is the y-intercept.
y = mx+b
Divide each term in
3y – 2x = – 2 by -2 and simplify.
-3/2y +x =1
Reorder terms.
y = -(2/3)(x+1)
Using the slope-intercept form, the slope is
2/3.m=2/3
To find an equation that is parallel, the slopes must be equal. Find the parallel line using the point-slope formula.
Use the slope
2/3 and a given point (3, –3)
to substitute for
x1 and y1
in the point-slope form
y−y1=m(x−x1)
which is derived from the slope equation
m=(y2−y1)x2−x1.
y−(-3)=2/3⋅(x−(3))
Simplify the equation and keep it in point-slope form.
y+4=2/3⋅(x-3)
y = 2/3x -6
To learn more about Parallel lines
visit - https://brainly.in/question/473305
#SPJ9
Think About the Process Van purchased a DVD player on sale. The original selling price was $179.30. The sale price was
$157.17. What is the first step in finding the percent markdown? Find the percent markdown.
What is the first step in finding the percent markdown?
OA. Find the cost.
OB. Find the greatest markdown possible.
C. Find the markdown.
The percent markdown was%. (Round to the nearest whole number as needed.)
Answers
Answer:19.26%
Step-by-step explanation: yeah
Answer:
19%
Step-by-step explanation:
There are only 5 steps here they are:
1. Divide 144.77 by 179.30
2. You get the answer 0.80741773...
3. You round it to 0.81.
4. You turn it into a percent by moving the dot(decimal) to the right four times.
5. And then you subtract it from 100 and you get 19% for the discount.
so therefore the answer is 19%
here some other answer that is just like this one:
https://brainly.com/question/1030112
The machinery in a cereal plant fills 350 g boxes of cereal. The specifications for the machinery permit for a certain amount of fill tolerance. It is found that the weights of filled cereal boxes are normally distributed with a mean of 350 g and a standard deviation of 4 g. What is the probability that a box of cereal is under filled by 5 g or more?
Answers
There is approximately an 89.44% probability that a box of cereal is underfilled by 5 g or more.
To find the probability that a box of cereal is underfilled by 5 g or more, we need to calculate the probability of obtaining a weight measurement below 345 g.
First, we can standardize the problem by using the z-score formula:
z = (x - μ) / σ
Where:
x = the weight value we want to find the probability for (345 g in this case)
μ = the mean weight (350 g)
σ = the standard deviation (4 g)
Substituting the values into the formula:
z = (345 - 350) / 4 = -1.25
Next, we can find the probability associated with this z-score using a standard normal distribution table or a statistical calculator.
The probability of obtaining a z-score less than -1.25 is approximately 0.1056.
However, we are interested in the probability of underfilling by 5 g or more, which means we need to find the complement of this probability.
The probability of underfilling by 5 g or more is 1 - 0.1056 = 0.8944, or approximately 89.44%.
Therefore, there is approximately an 89.44% probability that a box of cereal is underfilled by 5 g or more.
For more questions on probability
https://brainly.com/question/251701
#SPJ8
The digits of a two-digit number sum to 8. When the digits are reversed, the resulting number is 18 less than the original number. What is the original number?
26
35
53
62
Answers
Answer:
original number = 53
Step-by-step explanation:
In two digits number:
Let the tens place digit be x and units place digit be y.
So,
Original number = 10x + y
Number obtained after reversing the digits = 10y + x
According to the first condition:
x + y = 8.... (1)
According to the second condition:
10y + x = 10x + y - 18
10y + x - 10x - y = - 18
9y - 9x = - 18
-9(x - y) = - 18
x - y = - 18/(-9)
x - y = 2.......(2)
Adding equations (1) & (2), we find
x + y + x - y = 8 + 2
2x = 10
x = 10/2
x = 5
Plug x = 5 in equation (1), we find:
5 + y = 8
y = 8 - 5
y = 3
10x + y = 10*5 +3 = 50 + 3 = 53
Hence, original number = 53
Ricardo ran four miles in 31 minutes. It took him 6.25 minutes to run the first mile. Ricardo ran the remaining miles at a slow and steady speed. How long did it take him to run each of the last three miles?
Answers
Answer:
8.25 minutes
Step-by-step explanation:
31 minutes-6.25 minutes=24.75 remaining miutes between the last 3 miles so then you take 24.75 minutes÷ 3 miles remaining= 8.25 minutes each last 3 miles
What's the lcm for 18, 27, 12? I got 648. Am not sure if it is correct. Can you please explain if it is correct or not?
Answers
Answer:
Step-by-step explanation:
Put these numbers into their prime factors.
18: 2 * 3 * 3
27: 3 * 3 * 3
12: 2 * 2 * 3
The LCM must have
two 2s
Three 3s
That's it
2*2 * 3 * 3 * 3
LCM = 108
648 might be a multiple of the three, but it's not the smallest one.
108 = 27 * 4
108 = 18 * 6
108 = 12 * 9
Bo took a walk. From his house he went 2 blocks west, 7 blocks north, 3 blocks west, 4 blocks south, and 5 blocks east. How far was he from his home?
Answers
Lines that appear to be tangent are tangent. O is the center of each circle.
What is the value of x? Show all work to receive full credit.

Answers
Note that in the prompt above, the value of x is given as: 16°
To answer the issue, we will first name all of the points supplied to us on the isosceles triangle, then identify O, and last discover the value of x. See the attached image.
What is an isosceles triangle?As a result, an isosceles triangle has two equal sides and two equal angles. The term is derived from the Greek words iso (same) and skelos (skull) (leg). An equilateral triangle has all of its sides equal, whereas a scalene triangle has none of its sides equal.
In ΔAOB
OA = OB = R, the radius of the circle O,
therefore, the ΔAOB is an isosceles triangle, with OA, OB as the congruent sides and AB as the base of the triangle.
Thus, ∠OAB = ∠OBA = 53°
Sum of all the angles of a triangle = 180°
∠O + ∠AOB + ∠OBA = 180°
We know ∠AOB = ∠OBA, therefore,
∠O + 2(∠AOB) = 180°
∠O + 2(53°) = 180°
∠O = 180 - 106
∠O = 74°
In ΔOBC,
BC is the tangent to the circle O, therefore,
∠OBC = 90°
Sum of all the angles of a triangle = 180°
∠O + ∠OBC + ∠OCB = 180°
74° + 90° + ∠OCB = 180°
∠OCB = 180° - 74° - 90°
∠OCB = 16°
Hence, the value of x is 16°.
Learn more about the Isosceles triangle:
https://brainly.com/question/2456591
#SPJ1

Andre has $39 and owes Billy $72 for gas and
groceries. How much money does Andre have?
Answers
Answer:
$-33
Step-by-step explanation:
Andre still owes Billy money. If Andre paid Billy the 39 dollars he has, he would still owe Billy $33, which puts him $33 in the hole.
helppp please, cause I really need it tomorrow

Answers
Answer:
who asked
Step-by-step explanation:
Select the point that is a solution to the system of inequalities.
A- (2,6)
B- (0,8)
C-(-2,-4)
D-(4,2)
HELP PLEASE!!!!!

Answers
Explanation:
y < x^2 + 6
6 < 2^2 + 6
6 < 4 + 6
6 < 10 IT WORKS
y > x^2 - 4
6 > 2^2 - 4
6 > 4 - 4
6 > 0 IT WORKS
(Could I also get brainliest please?)
Answer:
its A
Step-by-step explanation:
Algebra Question
Question attached in photo

Answers
Answer:
\(1. \: 9tx {}^{2} - 3tx - 2t \\ \\ 2. \: 3tx {}^{2} + 2tx + 2t\)
Step-by-step explanation:
\(1. \: t(9x {}^{2} - 3x - 2) \\ 2. \: 9tx {}^{2} - 3tx - 2t \\ \\ \\ 1. \: t \times 3x {}^{2} + t \times 2x + t \times 2 \\ 2. \: 3tx {}^{2} + t \times 2x + t \times 2 \\ 3. \: 3tx {}^{2} + 2tx + t \times 2 \\ 4. \: 3tx {}^{2} + 2tx + 2t\)
a model of a car is 4 inches long. if the actual car is 10 feet long, find the scale of the model. a. 4 in
Answers
Scale of the model is found to be 1 : 30 using the ratio method.
A model of a car is 4 inches long.
The actual car is 10 feet long.
4 in. = 10 ft. ( since given )
Divide both sides by 4, we get
∴ 1 in. = 2.5 ft.
We use the ratio here to compare the lengths of the actual car and its model.
A ratio scale is a quantitative measurement scale that is used to compare numbers.
The model is 4 inches long while the actual car is 10 feet long.
One foot is equal to 12 inches. Therefore the car in terms of inches is:
10 feet × 12 inches = 120 inches
The ratio scale is the length of the model of the car : length of the actual car
= 4 : 120
= 1 : 30
Therefore the scale of the model is 1: 30.
Learn more about the ratio scale here :
https://brainly.com/question/13770371
#SPJ4
If f(x) = 6x - 9 and g(x) = x + 6,
which statement is true?
Click on the correct answer.
6 is not in the domain of fog.
6 is in the domain of fºg.
Answers
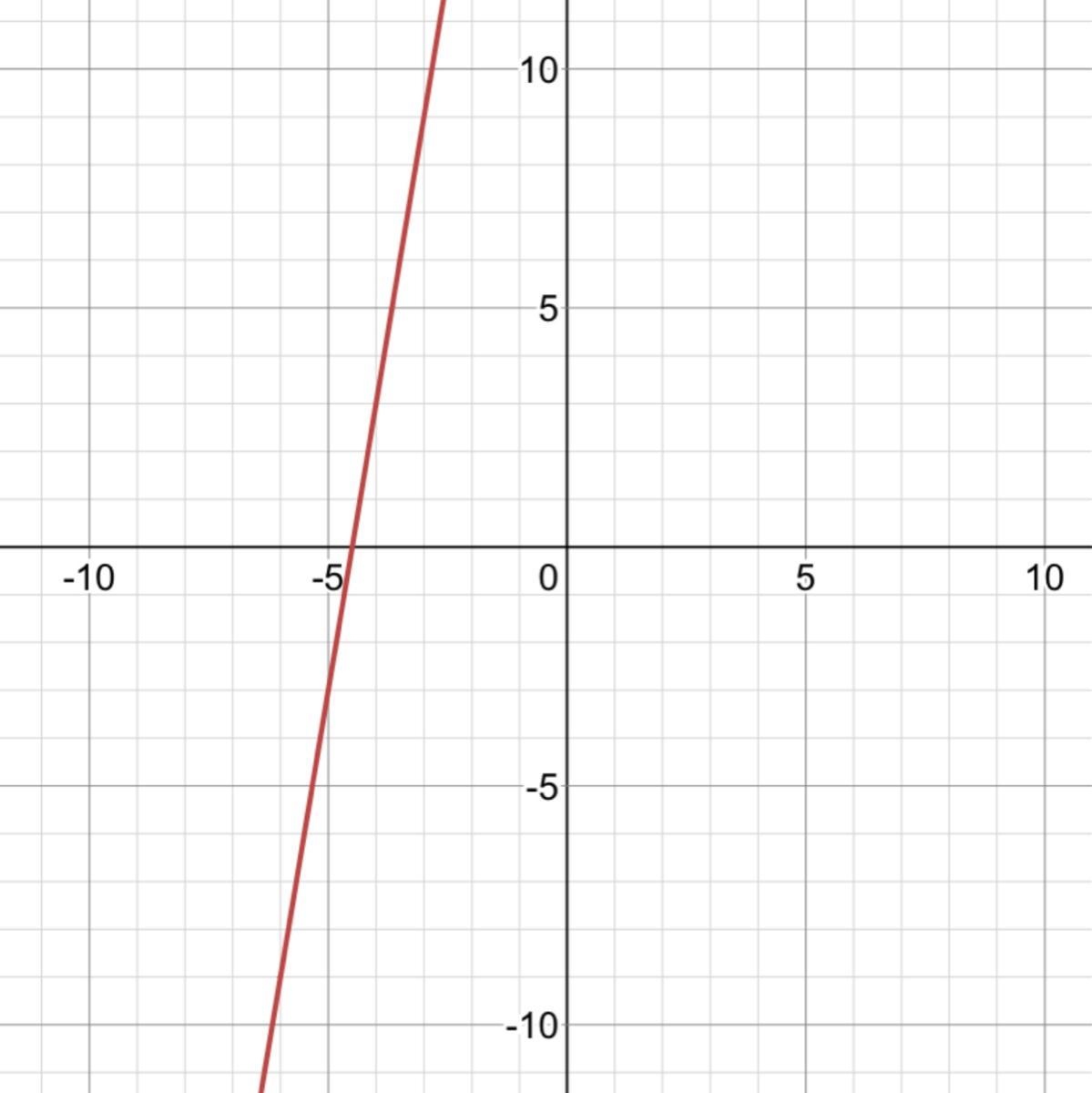
6 is in the domain of f(g).
This is because the domain of the composition function is -infinite to +infinite therefore 6 is a real positive number making it part of the domain as shown in the graph below :)
(EXTREMELY HARD 1000000000 POINTS)
Use the two triangles below to complete all parts to this question. Explain with as many details as possible.
You can score: 0 pt (left blank or completely wrong); 1 pt (correct answer, no explanation); 2 pts (correct answer, minimal details); 3 pts (correct answer, more than 2 details)
State whether the two figures are congruent or similar. Then provide at least two reasons how you know to support your answer. Provide as many details as you can think of.

Answers
Answer:
The triangles are similar, because angles are congruent and corresponding sides have same ratio.=========================
Compare all of the corresponding parts.
Angles∠A ≅ ∠D = 36°∠B ≅ ∠E = 63°∠C ≅ ∠F = 81°All three angles are congruent
SidesAB = 5, DE = 10, DE/AB = 2BC = 2, EF = 4, EF/BC = 2AC = 4, DF = 8, DF/AC = 2Corresponding sides have a ratio of 2.
According to our findings the triangles are similar:
ΔABC ~ ΔDEFAnswer:
ΔABC and ΔDEF are similar triangles as their corresponding angles are the same and their corresponding sides are in proportion.
Step-by-step explanation:
Definitions
Two triangles are said to be congruent if their corresponding angles are the same and their corresponding sides are the same.
Two triangles are said to be similar if their corresponding angles are the same and their corresponding sides are in proportion.
From inspection of the given diagram, the corresponding angles of ΔABC and ΔDEF are the same, but their corresponding sides are in proportion. Therefore, they are similar triangles.
Proof of proportionality:
\(\sf AB = 5, \;\;DE = 10\;\;\implies \dfrac{DE}{AB} = \dfrac{10}{5}=2\)
\(\sf AC = 4, \;\;DF = 8\;\; \implies \dfrac{DF}{AC} = \dfrac{8}{4}=2\)
\(\sf BC = 2, \;\;EF = 4\;\; \implies \dfrac{EF}{BC} = \dfrac{4}{2}=2\)
Therefore, the sides of ΔDEF are twice the length of the sides of ΔABC.
A fair dice is rolled 3 times in a row. The outcomes are shown below.
Calculate the probability of all three events occurring.
Roll Outcome
1st 2
2nd prime
3rd more than 4
Answers
The probability of roll outcome:
1st 2 = 1/6
2nd prime = 1/2, and
3rd more than 4 = 1/3.
What is probabilityProbability is the fraction of the required outcome event divided by the number of possible outcomes of events.
In a fair die, considering the outcomes from the question:
There is only one side with the number 2There are only three prime numbers, 2, 3, and 5There are only two numbers more than 4, which are 5 and 6.probability of the 1st roll to be 2 = 1/6
probability of 2nd roll to be prime = 3/6
probability of 2nd roll to be prime = 1/2
probability of 3rd roll to be more than 4 = 2/6
probability of 3rd roll to be more than 4 = 1/3
Therefore, the fracions 1/6, 1/2, and 1/3 are the probabilities of the 1st, 2nd, and 3rd rolls outcome respectively.
Learn more about probability here: https://brainly.com/question/24830485
#SPJ1
what are 4 different slopes
Answers
Answer:
negative, positive, zero, and undefined
Step-by-step explanation:
The images below show a picture of ricoffy tin container with no dimensions indicated.the container is 2,5 times smaller than what it is in reality. Measure the diameter of the tin in mm and write down the real diameter in mm
Answers
The diameter of the tin in the picture is \(3d/5\) where 'd' is the diameter of the tin in reality.
What is the measurement of the diameter?Determining the diameter of tin:
Since there is no indication of dimensions, represent the diameter with a variable 'd' and find the diameter of the tin according to the given condition in the problem.
Here we have assumed that the diameter of the tin is 'd' in reality and the diameter of the tin picture can be calculated as given below.
Here we have
A ricoffy tin container with no dimensions indicated
Let d and h be the diameter and height of the tin
Given that the container is 2/5 times smaller than d
then the diameter of the tin in the picture \(= d - 2/5(d)\)
\(= [5d - 2d]/5 = 3d/5\)
Therefore, The diameter of the tin in the picture is \(3d/5\) where 'd' is the diameter of the tin in reality.
Learn more about diameter here:
https://brainly.com/question/5501950
#SPJ1
The equation of a circle is:
(x-2)^2 + (y+4)^2 = 25
Part A:
Determine the center and the radius of the circle.
...is this correct?

Answers
The requried center and radius of the given circle are (2, -4) and 5.
The standard equation of a circle is given as,
(x - h)² + (y - k)² = r²
Where, (h, k) is the center of the circles and r is the radius of the circle,
The equation of the given circle is,
(x - 2)² + (y + 4)² = 25
Comparing the above equation with the standard equation we have,
(h, k) = (2, -4)
r² = 5²; r =5
Thus, the requried center and radius of the given circle is (2, -4) and 5.
Learn more about Circle here:
https://brainly.com/question/29288238
#SPJ1