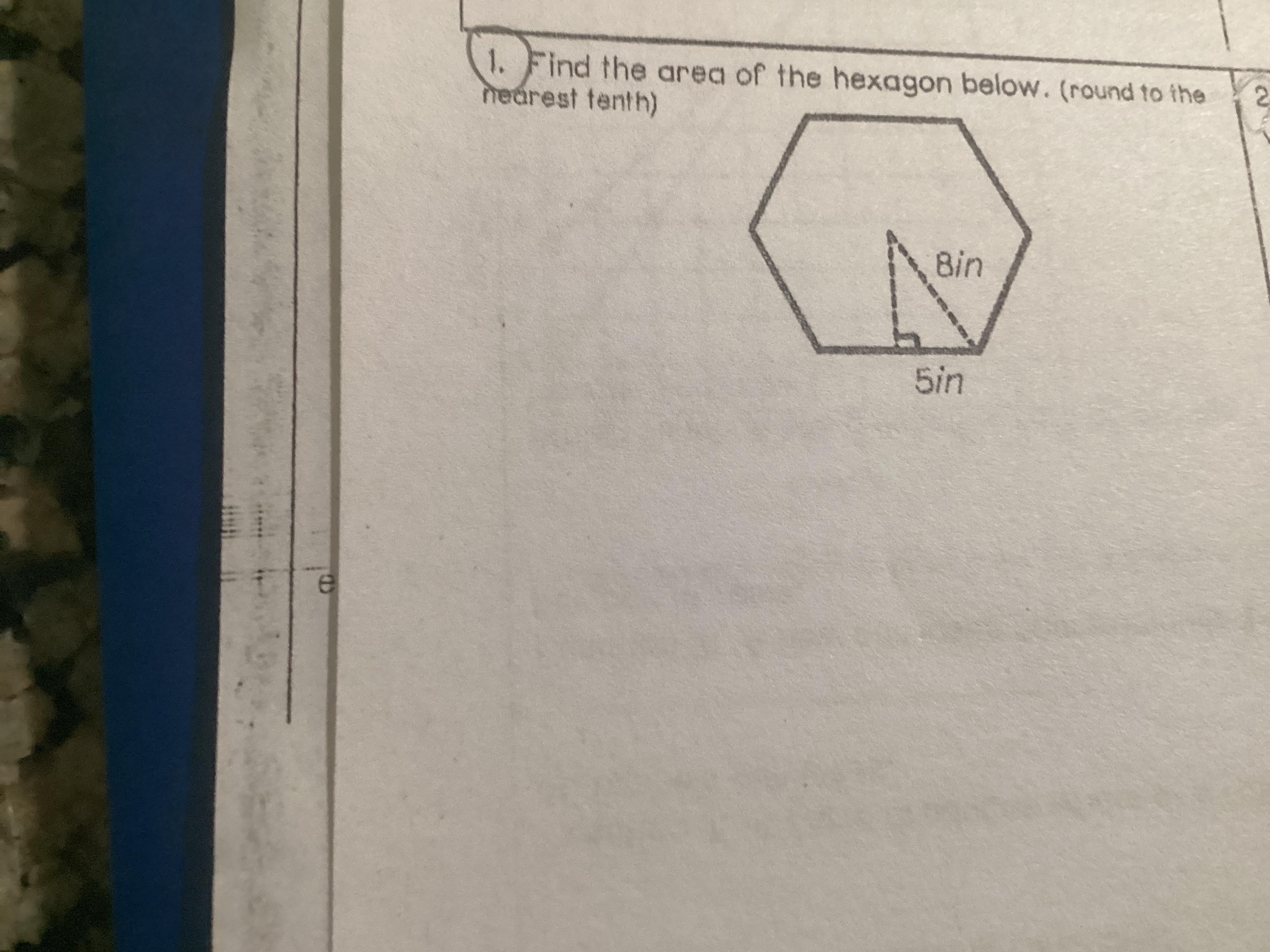
What’s the area of the hexagon rounded to the nearest tenth and how did you find that answer?
Answers
Answer: A ≈ 166.28
Step-by-step explanation:
look at image

Answer: 187.3 in²
Step-by-step explanation:
A= (1/2)aP a is the apothem(center to midpoint of side)
P(perimeter)
P can be found by seeing that 1 of the sides is 10 in. long and multiplying by 6 sides
P=10*6=60
a, apothem, can be found by pythagorean.
c²=a²+b²
8²=a²+5²
a²=39
a=√39=6.24
A = 1/2 (6.24)(60)
=187.3 in²
Related Questions
Please help!
Provide an appropriate response and show your work. Assume that the random variable X is normally distributed, with mean=90 and standard deviation=12. Compute the probability P(57 < X < 105).
Answers
The probability that X is between 57 and 105 is 0.8914.
How to solveGiven:
* X is normally distributed with mean=90 and standard deviation=12
* P(57 < X < 105)
Solution:
* Convert the given values to z-scores:
* z = (X - μ) / σ
* z = (57 - 90) / 12 = -2.50
* z = (105 - 90) / 12 = 1.25
* Use the z-table to find the probability:
* P(Z < -2.50) = 0.0062
* P(Z < 1.25) = 0.8944
* Add the probabilities to find the total probability:
* P(57 < X < 105) = 0.0062 + 0.8944 = 0.8914
Therefore, the probability that X is between 57 and 105 is 0.8914.
Read more about probability here:
https://brainly.com/question/24756209
#SPJ1
The Morris family rented
boat over Labor Day weekend. The boat uses an average of 2 gallons of gas per hour
when it is pulling water skiers and 1 gallon per hour when not pulling water-skiers. The gas for the boat costs $2.25
per gallon How much money is spent on gas per hour when the boat is pulling water-skiers if the Marris family only
water skied for 2 hours?
Answers
The total amount spent on gas is $9.
How much is spent on gas?Multiplication is the mathematical operation that is used to determine the product of two or more numbers. Multiplication is the method that is used to add a number by itself a particular number of times. The sign used to denote multiplication is x. Other mathematical operations are subtraction, division and addition.
In order to determine the total amount spent on gas, multiply the cost of one gallon by the number of hours skied and the amount of galloons used per hour.
The total amount spent on gas = cost of one gallon of gas x number of hours skied x number of gallons used per hour
2 x 3 x $2.25 = $9
To learn more about multiplication, please check: https://brainly.com/question/3385014
#SPJ1
Answer:
Step-by-step explanation:
The total amount spent on gas is $9.How much is spent on gas?Multiplication is the mathematical operation that is used to determine the product of two or more numbers. Multiplication is the method that is used to add a number by itself a particular number of times. The sign used to denote multiplication is x. Other mathematical operations are subtraction, division and addition. In order to determine the total amount spent on gas, multiply the cost of one gallon by the number of hours skied and the amount of galloons used per hour. The total amount spent on gas = cost of one gallon of gas x number of hours skied x number of gallons used per hour 2 x 3 x $2.25 = $9To learn more about multiplication, please check:
How long is the side of a square field if it's perimeter is 1 and 1/2 miles
Answers
Answer:
0.375 miles on each side.
Step-by-step explanation:
Since a square is equal on each side, and has 4 sides, we can take 1.5 miles and divide it by 4:
1.5 divided by 4 = 0.375 miles per side
May I have Brainliest please? My next rank will be the highest one: A GENIUS! Please help me on this journey to become top of the ranks! I would really appreciate it, and it would make my day! Thank you so much, and have a wonderful rest of your day!
Answer:
\(\dfrac{3}{8}\;\;\sf miles\)
Step-by-step explanation:
A square is a quadrilateral (4-sided shape) with sides of equal length.
The perimeter of a two-dimensional shape is the distance all the way around the outside.
Therefore, the perimeter of a square is four times its side length.
Given:
Perimeter of a square is 1 and 1/2 miles."s" is the side length of the square.\(\begin{aligned}\textsf{Perimeter of a square}&=4s\\\\\implies 1\frac{1}{2}&=4s\\\\\dfrac{3}{2}&=4s\\\\s&=\dfrac{3}{2} \div 4\\\\s&=\dfrac{3}{2} \times \dfrac{1}{4}\\\\s&=\dfrac{3 \times 1}{2\times4}\\\\s&=\dfrac{3}{8}\; \sf miles \end{aligned}\)
Therefore, the side length of a square field with a perimeter of 1 and 1/2 miles is 3/8 miles.
Please help due tonight.

Answers
Answer:
I think the answer is C
Step-by-step explanation:
find the value of x and y. SHOW WORK

Answers
Answer:
y = 35
x = 21
Step-by-step explanation:
y+75 = 3y+5
75 - 5 = 3y - y
70 = 2y
y = 70/2
y = 35
3x+7 = 5x-35
7 + 35 = 5x - 3x
42 = 2x
x = 42/2
x = 21
check:
(3x+7) + (y+75) + (5x-35) + (3y+5) = 360
(3*21 + 7) + (35 + 75) + (5*21 - 35) + (3*35 + 5) = 360
(63+7) + (110) + (105-35) + (105+5) = 360
70 + 110 + 70 + 110 = 360
What is the capacitive resistance of a 0.04 microfarad capacitor in a AC circuit that has a frequency of 1,000 hertz?
Answers
Luz, a math major, sees the drawing above as a Venn diagram. Her brother, an art major, sees it as two circles. The difference in perception is an example of…
a. synesthesia.
b. stereotyping.
c. stimulus variables.
d. top-down processing.
e. feature detection.
Answers
Option A, The image above, according to math central Luz, is a Venn diagram. A major in art, her brother, interprets it as two circles. One instance of synesthesia is the discrepancy in perception.
A Venn diagram is a type of visual representation that uses circles to emphasize the relationships among certain items or constrained groups of things. Rings with overlaps have several properties that circles without overlaps do not. Venn diagrams are helpful for visually illustrating the relationship and differences between two concepts.
A Venn diagram uses circles or other overlapping shapes to illustrate the relationships between three or more organizations of things. They usually serve to visually organize items while emphasizing their similarities and differences.
A triple Venn diagram is a helpful visual tool highlighting the similarities and differences between three sets of objects or statistics.
Learn more about the Venn diagram at
https://brainly.com/question/6317465?referrer=searchResults
#SPJ4
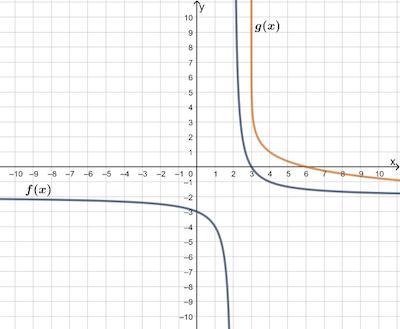
What is the interval in which both f (x) and g(x) are negative?
(–∞, 2) ∪ (2, ∞)
(2, ∞)
(3, ∞)
(6, ∞)
Answers
Based on the graph provided, g(x) is negative only on the interval (6, infty), since that's when the y-values of g(x) are negative (or below the x-axis).
On that interval of (6,infty), f(x) is also below the x-axis, so (6,infty) is your answer.
kendra rides her bike to school each day. it takes her 10 minutes to ride 30 blocks. what unit rate expresses the speed of kendra's bike ride? 2 block
Answers
The unite rate of the kendra's bike ride is found as 3 blocks / min.
Explain the meaning of the term unit rate?An item's unit rate is its price for one of it. This is expressed as a ratio with the number one as the denominator. A particular kind of ratio is a unit rate (or called a single-unit rate). One unit of one quantity will be compared to an unique number of units of another quantity.The given question is-
Total blocks covered = 30.Total time taken = 10 minutesUnit rate = number of blocks/ total time
Unit rate = 30 / 10
Unit rate = 3 blocks / min
Thus, the unit rate of the kendra's bike ride is found as 3 blocks / min.
To know more about the unit rate, here
https://brainly.com/question/4895463
#SPJ4
A bottle of juice costs $1.85, and a pack of 6 bottles of lemonade costs $5.40. If Jimmy
buys 3 bottles of juice and a dozen bottles of lemonade, how much money should he
spend in all?
Answers
Answer:
Step-by-step explanation:
+
1.85
5.40
_____
6. 2 5
21. A 10 ft wide side walk has an effective walkway width of 6.5ft. The peak 15 minutes pedestrian flow is 1200 pedestrians. The plantation adjusted LOS is most nearly. a) LOS B b) LOS C c) LOS D
Answers
The pedestrian flow is the number of pedestrians that pass through a certain area within a specific time frame. In this case, the peak 15-minute pedestrian flow is given as 1200 pedestrians.
To determine the plantation adjusted level of service (LOS), we need to compare the effective walkway width to the pedestrian flow. The effective walkway width is 6.5 ft.
First, we need to calculate the pedestrian density, which is the number of pedestrians per foot of walkway width. To do this, we divide the pedestrian flow (1200) by the effective walkway width (6.5 ft):
Pedestrian density = Pedestrian flow / Effective walkway width
Pedestrian density = 1200 pedestrians / 6.5 ft
Next, we compare the pedestrian density to the standard thresholds for each level of service.
The LOS is a measure of how well the sidewalk is accommodating pedestrian traffic. The thresholds vary depending on the specific guidelines used, but generally, if the pedestrian density is below a certain threshold, it corresponds to a higher level of service.
Based on the given information, we can determine that the pedestrian density is approximately 184.6 pedestrians per foot of walkway width. To determine the LOS, we need to compare this value to the standard thresholds. However, without the specific thresholds provided, we cannot determine the exact LOS.
In conclusion, based on the given information, we can calculate the pedestrian density, but without the specific thresholds, we cannot determine the plantation adjusted LOS.
Learn more about pedestrian flow from the given link!
https://brainly.com/question/14454340
#SPJ11
who plays forza horizon 3
Answers
Answer:
I recently got it on my xbox
Step-by-step explanation:
I usually play with the family my name on xbox is wood
Answer:
me
Step-by-step explanation:
In the xy-plane, a circle with center at point (6,-8) has a radius of 20 units. If the radius of the circle is halved, which of the following points will NOT be inside the circle?
A) (-1/20 , 0)
B) (1/20 , 0)
C) (-1/10 , -6)
D) (8 , 10)
Answers
There is a circle with the center \((6,-8)\) and radius = \(20\) units
We have to find whether the points given in the options will not lie inside the circle if the radius of the circle is halved.
"If a point lies inside the circle, distance between the center and the given point will be less than the radius of the circle".
To find the distance between two points \((x_1,y_1)\) and \((x_2,y_2)\) is given by,
Distance = \(\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
If a point lies inside the circle with radius 10 units, distance between the point and the center will be less than 10 units.
Option A
Distance between the points \((-\frac{1}{20},0)\) and \((6, -8)\)
= \(\sqrt{(6+\frac{1}{20})^2+(-8-0)^2}\)
= \(\sqrt{100.6025}\)
= \(10.03\) units
Since, \(10.03>10\) units
Therefore, \((-\frac{1}{20},0)\) will lie outside the circle.
Option B
Distance between \((\frac{1}{20},0)\) and \((6,-8)\) = \(\sqrt{(6-\frac{1}{20})^2+(-8-0)^2}\)
= \(\sqrt{99.4025}\)
= \(9.97\) units
Since, \(9.97<10\) units
Therefore, \((\frac{1}{20},0)\) will lie inside the circle.
Option C
Distance between \((-\frac{1}{10},-6)\) and \((6,-8)\) = \(\sqrt{(6+\frac{1}{10})^2+(-6+8)^2}\)
= \(\sqrt{41.21}\)
= \(6.42\) units
Since, \(6.42<10\) units
Therefore, \((-\frac{1}{10},-6)\) will lie inside the circle.
Option D
Distance between \((8,10)\) and \((6,-8)\) = \(\sqrt{(8-6)^2+(10+8)^2}\)
= \(\sqrt{328}\)
= \(18.11\) units
Since, \(18.11>10\) units
Therefore, \((8, 10)\) will lie outside the circle.
Now we can conclude that \((-\frac{1}{20},0)\) and \((8,10)\) will lie outside the circle.
Options (A) and (D) will be the correct options.
Learn more about the distance between two points,
https://brainly.com/question/3716231
Calculate the Mean Absolute Percent Error (MAPE) from the following dataset for 6 days: Demand: 16, 19, 21, 21, 22, 17 and Forecast: 20, 20, 20, 20, 20, 20 respectively for each day.
a.
7%
b.
9%
c.
11%
d.
13%
)e.
15%
Answers
c. 11%. This means that the average forecasted demand deviates from the actual demand by approximately 11%.
The Mean Absolute Percent Error (MAPE) measures the accuracy of a forecast by calculating the percentage difference between the actual demand and the forecasted demand. To calculate the MAPE, you can follow these steps:
1. Calculate the absolute percent error (APE) for each day by subtracting the forecasted demand from the actual demand, taking the absolute value of the difference, and dividing it by the actual demand. Here are the APE values for each day:
Day 1: |(16-20)/16| = 20%
Day 2: |(19-20)/19| = 5.26%
Day 3: |(21-20)/21| = 4.76%
Day 4: |(21-20)/21| = 4.76%
Day 5: |(22-20)/22| = 9.09%
Day 6: |(17-20)/17| = 17.65%
2. Calculate the mean of the APE values by summing them up and dividing by the total number of days:
(20% + 5.26% + 4.76% + 4.76% + 9.09% + 17.65%)/6 ≈ 10.98%
3. Finally, multiply the mean APE by 100 to convert it into a percentage. This gives us the MAPE:
10.98% * 100 = 10.98%
Therefore, the MAPE for the given dataset is approximately 10.98%.
c. 11%. This means that the average forecasted demand deviates from the actual demand by approximately 11%.
To know more about dividing visit ;
https://brainly.com/question/15381501
#SPJ11
Pretest: Unit 8
Question 12 of 13
Which option below provides the best description of the relationship between
a quadratic parent function and a square root parent function?
A. The square root function is the quadratic function reflected across
the y-axis.
B. The square root function is the quadratic function reflected across
the line y = x, with a limited domain.
C. The square root function is the quadratic function reflected across
the x-axis.

Answers
The square root function is the quadratic function reflected across.
We have given that,
a quadratic parent function and a square root parent function
A. The square root function is the quadratic function reflected across
the y-axis.
B. The square root function is the quadratic function reflected across
the line y = x, with a limited domain.
C. The square root function is the quadratic function reflected across
the x-axis.
We have to determine the correct option.
What is the parent function?
A parent function is the simplest function of a family of functions that preserves the definition of the entire family.
The correct option is,
B. The square root function is the quadratic function reflected across.
the line y = x, with a limited domain.
graph y=x^2 and y=√x and y=x
graph is attached
To learn more about the graph of function visit:
https://brainly.com/question/4025726
SPJ1

Show that the equation x ^ 3 + 6x - 10 = 0 has a solution between x = 1 and x = 2
Answers
So all we have to do is plug in 1 and 2 for x and prove one is negative and the other is positive.
If we plug in 1, we get -3. If we plug in 2, we get positive 10. This means there is a solution!

Find the volume V of the solid obtained by rotating the region bounded by the given curves about the specified line: 4x2, x = 5, Y = 0; about the Y-axis 49
Answers
The volume of the solid obtained by rotating the region bounded by the given curves about the specified line is 5000 cubic units.
The formula for calculating the volume of a solid obtained by rotating the region bounded by the given curves about the specified line is given by;
V = π ∫[a,b] (f(x))²dx
where f(x) is the function of the curve and a,b are the limits of integration of x.
Using the formula, we have;
The given curves are
4x²,
x = 5,
and
y = 0
and the specified line is the Y-axis.
The region bounded is shown below;
The graph above shows that the region is bounded between
x = 0
and
x = 5.
Therefore, we have;
∫[0,5] (4x²)²dx
= ∫[0,5] 16x^4dx
∫[0,5] 16x^4dx
= 16[ x⁵/5 ]ₓ
=0ₓ
=5
∫[0,5] 16x^4dx
= 16[(5)⁵/5] - 16[(0)⁵/5]
∫[0,5] 16x^4dx
= 16(3125/5) - 0
∫[0,5] 16x^4dx
= 5000
Therefore, the volume of the solid obtained by rotating the region bounded by the given curves about the specified line is 5000 cubic units.
The answer is 5000.
To know more about volume visit:
https://brainly.com/question/28058531
#SPJ11
Determine whether or not each indicated set of 3x3 matrices isa subspace of M33.
The set of all symmetric 3x3 matrices (that is, matricesA=[aij] such that aij = aji for1<= i <= 3, 1<=jj<=3.)
Answers
The set of all symmetric 3x3 matrices satisfies all three conditions for a subspace, it is indeed a subspace of M33
To determine whether the set of all symmetric 3x3 matrices is a subspace of M33, we need to check if it satisfies the three conditions for a subspace:
Closure under addition: If A and B are both symmetric 3x3 matrices, then A+B will also be a symmetric 3x3 matrix since \((A+B)^T = A^T + B^T = A + B\). Therefore, the set is closed under addition.
Closure under scalar multiplication: If A is a symmetric 3x3 matrix and c is a scalar, then cA will also be a symmetric 3x3 matrix since \((cA)^T = cA^T = cA\). Therefore, the set is closed under scalar multiplication.
Contains the zero vector: The zero vector in M33 is the matrix of all zeroes. This matrix is also a symmetric 3x3 matrix since all its entries are equal. Therefore, the set contains the zero vector.
Since the set of all symmetric 3x3 matrices satisfies all three conditions for a subspace, it is indeed a subspace of M33.
For more such questions on matrices
https://brainly.com/question/27929071
#SPJ11
Determine the remainder if
(x3 + 4x - 24) is divided by
(x - 2).
Answers
When \(x^3\)+4x-24 is divided by x-2 then the remainder is -8.
What is remainder theorem?
Remainder Theorem is a method for dividing polynomials according to Euclidean geometry. This theorem states that when a polynomial P(x) is divided by a factor (x - a), which isn't really an element of the polynomial, a smaller polynomial is produced along with a remainder. The remainder theorem asserts that when a polynomial p(x) is divided by (x - a), the remainder equals f. (a). Using Euclid's Division Lemma, this may be demonstrated. To put it another way, p(x) = q(x) (x - a) + r if q(x) is the quotient and 'r' is the remainder.
Here the given \(x^3\)+4x-24 and x-2
When a function f(x) is divided by x+a, then the remainder is given by f(−a):
So, in this case remainder will be f(2) .
=> f(x)= \(x^3\)+4x-24
put x=2 then
=> f(2)= \(2^3\)+4(2)-24
=> f(2) =8+8-24
=> f(2) = 16-24 =-8
Hence the remainder is -8.
To learn more about remainder theorem refer the below link
https://brainly.com/question/13328536
#SPJ9
Consider the expressions (3m + 2n - 6 and (-4-6m + 7n).
What is the sum of the expressions for n=-2 and m=5?
Answers
Answer:
-43
Step-by-step explanation:
The sum of the expression (3m+2n-6) and (-4-6m+7n) when m = 5 and n = -2 is -43.
What is an expression?An algebraic expression consists of unknown variables, numbers and arithmetic operators.
Given are two expressions, (3m+2n-6) and (-4-6m+7n)
Putting m = 5 and n = -2, we get,
(3m+2n-6) = 3x5-2x2-6 = 15-4-6 = 15-10 = 5
(-4-6m+7n) = -4-6x5-7x2 = -4-30-14 = -30-18 = -48
(3m+2n-6) + (-4-6m+7n) = -48+5 = -43
Hence, The sum of the expression (3m+2n-6) and (-4-6m+7n) when m = 5 and n = -2 is -43.
For more references on expression, click;
https://brainly.com/question/14083225
#SPJ2
Q.3) (30 p.) Figure out the solution of each section: A. (10 p.) Obtain Cartesian and polar forms of the function f(z) = z². B. (10 p.) Verify that u(x, y) = (x y³ -x³y) is a harmonic function, and construct the analytic function in the form of w=f(z) = u(x, y) + i v(x, y). C. (10 p.) Find the poles and classify their orders of the following functions: 1 1 1 a. f(z) = ²1 b. f(z) = c. f(z) = z¹ + 2z²+1 z²+z+1
Answers
A. To obtain the Cartesian and polar forms of the function f(z) = z², we square the complex number z and express it in both forms.
B. To verify if u(x, y) = (x y³ -x³y) is a harmonic function, we check if it satisfies Laplace's equation. We can then construct the analytic function w = f(z) = u(x, y) + iv(x, y) by introducing a harmonic conjugate.
C. To find the poles and classify their orders for the given functions, we analyze the denominators and determine the values of z for which the functions become singular.
A. The function f(z) = z² can be expressed in Cartesian form as f(z) = (x + iy)² = x² - y² + 2ixy. In polar form, we write z as z = re^(iθ), where r represents the magnitude and θ is the argument. Squaring z gives f(z) = r²e^(2iθ).
B. To verify if u(x, y) = (x y³ - x³y) is harmonic, we calculate its second-order partial derivatives with respect to x and y. If Laplace's equation (∂²u/∂x² + ∂²u/∂y² = 0) holds true, then u is harmonic.
Next, we introduce a harmonic conjugate v(x, y) such that vₓ = -uₓ and vᵧ = -uᵧ. Solving these partial differential equations gives us v(x, y) = -(x³ + 3xy²) + C, where C is a constant.
Thus, the analytic function w = f(z) = u(x, y) + iv(x, y) is given by w = (x y³ - x³y) - i(x³ + 3xy²) + C.
C. To find the poles and classify their orders for the given functions:
f(z) = ²1: There is no denominator, so the function has no poles.
f(z) = z¹ + 2z² + 1: The denominator is z² + z + 1, which can be factored as (z - ω)(z - ω²), where ω is a complex cube root of unity. The function has simple poles at z = ω and z = ω², with orders 1.
f(z) = z² + z + 1: The denominator is z² + z + 1, which does not factor further. The function has no poles.
By analyzing the denominators of the functions, we determine the poles and classify their orders accordingly.
Learn more about Laplace's equation here :
https://brainly.com/question/31583797
#SPJ11
Exercises: Find the centroid of the solid generated by revolving the region about the indicated axis the area bounded by the given curves. 1. y2 = x, y = 3, x = 0; about the y-axis 2. x2 = y, x = 3, y
Answers
x_bar = (1/V)∫(∫xdA)*dy
y_bar = (1/V)∫(∫ydA)*dy
where V is the volume of the solid and dA is the differential area element.
To evaluate the integrals, we need to convert the equations of the curves into polar coordinates. From y^2 = x, we have x = y^2, and since y = 3 is a horizontal line, we can write y = 3cosθ. Thus, the region can be described by:
0 ≤ θ ≤ π/2
0 ≤ r ≤ 3cosθ
0 ≤ z ≤ r^2sinθ
The volume of the solid can be computed as follows:
V = ∫(∫(r^2sinθ)rdr)*dθ from 0 to π/2
= (1/3)*[r^4sinθ] from 0 to π/2
= (1/3)*[81 - 0] = 27
Now we can compute the x-coordinate of the centroid:
x_bar = (1/V)∫(∫xdA)*dy
= (1/27)∫(∫r^3cosθsinθrdr)dθdy
= (1/27)∫(∫r^4cosθsinθ)dθdy from 0 to 3cosθ
= (1/27)∫(∫r^4cosθsinθ)3cosθdθ from 0 to π/2
= (1/27)[∫(sinθcosθ)[81/5r^5] from 0 to 3cosθ] dθ from 0 to π/2
= (1/27)[27/5(4/5)] = 8/25
Therefore, the x-coordinate of the centroid is 8/25.
To find the y-coordinate of the centroid, we use the formula:
y_bar = (1/V)∫(∫ydA)*dy
= (1/27)∫(∫r^3cosθsinθrdr)dθdy
= (1/27)∫(∫r^4cosθsinθ)dθdy from 0 to 3cosθ
= (1/27)∫(∫r^4cosθsinθ)3cosθdθ from 0 to π/2
= (1/27)[∫(sinθcosθ)[81/5r^5] from 0 to 3cosθ] dθ from 0 to π/2
= (1/27)[27/5(27/8)] = 9/40
Therefore, the y-coordinate of the centroid is 9/40.
Hence, the centroid of the solid generated by revolving the region y^2 = x, y = 3, and x = 0 about the y-axis is (8/25, 9/40, 0).
2. To find the centroid of the solid generated by revolving the region bounded by the curves x^2 = y and x = 3 about the y-axis, we again need to use the formula:
x_bar = (1/V)∫(∫xdA
Learn more about centroid, here:
brainly.com/question/29633268
#SPJ11
if there are 10 people per race, and 2222 people have come in first place, then how many races have happened?
Answers
Answer:
22,220
Step-by-step explanation:
Because you multiply by 10 because 2222 times 1 is 1 person per race, so if there is 10 then you multiply by 10.
The variables a and b are proportional. When a=12 we
know b=3. What is the value of a when b=5?
O 17
9
20
O 14

Answers
Answer:
b = 20
Step-by-step explanation:
the variables a and b are proportional , so the equation relating them is
a = kb ← k is the constant of proportion
to find k use the condition a = 12 , b = 3
12 = 3k ( divide both sides by 3 )
4 = k
a = 4b ← equation of proportion
when b = 5 , then
a = 4 × 5 = 20
Let u = <-4, 3>. Find the unit vector in the direction of u, and write your answer in component form. (2 points)
Answers
Answer: < -4/5, 3/5>
This is equivalent to writing < -0.8, 0.6 >
======================================================
Explanation:
Draw an xy grid and plot the point (-4,3) on it. Draw a segment from the origin to this point. Then draw a vertical line until reaching the x axis. See the diagram below.
We have a right triangle with legs of 4 and 3. The hypotenuse is \(\sqrt{4^2+3^2} = \sqrt{16+9} = \sqrt{25} = 5\) through use of the pythagorean theorem.
We have a 3-4-5 right triangle.
Therefore, the vector is 5 units long. This is the magnitude of the vector.
Divide each component by the magnitude so that the resulting vector is a unit vector pointing in this same direction.
Therefore, we go from < -4, 3 > to < -4/5, 3/5 >
This is equivalent to < -0.8, 0.6 > since -4/5 = -0.8 and 3/5 = 0.6
Side note: Unit vectors are useful in computer graphics.

Anthony is rowing a boat upstream. The following equation models his speed: f(x) = 3x2 − 6x − 13, where x is the velocity of the boat relative to land. What is the domain of the function? (1 point)
Answers
The domain of the function f(x) = 3x^2 - 6x - 13 is (-∞, ∞).
The domain of a function is the set of values that we are allowed to plug into our function. This set is the x values in a function such as f(x). The range of a function is the set of values that the function assumes.
To determine the domain of the function f(x) = 3x^2 - 6x - 13, we need to consider any restrictions on the values of x that would make the function undefined.
In this case, since x represents the velocity of the boat relative to land, there are no inherent limitations or restrictions on the possible values of x. The domain of the function is therefore all real numbers, or (-∞, ∞).
Therefore, the domain of the function f(x) = 3x^2 - 6x - 13 is (-∞, ∞).
For such more questions on Domain
https://brainly.com/question/1045262
#SPJ8
Why is estimation useful when finding actual products
and solving real-world problems?

Answers
Answer:
Estimation is useful when finding actual products and real world solving because, it leads you closer to the answer you are going to be aiming for. For example if a question is 23 x 6 + 1= ? you would estimate around the 100 because it is closer to the answer you will mostly likely create and get.
Hope this helps :3
Answer:
Estimation is useful when finding actual products and real world solving because, it leads you closer to the answer you are going to be aiming for. For example if a question is 23 x 6 + 1= ? you would estimate around the 100 because it is closer to the answer you will mostly likely create and get.
Step-by-step explanation:
what are all the values of c that will make x^2 cx 121 a perfect square ?
Answers
Answer:
c = -22, 22
Step-by-step explanation:
\( {(x - 11)}^{2} = {x}^{2} - 22x + 121\)
\( {(x + 11)}^{2} = {x}^{2} + 22x + 121\)
FOR BRAINLIEST PLS ANSWER THIS ASAP! with complete solution pls. Thank you in advance

Answers
By using the formula for area of triangle using coordinates, the following results are obtained
13) Area of triangle = \(\frac{15}{2} \ sq. units\)
14) Area of triangle = \(\frac{49}{2} \ sq. units\)
What is area of triangle?
Area of a triangle is the total space taken by the triangle. If the coordinates of triangle are \((x_1, y_1), (x_2, _2) \ and \ (x_3, y_3)\), then area of triangle is calculated by the formula
Area of triangle = \(\frac{1}{2}|x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|\)
13) The given coordinates are E (3, 1), F(3, -2) and G(-2, 2)
Area of triangle =
\(\frac{1}{2}|3(-2-2) + 3(2-1) + (-2)(1 -(-2))|\\\\\frac{1}{2}|3(-4) + 3(1) -2(3)|\\\\\frac{1}{2}|-12 + 3 - 6|\\\\\frac{1}{2}|-15|\\\\\frac{15}{2} \ sq. units\)
14) The given coordinates are E (-3, 4), F(4, 4) and G(3, -3)
Area of triangle =
\(\frac{1}{2}|(-3)(4-(-3)) + 4(-3-4) + 3(4-4)|\\\\\frac{1}{2}|(-3)(7)+4(-7)+3(0)]\\\\\frac{1}{2}|-21-28+0|\\\\\frac{1}{2}|-49|\\\\\frac{49}{2} \ sq. units\)
To learn more about area of triangle, refer to the link-
https://brainly.com/question/17335144
#SPJ1
Split £20 in the ratio 2:3
Answers
Hi friend,
The objective is to divide $20 in 2:3 ratio.
One part be 2x, another part is 3x
Sum of them = 20
2x + 3x = 20
5x = 20
x=4
So therefore one part must be 2x = 2 x 4 = 8
Another part = 3x = 3 x 4 = 12
Hence it is divided in 2:3 ratio.
Hope my answer is helpful to u. :)