Answers
Answer:
(0,2)
Step-by-step explanation:
2:4 means one part is 2/(2+4)=1/3 of AB and the other part is 2/3 of AB
Add 1/3 of the distance from -2 to 4. (1/3)(4+2)=2. -2+2=0 The x coordinate is 0
Subtract 1/3 of the distance from 6 to -6, (1/3)6+6)=4 6-4=2 The y coordinate is 2
The point is (0,2)
Related Questions
Ana invests $500 into a bank account for 18 months. At the end of the 18 months she would have earned $52.50 in interest. At what rate did she earn interest on her investment?
Answers
Answer:
2.95 i think
Step-by-step explanation:
Chau, a highway safety inspector, is concerned about the potential for accidents caused by boulders that fall down a sandstone cliff beside a main highway.

Answers
The percentage of weights between 493 kg and 681 kg is given as follows:
64.12%.
How to obtain probabilities using the normal distribution?The z-score of a measure X of a variable that has mean symbolized by \(\mu\) and standard deviation symbolized by \(\sigma\) is obtained by the rule presented as follows:
\(Z = \frac{X - \mu}{\sigma}\)
The z-score represents how many standard deviations the measure X is above or below the mean of the distribution, depending if the obtained z-score is positive or negative.Using the z-score table, the p-value associated with the calculated z-score is found, and it represents the percentile of the measure X in the distribution.The mean and the standard deviation for this problem are given as follows:
\(\mu = 565, \sigma = 100\)
The proportion of of weights between 493 kg and 681 kg is the p-value of Z when X = 681 subtracted by the p-value of Z when X = 493, hence:
X = 681:
Z = (681 - 565)/100
Z = 1.16
Z = 1.16 has a p-value of 0.877.
X = 493:
Z = (493 - 565)/100
Z = -0.72
Z = -0.72 has a p-value of 0.2358.
Hence:
0.8770 - 0.2358 = 0.6412 = 64.12%.
More can be learned about the normal distribution at https://brainly.com/question/25800303
#SPJ1
Question 15The expression, 81x^2 + bx + 36, is a perfect square trinomial.Give the value of b: Factor the expression as a perfect square:
Answers
We can factor a perfect square trinomial as a perfect square like this:
\(A^2+2AB+B^2=(A+B)^2\)Now, we have to find the values of A and B in our trinomial: 81x^2+bx+36, by making it look like the general above general form.
As we can see:
\(\begin{gathered} A^2+2AB+B^2=81x^2+bx+36 \\ \text{then:} \\ A^2=81x^2 \\ \text{then:} \\ A=\sqrt[]{81x^2}=\sqrt[]{81}\times\sqrt[]{x^2}=9x \\ \text{And} \\ B^2=36 \\ \text{Then:} \\ B=\sqrt[]{36}=6 \end{gathered}\)Now we know that:
\(\begin{gathered} bx=2\times A\times B=2\times9x\times6=2\times9\times6\times x=108x \\ \text{then:} \\ \frac{bx}{x}=\frac{108x}{x} \\ b=108 \end{gathered}\)And, when we factor our perfect square trinomial as a perfect square it looks like this:
\((9x+6)^2\)Consider a circle whose equation is x2 + y2 – 2x – 8 = 0. Which statements are true? Select three options.
The radius of the circle is 3 units.
The center of the circle lies on the x-axis.
The center of the circle lies on the y-axis.
The standard form of the equation is (x – 1)² + y² = 3.
The radius of this circle is the same as the radius of the circle whose equation is x² + y² = 9.
Answers
The three statements that are true include the following:
A. The radius of the circle is 3 units.
B. The center of the circle lies on the x-axis.
D. The radius of this circle is the same as the radius of the circle whose equation is x² + y² = 9.
What is the equation of a circle?In Mathematics, the standard form of the equation of a circle is represented by this mathematical expression;
(x - h)² + (y - k)² = r² .......equation 1.
Where:
h and k represents the coordinates at the center of a circle.
r represents the radius of a circle.
Based on the information provided, we have the following equation of a circle:
x² + y² – 2x – 8 = 0 ......equation 2.
In order to determine the true statements, we would rewrite the equation in standard form and then factorize by using completing the square method:
x² – 2x + y² = 8 = 0
x² – 2x + (2/2)² + y² = 8 + (2/2)²
x² – 2x + 1 + y² = 8 + 1
(x – 1)² + (y - 0)² = 9 .......equation 3.
By comparing equation 1 and equation 3, we have the following:
Center (h, k) = (1, 0)
Radius (r) = 3
Additionally, this line and the center of the given circle lies on the x-axis (x-coordinate) because the y-value is equal to zero (0).
(x - 0)² + (y - 0)² = 3²
x² + y² = 9.
Read more on equation of a circle here: brainly.com/question/17028215
#SPJ1
which expression is a cube root of -2i?

Answers
The cube root of -2i,
⇒ ∛2[ cos(π/6) + i sin(π/6) ]
We can represent -2i in polar form as,
r(cosθ + i sinθ)
by computing its magnitude and angle.
The magnitude of -2i is 2
Since the absolute value of any imaginary number is equal to its magnitude.
To find the angle θ,
We can use the fact that the tangent of an angle is equal to the ratio of the opposite side to the adjacent side.
In this case,
The opposite side is -2 and the adjacent side is 0.
Therefore, we have tanθ = -2/0, which is undefined.
However,
We can use the fact that the cube root of a complex number is equal to the cube root of its magnitude times exp(iθ/3) to find the cube root of -2i.
So, the cube root of -2i is equal to the cube root of 2 times exp(iθ/3).
Now, we need to find the value of θ/3. Since θ is undefined,
we will represent it as π/2 + 2πn,
where n is any integer.
So, θ/3 = (π/2 + 2πn)/3 = π/6 + 2πn/3.
Therefore, the cube root of -2i is equal to
⇒ ∛2 [ cos(π/6 + 2πn/3) + i sin(π/6 + 2πn/3) ]
Now put n = 0
⇒ ∛2[ cos(π/6) + i sin(π/6) ]
This is the final form of the cube root of -2i in the required form.
To learn more about complex numbers visit:
https://brainly.com/question/27940074
#SPJ1
WILL GIVE BRAINLIEST! Simplify the expression: 1.2m^(4-n) *0.5m^(n+6)
Answers
Answer:
0.6m^(10)
Step-by-step explanation:
1.2m^(4-n) *0.5m^(n+6)
Regroup
(1.2 * 0.5) * m^(4 - n) * m^(n + 6)
When multipling numbers with the same base, sum the exponents
0.6m^(10)
Which triangle is a reflection of the green triangle
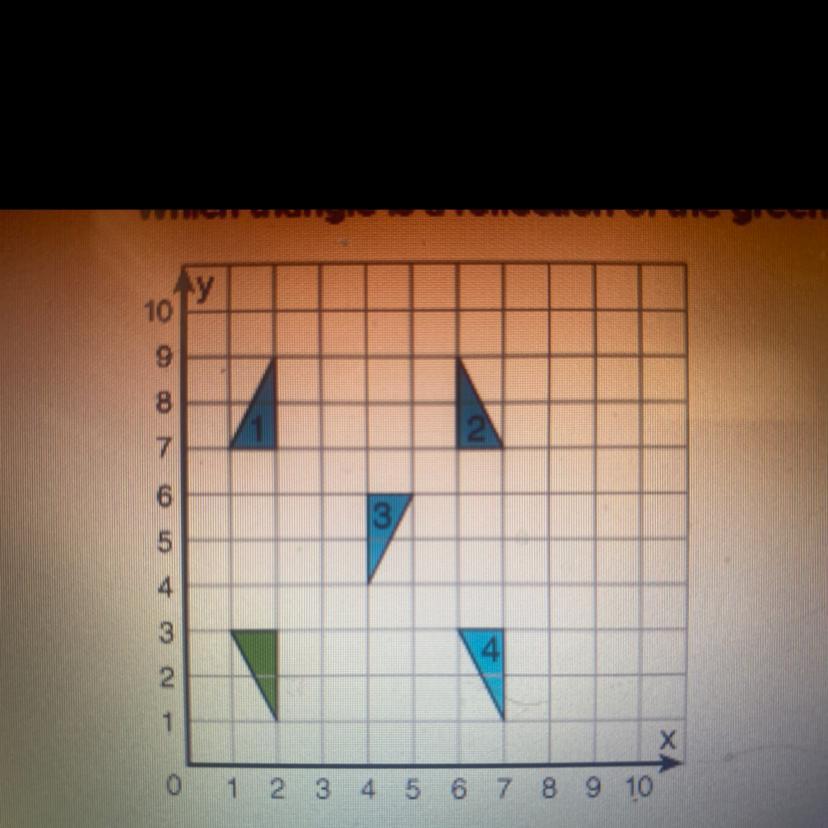
Answers
Tthe triangle that is a reflection of the green triangle is figure 1
Which triangle is a reflection of the green triangleFrom the question, we have the following parameters that can be used in our computation:
The figures
Where, we have:
Figure 1 and the green figure have the opposite orientationFigure 1 and the green figure have the same sizeThis means that the triangle that is a reflection of the green triangle is figure 1
Read more about transformation at
brainly.com/question/4289712
#SPJ1
50! POINTS! HELP QUICK!
Which of the following is the equation for the graph shown?
y squared over 4 minus x squared over 12 equals 1
y squared over 16 minus x squared over 12 equals 1
x squared over 4 minus y squared over 12 equals 1
x squared over 16 minus y squared over 12 equals 1
50 points!

Answers
|3y - 7| - 10 = -5 solve for y:
Answers
Answer: y=1.25
Step-by-step explanation:
First things first you have to find what is in the bracket things (i don’t know what it’s called) So 3 - 7 is -4y but since it’s absolute it’s going to be 4y.
So now you’ve got 4y - 10 = -5. Your going to want to eliminate 10 so, subtract 10 to both sides giving you 4y = -5
Lastly to get y by itself you need to divide it by its self so, 4y divided by 4. Do it to both sides. This gives you…
Y = 1.25
is -81,572 ratonal or irrational
Answers
Answer:
rational
Step-by-step explanation:
as it is of the form p/q
mark me as brainliest ❤️
a square as an area of 144m 2 squared what is the length of each side
Answers
Answer:
12
Step-by-step explanation:
To find the area of a square, you have to square a side length. Squaring a number is the same as multiplying a number by itself.
12 x 12 = 144
-17( -18r-16)
Please show your work!
Answers
Answer:
Step-by-step explanation:

Answer: 306r + 272
Step-by-step explanation:
To simplify the expression -17(-18r-16), we can use the distributive property of multiplication, which states that:
a(b+c) = ab + ac
Using this property, we can expand the expression as follows:
-17(-18r-16) = (-17) x (-18r) + (-17) x (-16)
Multiplying the coefficients:
= 306r + 272
Therefore, -17(-18r-16) simplifies to 306r + 272.
50 Points!!! Solve each inequality. Then graph the solution set on a number line. Photo attached

Answers
50
Step-by-step explanation:
plot it on the number line
Nicks lunch cost $14.75 tax was 1.03 and he left a tip of 2.50 how much did he pay for his lunch
Answers
Answer:
$18.28
Step-by-step explanation:
To complete this problem is a straightforward answer:
First, you add 14.75 + 1.03 which equals $15.78 then, you'll want to add 2.50 to 15.78 and there you have your answer!!
Three quarters of a number is 27. What is two ninths of the number?
Answers
Answer:
8
Step-by-step explanation:
let x be the number , then
\(\frac{3}{4}\) x = 27 ( multiply both sides by 4 to clear the fraction )
3x = 108 ( divide both sides by 3 )
x = 36
the number is 36, so
\(\frac{2}{9}\) × 36 = 2 × 4 = 8
The two ninths of the number is 8
We know that Three quarters of a number is \(\frac{3}{4}\) times of a number
Hence we will assume the number x ,
\(\frac{3}{4} of x = 27\)
\(x = 27 X \frac{4}{3}\)
\(x = 36\)
Now as we know the number is 36
Therefore , the two ninths of the number assumed as y
We will multiply the number 36 by 2 and then divide by 9
Hence,
\(y = 36 X \frac{2}{9}\)
\(y = 8\)
Thus, the two ninths of the number 36 is 8
Practice more quarters related questions
https://brainly.in/question/13325111
The balance in your bank account is $720.50. You use your debit card for purchases of $45, $82, and $22.25. Then, you deposit $98.45 in the account. What is the new balance of your account?
Answers
Answer:
669 dollars and 70 cents
Step-by-step explanation:
just minus all the money spent and add the money added
f(x)=(-3x^2-1)/3x^3 does f have an inverse function?
Answers
Answer: Yes, Probably
6= 2(y+2). Helppppppppppppppp
Answers
Answer:
y=1
Step-by-step explanation:
6=2y+4
2=2y
y=1
The heights of adult men in America are normally distributed, with a mean of 69.8 inches and a standard deviation of 2.69 inches. The heights of adult women in America are also normally distributed, but with a mean of 64.1 inches and a standard deviation of 2.55 inches.
Required:
a. If a man is 6 feet 3 inches tall, what is his z-score (to two decimal places)?
b. What percentage of men are SHORTER than 6 feet 3 inches?
c. If a woman is 5 feet 11 inches tall, what is her z-score (to two decimal places)?
d. What percentage of women are TALLER than 5 feet 11 inches?
Answers
Answer:
a) 1.93
b) 97.32% of men are SHORTER than 6 feet 3 inches
c) 2.71
d) 0.34% of women are TALLER than 5 feet 11 inches
Step-by-step explanation:
When the distribution is normal, we use the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
a. If a man is 6 feet 3 inches tall, what is his z-score (to two decimal places)?
For man, \(\mu = 69.8, \sigma = 2.69\)
A feet has 12 inches, so this is Z when X = 6*12 + 3 = 75. So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{75 - 69.8}{2.69}\)
\(Z = 1.93\)
b. What percentage of men are SHORTER than 6 feet 3 inches?
Z = 1.93 has a pvalue of 0.9732
97.32% of men are SHORTER than 6 feet 3 inches
c. If a woman is 5 feet 11 inches tall, what is her z-score (to two decimal places)?
For woman, \(\mu = 64.1, \sigma = 2.55\)
Here we have X = 5*12 + 11 = 71.
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{71 - 64.1}{2.55}\)
\(Z = 2.71\)
d. What percentage of women are TALLER than 5 feet 11 inches?
Z = 2.71 has a pvalue of 0.9966
1 - 0.9966 = 0.0034
0.34% of women are TALLER than 5 feet 11 inches
A colored chip is yellow on one side and red on the other. The chip was flipped 50 times and landed on red side up 22 times. What is the relative frequency of the chip landing with the red side facing up? (5 points)
A. 36%
B. 44%
C. 52%
Answers
Answer:
b
Step-by-step explanation:
If a=8 and b=5 and x=4 and y=6m -2 what is the value of m ?

Answers
Answer:
m = 2
Step-by-step explanation:
Given:
x = 4
y = 6m - 2
a = 8
b = 5
Required:
Value of m
SOLUTION:
x and y are segments of a chord divided when it intersects another chord that also has segments a and b.
According to the Intersecting chords theorem, \( a*b = x*y \)
Thus:
\( 8*5 = 4*(6m - 2) \)
Solve for m
\( 40 = 24m - 8 \)
\( 40 + 8 = 24m - 8 + 8 \)
\( 48 = 24m \)
\( \frac{48}{24} = \frac{24m}{24} \)
\( 2 = m \)
The value of m = 2
Which describes the turn the angle on the circle shows?

Answers
2 f(x)=x2 + 2x cómo se evalúa?
a) f(3)
b) f(-1)
c) f(x-3)
Answers
Answer:
b) f (-1) ese es el resultado
In this problem, we explore the effect on the mean, median, and mode of multiplying each data value by the same number. Consider the following data set.
4, 4, 5, 8, 12
Answers
The mean is 6.6, the median is 5 and the mode is 4
How to determine the mean, median, and mode?The dataset is give as:
4, 4, 5, 8, 12
The mean is calculated as:
Mean = Sum/Count
So, we have:
Mean = (4 + 4 + 5 + 8 + 12)/5
Evaluate
Mean = 6.6
The median is the middle number.
Here, the middle number is 5
So, we have:
Median = 5
The mode is the number with the highest frequency
Here, 4 has the highest frequency
So, we have:
Mode = 4
Hence, the mean is 6.6, the median is 5 and the mode is 4
Read more about mean, median and mode at:
https://brainly.com/question/14532771
#SPJ1
9.
Identify the vertex of the parabola.
A. (−2, −1)
B. (−1, −2)
C. (1, 2)
D. (−3, 2)

Answers
I’m this case, the lowest point
Solution: (-1, -2)
Answer:
(-1,-2) based on the graph
Step-by-step explanation:
Consider the line y 2x - 4.Find the equation of the line that is parallel to this line and passes through the point (-3,-4).Find the equation of the line that is perpendicular to this line and passes through the point (-3,-4).Note that the ALEKS graphing calculator may be helpful in checking your answer.

Answers
The question asks us to consider the following equation of a line:
\(y=2x-4\)We are asked to find the line parallel to this line.
First of all, we need to know the condition for two lines to be parallel.
If two lines are given by the equations:
\(\begin{gathered} y_{}=m_1x+c_1\text{ (Line 1)} \\ y=m_2x+c_2\text{ (Line 2)} \\ \text{where,} \\ m_1,m_2=\text{slopes of lines 1 and 2 respectively} \\ c_1,c_2=y-\text{intercept of lines 1 and 2 respectively} \end{gathered}\)For the two lines to be parallel, we would have:
\(\begin{gathered} m_1=m_2 \\ i\mathrm{}e\text{. the slopes of both lines must be equal} \end{gathered}\)Now, that we have this, we can find the first parallel line.
This is done below:
\(\begin{gathered} \text{ Comparing the equation in the question to the general} \\ \text{form of a line to get the slope:} \\ y=mx+c\equiv y=2x-4 \\ \therefore m=2,c=-4 \\ \text{ Hence, the slope is m = 2} \\ \\ By\text{ the condition for parallel lines, we can s}ee\text{ that the parallel } \\ \text{ line to the equation given in the question will also have:} \\ m=2\text{ as its slope} \end{gathered}\)Therefore, the parallel line will have the form:
\(\begin{gathered} y=2x+c \\ \end{gathered}\)We don't know c yet. We are told that this line passes through the point (-3, -4). Hence, to get
c, we simply substitute these points into the incomplete equation above.
This is done below:
\(\begin{gathered} y=2x+c \\ \text{ Using the point (-3, -4),} \\ x=-3,y=-4 \\ -4=2(-3)+c \\ -4=-6+c \\ \text{add 6 to both sides} \\ -4+6=-6+6+c \\ 2=c,c=2 \end{gathered}\)Therefore, the parallel line equation is given by:
\(y=2x+2\)For the perpendicular lines, the condition to be used is:
\(\begin{gathered} m_1=-\frac{1}{m_2} \\ \text{where,} \\ m_1,m_2\text{ are the slopes of the perpendicular lines} \end{gathered}\)Since we know the slope of the line given in the question is m = 2, therefore, the slope for the line perpendicular to it is given by:
\(m_2=-\frac{1}{2}\)We can now compute the perpendicular line as:
\(\begin{gathered} y=mx+c \\ y=-\frac{1}{2}x+c \end{gathered}\)We still need to find the y-intercept (c) of the perpendicular line. In order to do this, we simply substitute the point (-3, -4) which the perpendicular line passes through into the above incomplete equation to find c.
This is done below:
\(\begin{gathered} y=-\frac{1}{2}x+c \\ \text{choosing point (-3, -4)} \\ x=-3,y=-4 \\ -4=-\frac{1}{2}(-3)+c \\ -4=\frac{3}{2}+c \\ \text{subtract 3/2 from both sides} \\ -4-\frac{3}{2}=\frac{3}{2}-\frac{3}{2}+c \\ \therefore c=-4-\frac{3}{2} \\ \\ c=-\frac{11}{2} \end{gathered}\)Hence, the perpendicular line equation is:
\(y=-\frac{1}{2}x-\frac{11}{2}\)Therefore the final answers are:
Parallel: y = 2x + 2
Perpendicular: y = -x/2 - 11/2
Plotting the graphs, they look like this:

Factor 4x2 + 24x + 36.
A) 4(x + 3)(x + 3)
B) 4(x + 6)(x – 6)
C) (4x + 3)(x + 3)
D) (2x – 6)(2x – 6)
Answers
Answer:
\(\huge\boxed{\text{A) } 4(x+3)(x+3) }\)
Step-by-step explanation:
In order to factor this, we need to factor out a common term and then solve for x.
We can see that we can factor out a 4 from this entire equation as each term is a multiple of 4.
This leaves us with \(4(x^2+ 6x + 9)\).
We can now solve for x for the expression in the parentheses, \(x^2 +6x + 9\).
To solve for x, we can use the XBOX method. This tells us that:
When the two roots are added, they will equal b (in this case, 6) When the two roots are multiplied, they will equal c (in this case 9)Experimenting with some numbers gets us with 3 and 3 - 3+3 = 6 and 3*3 = 9.
Therefore, our roots will be \((x+3)(x+3)\).
Putting that back into the factorization of our original expression, that leaves us with \(4(x+3)(x+3)\).
Hope this helped!
The perimeter of a square garden is 12 km. Find its area.
Answers
Answer:
The area of the garden is 9 km²
Step-by-step explanation:
If the garden is a square, that means that it's side length is one fourth of the total perimeter, giving us a length and width of 3km
That means that it's area is 3km × 3km, or 9km²
Find the difference between the actual quotient and the estimated quotient of 54,114÷29 . (Dividend is rounded off to nearest thousand and divisor to nearest ten)
Answers
The difference between the actual quotient and the estimated quotient of 54,114 ÷ 29 is approximately 66.3448275862068965517241379.
To find the difference between the actual quotient and the estimated quotient of 54,114 ÷ 29, we need to first calculate the actual quotient and then the estimated quotient.
Actual quotient:
Dividing 54,114 by 29, we get:
54,114 ÷ 29 = 1,866.3448275862068965517241379 (approximated to 28 decimal places)
Estimated quotient:
Rounding the dividend, 54,114, to the nearest thousand gives us 54,000. Rounding the divisor, 29, to the nearest ten gives us 30. Now, we can perform the division with the rounded values:
54,000 ÷ 30 = 1,800
Difference between actual and estimated quotient:
Actual quotient - Estimated quotient = 1,866.3448275862068965517241379 - 1,800 = 66.3448275862068965517241379
For mor such questions on quotient visit:
https://brainly.com/question/11418015
#SPJ8
how much money deposited now will provide payment of Rs. 15000 at the end of each half year for 10 years, if interest is 16% compounded six-monthly
Answers
The interest is 16% compounded semi-annually, is Rs. 121,179.10.
To determine how much money needs to be deposited now to provide a payment of Rs. 15,000 at the end of each half year for 10 years, we will use the formula for the present value of an annuity.
Present value of an annuity = (Payment amount x (1 - (1 + r)^-n))/rWhere:r = interest rate per compounding periodn = number of compounding periodsPayment amount = Rs. 15,000n = 10 x 2 = 20 (since there are 2 half years in a year and the payments are made for 10 years)
So, we have:r = 16%/2 = 8% (since the interest is compounded semi-annually)Payment amount = Rs. 15,000Using the above formula, we can calculate the present value of the annuity as follows:
Present value of annuity = (15000 x (1 - (1 + 0.08)^-20))/0.08 = Rs. 121,179.10Therefore, the amount that needs to be deposited now to provide payment of Rs. 15,000 at the end of each half year for 10 years, if the interest is 16% compounded semi-annually, is Rs. 121,179.10.
For more such questions on semi-annually
https://brainly.com/question/30573341
#SPJ8
