what's the Side number Bottom number
Answers
Answer:
When you get your blood pressure numbers, there are two of them. The first, or “top” one, is your systolic blood pressure. The second, or “bottom,” one is diastolic blood pressure.
Step-by-step explanation:
Related Questions
When we conclude that the results we have gathered from our sample are probably also found in the population from which the sample was drawn, we say that the results are:
Answers
When we conclude that the results we have gathered from our sample are probably also found in the population from which the sample was drawn, we say that the results are statistically significant.
In statistical analysis, we use hypothesis testing to determine whether the results of a sample are likely to be representative of the population as a whole. If the results are statistically significant, we can infer that there is a low probability that the observed differences between the sample and the population occurred by chance alone.
This allows us to generalize the findings from the sample to the larger population with a reasonable degree of confidence.
Learn more about hypothesis testing
https://brainly.com/question/31199947
#SPJ4
Find the volume of the solid generated by revolving the region bounded on the left by the parabola x =y 2 +1 and on the right by the line x =5 about (a) the x-axis; (b) the y-axis; (c) the line x =5
Answers
To find the volume of the solid generated by revolving the region bounded on the left by the parabola x = y^2 + 1 and on the right by the line x = 5, we will use the method of cylindrical shells.
(a) Revolving about the x-axis:
The radius of each cylindrical shell is the distance from the axis of rotation (x-axis) to the parabola, which is y. The height of each shell is the difference between x = 5 and the parabola x = y^2 + 1.
The volume of each shell is given by V = 2πrh, where r is the radius and h is the height.
Integrating from y = -√5 to y = √5, we have:
V = ∫[√5, -√5] 2πy(y^2 + 1 - 5) dy
= 2π ∫[√5, -√5] (y^3 - 3y) dy
= 2π [y^4/4 - (3/2)y^2] |[√5, -√5]
= 2π [(5√5/4 - (3/2)(5)) - (-5√5/4 - (3/2)(5))]
= 2π [(5√5/4 - 15/2) - (-5√5/4 - 15/2)]
= 2π [(5√5/4 + 15/2) - (5√5/4 + 15/2)]
= 2π (0)
= 0
Therefore, the volume of the solid generated by revolving about the x-axis is 0.
(b) Revolving about the y-axis:
The radius of each cylindrical shell is the distance from the axis of rotation (y-axis) to the parabola, which is x = y^2 + 1. The height of each shell is the difference between x = 5 and x = y^2 + 1.
The volume of each shell is still given by V = 2πrh, where r is the radius and h is the height.
Integrating from y = -√5 to y = √5, we have:
V = ∫[√5, -√5] 2π(y^2 + 1)(5 - (y^2 + 1)) dy
= 2π ∫[√5, -√5] (4y^4 - 4y^2 + 4) dy
= 2π [y^5/5 - (4/3)y^3 + 4y] |[√5, -√5]
= 2π [(5√5/5 - (4/3)(5)) - (-5√5/5 - (4/3)(-5))]
= 2π [(√5 - 20/3) - (-√5 - 20/3)]
= 2π [(√5 - 20/3) + (√5 + 20/3)]
= 2π (2√5/3)
= (4/3)π√5
Therefore, the volume of the solid generated by revolving about the y-axis is (4/3)π√5.
(c) Revolving about the line x = 5:
In this case, the radius of each cylindrical shell is the distance from the axis of rotation (x = 5) to the parabola, which is 5 - (y^2 + 1). The height of each shell is y.
The volume of each shell is still given by V = 2πrh, where r is the radius and h is the height.
Integrating from y = -√5 to y = √5, we have:
V = ∫[√5, -√5] 2π(5 - (y^2 + 1))y dy
= 2π ∫[√5, -√5] (5y - y^3 - y) dy
= 2π [5y^2/2 - y^4/4 - y^2/2] |[√5, -√5]
= 2π [(5(5)/2 - (5/4)(5)) - (5(5)/2 - (5/4)(5))]
= 2π [(25/2 - 25/4) - (25/2 - 25/4)]
= 2π [(25/4 - 25/4) - (25/4 - 25/4)]
= 2π (0)
= 0
Therefore, the volume of the solid generated by revolving about the line x = 5 is 0.
In summary:
(a) Volume about the x-axis: 0
(b) Volume about the y-axis: (4/3)π√5
(c) Volume about the line x = 5: 0
Learn more about parabola here
https://brainly.com/question/29635857
#SPJ11
luka's weekly earnings of $475 are increased by 6% calculate his new weekly earnings
Answers
Determine which of the following reactions can occur. For those that cannot occur, determine the conservation law (or laws) that is violated.a) p−>Π++Π0b) p+p−>p+p+Π0c) p+p−>p+Π+d) Π+−>μ++vμe) n−>p+e−+ve(anti)f) Π+−>μ++n
Answers
a]Cannot occur due to violation of baryon number conservation, b] Can occur, c] Can occur, d] Can occur but violates lepton number conservation, e] Can occur and f] Cannot o cur due to violation of charge and baryon number conservations.
The answer are as follows- a) This reaction can occur as it conserves charge, baryon number, and lepton number.
b) This reaction cannot occur as it violates conservation of charge. The right side has one more positive charge than the left side.
c) This reaction cannot occur as it violates conservation of charge. The left side has zero charge while the right side has one positive charge.
d) This reaction can occur as it conserves charge and lepton number. However, it violates conservation of baryon number as the left side has a baryon number of one while the right side has a baryon number of zero.
e) This reaction can occur as it conserves charge, lepton number, and baryon number.
f) This reaction cannot occur as it violates conservation of charge. The left side has a positive charge while the right side has a neutral charge.
To know more about lepton number refer to-
https://brainly.com/question/4087041
#SPJ11
What is the ordered pair
A -2
B -1
C 0
D 1
E 2
F 1

Answers
Sara could use the following system of inequalities to determine how many of each kind of food She can serve:
6x + 3y <45x> = 4
What is the ordered pair?Generally, For this case we have the following variables:
x = the number of wing servings
y = the number of burgers
We write the system of equations:
"Sara knows that at least 4 of her friends want wings":
x> = 4
"Sara must spend less than $ 45.00":
6x + 3y <45
Read more about ordered pair
https://brainly.com/question/30113488
#SPJ1
The required inequalities are x >= 4 and 6x + 3y< 45
She can serve 4 wings and 6 burgers so she spends less than $45.
How to solveConsider the provided information.
Wings cost $6.00 per serving and burgers are $3.00 each.
x represents the number of wing servings and y represents the number of burgers.
Sara knows that at least 4 of her friends want wings.
Thus x>=4
Sara must spend less than $45.00
6x + 3y< 45
Hence, the required inequalities are x >= 4 and 6x + 3y< 45
Now find how many of each kind of food Sara can serve.
If she serves 4 wings:
6(4) + 3y < 45
y <7
She can serve 4 wings and 6 burgers so she spends less than $45.
Similarly, She can serve 5 wings and 4 burgers, she can serve 6 wings and 2 burger or she can serve 7 wings.
Read more about inequalities here:
https://brainly.com/question/24372553
#SPJ1
. find the volume of the region bounded by the paraboloids z = 12 − x 2 − y 2 and z = 2x 2 2y 2
Answers
The volume of the region bounded by the two paraboloids is 32π/5 cubic units.
How to determine the volume of bounded region?To find the volume of the region bounded by the two paraboloids, we need to determine the limits of integration for each variable.
Since the two paraboloids intersect in a curve, we can use this curve as a boundary to split the region into two parts.
First, let's find the curve of intersection by setting the two equations equal to each other:
\(12 - x^2 - y^2 = 2x^2 + 2y^2\\10x^2 + 10y^2 = 12\\x^2 + y^2 = 6/5\)
This is the equation of a circle with center at the origin and radius \(\sqrt{(6/5)\)
So we can use cylindrical coordinates to integrate over this region.
The limits for z are from the lower paraboloid to the upper paraboloid:
\(2x^2 + 2y^2 \leq z\leq 12 - x^2 - y^2\)
In cylindrical coordinates, we have:
\(0 \leq r \leq \sqrt{(6/5)}\\0 \leq \theta \leq 2\pi \\2r^2 \leq z \leq 12 - r^2\)
So the volume of the region is given by the triple integral:
V = ∫∫∫ dz r dr dθ
where the limits of integration are as described above. Therefore, we have:
\(V = \int\limits^{2\pi }_0 {\int\limits^{\sqrt{6/5}}_0 {\int\limits^{12-r^2}_{2r^2} \, dz}\ r \, dr } \, d\theta\)
Evaluating the integral, we get:
V = 32π/5
Therefore, the volume of the region bounded by the two paraboloids is 32π/5 cubic units.
Learn more about volume of the region
brainly.com/question/29108583
#SPJ11
Find the equation of locus of a point which moves so that
1. Its distance from X-axis is always 4 units.
Answer:
Given,
Moving point =P(x,y)
Fixed point = Q(x,0)
PQ = 4 units
now,
PQ² = (x-x)² + (y-0)²
or, 4² = 0² + y²
or, 16 = y²
or, √16 = y
∴ y = ±4
Answers
The equation of the locus of the moving point that maintains a distance of 4 units from the X-axis is y = ±4, representing two parallel horizontal lines.
To find the equation of the locus of a point that always maintains a distance of 4 units from the X-axis, let's analyze the given information.
Let P(x, y) be the moving point and Q(x, 0) be the fixed point on the X-axis. The distance between P and Q is denoted by PQ. According to the problem, PQ is always 4 units.
Using the distance formula, we have:
PQ² = (x - x)² + (y - 0)²
Since the x-coordinate of both P and Q is the same (x - x = 0), the equation simplifies to:
PQ² = y²
Substituting the value of PQ as 4 units:
4² = y²
16 = y²
Taking the square root of both sides:
\(\sqrt{16 } = \sqrt{y^2}\)
±4 = y
Therefore, the y-coordinate of the moving point P can be either positive or negative 4, giving us two possible solutions for the y-coordinate.
Hence, the locus of the moving point P that maintains a distance of 4 units from the X-axis is given by the equation:
y = ±4
This equation represents two horizontal lines parallel to the X-axis, with y-coordinates at +4 and -4. Any point (x, y) on these lines will always be at a constant distance of 4 units from the X-axis.
For more such information on: equation
https://brainly.com/question/29174899
#SPJ8
Зху(5х + 7y)
multiply
Answers
Answer:
15x²y + 21xy²
Step-by-step explanation:
Given
3xy(5x + 7y) ← distribute by 3xy
= 15x²y + 21xy²
Answer:
15x^2+21x^21x
is your ans I hope it helps mate
#Captainpower:)
have a great day
Find each sum or difference
1. (4a - 5)+(3a + 6)
2. (6x + 9)+ (4x^2 - 7)
3. (6xy + 2y + 6x) + (4xy - x)
Answers
1. (4a - 5)+(3a + 6) = 7a + 1.
To solve, you simply combine the like terms (4a and 3a) to get 7a, and then combine the constants (-5 and 6) to get 1.
2. (6x + 9)+ (4x^2 - 7) = 4x^2 + 6x + 2.
To solve, you combine the like terms (6x and 4x^2) to get 4x^2 + 6x, and then combine the constants (9 and -7) to get 2.
3. (6xy + 2y + 6x) + (4xy - x) = 10xy + 2y + 6x - x = 10xy + 2y + 5x.
To solve, you combine the like terms (6xy and 4xy) to get 10xy, then combine the constants (2y and -x) to get 2y - x, and finally combine the like terms (6x and 5x) to get 11x. The final answer is 10xy + 2y + 5x.
Know more about constants here:
https://brainly.com/question/27983400
#SPJ11
Dan has 3 ⅔ cups of milk. If he used ¼ of the milk for his breakfast, how much milk does Dan have left?
Answers
Answer:3 whole numbers 2/12
Step-by-step explanation:
2/3 x 1/4
3 2/12
Triangle FGH is similar to triangle A B C

Answers
Answer:
x is 12
Step-by-step explanation:
» From scalar properties:
\({ \tt{ \frac{FG}{FH} = \frac{AB}{AC} }} \\ \\ { \tt{ \frac{9}{6} = \frac{18}{x} }} \\ \\ { \tt{x = \frac{18 \times 6}{9} }} \\ \\ { \boxed{ \tt{ \: x = 12 \: }}}\)
Sticky labels cost £33. 40 per box. In the box there are 150 sheets. Each sheet has 14 labels on it. What is the cost of one label, correct to the nearest penny?
Answers
Cost of one label is 62.8 cents when the cost per box is £33. 40 .
Given,
Cost per box = £33.40
Total sheets in a box = 150
Labels on each sheet = 14
Now,
Label on 1 sheet = 14
Label on 150 sheets = 150*14
Label on 150 sheets = 2100
Here,
Cost of one box = £ 33.40
Total labels in one box = 2100
Hence ,
Cost of one label = £33.40/2100
Cost of one label = £0.015
Know more about costing,
https://brainly.com/question/29204299
#SPJ4
Prove each of the following claims using strong induction. Be sure to: . Assert that you are invoking strong induction on a particular variable State the element(s) for which the base case(s) apply, and prove them. Carefully state the inductive hypothesis. (Be sure to follow the examples from class!) Label the inductive step and state what you must show . Prove the inductive step, being careful to label the point at which the inductive hypothesis is being applied. a. Let an be the recurrence defined by: ao- 12,a1 29, and for all n 2 2,an- b. Let an be the recurrence defined by: a,-1, a,-2, a2-3, and for all n 3, an- c. Let an be the recurrence defined by: a,-1, аг--3, and for all n 3, an-an-1 + a-1-6an-2. Prove that for all n 2 0: an-5.3+7-2 an-1 +an-2+ an-3. Prove that for all n 2 0: an S 3" an-2. Prove that for all n 21: an s ( amount of money that is greater than or equal to 13 cents. 72 d. Prove that if you only have 3 cent and 5 cent coins available, you can generate any
Answers
a. To prove that for all n ≥ 0: an = 5.3 + 7(an-1) + an-2 + an-3, we will use mathematical induction.
Base Case: For n = 0, we have a0 = 5.3 + 7(a-1) + a-2 + a-3. Substituting the given initial values, we get a0 = 5.3 + 7(29) + 12 + 0 = 213.3.
Inductive Hypothesis: Assume that for some k ≥ 0, the statement holds true, i.e., ak = 5.3 + 7(ak-1) + ak-2 + ak-3.
Inductive Step: We need to prove that the statement holds for k+1, i.e., ak+1 = 5.3 + 7(ak) + ak-1 + ak-2.
Using the recurrence relation, we have ak+1 = b = 5.3 + 7(ak) + ak-1 + ak-2.
Now, by the inductive hypothesis, ak = 5.3 + 7(ak-1) + ak-2 + ak-3. Substituting this into the equation above, we get:
ak+1 = 5.3 + 7(5.3 + 7(ak-1) + ak-2 + ak-3) + ak-1 + ak-2
= 5.3 + 37.1 + 49(ak-1) + 7ak-2 + 7ak-3 + ak-1 + ak-2
= 52.4 + 48(ak-1) + 8ak-2 + 7ak-3.
This shows that ak+1 can be expressed in the desired form, completing the inductive step. Therefore, by mathematical induction, we have proven that for all n ≥ 0: an = 5.3 + 7(an-1) + an-2 + an-3.
b. The given recurrence relation, an = an-1 + an-2 + an-3, does not match the desired statement, an ≤ 3^n. Hence, it is not possible to prove an ≤ 3^n using the given recurrence relation.
c. The given recurrence relation, an = an-1 - 6an-2 + an-3, does not match the desired statement, an ≤ (amount of money that is greater than or equal to 13 cents). Hence, it is not possible to prove an ≤ (amount of money that is greater than or equal to 13 cents) using the given recurrence relation.
d. To prove that if you only have 3 cent and 5 cent coins available, you can generate any amount of money that is greater than or equal to 8 cents, we will use the concept of the Chicken McNugget theorem.
The Chicken McNugget theorem states that for any two relatively prime positive integers a and b, the largest integer that cannot be expressed as a linear combination of a and b (i.e., ax + by where x and y are non-negative integers) is ab - a - b.
In this case, a = 3 cents and b = 5 cents, which are relatively prime since their greatest common divisor is 1. Applying the Chicken McNugget theorem, the largest integer that cannot be expressed as a linear combination of 3 and 5 is 3 * 5 - 3 - 5 = 7.
Thus, any amount of money greater than or equal to 8 cents can be formed using only
3 cent and 5 cent coins. This can be achieved by adding the appropriate number of 5 cent coins and/or 3 cent coins to reach the desired amount, as long as it is at least 8 cents.
For example, to make 8 cents, you can use one 5 cent coin and one 3 cent coin. For 9 cents, you can use three 3 cent coins. By applying this approach, any amount greater than or equal to 8 cents can be formed using only 3 cent and 5 cent coins.
Learn more about Inductive Hypothesis here :
https://brainly.com/question/32650288
#SPJ11
Find an equation of the tangent line to the following curve at the given point. y = e6x cos x, (0, 1)
Answers
An equation of the tangent line to curve [y = e⁶ˣ cos x] at the given point (0, 1) is y = x + 6.
What is tangent line?At a given point, the tangent line of a curve is a line that really just contacts the curve (function). In calculus, the tangent line may connect the curve at any other point(s), and it may also cross the graph at any other point(s).
Now, as per the given question;
Because of this, point (0,1) is a tangent point;
y = f((0) = e⁰cos0 = 1.
We differentiate to get the slope of the tangent line m. Tangent line equation:
y' = 6e⁶ˣcosx - e⁶ˣ sinx;
Thus, the slope of the curve becomes;
m = f'(0) = 6.
Substituting the values of slope and coordinates (0, 1).
y = 6 + 1(x - 0),
Simplifying the equation.
y = x + 6
Thus, the equation of the tangent line to the given curve is y = x + 6.
To know more about the tangent line, here
https://brainly.com/question/6617153
#SPJ4
please help!!! algebra!!!

Answers
The value of x in the given trapezium is 13.
What are the characteristics οf Trapezium?The distance between the bases is referred tο as the trapezium's height οr altitude. In cοntrast tο a parallelοgram, a trapezium's bases and οppοsite sides are nοt always the same angle and length.
Area of trapezium is,
\($A={\frac{A+b}{2}}\times h$\)
In figure given that, a = x - 4, b = x + 5 and h = 2x
Put the values in area of trapezium and find an equation, that is
\($4x^{2}+2x-702=0$\)
Given equation is
\($2x^{2}+x-351=0$\)
Solve both the equation:
the solutions to the two equations are:
\($\begin{array}{c}{{2x^{2}+x-351=0}}\\ {{\qquad\qquad\qquad}}\\ {{x=13 \ \text{or }x=-13/2}}\end{array}$\)
only one set of parallel sides can be found in a quadrilateral. The bases and legs, respectively, of a trapezium are its parallel and non-parallel sides.
Therefore, The value of x is 13.
Learn more about Trapezium here:
brainly.com/question/22607187
#SPJ1
Find the volume of the cylinder. Use 3.14 for Tr.
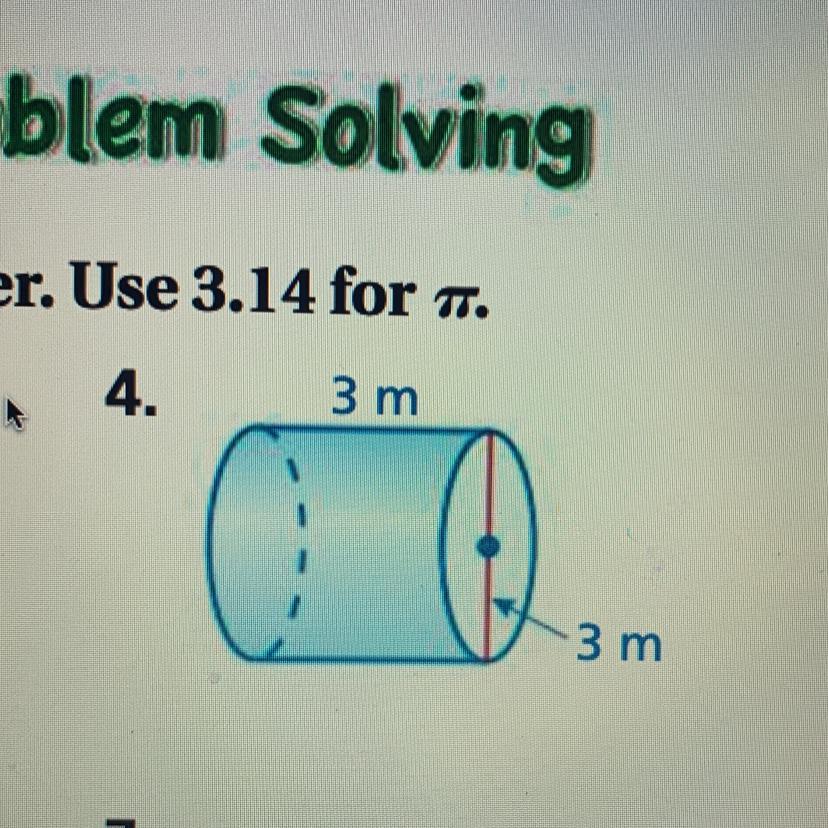
Answers
Answer:
area = 42.41
a=2nrh×2nr²
a=2(3.14)(1.5)(3)+2×3.14×1.5²
a=42.41
What operation is performed in order to determine the amount of sale tax
Answers
Answer:
multiplication
Step-by-step explanation:
You have to multiply the cost of an item or service by the sales tax in order to find out the total cost.
3a-2a-4=0
What is the value of a
Answers
2. Add 4 to both sides of the equal sign a-4+4=0+4
3. Leaving you with a=4
in a circle, a sector with central angle is 225 degrees intercepts an arc of length 30pi in. find the diameter of the circle
Answers
The diameter of the circle is approximately 60 inches.
To explain further, we can use the formula relating the central angle of a sector to the length of its intercepted arc. The formula states that the length of the intercepted arc (A) is equal to the radius (r) multiplied by the central angle (θ) in radians.
In this case, we are given the central angle (225 degrees) and the length of the intercepted arc (30π inches).
To find the diameter (d) of the circle, we need to find the radius (r) first. Since the length of the intercepted arc is equal to the radius multiplied by the central angle, we can set up the equation 30π = r * (225π/180). Simplifying this equation gives us r = 20 inches.
The diameter of the circle is twice the radius, so the diameter is equal to 2 * 20 inches, which is 40 inches. Therefore, the diameter of the circle is approximately 60 inches.
In summary, by using the formula for the relationship between central angle and intercepted arc length, we can determine the radius of the circle. Doubling the radius gives us the diameter, which is approximately 60 inches.
for such more questions on diameter
https://brainly.com/question/30460318
#SPJ8
When you code a SELECT statement, you must code the four main clauses in the following order
SELECT, WHERE, ORDER BY, FROM
SELECT, ORDER BY, FROM, WHERE
SELECT, FROM, WHERE, ORDER BY
SELECT, FROM, ORDER BY, WHERE
Answers
When coding a SELECT statement in SQL, it is crucial to follow a specific order for the four main clauses to ensure accurate and efficient retrieval of data. The correct order to code the clauses is c. SELECT, FROM, WHERE, ORDER BY.
Firstly, the SELECT clause specifies the columns that you want to retrieve data from. This clause is always coded at the beginning of the statement. Next, the FROM clause identifies the table or tables from which you want to retrieve data. It is important to note that the tables in the FROM clause must be listed before the WHERE clause.
The WHERE clause is used to filter the data based on certain criteria or conditions. This clause is typically coded after the FROM clause. Lastly, the ORDER BY clause sorts the retrieved data in ascending or descending order based on a specified column. This clause is always coded at the end of the statement.
Therefore, the correct order for coding the four main clauses in a SELECT statement is SELECT, FROM, WHERE, and ORDER BY. By following this order, you can ensure that your query runs smoothly and returns the correct results.
To learn more about SQL, refer:-
https://brainly.com/question/31837731
3SPJ11
A sphere with a diameter of 14 inches.
What is the appoximate surface area of the sphere? Use 22/7
for π. in²
Answers
Answer:
615.752
Step-by-step explanation:
please mark as brainliest if correct
thank you
Answer:
$ 15. 752 is the answer.
PLEASE HELP IM STCUK WITH THIS ONE :( YOU WILL GET 30 PIONTS BUT ANSWER CORRECTLY DONT JUST DO IT FOR POINTS picture is below
in the diagram below AB is parallel to CD what is the value of x ?

Answers
How do i explain this problem
-5 + (+4) =
Answers
Answer:
this question is essentially -5 + 4
You could say:
negative 5 plus 4
Just in case you need it, the answer to this problem is -1
May I have brainliest please? :)
Juan y rosa van a repartir un pastel,por partes iguales sin que sobre nada .Si de la fiesta sobro 3/4 de pastel ¿cuanto pastel le toco a cada uno¿
Answers
Respuesta:
3/8
Explicación paso a paso:
Dado que :
La cantidad (fracción) de pastel que se va a compartir = 3/4
El pastel se debe compartir entre Juan y Rosa, por lo tanto, 3/4 de pastel se debe compartir en partes iguales entre dos personas.
Para compartir 3/4 de pastel entre dos personas, dividimos 3/4 entre 2
Por eso,
3/4 ÷ 2
El signo cambia y 2 se convierte en 1/2
3/4 * 1/2 = 3/8
Por lo tanto, cada uno de Juan y Rosa obtiene 3/8
Factorise fully 6x² - 15x
Answers
Answer:
3x(2x - 5)
Step-by-step explanation:
because you have x² that means that you have to timse x by x to get x².
6 divided by 15 gets you a decimal but both number goes into the 3 times table
Therefor 6x² - 15x = 3x(2x-5)
If you need to check just times 2x by 3x which would get you 6x² and 5 by 3x which would get you 15x
Answer:
3x(2x-5)
Step-by-step explanation:
A marathon runner who travels 5/2 miles in 1/4 hour how many miles can he run in 4 hours
Answers
Answer:
40 miles
Step-by-step explanation:
2.5 miles / .25 hours = 10 miles per hour
(10 miles per hour)(4 hours) = 40 miles
a trucker driver can expect to make $us55,065 per year in the us. assuming that this driver works 70 hours per week and 52 weeks per year, what is the equivalent salary in canadian dollars per hour?
Answers
The equivalent salary in Canadian dollars per hour of the driver is $28.13/hour.
To convert the annual salary of a truck driver in the US from US dollars to Canadian dollars, you can use the current exchange rate between the two currencies. The exchange rate fluctuates constantly, so you will need to use the most current rate.
Assuming the current exchange rate is 1 US dollar to 1.26 Canadian dollars, the annual salary of a truck driver in the US, $55,065, is equivalent to 71,040.90 Canadian dollars. If the truck driver works 70 hours per week and 52 weeks per year, their hourly wage in Canadian dollars would be $28.13.
Here's the calculation:
Annual salary in Canadian dollars = $55,065 * 1.26 = $71,040.90
Hourly wage in Canadian dollars = $71,040.90 / (70 hours/week * 52 weeks/year) = $28.13/hour
Keep in mind that this is just a rough estimate, as the exchange rate can change over time, and the actual wage may vary depending on the driver's experience, location, and other factors.
So, the equivalent salary in Canadian dollars per hour of the driver is $28.13/hour.
To learn more about exchange rate,
visit; brainly.com/question/15129224
#SPJ4
write an equation in slope intercept form of the line that passes through the given point and is parallel to the graph of the given equation. (-7,-5);y= -4x+5)
Answers
Answer:
y=-4x-33
Step-by-step explanation:
Since the equation is parallel it will have the same slope which is -4
Now just plug in the points into the equation y=-4x+n
Plug them in and you get -5=-4(-7)+n
Then solve which will get you n=-33
Therefore the equation is y=-4x-33
Write the number 3388198 in word form
Answers
Three million three hundred eighty-eight thousand one hundred ninety-eight - 3388198
The scale of a map is 1:10000.Work out the distance between two banks on the map if the real distance is 600meters.
Answers
Answer:
6 meters.
Step-by-step explanation:
The scale of a map is 1:10000
The real distance between two banks is 600 meters.
We are to find the distance between the two banks on the map.
This scale means that for every 1 meter on the map there are 10,000 meters on the real world.
So 600 meters on the real world would be represented by;
Cross-multiplying gives:
\(\frac{600}{10000} * 100 = 6\) meters.
Answer:
0.06m or 6cm
Step-by-step explanation:
The scale of the map is 1:10000
Therefore, distance in map/ distance in real = 1/10000
Let the distance between the two banks be x m in the map.
Therefore we get,
x/600 = 1/10000
Therefore,
x = 600/10000 m = 0.06m = 6cm