Which expression is the simplest form of 5(2x - 3) - 3(x + 4) / 9
A. 7x - 3
B. 7x - 27/9
C. 7x - 3
D. 13x - 27/9
Answers
Answer:
The answer is B.
Step-by-step explanation:

The simplified expression is 7x - 27/9
What is expression?Expressions in math are mathematical statements that have a minimum of two terms containing numbers or variables, or both, connected by an operator in between. The mathematical operators can be of addition, subtraction, multiplication, or division. For example, x + y is an expression, where x and y are terms having an addition operator in between. In math, there are two types of expressions, numerical expressions - that contain only numbers; and algebraic expressions- that contain both numbers and variables.
An expression is a combination of terms that are combined by using mathematical operations such as subtraction, addition, multiplication, and division. The terms involved in an expression in math are:
Constant: A constant is a fixed numerical value.Variable: A variable is a symbol that doesn't have a fixed value.Term: A term can be a single constant, a single variable, or a combination of a variable and a constant combined with multiplication or division.Coefficient: A coefficient is a number that is multiplied by a variable in an expression.Given:
5(2x - 3) - 3(x + 4) / 9
=10x-15-3x-12/9
=10x-3x-15-12/9
=7x-27/9
Learn more about expression here:
https://brainly.com/question/14083225
#SPJ5
Related Questions
(9+2).0 = 0
Is it commutative, associative, identity ,inverse, property of zero, distributive
Answers
Answer:
The property used will be property of zero.
Step-by-step explanation:
If an equation or expression ever equals zero, then it will be property of zero.
I need help on question c and d

Answers
Answer:
c. 4^3 * 5^2 (1600)
d. 9^4 * 7^2 (321489)
Step-by-step explanation:
Hi!
Remember that exponents are the number times itself (2*2 = 2^2).
So, in c, we have 4 times 4 times 4. We have 4 multiplied by 4 3 times. We can also write this as 4^3.
We also have 5 times 5. We can also write this as 5^2.
However, we need to multiply 5^2 by 4^3. So:
4^3 times 5^2 or 1600.
d.
Let's group the similar numbers together.
9 x 9 x 9 x 9 and 7 x 7
There are 4 9's, so 9^4.
There are 2 7's, so 7^2
Multiply the 2.
9^4 * 7^2
please help need answer fast please

Answers
Answer: 208.2 in
Step-by-step explanation: I'm am super smart
Hope this helps : D
y=6x-11
-2x-3y=-7
find the solution
Answers
Answer:
x = 13/8
y = 5/4
Step-by-step explanation:
y = 6x - 11
-2x - 3y = -7
6x - y = 11
-2x - 3y = -7
18x - 3y = 33
-2x - 3y = -7
16x = 26
x = 26/16 = 13/8
y = 39/4 - 11 = 5/4
y=6x-11
-2x-3y=-7
The solution to the system of equations is:
5/4

Please its really urgent, step by step working out
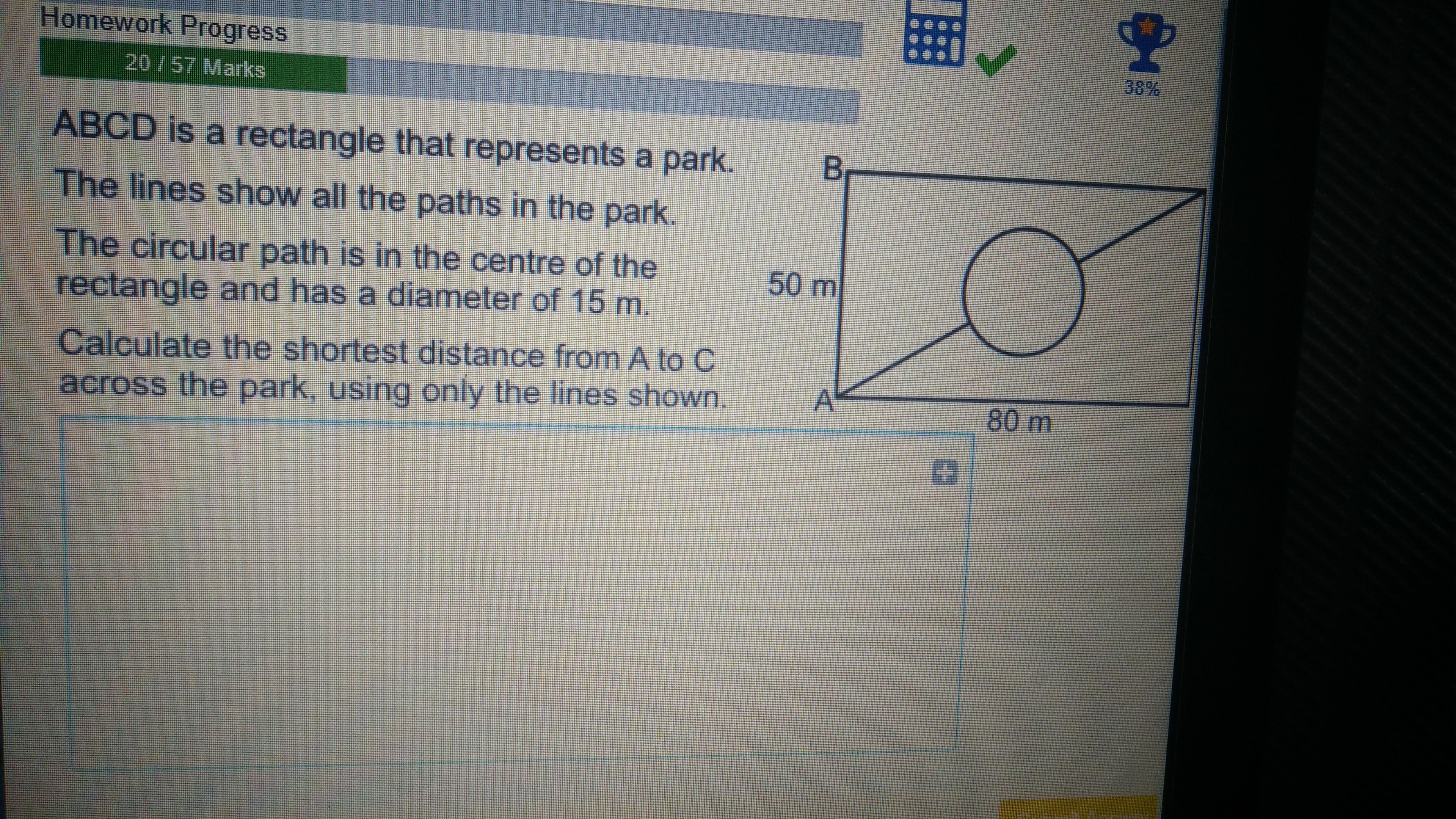
Answers
Answer:
70.99
Step-by-step explanation:
Use Pythagorean Theorem to find the shortest distance.
80^2-50^2=3900
Square rt= 62.44
Subtract by 15
47.44
Next find half of the circular path it is (3.14 x 15)/2
23.55
Add 47.44+23.55=70.99
Hope this is correct
B is the midpoint of AC. AB = 2x - 3, and AC = 5x - 11. Solve for BC.
Answers
Answer:
it all =22
Step-by-step explanation:
How many solutions are there to the equation below?
= 7

Answers
Answer:
b. 1
Step-by-step explanation:
there is only one solution because:
√49= 7
or
7²= 49
Isaac applied the steps below to find the product of (4.2)(-5.4).
.
Step 1: (4.2)(-5.4) = (-5.4)(4.2)
Step 2:
= (-5.4)(4) + (-5.4)(0.2)
Step 3:
= (-21.6) + (-1.08)
Step 4:
=-22.68
Which step shows where Isaac applied the distributive property?
Step 1
0 0
Step 2
Step 3
Step 4
Answers
The answer is step 2. hope it helps.
Answer:
step 2
Step-by-step explanation:
Select the graphs that show a proportional relationship between x and y
Answers
The total cost of bus tickets from karachi to hyderabad for 2 adults and 4 children was rs 4940.eac child cost rs 520 less than an adult ticket what was the cost of an adult ticket?
Answers
The cost of an adult ticket is Rs 1170 using equations.
What is an equation?A mathematical statement known as an equation shows the equality of two mathematical expressions.
Mathematical algebraic equations typically have one or more variables.
Let the cost of an adult ticket be x.
Given that each child costs Rs 520 less than an adult ticket.
Then, the cost of a child ticket = x - 520.
The total cost of bus tickets for 2 adults and 4 children = Rs 4940
So,
2x + 4(x-520) = 4940
⇒2x + 4x - 2080 = 4940
⇒6x = 7020
⇒x = 1170
Therefore, the cost of adult ticket is Rs 1170.
To learn more about equations, visit:
https://brainly.com/question/23579483
#SPJ4
n identical balls are thrown into 10 bins numbered 1 through 10. (If it helps think n is large compared to 10.) A configuration is specified by how many balls land into bin #1, bin #2, and so on. So two configurations are distinct if the number of balls in any particular bin differ in them. For how many configurations do we have that each bin is nonempty?
Answers
The final answer is:
10^n - 9^n + 10 choose 2 * 8^n - 10 choose 3 * 7^n + 10 choose 4 * 6^n - 10 choose 5 * 5^n + 10 choose 6 * 4^n - 10 choose 7 * 3^n + 10 choose 8 * 2^n - 10 choose 9 * 1^n
To find the number of configurations where each bin is nonempty, we can use the principle of inclusion-exclusion.
First, let's find the total number of configurations. We have n identical balls that can go into 10 different bins, so the total number of configurations is:
10^n
Now, let's find the number of configurations where at least one bin is empty. We can do this by considering the number of ways to distribute the n balls into 9 bins (since we cannot have an empty bin), and then subtracting that from the total number of configurations. The number of ways to distribute n balls into 9 bins is:
9^n
So the number of configurations where at least one bin is empty is:
10^n - 9^n
However, we have overcounted the configurations where two bins are empty (since we subtracted them twice). To correct for this, we need to add back in the number of configurations where two bins are empty.
We can do this by considering the number of ways to distribute the n balls into 8 bins (since we cannot have two empty bins), and then multiplying that by the number of ways to choose two bins out of 10 to be empty:
10 choose 2 * 8^n
So the number of configurations where at least two bins are empty is:
10 choose 2 * 8^n
But now we have undercounted the configurations where three bins are empty (since we added them back in twice). To correct for this, we need to subtract out the number of configurations where three bins are empty. We can do this by considering the number of ways to distribute the n balls into 7 bins (since we cannot have three empty bins), and then multiplying that by the number of ways to choose three bins out of 10 to be empty:
10 choose 3 * 7^n
Continuing with this process, we can find the number of configurations where four bins are empty, five bins are empty, and so on. The final answer is:
10^n - 9^n + 10 choose 2 * 8^n - 10 choose 3 * 7^n + 10 choose 4 * 6^n - 10 choose 5 * 5^n + 10 choose 6 * 4^n - 10 choose 7 * 3^n + 10 choose 8 * 2^n - 10 choose 9 * 1^n
This expression gives us the number of configurations where each bin is nonempty.
To know more about nonempty refer here
https://brainly.com/question/30888819#
#SPJ11
8. Separate 84 into two parts such that one part will be 12 less than twice
the other.
Answers
Answer:
x + (2x-12) = 84
x = 32
Step-by-step explanation:
you can say (part 1) + (part 2) = 84
one part is x (a variable) and
other part is 12 less than twice the other: when it says "12 less" is " - 12" and twice of part one 2x, you can say (2x - 12)
(part 1) + (part 2) = 84
x + (2x-12) = 84
3x - 12 = 84
3x = 96
x = 32
(part 1) + (part 2) = 84
(32) + (2*32 - 12) = 84
(32) + (52) = 84
Ayuden por favor, no entiendo este problema

Answers
We will get that the angle theta is:
θ = β/2
How to find the value of theta?Remember that the sum of the interior angles of any triangle must be equal to 180°.
Now, looking at the triangle in the left, we can see that the top angle is equal to:
180 - 2α
The right angle is equal to:
180 - 2β
And the left angle is α
Then we can write:
α + (180 - 2α) + (180 - 2β) = 180
-α - 2β = -180
α = 180 - 2β
Now we can go to the other triangle, where theta is, and write:
α + β + 2θ = 180
Replacing what we found above, we get:
180 - 2β + β + 2θ = 180
-β + 2θ = 0
θ = β/2
That is the best simplification we can get with the given diagram.
Learn more about interior angles at:
https://brainly.com/question/24966296
#SPJ1
5) A tortoise's fastest rate of travel is 225 feet in 15 minutes. Write
this rate as a Unit Rate.
Answers
Or
900 ft/1 hour
Answer:
900 feet per hour
Step-by-step explanation:
225×4 = 900
15×4=60
the tortoise's rate of speed is 900 feet per hour
hope that helps.
What three-dimensional figure is formed when the triangle shown is rotated around the dashed line?
A. cone
B. cylinder
C. double cone
D. hemisphere

Answers
Answer: C
Step-by-step explanation: after rotating, if you split it in half horizontally, you have two cones
The three-dimensional figure formed when the triangle is rotated around the dashed line through B and C is a cone.
What is a cone?A cone is a three-dimensional geometric form with a flat base and a smooth, tapering apex or vertex. A cone is made up of a collection of line segments, half-lines, or lines that link the base's points to the apex, which is a common point on a plane that does not include the base.
When we rotate a two-dimensional shape around an axis, we create a three-dimensional solid. This process is known as "revolution" or "rotational symmetry".
In this particular case, we have a triangle that can be rotated around the line segment that connects points B and C. If we were to rotate the triangle around this axis, we would create a three-dimensional solid. To figure out what kind of solid this is, we can think about the cross-sections that would be created if we were to slice through the solid perpendicular to the axis of rotation.
If we were to slice through the solid perpendicular to the axis of rotation, we would get a circle. This means that the solid created by rotating the triangle is a cylinder.
To learn more about the cone;
brainly.com/question/16394302
#SPJ2
Determine the seating capacity of an auditorium with 37 rows of seats if there are 16 seats in the first row, 21 seats in the second row, 26 seats in the third row, and so on. 693 Incorrect: Your answer is incorrect. seats
Answers
The seating capacity of an auditorium with 37 rows of seats is 23,271.
Given that the first row has 16 seats, the second row has 21 seats, the third row has 26 seats, and so on up to the 37th row. Using the formula for the sum of an arithmetic series, we have: Sn = n/2[2a + (n - 1)d] where n is the number of terms in the series a is the first term of the series d is the common difference of the series.
Here, a = 16, d = 5, and n = 37. Plugging in these values in the formula, we get Sn = 37/2[2(16) + (37 - 1)5]Sn = 37/2[32 + 180]Sn = 37/2(212)Sn = 23,271. Therefore, the seating capacity of the auditorium is 23,271.
Learn more about arithmetic series here:
https://brainly.com/question/16415816
#SPJ11
There are 14 dogs at the dog park on a busy Saturday. 2 of them are springer spaniels.
What is the probability that a randomly selected dog is a springer spaniel?
Write your answer as a fraction or whole number.
Answers
Answer:1/7
Step-by-step explanation: You take the amount that are springer spaniels and you put them with the whole of the dogs in the park 14 so you would have 2/14. You can reduce this fraction to 1/7 by dividing both the top and bottom of the fraction by 2.
In a popular online role playing game, players can create detailed designs for their character's "costumes," or appearance. Pedro sets up a website where players can buy and sell these costumes online. Information about the number of people who visited the website and the number of costumes purchased in a single day is listed below. 178 visitors purchased no costume. 165 visitors purchased exactly one costume. 21 visitors purchased more than one costume. Based on these results, express the probability that the next person will purchase no more than one costume as a decimal to the nearest hundredth.
Answers
Answer:
Step-by-step explanation:
21
Please help ASAP! Fake answers will be reported.
What is the resulting equation when the expression for y in the second equation is substituted into the first equation?
3x + y = 1
y = 3 - 4x
Answers
Answer:
-x + 6 = 1 is the resulting equation when the expression for y in the second equation is substituted into the first equation 3x + y = 1 y = 6 - 4x . 5x = 10 is the result of adding the system of equations: 2x + y = 4 3x - y = 6 .Step-by-step explanation:
mark brainiest
Answer:
the ans is -5 hope it may help u
Step-by-step explanation:
first 3x +y =1
y = -3x +1
putting the value of y in other equation
y=3-4x
-3x+1 = 3 -4x
x = 2 putting the value of x in first equation
6 + y =1
so y =-5
The utility industry had 639.5 thousand jobs in 2010 and is expected to decline at an average rate of 2.6 thousand jobs per year from 2010 to 2020. Assuming this holds true, what will be the utility’s percent change from 2010 to 2020
Answers
The utility’s percent change from 2010 to 2020 is a decrease of 4.07%
How many years are between 2010 and 2020?
There are 10 years in between 2010 and the year 2020, which means that the total decline over a period of 10 years is the annual decrease multiplied by 10.
Total decrease in 10 years=2.6*10
Total decrease in 10 years=26.0
Utility industry jobs in 2020=639.5-26.0
Utility industry jobs in 2020=613.5
The percentage change 2010-2020=(2020 jobs/2010 jobs)-1
The percentage change 2010-2020=(613.5/639.5)-1
The percentage change 2010-2020=-4.07%
Find out more about percentage change on:https://brainly.com/question/17308462
#SPJ1
If an arrow is shot straight upward on the moon with a velocity of 74( m)/(s), its height (in meters ) after t seconds is given by s(t) = 74t -0.83t^(2). What is the velocity of the arrow (include units ) after 10 seconds?
Answers
The velocity of the arrow after 10 seconds is 57.4 meters per second (m/s). The velocity of the arrow after 10 seconds, we need to take the derivative of the height function, s(t), with respect to time, t. The derivative of s(t) is given by:
s'(t) = 74 - 1.66t
The velocity of the arrow changes over time. To find the velocity after 10 seconds, we can simply plug in t = 10:
s'(10) = 74 - 1.66(10)
s'(10) = 57.4
The velocity of the arrow after 10 seconds is 57.4 m/s.
The units for the velocity are meters per second, which is the same as the units for the initial velocity of the arrow given in the problem. This makes sense, as the arrow is only subject to the gravitational force of the moon, which is constant.
The acceleration due to gravity is constant, and the velocity of the arrow will decrease at a constant rate over time.
The velocity of the arrow after 10 seconds can be found by taking the derivative of the height function with respect to time, which gives us the velocity function:
v(t) = ds/dt = 74 - 1.66t
To find the velocity after 10 seconds, plug in t=10:
v(10) = 74 - 1.66(10) = 74 - 16.6 = 57.4 m/s
To know more about velocity visit:-
https://brainly.com/question/29253175
#SPJ11
Solve the inequality.
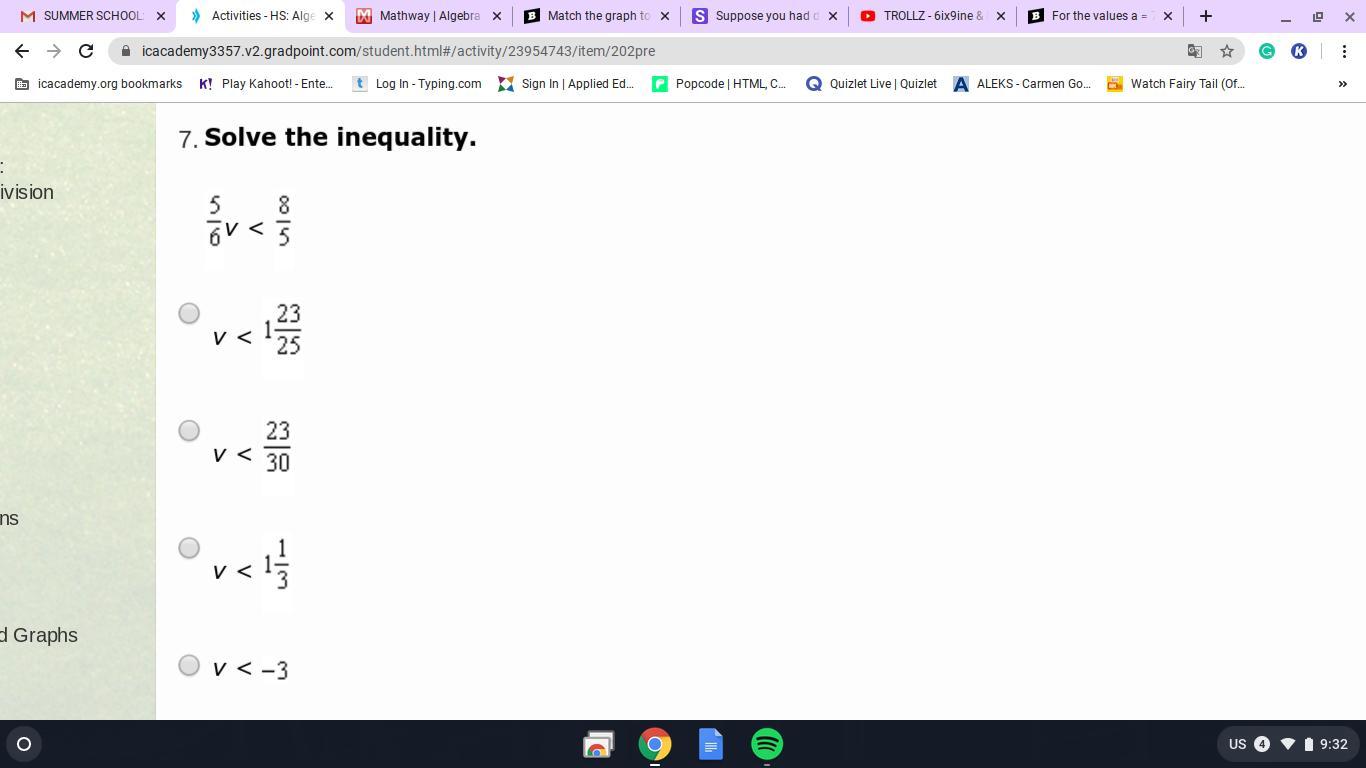
Answers
Answer:
the first one, v < 1 23/25
Step-by-step explanation:
multiply both sides by 6 and divide by 5
v < 48/25, or v < 1 23/25
Answer:
v < 1 23/25
Step-by-step explanation:
5/6 v < 8/5
Multiply each side by 6/5
6/5*5/6 v < 8/5*6/5
v < 48/25
Rewrite as a mixed number
v < 1 23/25
The length of a rectangle i 2cm greater than the width of the rectangle. The perimeter of the rectangle i 24cm
Answers
The length of the rectangle is 7 cm and the width is 5 cm.
Perimeter of a rectangle:The whole distance covered by the rectangle's borders or its sides is known as its perimeter. As we know the rectangle will have 4 sides then the perimeter of the rectangle will be equal to the total of its four sides. And the unit will be in meters, centimeters, inches, feet, etc.
The formula for the Perimeter of the rectangle is given by
Perimeter = 2( Length + Width )Here we have
The length of a rectangle is 2cm greater than the width of the rectangle
And perimeter of the rectangle = 24 cm
Let x be the width of the rectangle
From the given data,
Length of the rectangle = (x + 2) cm
As we know Perimeter of rectangle = 2(Length+width)
=> Perimeter of rectangle = 2(x+2 + x) = 2(2x +2)
From the given data,
Perimeter of rectangle = 24cm
=> 2(2x +2) = 24 cm
=> (2x +2) = 12 [ Divided by 2 into both sides ]
=> 2x = 12 - 2
=> 2x = 10
=> x = 5 [ divided by 2 into both sides ]
Length of rectangle, (x+2) = 5 + 2 = 7 cm
Therefore,
The length of the rectangle is 7 cm and the width is 5 cm.
Learn more about Perimeter of a rectangle at
https://brainly.com/question/29595517
#SPJ4
Check here LOADING... for instructional material to complete this problem.
Evaluate the formula z=
p−p
pq
n when p=
388
1386, n=1386, p=0.30, and q=1−p

Answers
Answer:
-1.63
Step-by-step explanation:
Plug in the values listed into the equation
([388/1386] - 0.30) / √(0.30[1-0.30)/1386
-0.02006/0.01231
-1.63
Someone plz help me giving brainliest (and yes this question is together)

Answers
Baseball doughnuts are weights placed on baseball bats during warmup. A high school team uses baseball doughnuts that weigh 5 ⅐ ounces each. The team brings 8 baseball doughnuts to away games. What is the total weight of the baseball doughnuts?
Part A: 5 1/7 x 8
Part B: 36/7 x 8/1 = 288/7
Sry i.d.k C
Step-by-step explanation:

What is the value of x (8x-8)° (7x+8)°
Answers
I'm going to assume they are the same angle.
Steps to solve:
(8x - 8) = (7x + 8)
~Add 8 to both sides
8x = 7x + 16
~Subtract 7x to both sides
x = 16
Best of Luck!
The parent teacher association is raising money for a new swing set. They need $682.56 to purchase the swing set and receive a $200.00 donation. The remaining amount will be equally divided among 8 different student groups to raise. How much money will each student group need to raise in order to purchase the swing set?
Answers
Answer:
Each student will raise $60.32
Step-by-step explanation:
682.56-200.000 = 482.56
482.56/8 = $60.32
A dynamic cart is released from rest at the top of a 1. 5 meter long incline plane. Using photo-gate timers, the time to reach the bottom of the inclined plane is found to be 2. 231 seconds. What was the initial speed of the dynamic cart?
Answers
The dynamic cart is released from rest at the top of a 1.5-meter-long incline plane, and using photo-gate timers, the time to reach the bottom of the inclined plane is found to be 2.231 seconds. We will calculate the initial speed of the dynamic cart using this information.
According to the problem statement, we can state that the dynamic cart is released from rest at the top of the incline plane. This means that its initial velocity is zero. However, as it falls under the influence of gravity, its velocity increases. Let v be the velocity of the cart at the bottom of the incline plane, m be the mass of the cart, g be the acceleration due to gravity, h be the height of the incline plane, and θ be the angle between the incline plane and the horizontal.
The potential energy of the cart when it is at rest at the top of the incline plane ismghThe kinetic energy of the cart when it reaches the bottom of the incline plane is (1/2)mv2According to the law of conservation of energy, the total energy of the system remains constant.Equating the initial potential energy to the final kinetic energy, we getmgh = (1/2)mv2Hence,v = (2gh)^(1/2)But we know that h = 1.5 meters, g = 9.8 m/s2 (acceleration due to gravity), and θ = 0° (because the incline plane is horizontal). Therefore,v = (2 x 9.8 x 1.5)^(1/2)v = 6.132 m/sTherefore, the initial speed of the dynamic cart is 6.132 m/s.
To know more about inclined visit:
brainly.com/question/29360090
#SPJ11
Find the exact value for csc225°
Answers
Answer:
\(-\sqrt2\)
Step-by-step explanation:
csc 225 degrees is the multiplicative inverse of sin 225 degrees. sin 225 degrees. We can use a unit circle with radius of 1 to find out sin 225 degrees. a 225 degree rotation counter clockwise is equivalent to a 180 degree turn followed by a 45 degree turn. Therefore, the final value is going to be in the third quadrant, a 45 degree turn in. This means that sin(225 degrees) = \(-\sqrt2/2\) The multiplicative inverse of that is \(-\sqrt2\)
on a piece of paper graph y+45 ;*- 2. Then determine which answer
choice matches the graph you Drew.

Answers
Answer:its Graph C
(According to the law of Nicoloas Sadi Carnot)