Which math expression means "52 more than an unknown number"?
A. x + 52
B. X÷52
C. 52.x
D. x - 52
← PREVIOUS
SUBMIT

Answers
As per the statement in the question, the expression will be x + 52.
What are arithmetic operations?The four basic operations of arithmetic can be used to add, subtract, multiply, or divide two or even more quantities.
They cover topics like the study of integers and the order of operations, which are relevant to all other areas of mathematics including algebra, data processing, and geometry.
As per given information in the question,
Let the unknown number is x.
The statement says that the number is more than 52.
Then, the expression according to the statement will be,
= x + 52
To know more about arithmetic operations:
https://brainly.com/question/13585407
#SPJ1
Related Questions
Mr. Hooper has a tree in his front yard that grows every year. If the tree was 3 feet tall when he planted it 6 years ago , what is the current height of the tree in terms of f?
A. 3f + 6 feet
B. 6f + 3 feet
C. 3f + 18 feet
D. 6f + 18 feet
Answers
The height of the tree after 6 years can be expressed as "3 feet + 6f feet."
The correct answer is A. 3f + 6 feet.
To determine the current height of the tree in terms of "f,"
let's analyze the given information.
We know that the tree was initially 3 feet tall when it was planted 6 years ago.
Since the tree grows every year, we can assume that its growth rate is consistent.
Let's denote the current height of the tree as "h" (in feet).
After 6 years, the tree has grown by a certain amount, which we'll represent as "6f" (6 years multiplied by the growth rate "f").
Therefore, the height of the tree after 6 years can be expressed as "3 feet + 6f feet."
For similar question on height.
https://brainly.com/question/28122539
#SPJ8
The area of the circular base of a cone is 16π cm², and the slant height of the cone is 4 times the radius of the cone.
What is the approximate lateral area of the cone?
Answers
The approximate lateral area of the cone is equal to 200.96 cm².
How to calculate the lateral area of the cone?Mathematically, the lateral area of a cone can be calculated by using this mathematical expression:
Lateral surface area of a cone, LSA = πrl or πr√(r^2 + h^2)
Where
l represents the slant height of the cone.r represents the radius of the cone.h represents the height of the cone.How to calculate the area of a circle?Mathematically, the area of a circle can be calculated by using this formula:
Area of a circular base = πr²
16π = πr²
Radius, r = √16
Radius, r = 4 cm.
Substituting the given parameters into the lateral area of a cone formula, we have the following;
Lateral surface area of a cone, LSA = πrl = πr4(r)
Lateral surface area of a cone, LSA = 3.14 × 4 × 16
Lateral surface area of a cone, LSA = 200.96 cm².
Read more on surface area here: https://brainly.com/question/27812847
#SPJ1
Answer:
201 beause you are rounding to the nearest whole number
Step-by-step explanation:
Can u please help me with 3&4 I’m giving 20 point please help me

Answers
Answer:
Step-by-step explanation:

if z=-1-v3i and 26 = a +bi, then a =
and =

Answers
- Adult male Florida panthers have an
average weight of 52.6 kg. What is the
average weight of a male Florida panther
rounded to the nearest whole number?
Answers
The average weight of a male Florida panther rounded to the nearest whole number is 53 kg
What is average?
The middle number, which is determined by dividing the sum of all the numbers by the total number of numbers, is the average value in mathematics. When determining the average for a set of data, we add up all the values and divide this sum by the total number of values.
Average weight = 52.6 kg
52.6
The number after decimal point is 6 which is more than 5.
So add 1 to the 52, we get 53
Thus, the average weight of a male Florida panther rounded to the nearest whole number is 53 kg
To learn more about the average from the given link
https://brainly.com/question/1136789
#SPJ1
HELPPPP please!!!!!! im very confused i dont get the question. ( ILL GIVE BRAINILEST IF CORRECT)

Answers
The volume of the rectangular prism is 5 inches cube.
How to find the volume of a rectangular prism?A rectangular prism is a three-dimensional shape or figure. Therefore, the volume of a rectangular prism can be represented as follows:
volume of a rectangular prism = lwh
where
l = lengthw = widthh = heightTherefore,
l = 2 1 / 2 inches = 5 /2 inches
w = 1 inches
h = 2 inches
Hence,
volume of the rectangular prism = 5 / 2 × 1 × 2
volume of the rectangular prism = 10 / 2
volume of the rectangular prism = 5 inches cube
learn more on rectangular prism here: https://brainly.com/question/21308574
#SPJ1
Answer:It is 30 cubic inches.
Step-by-step explanation:
60. take as much time as you need to solve a and b :)

Answers
Given:
The given function is y
\(y=x^3-4x^2+2x-1\)Find:
we have to find the equation of tangent line to the given curve at a = 2.
and then we have to draw the graph of the given curve and the tangent line.
Explanation:
(a) we know the derivative of any curve represents the slope of the tangent line to the curve,
Therefore, firstly we will find the derivative
\(\begin{gathered} y=x^3-4x^2+2x-1 \\ \frac{dy}{dx}=3x^2-8x+2 \\ at\text{ x =a= 2} \\ \frac{dy}{dx}=3(2)^2-8(2)+2=12-16+2=-2 \\ \end{gathered}\)Therefore, slope of the tangent line is m = -2.
Now, the equation of the tangent line to the given curve is
\(y=f^{\prime}(a)(x-a)+f(a)\)Now we have,
\(\begin{gathered} f(a-2)=(2)^3-4(2)^2+2(2)-1=8-16+4-1=-5 \\ and\text{ f'\lparen a\rparen=-2} \end{gathered}\)Therefore, the equation of tangent line is
y = -2(x-2) + (-5)
y = -2x+ 4 -5
y = -2x-1
(b) Now we will draw the graph of the given curve and tangent line to the given curve as follows
The graph of the curve is represented by blue colour and the graph of the tangent line is represented by green colour.

A space shuttle 275 miles above the earth is orbiting the earth once every 4 hours. How far does the shuttle travel in 1 hour? (Assume the radius of the earth is 4,000 miles.) Answer exactly or round to the nearest mile
Answers
The space shuttle travels about 6713 miles per hour. Rounded to the nearest mile, this is approximately 6713 miles per hour.
What is a radius ?
In mathematics, the radius is a term used to describe the distance from the center of a circle or a sphere to any point on its surface. It is denoted by the letter "r".
The orbit of the space shuttle is circular, so the distance it travels in one orbit is equal to the circumference of the circle with a radius of 275 + 4000 = 4275 miles (275 miles above the Earth's 4000 mile radius).
The circumference of a circle is given by the formula C = 2πr, where r is the radius of the circle and π is the mathematical constant pi (approximately 3.14). Therefore, the distance traveled by the shuttle in one orbit is:
C = 2π(4275) ≈ 26851 miles
Since the shuttle orbits once every 4 hours, its average speed is:
distance/time = 26851/4 ≈ 6713 miles per hour
Therefore, the space shuttle travels about 6713 miles per hour. Rounded to the nearest mile, this is approximately 6713 miles per hour.
To learn more about Radius from given link.
https://brainly.com/question/13449316
#SPJ1
Kent is 12 4/5 years old. Lane is 1 1/6
Years Older than kent and jane
is 1 1/3 year older than lane
How old is jane?
Answers
Answer:
\(Jane = 15\frac{3}{10}\)
Step-by-step explanation:
Given
\(Kent = 12\frac{4}{5}\)
\(Lane = 1\frac{1}{6} + Kent\)
\(Jane = 1\frac{1}{3} + Lane\)
Required
Determine Jane's age
Substitute \(Kent = 12\frac{4}{5}\) in \(Lane = 1\frac{1}{6} + Kent\)
\(Lane = 1\frac{1}{6} + 12\frac{4}{5}\)
\(Lane = \frac{7}{6} + \frac{64}{5}\)
Take LCM
\(Lane = \frac{45+384}{30}\)
\(Lane = \frac{419}{30}\)
Substitute \(Lane = \frac{419}{30}\) in \(Jane = 1\frac{1}{3} + Lane\)
\(Jane = 1\frac{1}{3} + \frac{419}{30}\)
\(Jane = \frac{4}{3} + \frac{419}{30}\)
Take LCM
\(Jane = \frac{40+419}{30}\)
\(Jane = \frac{459}{30}\)
\(Jane = 15\frac{3}{10}\)
Solve the equation.
y + 3 = y +9
O y = 1
O y=3
O y = 6
O.y = 9
Answers
2y = 6
y = 3
Answer: y = 3
A running club has three types of
members: adults, juniors and children.
The ratio of juniors to children is 3 : 5.
The ratio of children to adults is 3 : 1.
What is the ratio of juniors to adults in its
simplest form?
Answers
We can conclude that the ratio of juniors to adults is 9:5 respectively.
What are ratios?An ordered pair of numbers a and b, represented as a / b, is a ratio if b is not equal to 0.
A proportion is an equation that sets two ratios at the same value.
For instance, you may express the ratio as 1: 3 (there are 3 girls for every boy) if there is only 1 boy.
There are 1 in 4 boys and 3 in 4 girls.
So, we know that:
Juniors to children = 3:5
Children to adults = 3:1
Now, calculate the ratio of Junoirs to adults as follows:
J:C = 3:5
C:A = 3:1
Then,
J:C:A
3:5:5
3:3:1
Add, and we get:
9:15:5
The ratio of juniors to adults is 9:5.
Therefore, we can conclude that the ratio of juniors to adults is 9:5 respectively.
Know more about ratios here:
https://brainly.com/question/12024093
#SPJ1
plz answer this question without links and files :)
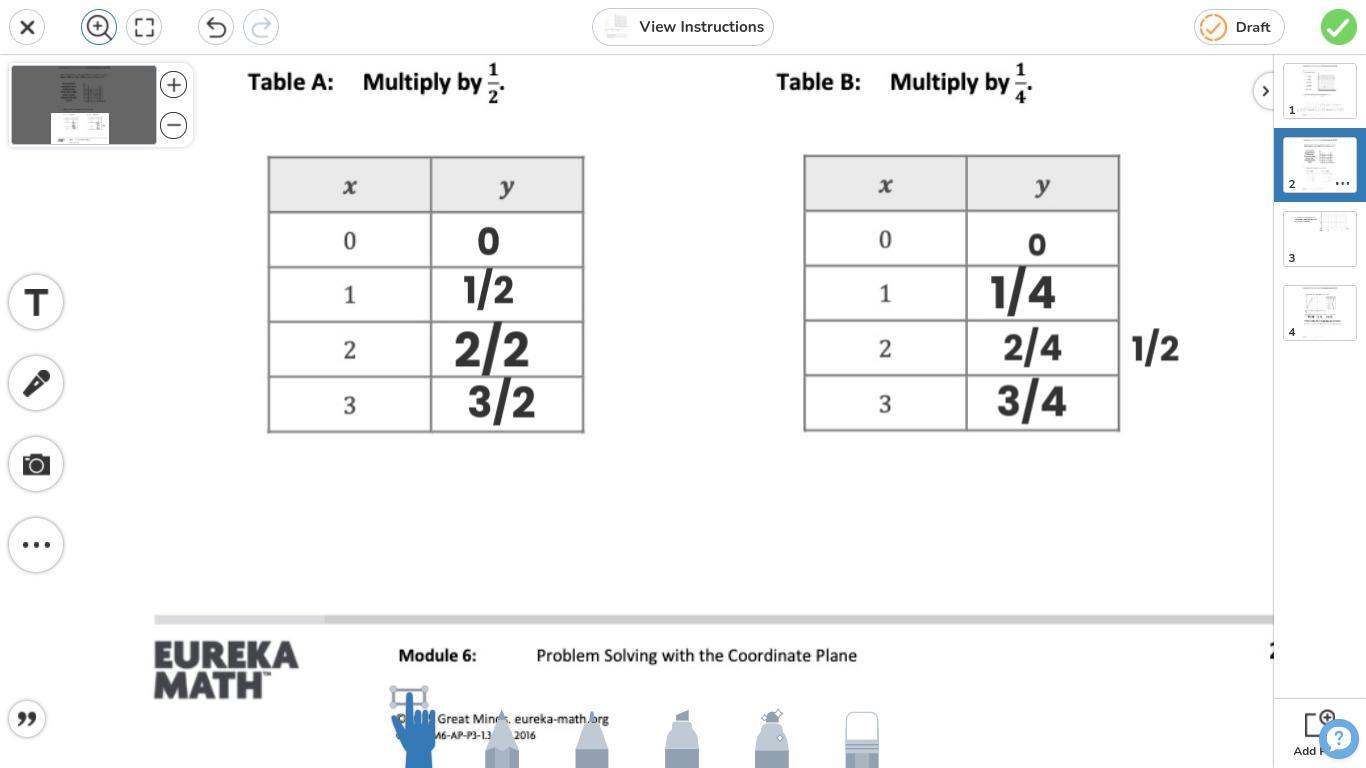
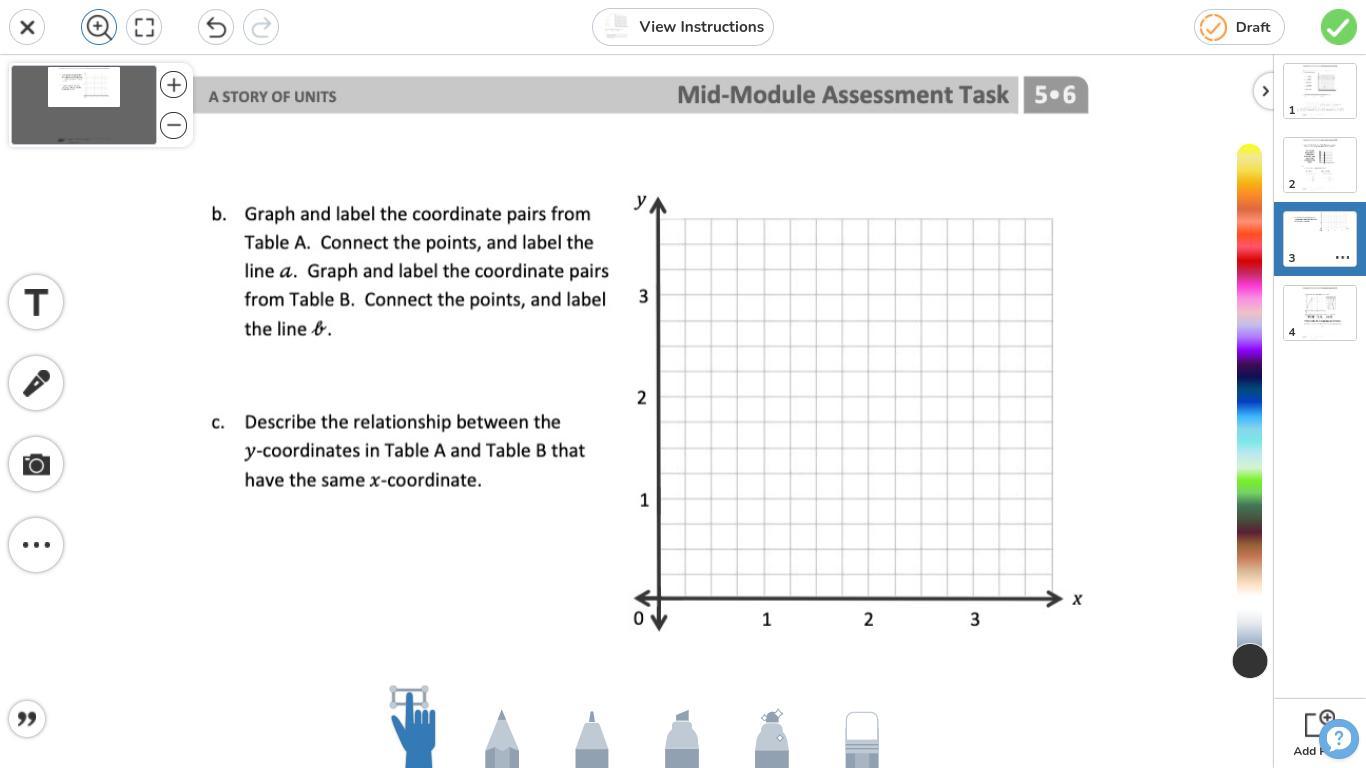
Answers
Answer:
The relationship between the y coordinates in table a and b is that they are parallel to each other on the graph.
Step-by-step explanation:
I have no idea what they are asking for I'm sorry
Please help!!!!!!!!!!

Answers
Answer: angle 1 = 51, angle 2 = 18, angle 3 = 123, angle 4 = 39
Step-by-step explanation:
72+57=129 180-129= 51 degrees for 1
90-72= 18 degrees for 2
180-57= 123 degrees for 3
123+18=141 180-141= 39 degrees for angle 4
Which scenario could be represented by this graph?
O A Mark leaves home and walks to a friend's house. He picks up his
friend and they return to Mark's house, where they stay for the
evening. The x-axis represents time; the yaxis represents the
distance from Mark's house
O B. Mark leaves home and starts walking to a friend's house, but he
has to return home when he realizes he has forgotten something
After returning home, he heads back out to his friend's house. The
x-axis represents time; the y-axis represents the distance from
Mark's house
OC. Mark leaves home and walks to a friend's house. They stay there
for an hour before returning to Mark's house. The x-axis represents
time; the y-axis represents the distance from Mark's house,
OD Mark leaves home and walks to a friend's house, but he gets lost
and goes too far. He then retraces his steps and arrives at his
friend's house, where he stays for the evening. The axis
represents time the y-axis represents the distance from Mark's
house

Answers
Answer:
the answer is d or b need help
Answer:D
Step-by-step explanation:
AP3X
Raghu purchased 234
pounds of rice. Belle purchased 54
as much as Raghu.
Complete the statement below to estimate how many pounds of rice Belle purchased.
CLEAR CHECK
Belle purchased about
pounds of rice.
I know this because
is
1
.
Answers
By fraction method, 55/16 pounds of rice Belle purchased.
In math, what is a fraction?
Part of a whole is a fraction. In mathematics, the number is represented as a quotient, where the numerator and denominator are divided. Both are integers in a simple fraction.
Whether it is in the numerator or denominator, a complex fraction contains a fraction. The numerator and denominator of a correct fraction are opposite each other.
= 2 3/4 * 5/4
= 5/4 * 2 + 5/4 * 3/4
= 5/2 + 5/4 * 3/4
= 5/2 + 15/ 4 * 4
= 5/2 + 15/16
common denominator and write the numerators above common denominator = 5 *8/16 + 15/16
= 40/16 + 15/16
= 40 + 15/16
= 55/16
Learn more about fraction
brainly.com/question/1301963
#SPJ1
What is the quotient of 3/4 divided by 5/4
Answers
Real-life Problems Question 10

Answers
Answer :
a) It is given that
Everyday a machine makes 500000 staples and puts them into the boxes.
The machine need 170 staples to fill a box
One box contans = 170 staples.
Total number of staples = 500000
Number of box required to fill 500000 staples = Total number of staples/No. of staples 1 box contains.
\( \: :\implies \) 500000 /170
\( :\implies \: \) 2941 (approx)
Therefore, 2941 boxes are required to fill with 500000 staples.
b) It is given that,
Each staple is made of 0.21 g of metal .
Total weight of metal = 1 kg = 1000 g
1 staple = 0.21 g
Number of staples = weight of metal/ Weight of 1 staple.
\( \: :\implies \) 1000/0.21
\( \: :\implies \) 4761 (approximately)
Therefore, 4761 staples can be made from 1 kg of the metal.
(-2,8) and (7, -8) find the distance between each pair of points
Answers
Answer:
√337 or about 18.36
Step-by-step explanation:
distance formula √((y2-y1)^2+(x2-x1)^2)
√(((8-(-8))^2+(-2-7)^2)
√(16^2+9^2)
√(256+81)
√337
What’s the answer to this

Answers
6. A bag contains an assortment of marbles. 3 marbles are swirled • 8 marbles are striped • 2 marbles are spotted A marble will be randomly selected from the bag. What is the probability that the marble selected will NOT be a striped marble? 5 F G 8 H
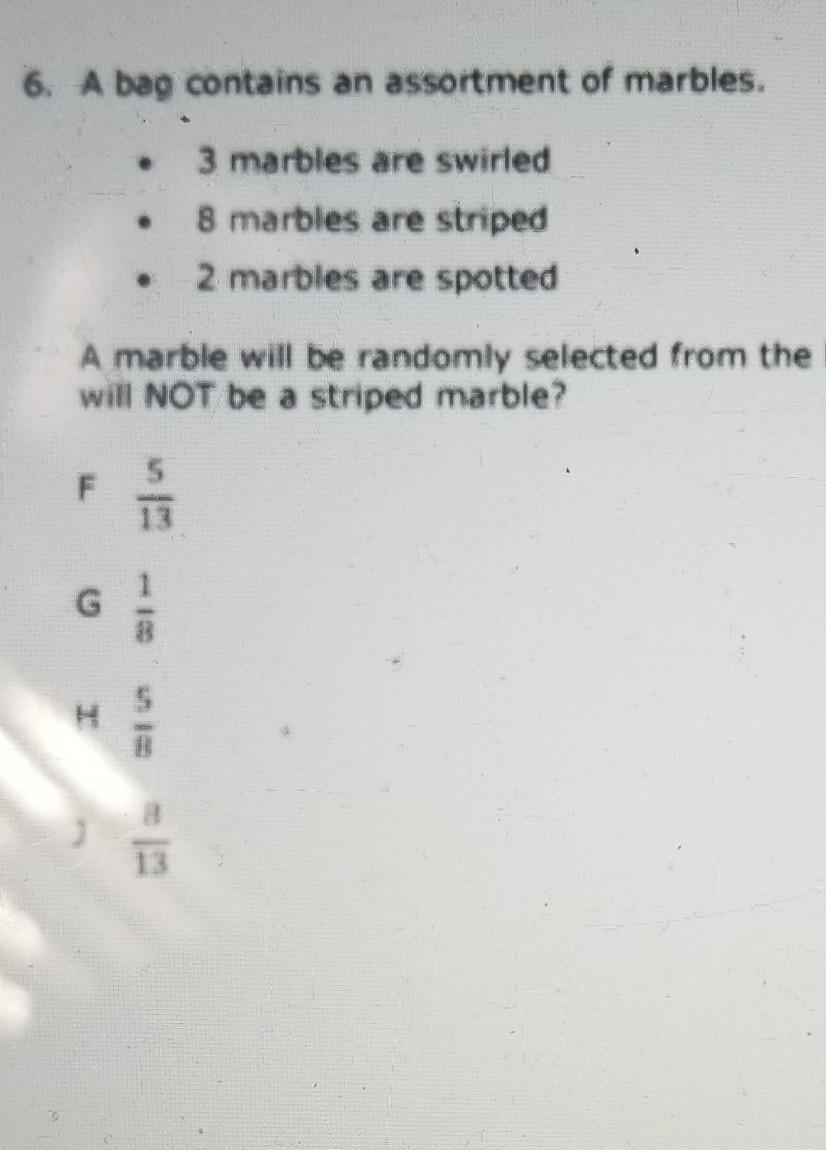
Answers
The probability that the marble selected will not be a striped marble is 5/13.
We have a bag. The bag contains an assortment of three types of marbles. There are three swirled marbles. The number of striped marbles is eight. The number of spotted marbles is two. A marble will be randomly selected from the bag. We need to find the probability that the marble selected will not be a striped marble. Let the probability of a striped marble be represented by P.
P = 8/(3 + 8 + 2) = 8/13
The probability that the marble selected will not be a striped marble is 1 - P = 1 - (8/13) = 5/13.
To learn more about probability, visit :
https://brainly.com/question/11234923
#SPJ9
one half cubed − 6 ÷ square root of 64
negative five eighths
negative 47 over 64
five eighths
47 over 64
Answers
Answer:
answer: negative five eighths
The solution to the expression one half cubed − 6 ÷ square root of 64 is A. negative five-eighths.
Given a fractional expression:
One half cubed − 6 ÷ square root of 64
It is required to find the value of the expression.
This can be numerically written as:
\((\frac{1}{2} )^3-6\div\sqrt{64}\)
It is known that:
\(\sqrt{64}=8\)
So, the expression can be written as:
\((\frac{1}{2} )^3-6\div8\)
Now, \((\frac{1}{2} )^3=\frac{1}{2^3}\)
\(=\frac{1}{8}\)
So, the expression becomes:
\((\frac{1}{8} )-6\div8\)
Using the BODMAS rule, division has to be done first before subtraction.
So, the expression becomes:
\((\frac{1}{8} )-\frac{6}{8}=-\frac{5}{8}\)
Hence, the correct option is A. negative five-eighths.
Learn more about BODMAS rule here :
https://brainly.com/question/29795897
#SPJ3
permieter of 2 rectangles is 54 cm.
work out the area of a square
Answers
The Area of Square is 81 cm².
let the side of the square which is length for both rectangles be a.
let the width of rectangle be x and y.
So, x+ y= a
sum of perimeters= 54
2 (a +x ) + 2 (a+ y) = 54
2a+ 2x + 2a+ 2y = 54
2a + 2a + 2(x+ y) = 54
4a + 2 (a) = 54
4a + 2a = 54
6a = 54
a= 54/6
a= 9
So, area of square
= 9 x 9
= 81 cm²
Learn more about Area here:
https://brainly.com/question/1631786
#SPJ1
what is six hundred eighty and fourteen thousandths written in standard form?
Answers
Answer:618.014
Step-by-step explanation: It may look like hundredths which is where must people mess up but it is instead thousandths.
Assume that SAT scores are normally distributed with mean mu equals 1518 and standard deviation sigma equals 325. If 1 SAT score is randomly selected, find the probability that it is greater than 1600. If 81 SAT scores are randomly selected, find the probability that they have a mean greater than 1600.
Answers
Answer:
\(P(X>1600)=P(\frac{X-\mu}{\sigma}>\frac{1600-\mu}{\sigma})=P(Z>\frac{1600-1518}{325})=P(z>0.252)\)
And we can find this probability using the z score formula and the complement rule and we got:
\(P(z>0.252)=1-P(z<0.252) =1-0.599= 0.401 \)
\( z =\frac{1600-1518}{\frac{325}{\sqrt{81}}}= 2.27\)
And we can find this probability using the z score formula and the complement rule and we got:
\(P(z>2.27)=1-P(z<2.27) =1-0.988=0.012\)
Step-by-step explanation:
Let X the random variable that represent the SAT scores of a population, and for this case we know the distribution for X is given by:
\(X \sim N(1518,325)\)
Where \(\mu=1518\) and \(\sigma=325\)
We want to find this probability:
\(P(X>1600)\)
And we can use the z score formula given by:
\(z=\frac{x-\mu}{\sigma}\)
Using this formula we got:
\(P(X>1600)=P(\frac{X-\mu}{\sigma}>\frac{1600-\mu}{\sigma})=P(Z>\frac{1600-1518}{325})=P(z>0.252)\)
And we can find this probability using the z score formula and the complement rule and we got:
\(P(z>0.252)=1-P(z<0.252) =1-0.599= 0.401 \)
For the other part we need to take in count that the distribution for the sampel mean if the sample size is large (n>30) is given by:
\(\bar X \sim N(\mu, \frac{\sigma}{\sqrt{n}})\)
And we can use the z score formula given by:
\(z=\frac{x-\mu}{\frac{sigma}{\sqrt{n}}}\)
And replacing we got:
\( z =\frac{1600-1518}{\frac{325}{\sqrt{81}}}= 2.27\)
And we can find this probability using the z score formula and the complement rule and we got:
\(P(z>2.27)=1-P(z<2.27) =1-0.988=0.012\)
a. How much warmer is 82 than 40?
b. How much warmer is 82 than -40?
a. What is the difference in height between 30 m up a cliff and 87 m up a cliff? What is the distance between these positions?
b. What is the difference in height between an albatross flying at 100 m above the surface of the ocean and a shark swimming 30 m below the surface? What is the distance between them if the shark is right below the albatross?
Answers
Answer:
a. 42
b. 122
a. 57
b. 130
Step-by-step explanation:
For problem A:
because both of these values have positive numbers, just use normal subtraction
82 - 40 = 42 degrees warmer
For problem B:
because we are subtracting a negative number from a positive number, we add both of these numbers because 82 - -40 can also be equal to 82 + 40
82 - -40 = 122
For problem A:
the sentences 30m up a cliff and 87m up a cliff are describing positive values.
87 - 30 = 57
For problem B:
Now in this problem, the sentence 100m above the surface is describing a positive value, but the sentence 30m below the surface describes a negative value
how do I know this?
if the sentences above the surface and below the surface are describing positive and negative values, then there has to be a neutral value ( which is 0)
0 meters = the surface, because they are using both positive and negative values, meaning that the surface is the neutral value
by using a number line, you can draw it out like this
below the surface-------------------------the surface----------------------------above the surface
-30--------------------------------------------0--------------------------------------------100
therefore, 100 - - 30 = 100 + 30 = 130
Please help me with this proof.

Answers
Answer:
See below
Step-by-step explanation:
For the second step, \(\angle T\cong\angle R\) by Alternate Interior Angles. The rest of the steps appear to be correct.
Mrs. Chu's famous peanut butter cookies call for 1 cup of peanut butter for every 1/2 of a cup of oil. Today, she wants to make a huge batch with 1 cup of oil. How much peanut butter should she use?
Answers
Answer:
she should use 2 cups of peanut butter
Step-by-step explanation:
to know the answer to that
use this equation (pb is peanut butter &o is oil)
1cup of pb=1/2 cup of o
?=1 cup of o
1×1÷1/2= 1×1×2/1=2co cups of pb
Find the angle on the unit circle

Answers
The angle on the unit circle is solved to be
56.01 degrees (to the nearest tenth)
How to find the angleTo find the angle of the terminal side through the given point on the unit circle, we can use the inverse trigonometric functions.
given that P = ((√5)/4, (√11)/4)
θ = arctan ((√11)/4 / (√5)/4)
θ = arctan((√11)/(√5))
θ ≈ 56.01 degrees
hence to the nearest tenth of a degree, the angle of the terminal side through the point P = ((√5)/4, (√11)/4) on the unit circle is approximately 56.01 degrees.
Learn more about unit circle at
https://brainly.com/question/30403151
#SPJ1
10x-5 9x+2 is my equation and I don’t know how to solve it I really need help,someone please help me solve it.
Answers
9514 1404 393
Answer:
x = 7
Step-by-step explanation:
You solve a linear equation by putting the variable on one side of the equal sign and a constant on the other side. Here, variables and constants are on both sides of the equal sign, so you need to separate them.
The basic idea is that you add the opposite of any term you don't want. Whenever you perform any operation (like "add"), you must do it to both sides of the equation.
We observe that x-terms have coefficients of 10 and 9. We choose to add the opposite of 9x to both sides:
10 -9x -5 = 9x -9x +2
x -5 = 2 . . . . simplify
Now, we still have -5 on the left, where we don't want it. So, we add its opposite (+5) to both sides:
x -5 +5 = 2 +5
x = 7 . . . . simplify
The solution is x = 7.
_____
Additional comment
If we were to end up with an x-coefficient other than 1, we would divide both sides of the equation by that coefficient. This will leave the x-term with a coefficient of 1.
A polyhedron with two parallel congruent faces called bases connected by parallelogram faces is called a...
Answers
Answer:
right prism
Step-by-step explanation:
If the faces are rectangles, then this prism is called a "right prism"