Answers
One way is to solve for the inverse of the first function
remember, to solve, replace f(x) or g(x) with y, switch x and y, solve for y and replace it with \(f^{-1} (x)\)
A.
\(f(x)=x/2+8\\y=x/2+8\\x=y/2+8\\x-8=y/2\)
\(2x-16=y\)
\(f^{-1}=2x-16\)
nope, not A
What is the inverse function?The inverse function of a function f is a function that undoes the operation of f. The inverse of f exists if and only if f is bijective, and if it exists, is denoted by \({\displaystyle f^{-1}.}\)
B.
\(f(x)=3x^3+16\\y=3x^3+16x=3y^3+16\\x-16=3y^3\\(x-16)/3=y^3\)
\(f^{-1}(x)=\sqrt[3]{((x-16)/3)}\)
nope, not the same
not B
C.
\(f(x)=18/x-9\\y=18/x-9\\x=18/y-9\\x+9=18/y\\y(x+9)=18\\y=18/(x+9)\\f^{-1}(x)=18/(x+9)\)
The correct, answer is C.
To learn more about the inverse function visit:
https://brainly.com/question/2972832
#SPJ1
Related Questions
in k-means clustering, suppose the number of clusters is equal to the number of data points (observations). then what will be the sum of squared errors within each group (or cluster)?
Answers
If the number of clusters in k-means clustering is equal to the number of data points, then each data point will form its own cluster. In this case, the sum of squared errors within each group will be zero, as there will be no other data points in the same cluster to calculate an error with.
The sum of squared errors within a cluster is a measure of how spread out the data points in that cluster are from the centroid (or center) of the cluster. When there is only one data point in a cluster, there is no deviation from the centroid, and therefore no error.
However, this scenario of having as many clusters as data points is not ideal for clustering analysis. The purpose of clustering is to group similar data points together based on their attributes, so having each data point in its own cluster defeats this purpose. In such a scenario, there is no useful information gained from the clustering analysis.
In practice, the number of clusters in k-means clustering is typically chosen based on other criteria, such as the elbow method or silhouette coefficient, to ensure that the resulting clusters are meaningful and informative.
learn more about k-means clustering here: brainly.com/question/30242059
#SPJ11
William earned $3,200 per month as a teacher for the ten months from September to June. Then he took a job as a barista at a local café, where he earned $2,000 per month during July and August. What was his average monthly pay for the 12 months?
Answers
Answer:
$3,000
Step-by-step explanation:
To find his average monthly pay, you have to find the total amount that Willian received in a year by multiplying his monthly salary as a teacher for 10 months and his salary as a barista for 2 months and adding up these numbers. Then, you have to divide the total amount he earned by 12 that is the number of months in a year:
($3,200*10)+($2,000*2)= $32,000+4,000=36,000
$36,000/12=$3,000
According to this, his average monthly pay for the 12 months was $3,000.
help fast plss!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
Answer:
d
Step-by-step explanation:
find the gradient that is perpendicular to a line with gradient minus 3
Answers
Answer:
perpendicular gradient = \(\frac{1}{3}\)
Explanation:
In parallel, the gradient is same. m1 = m2
using formula: m1 * m2 = -1
solve:
-3 * m2 = -1m2 = \(\frac{-1}{-3}\)m2 = \(\frac{1}{3}\)The percent of fat calories that a person consumes each day is normally distributed with a mean of about 33 and a standard deviation of about ten. Suppose that 9 individuals are randomly chosen. Let X = average percent of fat calories.(a) Give the distribution of X. (Round your standard deviation to two decimal places.) - ? (b) For the group of 9, find the probability that the average percent of fat calories consumed is more than six. (Round your answer to four decimal places.)
Answers
(a) The distribution of x is x ~ N\((33, 10^2)\)
(b) The probability that the percent of fat calories a person consumes is more than 6 is P(z > - 2.7)
Lower and Upper Quartiles:The lower quartile is the point that separates the lower 25% of the data from the rest. While the upper quartile separates the lower 75% (or upper 25%) from the rest of the data. The lower and upper quartiles are respectively known as the first and third quartiles.
Calories that a person each day is normally distributed.
Population mean, μ = 33
Population standard deviation, σ = 10
If "x" represent the percent of fat calories then the z - scores for "x" can be given as:
z = x - μ / σ
(a) The distribution of "x" will be normal with the mean equal to 33 and standard deviation equal to 10. It can be written as x ~ N\((33, 10^2)\)
(b) The probability that the percent of fat calories a person consumes is more than 6:
P(x > 6) = P \((z > \frac{6 - 33}{10} )\\\)
= P(z > - 2.7)
Learn more about Standard deviation at:
https://brainly.com/question/23907081
#SPJ4
Angles 1 and 2 are supplementary
Angle 1 = 30°
Answers
Answer:
Angle 2 = 150°
Step-by-step explanation:
▪︎ Measures of supplementary angles add up to 180°.
Therefore,
Angle 1 + Angle 2 = 180°
Angle 1 = 30°
30° + Angle 2 = 180°
Angle 2 = 180° - 30° = 150°
Simplify 6(3a - 8b + 2)
9a - 8b + 2
18a - 48b + 12
9a - 14b + 12
18a - 8b + 2
Answers
\( \sf = 6(3a - 8b + 2)\)
\( \sf = 18a - 48b + 12\)
Opsi : B
Answer:
Step-by-step explanation:
Distribute 6 to all terms in (3a - 8b + 2 )
6(3a - 8b + 2) = 6*3a - 6*8b + 6*2
= 18a - 48b + 12
Assume A is an n × n matrix. Answer "True" if the statement is always true, and "False" otherwise. a. If A is a stochastic matrix, then its 1-eigenspace must be a line. Choose ▼ b. If A is a stochastic matrix, then 1 must be an eigenvalue of A. Choose c. If A is a positive stochastic matrix, then repeated multiplication by A pushes each vector toward the 1-eigenspace. Choose d. If A is a square matrix, then A and A" must have the same eigenvalues. Choose ▼
Answers
The statements that is always true or false given that A is an n × n matrix are; A. True. B. True C. True, D. True
What should you know about n × n matrix?A. A stochastic matrix always has 1 as an eigenvalue, and the corresponding eigenvector forms a line, the 1-eigenspace. in other words, A stochastic matrix is a matrix whose rows sum to 1. This means that the sum of the elements in each row of A is equal to 1.
B. a stochastic matrix always has 1 as an eigenvalue. The eigenvalues of a matrix are the roots of its characteristic polynomial.
C. A positive stochastic matrix is a stochastic matrix whose entries are all non-negative. If A is a positive stochastic matrix, then repeated multiplication by A pushes each vector toward the 1-eigenspace.
D. For a square matrix, the eigenvalues of a matrix and its transpose are the same.
The above answer for D is based on the assumption that question D is
d. If A is a square matrix, then A and A^T must have the same eigenvalues.
Find more exercises on matrix;
https://brainly.com/question/11348342
#SPJ1
If the height of a cylinder is halved, its volume becomes how many times?
Answers
Answer:
\(volume \: of \: cylinder = \pi {r}^{2} h \\ if \ \: \: h \: \: is \: halved \: then \\ volume = \frac{\pi {r}^{2} h}{2} \)
hope my answer is correct
At 2:45 in the afternoon, the tree cast a 9-foot shadow. Just after sunrise, the shadow had been 24 feet. What was the % change in the shadow’s length?
Answers
1/4 > 1. Order the following rational numbers from greatest to least: 25% - 0.17 3 5 1.2 - 12 First convert these numbers to decimal form. Show your work below. You can write on the screen! Next, grab the numbers in the list and place them in order from GREATEST to LEAST!
Answers
Answer:
1.2, 3/5, 25%, 0.17, -12
Step-by-step explanation:
In order to put these from greatest to least, you must put these in like terms.
Since there are more decimals that other terms, we're going to convert them all to decimals.
25%= 0.25
0.17= 0.17
3/5= 0.60
1.2= 1.20
-12= -12.00
Now that we see which numbers are greater, we convert them back to their original terms and place them in order from greatest to least.
1.2, 3/5, 25%, 0.17, -12
Pleaseee help max points is the reward I really need help with this question and it says find leg 1 leg 2 and the distance please help

Answers
answer done last mai btaa dena correct hai
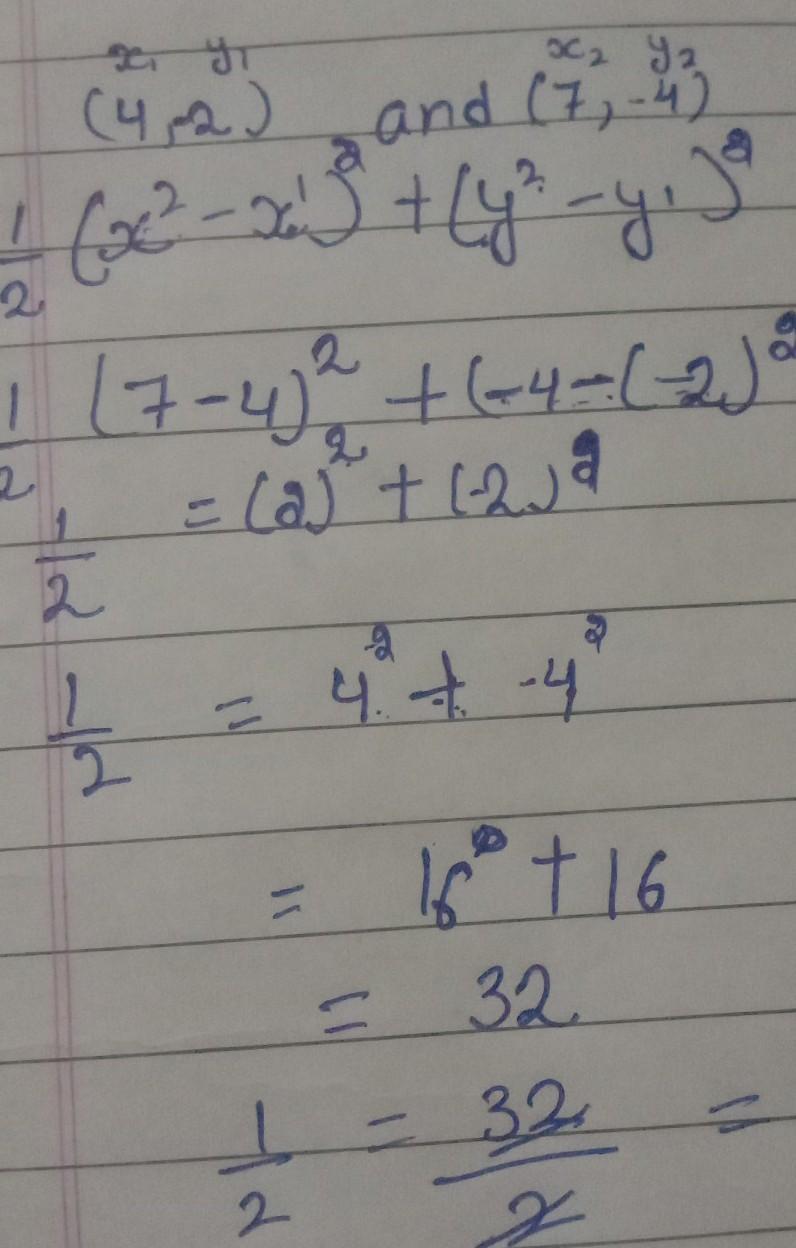
1/2 divided 2 equals= _____
Answers
Answer:
1/4
Step-by-step explanation:
half of a half is a fourth.
Answer:
1/4
Step-by-step explanation:
1/4 is half of 1/2
1/2 divided by 2/1
keep change flip
1/2 x 1/2 = (1x1=1, 2x2=4) 1/4
I Need Help With This Question

Answers
Answer:
Step-by-step explanation:
Dont do it. Just take the detention
2. You were 22 inches tall at birth, and 48 inches tall on your 8th birthday.
2a) On average, how many inches did you grow per year? (Hint: in 8 years 2 points
you grow a total of 26 inches) include units!!
Answers
Answer:
3.25
Step-by-step explanation:because you have to divide the years with the inches so in each year i would grow about 3.25 inches
Describe the process of measuring using a 25 mL graduated cylinder. To what decimal place must you estimate using the 25 mL graduated cylinder?
Answers
The process of measuring using a 25 mL graduated cylinder involves pouring the liquid into the cylinder and reading the volume at the meniscus. When using a 25 mL graduated cylinder, you must estimate to the nearest tenth of a milliliter (0.1 mL).
When measuring using a 25 mL graduated cylinder, the following process is typically followed:
Prepare the graduated cylinder: Ensure that the graduated cylinder is clean and dry before use. Check for any cracks or chips that could affect the accuracy of the measurement.
Read the initial volume: Hold the graduated cylinder at eye level and carefully pour the liquid into it until the desired volume is reached. Align the bottom of the meniscus (the curved surface of the liquid) with the closest graduation line.
Estimate the additional volume: If more liquid is needed, pour it slowly into the graduated cylinder while keeping it at eye level. As the liquid level rises, read the volume by aligning the bottom of the meniscus with the closest graduation line.
Take the final volume measurement: Once you have added the desired amount of liquid, read the final volume by aligning the bottom of the meniscus with the closest graduation line.
To estimate using the 25 mL graduated cylinder, you must estimate to the nearest tenth of a milliliter (0.1 mL) or the first decimal place.
This means that if the liquid level falls between two graduation lines, you estimate the value based on the markings on the cylinder.
For example, if the liquid level is slightly above the 5 mL line but not quite at the 6 mL line, you would estimate the volume as 5.2 mL or 5.3 mL, depending on the level of precision required.
Learn more about meniscus from the given link
https://brainly.com/question/10868896
#SPJ11
Evaluate. x =2 and y=-1
(3x)² (y) I need help pleaseeee

Answers
Answer:
- 36
Step-by-step explanation:
(3x)² (y) ← substitute x = 2, y = - 1 into the expression
= (3(2))² (- 1)
= (6)² × - 1
= 36 × - 1
= - 36
Jerome photographed an aquarium that measured 12 inches by 18 inches by 24 inches. Lim photographed an aquarium that was 12 inches by 30 inches by 12 inches. Both aquariums are rectangular prisms. How much more volume does Jerome’s aquarium have than Lim’s?
Answers
Answer:
the answer is 864 in3
Step-by-step explanation:
Jerome photographed an aquarium that measured 12 inches by 18 inches by 24 inches.
So V=LxWxH....
12 x 18 x 24= 5,184
Then...
Lim photographed an aquarium that was 12 inches by 30 inches by 12 inches.
So= V=LxWxH
12 x 30 x 12=4,320
And they need to see who has more so 5,184-4,320=864in3
I hope this helps also Into Math said it was correct :)
Which equation would be used to generate the data in the following table?

Answers
Answer:
D. y = 8x
Step-by-step explanation:
\(\mathrm{y(out put) = x(in put) \times 8}\)
We need to attach a support wire to Glendale's flagpole, which is 24 feet high. The
wire must make an angle of 50 degrees with the ground, How long must the wire
be? Round your answer to one decimal place.
Upload a Picture of your answer
Answers
Step-by-step explanation:
this creates a right-angled triangle.
the right angle (90°) being the angle between flag pole and ground.
the angle ground-wire is 50°.
because we know that the sum of all angles in a triangle is always 180°, we know then that the angle flagpole-wire is
180 - 90 - 50 = 40°
so, we have the situation to know 1 side and all angles.
to get the other sides we use best the law of sine :
a/sin(A) = b/sin(B) = c/sin(C)
where the sides and related angles are always opposite of each other.
in our case now we have
24/sin(50) = wire/sin(90) = wire/1 = wire = 31.32977494... ft
so, the rounded answer is that the wire must be
31.3 ft long
A line passes through the points (5,18 ) and(8,21) Write a linear function rule in terms of x and y for this line.
Answers
The equation of the line that passes through the points (5,18) and (8,21) is y = x + 13.
What is an equation of the line?An equation of the line is defined as a linear equation having a degree of one. The equation of the line contains two variables x and y. And the third parameter is the slope of the line which represents the elevation of the line.
The general form of the equation of the line:-
y = mx + c
m = slope
c = y-intercept
Slope = ( y₂ - y₁ ) / ( x₂ - x₁ )
Given points are (5,18 ) and (8,21). The equation of the line will be written as,
Slope = ( 21 - 18 ) / ( 8 - 5 )
Slope = 1
The y-intercept will be calculated as,
y = mx + c
18 = 5 + c
c = 13
The equation of the line is written as,
y = x + 13
To know more about an equation of the line follow
https://brainly.com/question/18831322
#SPJ1
Find the value of y, x, w, and z.

Answers
The angle measures are given as follows:
x = 49º.y = 49º.z = 98º.How to obtain the angle measures?For the measures of x and y, we have that they are congruent, as they are the base angles of an isosceles triangle with a top angle of 82º.
An isosceles triangle has two equal angle measures, and the sum of the measures of the internal angles of a triangle is of 180º, hence the value of x, and consequently the value of y, is obtained as follows:
x + y + 82 = 180
2x = 98
x = 49º.
For the value of z, we consider the ray at the center, formed by two pairs of vertical angles, hence:
2z + 2(82) = 360
z = (360 - 2 x 82)/2
z = 98º.
More can be learned about angle measures at https://brainly.com/question/30644403
#SPJ1
chegg if other factors are held constant, increasing the sample size for a chi-square test for independence will increase the likelihood of rejecting the null hypothesis.
Answers
Increasing the sample size for a chi-square test for independence, while holding other factors constant, increases the likelihood of rejecting the null hypothesis because as the sample size increases, the test becomes more sensitive to detecting small deviations from the expected frequencies.
In a chi-square test for independence, the null hypothesis assumes that there is no association between two categorical variables.
The test compares the observed frequencies in a contingency table to the expected frequencies under the assumption of independence. The chi-square test statistic measures the discrepancy between the observed and expected frequencies.
When the sample size is small, the test may not have enough power to detect a significant departure from the null hypothesis, even if such a departure exists in the population.
However, as the sample size increases, the test becomes more capable of detecting smaller deviations from independence, increasing the likelihood of rejecting the null hypothesis when there is a true association between the variables.
Therefore, increasing the sample size can improve the statistical power of the chi-square test and increase the likelihood of rejecting the null hypothesis, assuming other factors remain constant.
To know more about sample size refer here:
https://brainly.com/question/30100088#
#SPJ11
the scatterplot below shows the amount of time a trumpet player spends practicing a song, and the number of incorrect notes she plays while performing that song. Based on the graph, how many incorrect notes will she play if the practice time 7 1/2 hours
Answers
Answer:
10
Step-by-step explanation:
Please help me to solve this

Answers
Answer:
x = -5, 6
Step-by-step explanation:
\(x^{2} - x - 30 = 0\\(x-6)(x+5) = 0\\x = -5, 6\)
1 of 6
The following list shows how many brothers and sisters some students have:
2, 4, 3, 3, 4, 2, 4, 3, 3, 2, 3, 4
State the mode.
>
Answers
It's too short. Write at least 20 characters to explain it well.
Manny has car insurance and was in an accident with a bill totaling $11,500. The insurance company says he needs to pay the first $1000. What does the $1000 represent?.
Answers
Answer:
Deductible
Step-by-step explanation:
you pay the first $1,000 of covered services yourself
$1000 represents the deductible amount.
In the case of an accident, the policyholder must pay a deductible as the first amount; the insurance company will only cover any expenses (losses) incurred after the deductible has been paid by the policyholder.
The consumer can first set his deductible while purchasing insurance.
Smaller deductibles often result in higher rates, and larger deductibles frequently result in lower premium payments.
The insurance company has asked Manny to pay the first $1000 in an instance when he was involved in an accident and incurred charges totaling $11,500. The $1,000 deductible amount.
Hence, the answer is deductible amount.
Learn more about deductible amount here:
https://brainly.com/question/30098276
#SPJ6
6.2.21 if (x1, . . . , xn) is a sample from an n(μ, 1) distribution where μ>=0 is unknown, determine the MLE of μ.
Answers
Since μ≥0, if the calculated μ_MLE is negative, set the MLE to 0 as the final answer: μ_MLE = max(0, Σ(xi) / n).
Based on the given information, we have a sample (x1, ..., xn) from a normal distribution N(μ, 1) with an unknown mean μ≥0 and a known variance of 1. To determine the Maximum Likelihood Estimator (MLE) of μ, we follow these steps:
1. Write down the likelihood function, which is the product of the probability density functions (PDF) for the normal distribution: L(μ) = ∏[1/(√(2π)) * exp(-(xi - μ)² / 2)]
2. Take the natural logarithm of the likelihood function to get the log-likelihood function: log L(μ) = Σ[-(xi - μ)² / 2 - log(√(2π))]
3. Differentiate the log-likelihood function with respect to μ and set the result to zero to find the maximum: d(log L(μ))/dμ = Σ[2(xi - μ)] = 0
4. Solve for μ: μ_MLE = Σ(xi) / n
The MLE of μ is the sample mean, which is the sum of the xi values divided by the sample size n. However, since μ≥0, if the calculated μ_MLE is negative, set the MLE to 0 as the final answer: μ_MLE = max(0, Σ(xi) / n)
To determine the maximum likelihood estimator (MLE) of μ in this scenario, we need to first calculate the likelihood function. Since (x1, . . . , xn) is a sample from an n(μ, 1) distribution, the likelihood function can be expressed as:
L(μ|x1, . . . , xn) = (2π)^(-n/2) exp(-(1/2)Σ(xi - μ)^2)
To find the MLE of μ, we need to maximize this likelihood function with respect to μ. To do so, we take the derivative of the likelihood function with respect to μ and set it equal to zero:
d/dμ L(μ|x1, . . . , xn) = Σ(xi - μ) = 0
Solving for μ, we get:
μ = (1/n)Σxi
Therefore, the MLE of μ in this scenario is the sample mean, (1/n)Σxi. Note that since we do not know the true value of μ, we cannot substitute it into the likelihood function to obtain a numerical value for the maximum likelihood. Rather, we can only determine the MLE in terms of the sample and the distribution.
Learn more about function here: brainly.com/question/12431044
#SPJ11
Use the following information to answer the question that follows:
5 years ago Mayra began depositing money into a bank account every quarter that earns 6% compounded
quarterly. The account now has $6000 in it. How much did Mayra deposit into the account quarterly?
For the question above, what is the value of n?
A. n=52
B. n=1
C. n=NA
D. n=12
E. n=4

Answers
Answer:
E. n=4
Step-by-step explanation:
"compounded quarterly" meaning 4.
Option E is correct. The amount Mayra deposited into the account quarterly is $1,146.35 where the value of n is 4
In order to get the amount compounded quarterly, we will use the compounded interest formula as shown:
A = P(1+r/n)^nt where:
A is the amount after 5 years = $6000
r is the rate (in %) = 6% = 0.06
n is the compounding time = 1/4 (quarterly)
t is the time taken (in years) = 5 years
Required
Amount invested quarterly.
First, we need to get the amount initially invested
Substitute the given values into the formula;
6000 = P(1+0.06(4))^{5/4)}
6000 = P(1+0.24)^1.25
6000 = P (1.24)^1.25
6000 = 1.3085P
P = 6000/1.3085
P = $4,585.40
The amount initially deposited will be $4,585.40
The amount deposited quarterly = P/n where n = 4
Amount deposited quarterly = $4,585.40/4
Amount deposited quarterly = $1,146.35
Therefore the amount Mayra deposited into the account quarterly is $1,146.35 where the value of n is 4.
Learn more here: https://brainly.com/question/18456266
question is attached

Answers
Answer:
31
Step-by-step explanation:
The two angles are equal so
8x-1 = 5x+11
Subtract 5x from each side
8x-5x-1 = 5x-5x+11
3x -1 =11
Add 1 to each side
3x -1+1 = 11+1
3x = 12
Divide by 3
3x/3 = 12/3
x= 4
We want to find
WZY
WZY = 5x+11
= 5(4)+11
=20+11
=31
