Which sentence can represent the inequality 2.4 (6.2 minus x) greater-than negative 4.5?

Answer:

4

Step-by-step explanation:

its 4 duh

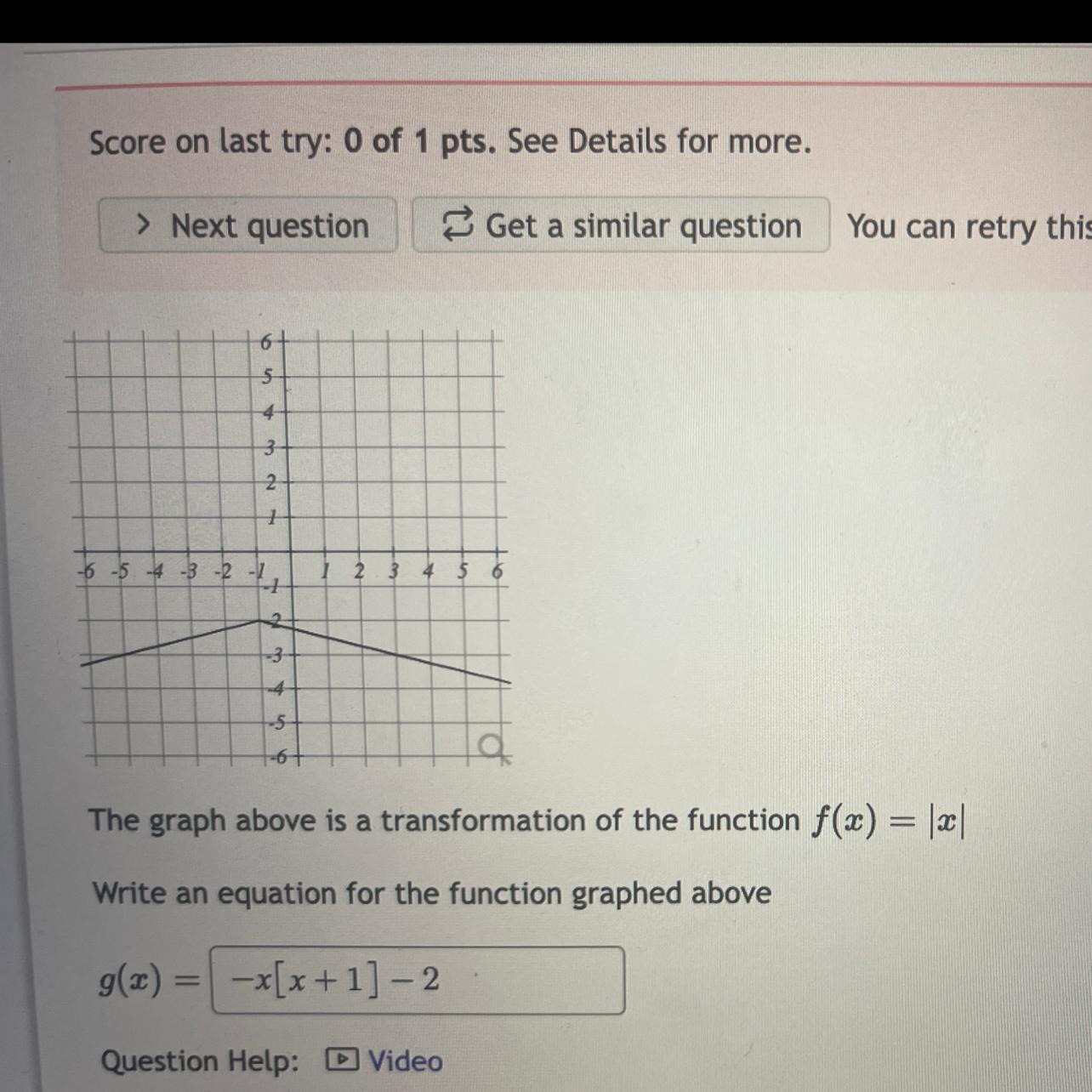
Answer:

Step-by-step explanation:

2 + 2 = 4

Answer:

108 inches²

Step-by-step explanation:

Rectangular prism = cuboid

To find how much paper is required to cover the box, we need to find the TSA of the cuboid.

TSA of cuboid = 2 [LB + LH + HB] = 2 [ (3×4) + (3×6) + (4×6) ] = 2 [ 12+18+24 ] = 2 × 54 = 108 inches²

Alexa and Raymond spent the same amount of money at the art store.

Alexa bought a paint brush for $8 and 4 jars of pant.

Raymond bought a paintbrush for $5 and 6 jars of paint

Let the cost of each jar of paint be x

For Alexa,

Since, she bought a paintbrush for $8 and 4 jars of paint

Total cost = y

Total cost = cost of paint brush + number of jars of paint x cost of each jar of paint

Since the cost of each jar of paint = x

total cost = 8 + 4 * x

y = 4x + 8----------- Alexa total cost equation

For Raymond,

He bought a paint brush for $5 and 6 jars of paint

Since, the cost of each jar of paint = x

Total cost = y

y = 6 * x + 5

y = 6x + 5 ---------- Raymond equation

The x - variable is the cost of each jar of paints

The true statement is (c) No; the slopes of segment EF and segment DF are not opposite reciprocals.

Right triangles have a pair of perpendicular lines

Coordinates

The coordinates are given as:

Start by calculating the slopes of lines DF and EF using:

\(m = \frac{y_2 -y_1}{x_2 -x_1}\)

So, we have:

\(m_{DF} = \frac{0 + 1}{0 +2}\)

\(m_{DF} = \frac{1}{2}\)

Also, we have:

\(m_{EF} = \frac{0 -2 }{0+2}\)

\(m_{EF} = \frac{-2 }{2}\)

\(m_{EF} = -1\)

For the triangle to be a right triangle, then the calculated slopes must be opposite reciprocals.

i.e.

\(m_1 = -\frac{1}{m_2}\)

By comparison, the slopes of both lines are not opposite reciprocals.

Hence, the true statement is (c)

Read more about right triangles at:

https://brainly.com/question/17972372

Answer:

c

Step-by-step explanation:

Answer:

5.4

Step-by-step explanation:

square of 29 = 5.385164807

5.385164807 estimated is 5.4

We are asked to decide on an inequality based on a graph.

The correct inequality among the listed ones is -6 < -4

and corresponds to the following graph:

If a polynomial function has integer coefficients, the every rational zero of the function has the form p/q, where p is a factor of the constant term and q is a factor of the leading coefficient.

The rational zero theorem says that if a polynomial has integer coefficients then any rational zeros must be of the form p/q where p is the factor of the constant term and q is the factor pf the leading coefficients.

The rational zero theorem is used to determine the rational roots of a polynomial function.

Rational Zero Theorem statement:-

The rational zero theorem states that each rational zero(s) of a polynomial wit integer coefficients

f(x) = anxⁿ + an-1xⁿ⁻¹ + ... + a₂x² + a₁x + a₀ is of the form p/q where,

p is a factor of the constant a₀,

q  is a factor of the leading coefficient an,

and p and q are relatively prime.

To know more about rational here

https://brainly.com/question/29155547

#SPJ4

Answer:

A rectangle of 10.6 x 11.4 dimensions.

Step-by-step explanation:

(5.3*2)*(5.7*2)=5.3*4*5.7=10.6x11.4.

Answer:

4/9 = 1/2 x

Step-by-step explanation:  2.84 sands

We can approach this problem by breaking down the two displacements of the ship into their respective x- and y-components and then adding them together to find the net displacement.

For the first displacement, the ship traveled 25° South of West for 250 miles. This can be broken down into an x-component and a y-component as follows:

x = 250 cos(25°) (to the west) y = -250 sin(25°) (to the south)

For the second displacement, the ship changed direction to 70° East of South and traveled 45 miles further. This can also be broken down into an x-component and a y-component:

x = 45 cos(70°) (to the east) y = -45 sin(70°) (to the south)

To find the net displacement, we can add the x-components and y-components separately:

total x = 250 cos(25°) + 45 cos(70°) total y = -250 sin(25°) - 45 sin(70°)

We can use these values to find the distance of the ship from its starting point by using the Pythagorean theorem:

distance = sqrt((total x)^2 + (total y)^2)

Substituting the values from above and evaluating:

distance = sqrt((250 cos(25°) + 45 cos(70°))^2 + (-250 sin(25°) - 45 sin(70°))^2)

distance ≈ 272.8 miles

To find the direction of the ship from its starting point, we can use the inverse tangent function to find the angle:

angle = atan(total y / total x)

Substituting the values from above and evaluating:

angle ≈ -65.1°

Since the angle is negative, we know that the direction is to the west of south. Therefore, the ship is approximately 272.8 miles away from its starting point in a direction that is 65.1° west of south.

Answer:

A. addition property of equality

Step-by-step explanation:

To make x stand alone, "5" was added to both sides of the equation. The property that is applied here is the addition property of equality.

Adding "5" to both sides of the equation makes the equation balanced.

The answer is: A. addition property of equality

An equation for the function graphed above include the following: g(x) = -1/4|x + 1| - 2.

By critically observing the graph of this absolute value function, we can reasonably infer and logically deduce that the parent absolute value function f(x) = |x| was vertically compressed by a factor of 1/4, reflected over the x-axis, followed by a vertical translation 2 units down, and then a horizontal translation to the left by 1 unit, in order to produce the transformed absolute value function as follows;

f(x) = |x|

y = A|x + B| + C

g(x) = -1/4|x + 1| - 2

In conclusion, the value of the variables A, B, and C are -1/4, 1, and 2 respectively.

Read more on absolute value function here: brainly.com/question/28308900

#SPJ1

Answer: -27

Step-by-step explanation: Use inductive reasoning to predict the most probable next number in the list.

3, 9, -3, 3, -9, -3, -15, -9, -21, ?

We can start by looking at the differences between consecutive terms in the list:

9 - 3 = 6 -3 - 9 = -12 3 - (-3) = 6 -9 - 3 = -12 -3 - (-9) = 6 -15 - (-3) = -12 -9 - (-15) = 6 -21 - (-9) = -12

Notice that the differences alternate between positive 6 and negative 12. This suggests that the pattern involves adding 6, then subtracting 12, and then adding 6 again. Applying this pattern to the last term in the list (-21), we get:

-21 + 6 = -15 -15 - 12 = -27 -27 + 6 = -21

Therefore, we predict that the most probable next number in the list is -27.

An equation of the line that goes through the point (-1, -3) and (3, 5) is y = 2x - 1.

An equation of the line in slope-intercept form that is perpendicular to the equation for obstacle 1 is y = -x/2 + 3.

In Mathematics, the point-slope form of a straight line can be calculated by using the following mathematical expression:

y - y₁ = m(x - x₁) or \(y - y_1 = \frac{(y_2- y_1)}{(x_2 - x_1)}(x - x_1)\)

Where:

At data point (-1, -3), a linear equation in slope-intercept form for this line can be calculated by using the point-slope form as follows:

\(y - y_1 = \frac{(y_2- y_1)}{(x_2 - x_1)}(x - x_1)\\\\y - (-3) = \frac{(5- (-3))}{(3-(-1))}(x -(-1))\\\\y +3 = \frac{(5+3)}{(3+1)}(x +1)\)

y + 3 = 2(x + 1)

y = 2x + 2 - 3

y = 2x - 1

In Mathematics, a condition that must be met for two lines to be perpendicular is given by:

m₁ × m₂ = -1

2 × m₂ = -1

m₂ = -1/2.

At point (-4, 5), an equation of the line can be calculated by using the point-slope form as follows:

y - y₁ = m(x - x₁)

y - 5 = -1/2(x + 4)

y = -x/2 - 2 + 5

y = -x/2 + 3

Read more on point-slope here: brainly.com/question/24907633

#SPJ1

Answer:

---------------------

Formula for area of a rectangle with dimensions l and w is:

Substitute 10 for l and 4 for w:

Answer:

3, 7

Step-by-step explanation:

"Zeros" means solutions to the equation f(x) = 0.  In other words, what are the values of  x  that make the function's value equal to zero?

This one can be solved by factoring.

\(x^2-10x+21=0\\(x-7)(x-3)=0\\x-7=0 \text{ or } x-3=0\\x=7 \text{ or } x=3\)

Answer: 0

Step-by-step explanation:

1/2(2x+5)=3/4(x+1)+5/2

distribute 1/2 to 2x and 5

distribute 3/4 to x and 1

1/4x+5/2=5/2

subtract 5/2 to 5/2

1/4=0

multiply 1/4 by the reciprocal

4/1*1/4=0*4/1

Answer= 0

Answer:

dA(s) = 22,917 cm²     maximum error

dA(s) /A(s) = 0,01389   or 1,38 %    relative error

Step-by-step explanation:

The Volume of a sphere is:

V(s) = 4/3)*π*r³       where  r is the  radius of circumference

If the length of circumference is 72 cm then

L (c) = 72   = 2*π*r

r  = 72/2*π

r = 72/ 6,28      ⇒  r = 11,46 cm

And

L(c)  = 2*π*r

Differentiation on both sides of the equation give:

dL (c) = 2*π*dr    

dr  =  dL(c) /2*π

dr = 0,5 / 6,28     ⇒  dr = 0,07961

The surface area Is:

A (s) = 4*π*r²

And the maximum or absolute error is

dA(s)  = 8*π*r*dr

dA(s) = 22,917 cm²

The relative error is   dA(s) /A(s)  

dA(s) /A(s) = 8*π*r*dr/ 4*π*r²

dA(s) /A(s) = 2*(0,07961)/ (11,46)

dA(s) /A(s) = 0,01389   or 1,38 %

\(\qquad \qquad \textit{inverse proportional variation} \\\\ \textit{\underline{y} varies inversely with \underline{x}} ~\hspace{6em} \stackrel{\textit{constant of variation}}{y=\cfrac{\stackrel{\downarrow }{k}}{x}~\hfill } \\\\ \textit{\underline{x} varies inversely with }\underline{z^5} ~\hspace{5.5em} \stackrel{\textit{constant of variation}}{x=\cfrac{\stackrel{\downarrow }{k}}{z^5}~\hfill } \\\\[-0.35em] ~\dotfill\)

\(\stackrel{\textit{"y" varies inversely with "x"}}{y = \cfrac{k}{x}}\hspace{5em}\textit{we also know that} \begin{cases} x=4\\ y=16 \end{cases} \\\\\\ 16=\cfrac{k}{4}\implies 64 = k\hspace{9em}\boxed{y=\cfrac{64}{x}} \\\\\\ \textit{when x = 32, what's "y"?}\qquad y=\cfrac{64}{32}\implies y=2\)

Answer:

Center ( -8, 1 )

Radius ( 13 )

Answer:

191cm^2

Step-by-step explanation:

Answer:

2

Step-by-step explanation:

they are x² and 3x

please mark as the Brainlist

Answer:

10(x + 30)

Step-by-step explanation:

10x + 300

Both terms have 10 in common, so you can factor out 10.

10x + 300 = 10(x + 30)

Answer: gurl you think i know

Step-by-step explanation:

Given data:

The given length of CW is CW=15 units.

The expression for the length of WX is,

Substitute 15 units for CW in the above expression.

Thus, the WX length is 5 units.

9514 1404 393

Answer:

  {1, 5, 7}

Step-by-step explanation:

For x=0, y = 2·0 +1 = 1

For x=2, y = 2·2 +1 = 5

For x=3, y = 2·3 +1 = 7

The range is the list of y-values, so is {1, 5, 7}.

Answer:

A'(-4,-3)

Step-by-step explanation:

use formula of reflection over y axis

(x,y)=(-x,y)

A(4,-3)=A'(-4,-3)

the answer is (-4,-3).

When using simulation models for random sampling, we can develop the margin of error by multiplying the critical value by the standard error.

This is a measure of the error that we get when we use a random sampling model.

It can be found by the formula:

= Critical value x Standard error

If using a z-test, the critical value would be z and the standard error would be (σ / √n). The margin or error would therefore be:

= z (σ / √n)

Find out more on margin of error at https://brainly.com/question/24289590.

#SPJ1

Answer:

Let's simplify step-by-step.

−19+4k−15k−k−9

=−19+4k+−15k+−k+−9

Combine Like Terms:

=−19+4k+−15k+−k+−9

=(4k+−15k+−k)+(−19+−9)

=−12k+−28

Answer:

=−12k−28

Step-by-step explanation:

Answer:

Step-by-step explanation:

i donot knpw