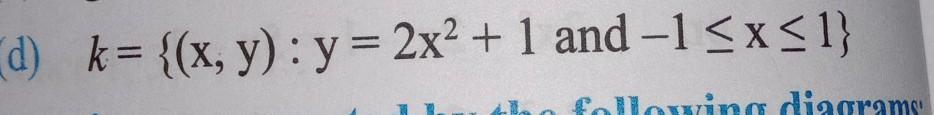WILL MARK BRAINLEST!!!
find the domain and range of following ​

Answer:

the asswer is 1 2 4

Step-by-step explanation:

1×20=30

2×10=20

4×5=2

The difference between the median math test score in the morning and the afternoon is 9.5

The median can simply be described as the middle number in a given set of data when the values are arranged in an order from least to the greatest values.

From the information given, we have that;

The math scores for the afternoon test were;

55, 70, 76, 85, 95

The math scores for the morning test were;

70, 80.5, 85.5, 90.5 and 95.5

Hence,

The median for the afternoon test = 76

The median for the morning test =85.5

The difference between the values would be = 85.5 - 76 = 9. 5

Read more about median at: https://brainly.com/question/26177250

#SPJ1

A²+B²= C²

31²+ 21²= z²

961+441 = z²

1402= z²

z= 37.443290454

Answer:

[2] It shows the commutative property over addition

[3] -5/6

[4] A. 6/7 and B. -101/213

[5]  Refer to picture below

[6] True, 1/2 *(-2/3*1/4) = (1/2*-2/3)*1/4.

Step-by-step explanation:

[3] 5/8 × 8/-6

Simplify

\(\frac{5}{8}\left(-\frac{4}{3}\right)\)

\(=-\frac{5}{6}\)

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

[4] -6/7

Opposite

6/7

x + ( - 6/7 ) = 0

⇒ x = 6/7

Hence additive inverse of - 6/7 is 6/7

101/213

Opposite

-101/213

x + (101/213)=0

⇒ x = -101/213

Hence additive inverse of 101/213 is -101/213

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

[6] Since x = 1/2 , y = -2/3 and z = 1/4

x * (y*z)=(x*y)*z

Substitute:

1/2 *(-2/3*1/4) = (1/2*-2/3)*1/4

-1/12 = - 1/12

TRUE

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

~Lenvy~

Answer:

3 2-pt shots, 4 3-pt shots

Step-by-step explanation:

2x + 3y = 18

x + y = 7, so x = 7 - y

Substitute in for x

2(7 - y) + 3y = 18

14 - 2y + 3y = 18

14 + y = 18

y = 4

Now put 4 in for y to solve for x

2x + 3(4) = 18

2x + 12 = 18

2x = 6

x = 3

Answer:

80/100 is 0.8

Step-by-step explanation:

sorry if I'm wrong

Answer:

C) 169 square units

Step-by-step explanation:

The formula for the area of a square is A = a² where a is one side of the square.

To find the length of one side of the square, use the distance formula for two points. I will use the points (-8, 3) and (4, 8).

d = √((x₂ - x₁)² + (y₂ - y₁)²)

d = √((4 - (-8)² + (8 - 3)²)

d = √((12)² + (5)²)

d = √(144 + 25)

d = √(169)

d = 13

Now since all of the sides of the square equal that value (13), plug it into the area formula.

Area = a²

Area = 13²

Area = 169.

Answer:

I am unaware of the values but the answer to this would be 256 because 8*32=256 256/32=8

Step-by-step explanation:

Answer:

256

Step-by-step explanation:

x/32=8

You must multiply to isolate the variable so you multiply 8 by 32

x=256

Let S and T denote the two finite sums,

S = 1 + x + x ² + x ³ + … + x ᴺ

T = 1 - x + x ² - x ³ + … + (-x) ᴺ

• If both S = 8 and T = 8 as N goes to infinity:

Then

xS = x + x ² + x ³ + x ⁴ + … + x ᴺ⁺¹

-xT = -x + x ² - x ³ + x ⁴ + … + (-x) ᴺ⁺¹

so that

S - xS = 1 - x ᴺ⁺¹   ==>   S = (1 - x ᴺ⁺¹)/(1 - x)

and similarly,

T = (1 - (-x) ᴺ⁺¹)/(1 + x)

For both sums, so long as |x| < 1, we have

lim [N → ∞] S = 1/(1 - x)

lim [N → ∞] T = 1/(1 + x)

Then if both sums converge to 8, this happens for

S : 1/(1 - x) = 8   ==>   x = 7/8

T : 1/(1 + x) = 8   ==>   x = -7/8

• If the sum S + T = 8 as N goes to infinity:

From the previous results, we have

1/(1 - x) + 1/(1 + x) = 8   ==>   x = ±√3/2

Hi there! :)

\(\large\boxed{\text{B. 11 cm.}}\)

Begin by using Pythagorean theorem to solve for the length of the diagonal of the base:

a² + b² = c²

Use the length and width in the equation:

8² + 3² = c²

64 + 9 = c²

73 = c²

c ≈ 8.54 cm

Now, we can find the length of the diagonal of the prism using our calculated diagonal of the base and the height. Use the same equation:

(8.54)² + 7² = c²

73 + 49 = c²

122 = c²

√122 = c

c = 11.05 ≈ 11 cm. The correct answer is B.

The formula s= ut + 1/2gt^2

Represents the total distance "s" travelled by an object in time "t" which has an initial speed of "u" and is accelerating at the uniform rate of "g". It is customary to use the symbol "g" for acceleration due to gravity. However this equation is valid for any value of uniform acceleration.

We can derive the equation as follows.

The total distance travelled by a uniformly accelerating object is equal to average speed multiplied by time

That is: s = (average speed)*t ... (1)

And, average speed = (initial speed + final speed at the end of period t)/2

And final speed = u + gt

Therefore: Average speed = (u + u + gt) = 2u + gt

Substituting this value of average speed in equation (1) we get:

s = (2u + gt)/2]*t = ut +1/2gt^2

hope it helps...!!!

The whole match lasts for 45 minutes + 45 minutes + 30 minutes = 120 minutes. Answer: 120 min.

The discriminant and the point of tangency are used to find the values of the variables as follows;

7. The line y = m·x is tangent to the curve x² + 2·x·y + 2·x = 1 when m = 1

8. The line y = 2·x - k is tangent to the curve x² + y² = 5, when k = ±5

Exercise 11.

1. The discriminant of the equation x² - 6·x + y² - 2·y + 2 = 0 is zero when y = x - 6, therefore the line x - y = 6 is tangent to the curve x² - 6·x + y² - 2·y + 2

2. The exact values of k for which the line 2·x + 3·y = k is tangent to the curve C = 4·x² + 9·y² = 36 is k = ±6·√2

The discriminant is the values which are within the radical sign of the quadratic formula.

7. At the point of tangency, the discriminant is 0

The equation is; x² + 2·x·y + 2·x = 1

The equation of the line is; y = m·x

Rewriting the equation of the curve, we get;

x² + 2·x·y + 2·x = 1

2·x·y = 1 - x² - 2·x

\(y = \dfrac{1 - x^2 - 2 \cdot x}{2\cdot x}\)

At the point of tangency, we have;

\(y = \dfrac{1 - x^2 - 2 \cdot x}{2\cdot x} = m\cdot x\)

1 - x² - 2·x - 2·m·x² = 0

1 - x² - 2·m·x² - 2·x  = 0

1 - x²·(1 - 2·m) - 2·x  = 0

The discriminant is zero at the point of tangency, which gives;

((-2²) - 4× (-(1 - 2·m)) × 1) = 0

8 - 8·m = 0

8 = 8·m

m = 8 ÷ 8 = 1

8. The line y = 2·x - k is tangent to the curve, x² + y² = 5 where we have;

y² = 5 - x²

y² = (2·x - k)²

5 - x² = (2·x - k)²

Which gives;

k² - 4·k·x + 5·x² - 5

5·x² - 4·k·x + k² - 5

At a tangent point the discriminant is therefore;

(-4·k)² - 4 × 5 × (k² - 5) = 100 - 4·k² = 0

100 - 4·k² = 0

4·k² = 100

k² = 100 ÷ 4 = 25

k = √(25) = ±5

Exercise 11

1. The equation of the line is; x - y = 6

The equation of the curve is; x² - 6·x + y² - 2·y + 2 = 0

From the equation, x - y = 6, we get; y = x - 6

Which gives; x² - 6·x + (x - 6)² - 2·(x - 6) + 2 = 0

x² - 6·x + (x - 6)² - 2·(x - 6) + 2 = 2·x² - 20·x + 50 = 0

2·x² - 20·x + 50 = 0

x² - 10·x + 25 = 0

The discriminant is; (-10)² - 4 × 1 × 25 = 0

Therefore;

3. The curve 4·x² + 9·y² = 36 has the tangent line 2·x + 3·y = k, when we have;

4·x² + 9·y² = 36

9·y² = 36 - 4·x²

y² = (36 - 4·x²)/9 = 4 - (4/9)·x²

y² = 4 - (4/9)·x²

2·x + 3·y = k

3·y = k - 2·x

y = (k - 2·x)/3

y² = ((k - 2·x)/3)²

4 - (4/9)·x² = ((k - 2·x)/3)²

4 - (4/9)·x² - ((k - 2·x)/3)² = 0

8·x² - 4·k·x + k² - 36 = 0

(-4·k)² - 4 × 8 × (k² - 36) = 0

1152 - 16·k² = 0

16·k² = 1152

k² = 1152 ÷ 16 = 72

k = √(72) = ±6·√2

Learn more about finding the tangent to a curve here:

https://brainly.com/question/22426360

#SPJ1

The current mean age of first marriage is greater than 23.3 years.

To test these hypotheses, we would need to collect current data on the age at first marriage and perform a statistical test to determine whether there is significant evidence to reject the null hypothesis in favor of the alternative hypothesis.

To investigate whether the mean age of first marriage has increased during the past 40 years, we can set up the following hypotheses:
Null hypothesis (H0):

The mean age of first marriage has not increased during the past 40 years.

In other words, the current mean age of first marriage is still 23.3 years.
H0: μ = 23.3
Alternative hypothesis (H1): The mean age of first marriage has increased during the past 40 years.

In other words, the current mean age of first marriage is greater than 23.3 years.
H1: μ > 23.3

For similar question on hypotheses.

https://brainly.com/question/11555274

#SPJ11

Answer:

1) 30 pounds is the weight of the bag all together

2) science book is the heaviest book

Step-by-step explanation:

bag=4 pounds

library book=2 pounds

maths book=2×4=8 pounds

science book=8×2=16 pounds

4+2+8+16=30 pounds all together

heaviest book= science book (16 pounds)

Answer:

The common difference in the given sequence is 5.

Step-by-step explanation:

The common difference in the sequence is 5 because they all add by 5 each time for example 5 + 5= 10 and 10+5=15

An exponential equation in the form \(y=a(b)^x\) that can model the amount of caffeine, y, in Kendall's body x hours after drinking the coffee is

The amount of caffeine that will be in Kendall's body after 12 hours is 18 milligrams.

In Mathematics, an exponential function can be modeled by using the following mathematical equation:

f(x) = a(b)^x

Where:

Since Kendall drank a cup of coffee that had 95 milligrams of caffeine which is decreasing at a rate of 5% per day, this ultimately implies that the relationship is geometric and the rate of change (decay rate) is given by:

Rate of change (decay rate) = 100 - 13 = 87% = 0.87.

By substituting the parameters into the exponential equation, we have the following;

\(f(x) = 95(0.87)^x\)

When x = 12, we have;

\(f(12) = 95(0.87)^{12}\)

f(12) = 17.86 ≈ 18 milligrams.

Read more on exponential equation here: brainly.com/question/28939171

#SPJ1

Answer:

B: 1.53

Step-by-step explanation:

The mean, or average, is 4, and n, the amount of numbers, is 7. To find the standard deviation, first, all of the numbers are subtracted by the mean. This makes (-3, 0, 0, 0, 0, 1, 2). Square all of them to get (9, 0, 0, 0, 0, 1, 4). Next add the squared numbers together (9 + 0 + 0 + 0 + 0 + 1 + 4 = 14). Next, the variance needs to be found. That is found by this formula: (Sum of previous number set ÷ (n - 1)). So in this case, (14 ÷ (n - 1)). Since n is 7, it is (14 ÷ (7 - 1)), or (14 ÷ 6). The answer to that is 2.3 repeating. After the variance is found, it is square rooted to get the standard deviation. √2.3 is about 1.53. Hope this helps! Have a great day! :)

Answer:

x=18.9

Step-by-step explanation:

Answer: 15 years old

Step-by-step explanation:

maria is 15 , selena is 17 , and sophia is 12

Answer: 2 3/4 > 2.68 is correct (only)

Step-by-step explanation: 2 3/4 = 2.75, and 2.75 is greater than 2.68

The rest are incorrect. 7.895 * 10^2 (100) = 789.5, and 5.43 * 10^3 (1000) = 5430. So 789.5 > 5430 is false.

Sqrt(63) = 7.93, and 7.93 > 8.11 is false.

Absolute values ( | | ) mean that no matter if it is negative or positive, it will become positive (unless the negative sign is outside the absolute value). 1.5 > 3.2 is false, and even without the absolute value, -1.5 is still less than 3.2

The solutions to the equation √( x + x² ) = 0 are x = 0 and x = -1.

Given equation in the question;

√( x + x² ) = 0

First, remove the radical of the left side of the equation by squaring both sides.

(√( x + x² ))² = 0²

x + x² = 0²

x + x² = 0

Next, factor the left side of the equation.

The common factor between x and x² is x

x( 1 + x ) = 0

Hence

x = 0

1 + x = 0

Subtract 1 from both sides

1 - 1 + x = 0 - 1

x = 0 - 1

x = -1

Therefore, the values of x are 0 and -1.

Learn more about quadratic equation here: https://brainly.com/question/4038687

#SPJ1

Both of the intervals given are meaningful intervals in mathematics, but they are different types of intervals.Therefore, the interval (1, -13] is meaningless because it does not contain any real numbers.

An interval is a number or range of values ​​between two endpoints. 

The endpoints can be included or excluded from the interval, and the interval can be open, closed, or half-open depending on whether the endpoints are included or excluded.

The interval (-12, 0] is a closed interval, which includes the endpoint 0, and all real numbers between -12 and 0.

The square bracket indicates that the endpoint 0 is included in the interval.

The interval (1, -13] is an empty interval, which includes no real numbers, since there is no number that is greater than 1 and less than or equal to -13. This interval is meaningless because it does not contain any numbers.

To know more about real numbers visit:

https://brainly.com/question/29109826

#SPJ1

Answer:

Create equivalent expressions in the equation that all have equal bases, then solve for  

x

.

Exact Form:

5/3

Decimal Form:

x

=

1.6

Mixed Number Form:

x

=

1  2/3

Answer:-3

Step-by-step explanation:

Answer:

5

Step-by-step explanation:

Divide both sides by 2.

Answer:

x=5

Step-by-step explanation:

2x=10

Divide 2 from the other side to isolate the variable.

x=5

Answer:

Eso es incorrecto 550 es mayor por solamente 50 numeros

Step-by-step explanation:

Answer:

f(x) = x³ - 4x + 6

f'(x) = 3x² - 4

a) f'(2) = 3(2²) - 4 = 12 - 4 = 8

6 = 8(2) + b

6 = 16 + b

b = -10

y = 8x - 10

b) 3x² - 4 = 0

3x² = 4, so x = ±2/√3 = ±(2/3)√3

= ±1.1547

f(-(2/3)√3) = 9.0792

f((2/3)√3) = 2.9208

c) 3x² - 4 = 8

3x² = 12

x² = 4, so x = ±2

f(-2) = (-2)³ - 4(-2) + 6 = -8 + 8 + 6 = 6

6 = -2(8) + b

6 = -16 + b

b = 22

y = 8x + 22

f(2) = 6

y = 8x - 10

The equation perpendicular to the tangent is y = -1/8x + 25/4

-The smallest slope on the curve is 2.92

The curve has the smallest slope at the point (1.15, 2.92)

The equations at tangent points are y = 8x + 16 and  y = 8x - 16

From the question, we have the following parameters that can be used in our computation:

y = x³ - 4x + 6

Differentiate

So, we have

f'(x) = 3x² - 4

The point is (2, 6)

So, we have

f'(2) = 3(2)² - 4

f'(2) = 8

The slope of the perpendicular line is

Slope = -1/8

So, we have

y = -1/8(x - 2) + 6

y = -1/8x + 25/4

We have

f'(x) = 3x² - 4

Set to 0

3x² - 4 = 0

Solve for x

x = √[4/3]

x = 1.15

So, we have

Smallest slope = (√[4/3])³ - 4(√[4/3]) + 6

Smallest slope = 2.92

So, the smallest slope is 2.92 at (1.15, 2.92)

Here, we set f'(x) to 8

3x² - 4 = 8

Solve for x

x = ±2

Calculate y at x = ±2

y = (-2)³ - 4(-2) + 6 = 6: (-2, 0)

y = (2)³ - 4(2) + 6 = 6: (2, 0)

The equations at these points are

y = 8x + 16

y = 8x - 16

Read more about tangent lines at

https://brainly.com/question/21595470

#SPJ1

9,513 rounded off to nearest thousands = 10,000

we have given a four digit number 9,513 to round off to nearest thousands.

steps that should be followed for rounding numbers to the nearest thousand:

round 9,513 to nearest thousands:

∵ hundreds place is 5

∴9,513≈10,000

hence, 9,513 nearest thousands is 10,000

learn more about rounding  here brainly.com/question/15265892

#SPJ9