Work out the size of angle x in the hexagon
below.
124°
110°
141°
130°
X
70°
Not drawn accurately

Answers
The size of angle x in the hexagon is 486 degrees.
To find the size of angle x in the hexagon, we need to use the fact that the sum of the interior angles of a hexagon is always 720 degrees.
In a regular hexagon, all the interior angles are congruent, so we can divide 720 by 6 to find the measure of each angle.
720 degrees / 6 = 120 degrees
However, in the given hexagon, we have an angle measuring 124 degrees and an angle measuring 110 degrees. To find the size of angle x, we need to subtract the sum of these two angles from the total sum of interior angles of a hexagon (720 degrees).
720 degrees - 124 degrees - 110 degrees = 486 degrees
As a result, angle x in the hexagon has a size of 486 degrees.
for such more question on hexagon
https://brainly.com/question/23875717
#SPJ8
Related Questions
Here is the graph of the function y = f(x).
Graph the function \(y=\frac{1}{3} f(x-4)-2\)
![Here is the graph of the function y = f(x).Graph the function [tex]y=\frac{1}{3} f(x-4)-2[/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/FmFa6wju0eDhD5p9U9lVzQnEyR3scJtx.png)
Answers
Answer:
See attached graph----------------------------
The graph of f(x) shows the vertex at (3, 2)
Its equation isf(x) = (x - 3)² + 2The function g(x) = 1/3f(x - 4) - 2 isg(x) = 1/3[(x - 3 - 4)² + 2] - 2 = 1/3[(x - 7)² + 2] - 2 =1/3(x - 7)² + 2/3 - 2 =1/3(x - 7)² - 4/3![Here is the graph of the function y = f(x).Graph the function [tex]y=\frac{1}{3} f(x-4)-2[/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/VgwJV52fDPtezalGVATmNY2wPJC9p1hn.png)
Solve x - 19 < 81
hurry bestie
Answers
Answer:
x < 100
Step-by-step explanation:
x - 19 < 81
* add 19 to each side *
- 19 + 19 cancels out
81 + 19 = 100
x < 100
Help yalll I really need help major time

Answers
Answer:
Annalise is correct because the outputs are closest when x = 1.35
Step-by-step explanation:
The solution to the equation 1/(x-1) = x² + 1 means the one x value that will make both sides equal. If we look at the table, notice how when x = 1.35, f(x) values are closest to each other for both equations, signifying that x = 1.35 is approximately the solution. Thus, Annalise is correct.
Here is a table of values for y = f(x).
X -2 -1 0 1 2 3 4 5 6
f(x) 5 6 7 8 9 10 11 12 13
Mark the statements that are true.

Answers
Answer:
a, b, and d are all correct
im 99% sure
Step-by-step explanation:
help without guessing

Answers
Answer:
Step-by-step explanation:
A. There is a ± to show that there are 2 possible answers
Ex:
x²=16
x can be 4 or -4 for this statement to be true.
3. Proportion Test Currently, the conversion rate of the advertisement campaign is 1.5%. The conversion rate is the number of conversions (i.e., sales) divided by the total number of clicks. A new advertisement campaign has been proposed and studied. A sample of 10,000 customers clicked the new advertisement and 163 of them purchased the product. Do the results of this study support the claim that the new advertisement campaign is more effective than the current advertisement
Answers
The proportion test can be used to determine whether the new advertisement campaign is more effective than the current advertisement campaign or not. The current conversion rate of the advertisement campaign is 1.5%. The results of this study support the claim that the new advertisement campaign is more effective than the current advertisement campaign.
In other words, out of the total clicks, 1.5% of the customers purchase the product. Now, a new advertisement campaign has been proposed and studied. A sample of 10,000 customers clicked the new advertisement and 163 of them purchased the product.
To determine whether the new advertisement campaign is more effective than the current advertisement campaign or not, we need to test the following null and alternative hypothesis:
Null hypothesis (H0): The new advertisement campaign is not more effective than the current advertisement campaign.
Alternative hypothesis (H1): The new advertisement campaign is more effective than the current advertisement campaign.
Now, we can calculate the sample proportion as follows:
\(p = x/n\)
where x is the number of successes (i.e., customers who purchased the product) and n is the sample size (i.e., total number of clicks).
In this case,
p = 163/10,000 = 0.0163
Now, we can calculate the test statistic (Z-score) as follows:
Z = (p - P) / √(P(1 - P) / n)
where P is the proportion under the null hypothesis. In this case, P = 0.015.
Z = (0.0163 - 0.015) / √(0.015(1 - 0.015) / 10,000)
Z = 2.21
The p-value for this test is 0.0136.
Since the p-value is less than the significance level (α = 0.05), we reject the null hypothesis and conclude that the new advertisement campaign is more effective than the current advertisement campaign. Therefore, the results of this study support the claim that the new advertisement campaign is more effective than the current advertisement campaign.
To learn more about advertisement visit;
https://brainly.com/question/32251098
#SPJ11
There were 24 1/4 crates of tomatoes in the barn but 7 3/5 crates of tomatoes were rotten and had to be thrown out. Joe sold 8 1/3 crates and canned 7 5/6 crates of tomatoes. How many crates of tomatoes were left?
Answers
Answer:
29/60 of the crates are left behind.
Step-by-step explanation:
Total number of crates = 24 1/4= 97/4
Rotten tomatoes crates = 7 3/5= 38/5
Joe sold crates = 8 1/3= 25/8
Canned crates of tomatoes =7 5/6= 47/6
Therefore
24 1/4 - 7 3/5 - 8 1/3 - 7 5/6
= 97/4-38/5-25/3-47/6
= (97*5-38*4)/20 - (25*2+47)/6
= 485-152/20 - 97/6
= 333/20-97/6
= 333*3-97*10/60
=999-970/60
=29/60
29/60 of the crates are left behind.
This question is solved in 2 steps.
First the LCM of fraction 1 and 2 is taken separately from the LCM of fraction 3 and 4 for simplification purposes.
Then again the LCM is taken for the answers obtained from fraction 1&2 and fraction 3& 4.
Factor by grouping.
64p2 – 48p – 27
(8p – 9)(8p – 3)
(8p – 9)(8p + 3)
(8p + 9)(8p + 3)
(8p + 9)(8p – 3)
Answers
Answer:
B
Step-by-step explanation:
hope this helps with the work
Please help me!!! I need soooo much help

Answers
Answer: option 3
Step-by-step explanation:
Find the perimeter of a polygon. Assume that lines which appear to be tangent are tangent
A. 32.1
B. 39
C. 45.2
D. 59.7

Answers
Answer:
(C). 45.2
Step-by-step explanation:

The transformation which will map triangle PQR onto P'Q'R is

Answers
Given:
The graph of triangle PQR and triangle P'Q'R'.
To find:
The transformation that will map the triangle PQR onto P'Q'R'.
Solution:
From the given graph it is clear that the triangle PQR is formed in II quadrant and its base lies on the negative direction of x-axis.
The triangle P'Q'R' is formed in IV quadrant and its base lies on the positive direction of x-axis.
This is possible it the figure is rotated 180 degrees about the origin.
Therefore, the correct option is A.
Hi, can anyone help me with this. I'm really confused lol

Answers
Answer:
X=8
Step-by-step explanation:
since we know these lines are parallel that means that the 2 angels given to us are supplementary (add up to 180) so we add them together and set it equal to 180 to find X.
what is the approximate average rate at which the area decreases, as the rectangle's length goes from 13\text{ cm}13 cm13, start text, space, c, m, end text to 16\text{ cm}16 cm16, start text, space, c, m, end text?
Answers
The approximate average rate at which the area decreases as the rectangle's length goes from 13 cm to 16 cm is equal to the width (w) of the rectangle.
To determine the approximate average rate at which the area decreases as the rectangle's length goes from 13 cm to 16 cm, we need to calculate the change in area and divide it by the change in length.
Let's denote the length of the rectangle as L (in cm) and the corresponding area as A (in square cm).
Given that the initial length is 13 cm and the final length is 16 cm, we can calculate the change in length as follows:
Change in length = Final length - Initial length
= 16 cm - 13 cm
= 3 cm
Now, let's consider the formula for the area of a rectangle:
A = Length × Width
Since we are interested in the rate at which the area decreases, we can consider the width as a constant. Let's assume the width is w cm.
The initial area (A1) when the length is 13 cm is:
A1 = 13 cm × w
Similarly, the final area (A2) when the length is 16 cm is:
A2 = 16 cm × w
The change in area can be calculated as:
Change in area = A2 - A1
= (16 cm × w) - (13 cm × w)
= 3 cm × w
Finally, to find the approximate average rate at which the area decreases, we divide the change in area by the change in length:
Average rate of area decrease = Change in area / Change in length
= (3 cm × w) / 3 cm
= w
Therefore, the approximate average rate at which the area decreases as the rectangle's length goes from 13 cm to 16 cm is equal to the width (w) of the rectangle.
learn more about rectangle here
https://brainly.com/question/15019502
#SPJ11
Una caja grande cuesta lo mismo que tres pequeñas. Si 7 cajas grandes y 4 pequeñas cuestan $12 más que 4 grandes y 7 pequeñas ¿Cuál es el sistema de ecuaciones que modela el sistema?
Answers
Answer:
\( x = 3y \)
\(7x+4y= 12 + 4x+7y\)
Step-by-step explanation:
Para resolver la pregunta, basta con definir variables adecuadas y traducir cada relación. Sea x el costo de una caja grande e y el costo de una caja pequeña. Tenemos que el costo de una caja grande es igual a 3 cajas pequeñas. Es decir, x = 3y. Luego, tenemos que
\(7x+4y= 12 + 4x+7y\)
pues al sumarle 12 al costo de 4grande y 7 pequeñas obtenemos el costo de 7 grande y cuatro pequeñas. De aquí, el sistema de ecuaciones que modela el sistema es
\( x = 3y \)
\(7x+4y= 12 + 4x+7y\)
Question in image. :)

Answers
Answer:
All real numbers greater than or equal to 0.
General Formulas and Concepts:
Algebra I
Domain is the set of x-values that can be inputted into function f(x)Step-by-step explanation:
According to the graph, we see that our x-values span from 0 to infinity. Since 0 is a closed dot, it is inclusive in the domain:
[0, ∞) or x ≥ 0 or All Real Numbers greater than or equal to 0.
a grain silo consists of a cylindrical main section and a hemispherical roof of the total volume of the silo (including the part inside the roof section) is 10,000 find.the.cylindrical part is 30 ft tall, what is the radius of the silo, correct to the nearest tenth of a foot?
Answers
The radius of the silo which is in the shape of cylinders and spheres , correct to the nearest tenth of a foot, is approximately 10.3 feet.
To find the radius of the silo, we need to determine the radius of the cylindrical section.
The volume of the cylindrical section can be calculated using the formula:
\(V_{cylinder} = \pi * r^2 * h\)
where \(V_{cylinder}\) is the volume of the cylindrical section, r is the radius of the cylindrical section, and h is the height of the cylindrical section.
Given that the cylindrical section is 30 ft tall, we can rewrite the formula as:
\(V_{cylinder} = \pi * r^2 * 30\)
To find the radius, we can rearrange the formula:
\(r^2 = V_{cylinder} / (\pi * 30)\)
Now, we can substitute the total volume of the silo, which is 10,000 cubic feet, and solve for the radius:
\(r^2 = 10,000 / (\pi * 30)\)
Simplifying further:
\(r^2 = 106.103\)
Taking the square root of both sides, we find:
\(r = \sqrt{106.103} = 10.3\)
Therefore, the radius of the silo which is in the shape of cylinders and spheres , correct to the nearest tenth of a foot, is approximately 10.3 feet.
Learn more about cylinders and spheres here.
https://brainly.com/question/23947152
#SPJ4
How many sides does a polygon have if the sum of the interior angles is 900
Answers
Answer:
there are 7 sides.
Step-by-step explanation:
hope this helped you
Answer:
7
Step-by-step explanation:
n: number of sides
900 = (n-2)180
900 = 180n - 360 Add 360 to both sides
1260 = 180n Simplify
n = 7
If y = sin - (x), then y' = = d dx [sin - (x)] 1 – x2 This problem will walk you through the steps of calculating the derivative. (a) Use the definition of inverse to rewrite the given equation with x as a function of y. sin(y) = x Oo Part 2 of 4 (b) Differentiate implicitly, with respect to x, to obtain the equation.
Answers
To rewrite the given equation with x as a function of y, we use the definition of inverse. x = sin^(-1)(y).
To obtain the inverse of a function, we interchange the roles of x and y and solve for x. In this case, we have y = sin(x), so we swap x and y to get \(x = sin^(-1)(y), where sin^(-1)\)denotes the inverse sine function or arcsine.
To differentiate implicitly with respect to x, we start with the equation y = sin(x) and differentiate both sides with respect to x. The derivative of y with respect to x is denoted as y', and the derivative of sin(x) with respect to x is cos(x). Therefore, the equation becomes:
dy/dx = cos(x).
Implicit differentiation allows us to find the derivative of a function when the dependent variable is not explicitly expressed in terms of the independent variable. In this case, we differentiate both sides of the equation with respect to x, treating y as a function of x and using the chain rule to differentiate sin(x). The resulting derivative is\(dy/dx = cos(x).\)
learn more about sine function here
https://brainly.com/question/26020087
#SPJ11
5) x-y+6; use x = 6, and y = 1
Answers
Answer:
-1
Step-by-step explanation:
substitute x for 6 and y for 1
which will be 6-1+6
using BODMAS
6-(1+6)
6-7= -1
65/1000 as a percent tysm
Answers
Answer:
6.5%
Step-by-step explanation:
Hope that helped! =)
Since the bottom number is in the thousands that is why the percent is smaller. and since 65/100 will represent that in the hundredths the bigger the bottom number, just know the top number of it no matter if it is a 75 or 86 it will always be smaller.
PLS HELP SOON I GUESS

Answers
Answer:
the answer is -2 if you look at the left side of the graph and were the line is at you will see that the number goes through -2.
1) 35 is what percent of 140 2) 250 is 45% of what number? 3) 74 is what percent of 740? 4) 350 is 50% of what number?
Answers
Answer:
1) 25%
2) 555.56
3) 10%
4) 700
Step-by-step explanation:
1) 35 is what percent of 140
This is calculated as:
35/140 × 100
= 25%
2) 250 is 45% of what number?
Let the number be represented as x
This is calculated as:
45% of x = 250
45/100 × x = 250
45x /100 = 250
Cross Multiply
45x = 250 × 100
x = 25000/45
x = 555.55555556
x = 555.56
3) 74 is what percent of 740?
Let the percentage be represented by x
x% × 740 = 74
Divide both side by 740
x% = 74/740
x% = 0.1
Converting to percentage
0.1 × 100 = 10%
4) 350 is 50% of what number?
Let the number the represented by x
This is calculated as:
50% of x = 350
50/100 × x = 350
50x /100 = 350
Cross Multiply
50x = 350 × 100
x = 35000/50
x = 700
x = 555.56
Help asap pleaseee answere it separately
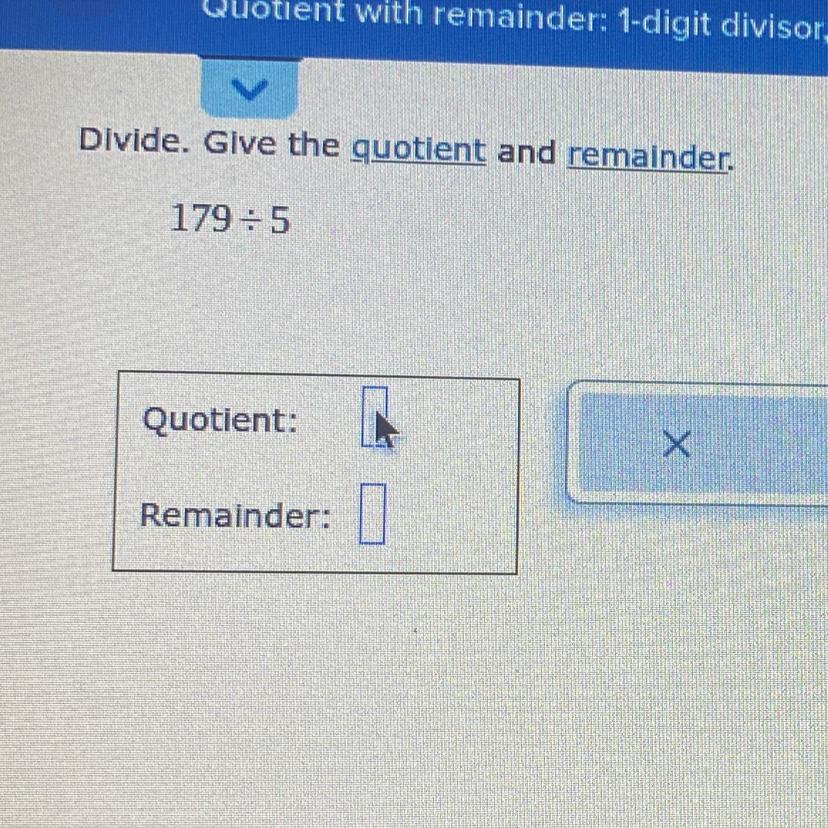
Answers
Answer:
179 divided by 5 equals 35 with a remainder of 4.
Quotient: 35
Remainder: 4
7+
3 points
Which expression is equivalent to -15x + 39?
A
-3 (5x – 13)
B
-3 (5x + 13)
C
3 (5x – 13)
D
3(5x + 13)

Answers
(-3)(5x+-13)
=(-3)(5x)+(-3)(-13)
So your answer should be A. -15x+36
Hope this helps ❤️
The order is for Colace liquid 100mg bid. You have Colace liquid 25mg/5ml. How much will you administer? 8. There are 1000mg in 1 gram. How many grams is 567mg ? grams (round to the hundredth) 9. The patient weighs 184lbs. What is this patient's weight in kilograms? 10. The physician orders Phenobarbital elixir (liquid) 60mg PO bid. You have Phenobarbital elixir 30mg per 5ml. How many ml will you administer? Round the following numbers to the HUNDREDTH. 1. 5.2567 2. 3.33455 3. 2.4555555 4. 125.36211 5. 12.31567 6. There are 30 mL to every 1 ounce of liquid. You drank 8 ounces of orange juice; how many mL of orange juice did you drink? mL of orange juice. 7. There are 5 mL in every teaspoon. The recipe you are making is in metric and calls for 15ml of baking powder. How many teaspoons of baking powder do you need?
Answers
The quantity of teaspoons needed will be 3 teaspoons of baking powder.
There are 1000mg in 1 gram.
Therefore, 567mg will be equal to 0.567g.
The formula for converting weight from pounds to kilograms is to divide the weight in pounds by 2.2.
Therefore, the patient's weight in kilograms will be equal to: 184 lbs ÷ 2.2 = 83.6364 kg.
The physician orders Phenobarbital elixir (liquid) 60mg PO bid.
You have Phenobarbital elixir 30mg per 5ml.
Therefore, the quantity of ml to be administered will be:60mg ÷ 30mg/5ml = 2ml.
15.2567 rounded to the nearest hundredth is 5.26
3.33455 rounded to the nearest hundredth is 3.33
2.4555555 rounded to the nearest hundredth is 2.466
125.36211 rounded to the nearest hundredth is 125.366
12.31567 rounded to the nearest hundredth is 12.316.
There are 30 mL to every 1 ounce of liquid.
Therefore, if 8 ounces of orange juice are consumed, the total quantity of ml of orange juice will be: 8 oz × 30 mL/oz = 240 mL.7.
There are 5 mL in every teaspoon. The recipe you are making is in metric and calls for 15ml of baking powder.
Therefore,15 ml ÷ 5 ml/teaspoon = 3 tablespoons of baking powder will be required for the recipe.
learn more about quantity from given link
https://brainly.com/question/13014675
#SPJ11
assume that the salries of elementary schoool teahcers ina particular country are normally distributed witha mean of 38000 and a standard deviation of 4000
Answers
The cutoff salary for teachers in the top 10% is approximately $43,120.
Since the salaries are normally distributed, we can use z-scores to find the cutoff point. The z-score represents the number of standard deviations a data point is from the mean. We can use the z-score formula:
z = (x - μ) / σ
Where:
z is the z-score
x is the cutoff salary we want to find
μ is the mean salary
σ is the standard deviation
We want to find the z-score that corresponds to the top 10% of salaries, which means we need to find the z-score that corresponds to the cumulative probability of 0.90 (1 - 0.10) from the standard normal distribution.
Using a standard normal distribution table or calculator, we can find that the z-score for a cumulative probability of 0.90 is approximately 1.28.
Now, we can rearrange the z-score formula to solve for x:
z = (x - μ) / σ
Rearranging:
x = μ + z * σ
Plugging in the values:
x = $38,000 + 1.28 * $4,000
Calculating:
x ≈ $38,000 + $5,120
x ≈ $43,120
learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
COMPLETE QUESTION :
Assume that the salaries of elementary school teachers in a particular country are normally distributed with a mean of $38,000 and a standard deviation of $4,000. What is the cutoff salary for teachers in the top 10%?
what is the slope of the line and y intercept pls help

Answers
Answer:
the answer would be B
Step-by-step explanation:
for the slope you would need to count up then over between the two points and do that until you reach where the line crosses or in this case would cross for the y-intercept
if Sₙ is the nth partial sum of the infinite series [infinity]∑ₙ₌₁ aₙ , and n>3 , which of the following is true?
a. aₙ = Sₙ₋₁ - Sₙ₋₂
b. aₙ = Sn - Sₙ₋₁
c. aₙ = Sₙ₊₁ - Sₙ
d. aₙ = Sₙ₊₁ - Sₙ₋₁
Answers
The correct statement is option (d): aₙ = Sₙ₊₁ - Sₙ₋₁. The nth partial sum, Sₙ, represents the sum of the first n terms of the infinite series ∑ₙ₌₁ aₙ. We are given that n > 3.
To determine the relationship between the nth term, aₙ, and the partial sums, we can examine the pattern of the series. Looking at the options, we observe that option (d) is the difference between Sₙ₊₁ and Sₙ₋₁.
Let's consider an example to understand why this is the correct choice. Suppose we have the series 1 + 2 + 3 + 4 + 5 + ... and we want to find the relationship between the terms and the partial sums. The partial sums would be 1, 3, 6, 10, 15, ... We can see that the difference between consecutive partial sums is 2, 3, 4, 5, ... which corresponds to the terms of the series. Thus, aₙ = Sₙ₊₁ - Sₙ₋₁.
In general, for any infinite series with n > 3, the correct relationship between the nth term, aₙ, and the partial sums, Sₙ, is given by aₙ = Sₙ₊₁ - Sₙ₋₁, which is option (d).
Learn more about series here: https://brainly.com/question/30601985
#SPJ11
If the number of bacteria on the surface of your phone triples every hour and can be described by the exponential function: f(x)=1000x3^x
, complete the table of values to show how much bacteria is on your phone after 4 hours.

Answers
Answer: 81,000
Step-by-step explanation:
We can solve this by using the formula given.
If f(1)=1000x3^1, then 1,000x3=3,000
If f(2)=1000x3^2, then 3^2=9 and 1000x9=9000,
and so on,
Now, f(4) will equal 1000x3^4, and 3^4 is 3x3x3x3, which is 9x9 or 9^2, which would be equal to 81, and 81x1000=81,000
To complete the table of values for the exponential function f(x) = 1000*3^x, we can evaluate the function for x = 0, 1, 2, 3, and 4, since we are interested in the number of bacteria on the phone after 4 hours.
x f(x)
0 1000
1 3000
2 9000
3 27,000
4 81,000
Therefore, after 4 hours, there will be 81,000 bacteria on the surface of the phone, assuming the number of bacteria triples every hour and can be described by the exponential function f(x) = 1000*3^x.
#SPJ1
Let AB // ED , AB = 10 units, AC = 12 units, and DE = 5 units. What is the length of AD?

Answers
Answer:
length of CD = 18 units.
Step-by-step explanation:
In ΔABC and ΔCED,
AB║DE and AD is a transversal line,
m∠ABC = m∠CED [Alternate interior angles]
m∠ACB = m∠DCE [Vertically opposite angles]
ΔABC ~ ΔCED [By AA property of similarity]
Therefore, by the property of similar triangles, corresponding sides will be proportional.
\(\frac{AB}{DE}= \frac{AC}{DC}\)
\(\frac{10}{5}=\frac{12}{CD}\)
CD = 6
Since, AD = AC + CD
AD = 12 + 6
= 18 units
Therefore, length of CD = 18 units.