Write an equation of a line with the given slope and y-intercept.
m = -2,b=4
Answers
Answer:
\(y = -2x+4\)
Step-by-step explanation:
Linear equations can be written in the form \(y=mx+b\) where \(m\) is the gradient/slope and \(b\) is the y-intercept of the line.
With the given slope and y-intercept, the linear equation of the line can be written as \(y=-2x+4\).
Related Questions
Graph the inequality.
-73y + 2x <14
Answers
x=-8 All the values less than 7 are included in the number line. The graph on number line is shown in figure attached. In the options given
a recipe for cookies calls for 2/3 of a cup of sugar per batch. elena used 6 2/3 cups of sugar to make multiple bathes did she make
Answers
Answer:
Elena made 10 batches.
Step-by-step explanation:
1 batch uses 2/3 cup
Elena used 6 2/3 cup
The number of batches is the quotient of 6 2/3 and 2/3.
We need to divide 6 2/3 by 2/3. First, we convert 6 2/3 into a fraction.
6 2/3 ÷ 2/3 = 20/3 ÷ 2/3 = 20/3 × 3/2 = 10
Answer: Elena made 10 batches.
Answer:
10
Step-by-step explanation:
2/3 for 1 cup if he used 6 2/3 of sugar then its 10.
if you times 2/3 by 10 its 6.66 and 6.66 is 2/3
1/3=33
2/3=66
3/3=100
Someone help me pleaseeee

Answers
For the given right triangle, L = 66°, LK = 3.56, and the hypotenuse, LM = 8.75.
What is right triangle?A right triangle, right-angled triangle, or more formally an orthogonal triangle—previously known as a rectangled triangle—is a triangle with one angle that is a right angle (i.e., a 90-degree angle), meaning that two of its sides are perpendicular. The foundation of trigonometry is the relationship between the sides and other angles of a right triangle.
The hypotenuse is the side that faces the right angle (side c in the figure). Legs are the sides that are next to the right angle (or catheti, singular: cathetus). Side a can be thought of as the side that is adjacent to angle B and opposite to (or opposite) angle A, whereas side b is the side that is adjacent to angle A and opposite to angle B.
Given a right triangle with base = 8 and an angle = 24°
Using angle sum property of triangle
24 + 90 + angle L = 180
L = 66°
Using Sohcahtoa
Tangent: tan(θ) = Opposite / Adjacent
tan(24°) = LK/8
0.445 = LK/8
LH = 8 × 0.445
LK = 3.56
LM = \(\sqrt{MK^2 + LK^2}\)
LM = \(\sqrt{8^2 + 3.56^2}\)
LM = 8.75
Thus, For the given right triangle, L = 66°, LK = 3.56, and the hypotenuse, LM = 8.75.
Learn more about right triangle
https://brainly.com/question/4364353
#SPJ1
Titan put $3,400 in a savings account at a local bank. The bank will pay him 1.9% annual simple interest. How much interest will Titan earn after 4 years?
Answers
Answer: $258.40
Step-by-step explanation:
The formula to calculate the simple interest will be:.
= Principal × Rate × Time
where,
Principal = $3400
Rate = 1.9%
Time = 4
Interest = $3400 × 1.9% × 4
= $3400 × 0.019 × 4
= $258.40
in a bag of marbles, 1 2 are red, 1 4 are blue, 1 6 are green, and 1 12 are yellow. you pick a marble without looking. what color marble are you most likely to choose?
Answers
write an inequality representing I, the number of outfits she can buy while staying within her budget

Answers
Anna has $540 to spend at the bicycle shop → this means that she can spend the $540 or less, you can symbolize this as ≤ $540
Her costs include:
• A bicycle for ,$402.87
,• 3 bicycle reflectors for $10.97/each, the total will be 3*10.97=,$32.91
,• A pair of bike gloves for ,$14.42
,• With the remaining money, she wants to buy as many biking outfits as possible. Let "o" represent the number of outfits she can buy, considering each one costs $44.90, then the total cost for the outfits can be symbolized as ,$44.90o
The calculation for her total expenses is the sum of everything she buys:
"Bicycle"+"Reflectors"+"Gloves"+"Outfits"≤$540
Using the costs listed above the expression is
\(402.87+32.91+14.42+44.90o\leq540\)Simplify the like terms, i.e. add the alone numbers together
\(450.20+44.90o\leq540\)what is the ratio of the circumstance to the diameter

Answers
Answer:
3.14
Step-by-step explanation:
110/35=3.14
How much is a 25% tip on a meal costing $44.00 ?
Answers
Answer:
$11
Step-by-step explanation:
44 x 0.25 = 11
please compare the lotka integral equation and the mckendrick-von foerster model. are they based on the same assumptions? how these models are related? how these models are different?
Answers
The Lotka integral equation and the McKendrick-von Foerster model are distinct mathematical models for studying population dynamics.
The Lotka integral equation describes the growth of a single-species population and incorporates an integral term to represent the accumulated growth.
The McKendrick-von Foerster model focuses on age-structured populations and does not explicitly contain an integral term but can incorporate it for age-dependent processes.
The Lotka integral equation and the McKendrick-von Foerster model are both mathematical models used in population dynamics. While they share similarities, they are based on different assumptions and have distinct characteristics. In this explanation, we will explore the relationship between these two models and highlight their similarities and differences.
The Lotka integral equation considers a single-species population and assumes exponential growth with a declining growth rate as resources become limited. It explicitly incorporates an integral term, representing accumulated growth over time.
On the other hand, the McKendrick-von Foerster model focuses on age-structured populations, considering the transitions between different age classes. While it does not explicitly contain an integral term, it can accommodate integral components if age-dependent processes are included.
To know more about integral here
https://brainly.com/question/18125359
#SPJ4
what is size for tv?
Answers
The size for a TV is determined as the diagonal length of the Television.
The Televisions that we see in our daily life are mostly of the rectangular shape.
A rectangular shape is a shape that has 4 sides in it, the opposite sides of the rectangular are parallel and equal. Two pairs of equal sides are formed in this type of shape.
If we connect the vertices that are directly opposite to each other than it is known as the diagonal of the rectangle . Often we see that the TV is of 32'' or 64''. This only means that the diagonal length of the TV is 32'' or 64''. This is how we measure the size of the TV.
To know more about diagonal, visit,
https://brainly.com/question/27341413
#SPJ4
The diagram below represent the rate of making copies on a copy machine. Which table represent this rate?

Answers
Answer:
its B
Step-by-step explanation:
How will you describe the graph of exponential function?
Answers
The graph of exponential function, is described below.
What is an exponential function?
The mathematical formula f(x) = e^x stands for the exponential function. The term, unless specifically stated otherwise, generally refers to the positive-valued function of a real variable, though it can be extended to the complex numbers or generalized to other mathematical objects like matrices or Lie algebras.
The formula for an exponential growth function is y = ab^x, where a > 0 and b > 1. As can be seen in the example of f(x) = 2x below, the graph will ascend. The numbers get smaller as x gets closer to negative infinity, as you can see.
If b > 1 , then the graph's slope is positive and exponential growth is depicted. The value of y approaches infinity as x rises. The value of y approaches zero as x falls.
To know more about exponential function, click on the link
https://brainly.com/question/2456547
#SPJ4
Bindu's Drama class is performing a play. She wants to buy as many tickets as she can afford. If tickets cost
$3,25 each and she has $14.75 to spend, how many tickets can she buy?
Answers
Answer:
4 tickets
Step-by-step explanation:
3.25 x 4 = 13
She can afford 4 tickets and have 1.75 $ left over.
hopefully this helps you :)
pls mark brainlest ;)
If 43% of American pet owners keep a photograph of their pet in their wallet, find the probability that 5 randomly selected American pet owners will have a photograph of their pet in their wallet. Please round the final answer to 2 or 3 decimal places.
Answers
To find the probability that 5 randomly selected American pet owners will have a photograph of their pet in their wallet, we can use the binomial probability formula.
The binomial probability formula is given by:
\(P(X = k) = C(n, k) * p^k * (1 - p)^(n - k)\)
Where:
P(X = k) is the probability of exactly k successes,
n is the number of trials,
k is the number of successful outcomes,
p is the probability of success on a single trial.
In this case:
n = 5 (5 randomly selected pet owners)
k = 5 (the number of pet owners with a photograph of their pet)
p = 0.43 (the probability of a pet owner having a photograph)
Using the formula:
\(P(X = 5) = C(5, 5) * 0.43^5 * (1 - 0.43)^(5 - 5)\)
C(5, 5) = 1 (since there is only one way to choose 5 out of 5)
\(P(X = 5) = 1 * 0.43^5 * (1 - 0.43)^(5 - 5)\)
\(P(X = 5) = 0.43^5 * 0.57^0\)
\(P(X = 5) = 0.43^5\)
Calculating this value:
P(X = 5) ≈ 0.0434
Therefore, the probability that 5 randomly selected American pet owners will have a photograph of their pet in their wallet is approximately 0.0434, rounded to 3 decimal places.
Learn more about probability here:
https://brainly.com/question/31740607
#SPJ11
A law firm is going to designate associates and partners to a big new case. The daily rate charged to the client for each associate is $500 and the daily rate for each partner is $1000. The law firm assigned a total of 14 lawyers to the case and was able to charge the $12000 per day for these lawyers' services. Graphically solve a system of equations in order to determine the number of associates assigned to the case, x, and the number partners assigned to the case, y.
Answers
Answer:
830
Step-by-step explanation:
Just divide the number by 7
Find the slope of the following graph.
yaxis
(2.2)
(1.2)
Answers
Answer:
Y = 2
Step-by-step explanation:
Use the formula below to find the slope. Plug 0 in for X to find the y intercept. In this case there is no slope. Make sure next time to use commas , instead of periods . when writing coordinates.

HELP ME HELP ME HELP ME
HELP ME , PLEASEEEEEE !!!!!!

Answers
Answer:
i dont know
good luck
Step-by-step explanation:
Answer:
7.5
Step-by-step explanation:
triangle ABC and XBY are similar so the sides are in proportion
BX /BY = BA /BC
4/6 = 5/BC; cross multiply
4*BC = 5*6 ; divide both sides by 4
BC= 5*6/ 4 = 30 /4 = 7.5
Mrs. Pruitt carves children's toys out of wood and sells them through an online store. Last week, she sold 6 cars, 3 fire trucks, 9 trains, 6 tractors, and 6 helicopters. The helicopters take the longest to carve. What percent of the toy sales were helicopters? %
Answers
Ans:- To determine the percentage of toy sales that were helicopters, we needed to determine the total number of toys sold and then calculate the proportion of that totally made up by helicopters.
step-1
The total number of toys sold isstep-26 + 3 + 9 + 6 + 6 = 30step-3The number of helicopters sold is:-6step-4To find the percentage, we need to divide the number of helicopters sold by the total number of toys sold and then multiply by 100:(6 / 30) x 100 = 20%step-5Therefore, 20% of toy sales were helicopters.
What is the radius of the circle? cm
What is the circumference of the circle?
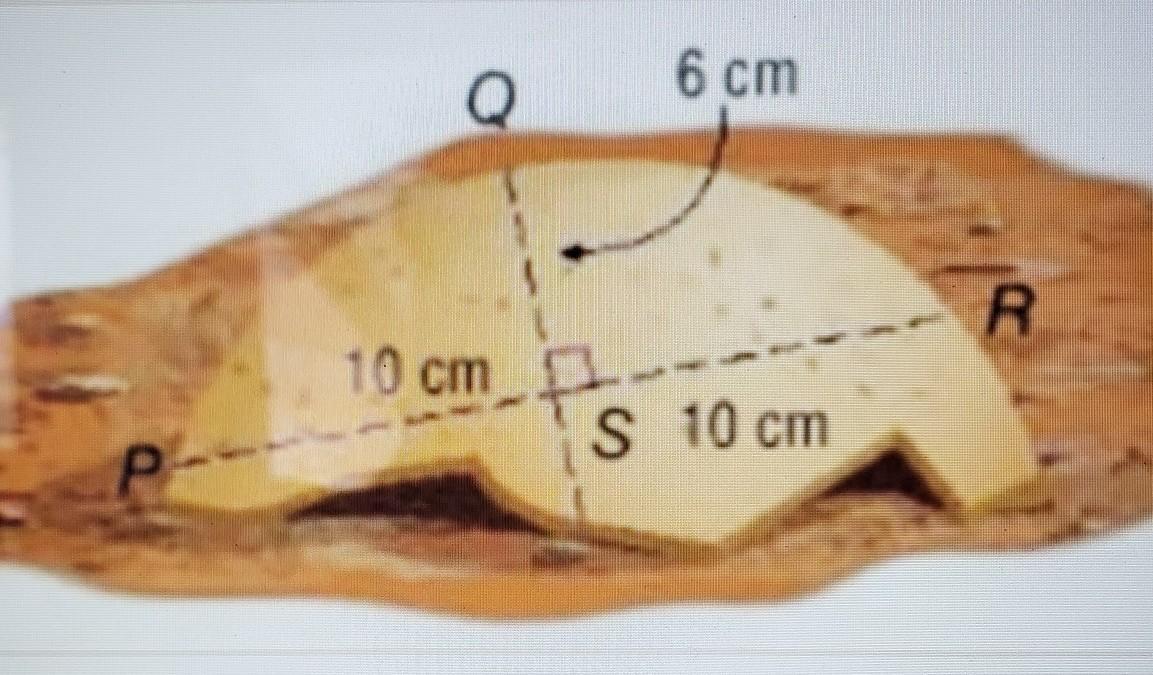
Answers
What is the measure of x?

Answers
Answer:
x = 78Step-by-step explanation:
\(m\angle BHD=180^o-x^o\)
\(m\angle DBH+m\angle BHD+m\angle HDB=180^o\\\\47^o+180^o-x^o+31^o=180^o\\\\78^o-x^o=0\\\\x^o=78^o\)
what is -3 to the -3 power
Answers
Answer:
-0.03
Step-by-step explanation:
\(3^{-3}=\frac{1}{3^3}\\=-\frac{1}{3^3}\\3^3=27\\=-\frac{1}{27}\\= -0.03\)
1. Define "Conjugate radical binomials."
Answers
Step-by-step explanation:
For a+b, it's a−b. A conjugate is a binomial where the second term is the opposite of the second term of another binomial. In other words, if I have the expression a+b, the conjugate of my expression is a−b. If I were to add the second terms of these two expressions, I would get 0.
Consider a continuous-time Markov chain with three states 1, 2, 3, 4, 5 and transition rates q12=1, q13 = 2, q21 = 0, q23 = 3, q31 = 0, q32 = 0. (1) Write the system of ODEs for the corresponding transition probabilities Pᵢⱼ (t) . (2) Suppose that the initial state is 1. What is the probability that after the first transition, the process X(t) enters state 2?
Answers
the probability of transitioning from state 1 to state 2 after the first transition is:
P(X(t) enters state 2 after the first transition | X(0) = 1) = 1 / 3
To write the system of ordinary differential equations (ODEs) for the transition probabilities Pᵢⱼ(t) of the given continuous-time Markov chain, we need to consider the rate at which the system transitions between different states.
Let Pᵢⱼ(t) represent the probability that the Markov chain is in state j at time t, given that it started in state i at time 0.
The ODEs for the transition probabilities can be written as follows:
dP₁₂(t)/dt = q₁₂ * P₁(t) - q₂₁ * P₂(t)
dP₁₃(t)/dt = q₁₃ * P₁(t) - q₃₁ * P₃(t)
dP₂₁(t)/dt = q₂₁ * P₂(t) - q₁₂ * P₁(t)
dP₂₃(t)/dt = q₂₃ * P₂(t) - q₃₂ * P₃(t)
dP₃₁(t)/dt = q₃₁ * P₃(t) - q₁₃ * P₁(t)
dP₃₂(t)/dt = q₃₂ * P₃(t) - q₂₃ * P₂(t)
where P₁(t), P₂(t), and P₃(t) represent the probabilities of being in states 1, 2, and 3 at time t, respectively.
Now, let's consider the second part of the question: Suppose that the initial state is 1. We want to find the probability that after the first transition, the process X(t) enters state 2.
To calculate this probability, we need to find the transition rate from state 1 to state 2 (q₁₂) and normalize it by the total rate of leaving state 1.
The total rate of leaving state 1 can be calculated as the sum of the rates to transition from state 1 to other states:
total_rate = q₁₂ + q₁₃
Therefore, the probability of transitioning from state 1 to state 2 after the first transition can be calculated as:
P(X(t) enters state 2 after the first transition | X(0) = 1) = q₁₂ / total_rate
In this case, the transition rate q₁₂ is 1, and the total rate q₁₂ + q₁₃ is 1 + 2 = 3.
Therefore, the probability of transitioning from state 1 to state 2 after the first transition is:
P(X(t) enters state 2 after the first transition | X(0) = 1) = 1 / 3
Learn more about probability here
https://brainly.com/question/32117953
#SPJ4
Find f(g(2)) if f(x) = 2x-1 g(x) = -3x Find f(g(2)) if f(x) = 2x-1 g(x) = -3x -6 -9 3 -13Let Q (in grams) represent the mass of a quantity of carbon-14, which has a half-life of 5730 years. The quantity present after t years is Q(t)=10\cdot\left(\frac12\right)^{\left(\frac t{5730}\right)}Q(t)=10⋅(
2
1
)
(
5730
t
)
.
Determine the quantity present after 2000 years.
Let Q (in grams) represent the mass of a quantity of carbon-14, which has a half-life of 5730 years. The quantity present after t years is Q(t)=10\cdot\left(\frac12\right)^{\left(\frac t{5730}\right)}Q(t)=10⋅(
2
1
)
(
5730
t
)
.
Determine the quantity present after 2000 years.
7.851 grams
1.117 grams
0.785 grams
1.745 grams
Answers
The quantity that is present after 2000 years will be A. 7.851 grams.
How to calculate the quantity?From the information given, initially at t = 0, the quantity is 10 grams.
After 2000 years, the appropriate quantity will be:
Q(2000) = 10 (1/2) × (2000/5730)
Q(2000) = 7.851 grams.
In conclusion, the correct option is A.
Learn more about quantity on:
brainly.com/question/13799721
#SPJ1
A shoe store recorded the number of customers who made a purchase out of a sample of 100 customers who entered the store each day. The boxplot shown summarizes the recorded data for one year. Based on the boxplot, which of the following statements is true?
A. The range of the number of customers making a purchase is greater than 32.
B. The interquartile range of the number of customers making a purchase is 25.
C. The number of days that had at least 26 customers making a purchase is greater than the number of days that had at most 11 customers making a purchase
D. The number of days that had from 11 to 26 customers making a purchase is equal to the number of days that had at most 14 customers making a purchase.
E.The difference between the median and the lower quartile for the customers making a purchase is less than 2.
Explain your thinking.

Answers
Less than 2 units separate the median from the lower quartile for customers making purchases.
What is meant by quartile deviation?The three values known as quartiles divide sorted data into four equal-sized portions, each with an equal number of observations. An example of a quantile is a quantile. First quartile: Also referred to as the lower quartile or Q1. The median or second quartile is also referred to as Q2. Third quartile: Also referred to as the higher quartile or Q3.
Half of the difference between the upper and lower quartiles can be used to define the quartile deviation analytically. Here, the upper quartile (Q3) and lower quartile (Q1) can be used to depict quartile deviation as the letters QD. The term "quartile deviation" is sometimes used to refer to the semi-interquartile range.
The coefficient of quartile deviation serves as a gauge for a collection of data's variability or spread. It is determined by taking the square root of the difference between the upper and lower quartiles, squaring the result, and dividing it by two. Comparing data sets is simple because it is expressed as a percentage.
Therefore, the correct answer is option E. The difference between the median and the lower quartile for the customers making a purchase is less than 2.
To learn more about quartile deviation refer to:
https://brainly.com/question/3806824
#SPJ1
Find the distance between the points.
(2,7),(2,9)
The distance is
Answers
Answer:
distance is 2 units
Step-by-step explanation:
9-7=2
Use the function f(x) to answer the questions:
f(x) = 2x2 − 3x − 5
Part A: What are the x-intercepts of the graph of f(x)? Show your work. (2 points)
Part B: Is the vertex of the graph of f(x) going to be a maximum or a minimum? What are the coordinates of the vertex? Justify your answers and show your work. (3 points)
Part C: What are the steps you would use to graph f(x)? Justify that you can use the answers obtained in Part A and Part B to draw the graph. (5 points)
Answers
a) The x-intercepts of the graph of f(x) are x = 2.5 and x = -1.
b) The coordinates of the vertex are (0.75, -5.125).
c) By using the x-intercepts and vertex obtained in Parts A and B, we can accurately depict the shape and positioning of the parabolic graph of f(x).
Part A: To find the x-intercepts of the graph of f(x), we set f(x) equal to zero and solve for x.
Setting f(x) = 0:
\(2x^2 - 3x - 5 = 0\)
To solve this quadratic equation, we can either factor it or use the quadratic formula. In this case, factoring is not straightforward, so let's use the quadratic formula:
x = (-b ± √(b^2 - 4ac)) / (2a)
For our equation, a = 2, b = -3, and c = -5. Substituting these values into the quadratic formula:
x = (-(-3) ± √((-3)^2 - 4(2)(-5))) / (2(2))
x = (3 ± √(9 + 40)) / 4
x = (3 ± √49) / 4
x = (3 ± 7) / 4
This gives us two possible solutions:
x1 = (3 + 7) / 4 = 10/4 = 2.5
x2 = (3 - 7) / 4 = -4/4 = -1
Therefore, the x-intercepts of the graph of f(x) are x = 2.5 and x = -1.
Part B: To determine whether the vertex of the graph of f(x) is a maximum or minimum, we need to consider the coefficient of the x^2 term in the function f(x). In this case, the coefficient is positive (2), which means the parabola opens upward and the vertex represents a minimum point.
To find the coordinates of the vertex, we can use the formula x = -b / (2a). In our equation, a = 2 and b = -3:
x = -(-3) / (2(2))
x = 3 / 4
x = 0.75
To find the corresponding y-coordinate, we substitute x = 0.75 into the function f(x):
f(0.75) = 2(0.75)^2 - 3(0.75) - 5
f(0.75) = 2(0.5625) - 2.25 - 5
f(0.75) = 1.125 - 2.25 - 5
f(0.75) = -5.125
Therefore, the coordinates of the vertex are (0.75, -5.125).
Part C: To graph the function f(x), we can follow these steps:
Plot the x-intercepts obtained in Part A: (2.5, 0) and (-1, 0).
Plot the vertex obtained in Part B: (0.75, -5.125).
Determine if the parabola opens upward (as determined in Part B) and draw a smooth curve passing through the points.
Extend the curve to the left and right of the vertex, ensuring symmetry.
Label the axes and any other relevant points or features.
By using the x-intercepts and vertex obtained in Parts A and B, we can accurately depict the shape and positioning of the parabolic graph of f(x).
The x-intercepts help determine where the graph intersects the x-axis, and the vertex helps establish the lowest point (minimum) of the parabola. The resulting graph should show a U-shaped curve opening upward with the vertex at (0.75, -5.125) and the x-intercepts at (2.5, 0) and (-1, 0).
For more such questions on intercepts visit:
https://brainly.com/question/24212383
#SPJ8
help someone need help on this question

Answers
The area of the figure is 141.5 units²
What is area of figures?The space enclosed by the boundary of a plane figure is called its area. The area is measured in units².
The figure can be sub divided into 3 parts,
The first part is a rectangle,
Area of rectangle = l× w
= 6× 8
= 48units²
The second part is also a rectangle
The area of a rectangle = l×w
= 5 × 11
= 55 unit²
The third part is a triangle
area of a triangle = 1/2 bh
= 1/2 × 11 × 7
= 77/2 = 38.5 units²
therefore the area of the figure = 38.5 + 55+48
= 141.5 units²
learn more about area of figures from
https://brainly.com/question/11423300
#SPJ1
A student is standing, with her arms outstretched, on a platform that is rotating at 1.6 rev/s. She pulls her arms in and the platform now rotates at 2.2 rev/s. Her original moment of inertia (I0) is 25 kg m2.
What is her final moment of inertia (If)?
Answers
The student's final moment of inertia is 18.18 kgm².
What is moment of inertia?The moment of inertia of an objecr is the property of an object which shows its ability to rotate.
How to find the final moment of inertia?Since a student is standing with her arms outstretched, on a platform that is rotating at 1.6 rev/s. She pulls her arms in and the platform now rotates at 2.2 rev/s. Her original moment of inertia (I0) is 25 kgm². To find the r final moment of inertia, we use the law of conservation of angular momentum.
What is the law of conservation of angular momentum?The law of conservation of angular momentum states that for any rotation, angular momnetum is constant.
So, Iω = constant where
I = moment of inertia and ω = angular speed.So, Iω = I'ω' where
I = initial moment of inertia of student = 25kgm²ω = initial angular speed of student = 1.6 rev/s I' = final moment of inertia of student ω' = final angular speed of student = 2.2 rev/sMaking I' subject of the formula, we have that
I' = Iω/ω'
So, substituting the values of the variables into the equation, we have that
I' = Iω/ω'
I' = 25 kgm² × 1.6 rev/s ÷ 2.2 rev/s
= 40 kgm²rev/s ÷ 2.2 rev/s
= 18.18 kgm²
So, the final moment of inertia is 18.18 kgm².
Learn more about moment of inertia here:
https://brainly.com/question/29471030
#SPJ1
Which of the equations below have one solution? Select all that apply. 8x–3x+5=5x–2 9=3(5x–2) 6x–(3x+8)=16 9x+4–x=4(2x+1)
Answers
Answer:
The equations that have one solution are 9=3(5x–2) and 6x–(3x+8)=16
Step-by-step explanation:
To determine which equations have one solution, we will determine the solution(s) to all the equations (that is, find the value of the unknown, x).
1. 8x–3x+5=5x–2
This becomes
5x+5=5x-2
Subtract 5x from both sides
5x-5x+5 = 5x-5x-2
0+5 = 0-2
This equation has no solution
2. 9=3(5x–2)
First, open the bracket by distributing 3
∴ 9 = 15x - 6
Then, add 6 to both sides
9+6 = 15x -6 +6
15 = 15x
Divide both sides by 15
15/15 = 15x/15
1 = x
∴ x = 1
This has one solution.
3. 6x–(3x+8)=16
Open the bracket by distributing –1
6x -3x -8 = 16
3x - 8 = 16
Add 8 to both sides
3x -8 +8 = 16 + 8
3x = 24
Divide both sides by 3
3x/3 = 24/3
x = 8
This has one solution.
4. 9x+4–x=4(2x+1)
This becomes
9x -x +4 = 4(2x+1)
Then, 8x +4 = 4(2x+1)
Open the bracket by distributing 4
8x +4 = 8x +4
This is true for any value of x.
Hence, the equations that have one solution are 9=3(5x–2) and 6x–(3x+8)=16.