Answers
Related Questions
My teacher gave me an extra credit assignment with 25 minutes left of class. It is extra credit, not a timed assessment.
need done as soon as possible

Answers
Answer: it will be square or rhombus
Step-by-step explanation:
392 x 22 but in a reciprocal answer I only have 10 minutes!!
Answers
your answer is 0.00011596

What is the slope of the line whose equation is y-6=2(x+3)?
Answers
Answer:
2
Step-by-step explanation:
y=mx+n m is slope
y-6=2(x+3) so y=2x+12 m=2 is slope.
Help Please Math is so stressful

Answers
Answer:
A=-6
Step-by-step explanation:
Answer:
B, D, and E
Step-by-step explanation:
If f(x) -
X-3
and g(x) = 5x - 4, what is the domain of (f•g)(x)?
Answers

Seth is using the figure shown below to prove Pythagorean Theorem using triangle similarity:
In the given triangle ABC, angle A is 90° and segment AD is perpendicular to segment BC.
The figure shows triangle ABC with right angle at A and segment AD. Point D is on side BC.
Which of these could be a step to prove that BC2 = AB2 + AC2?
possible answers -
By the cross product property, AB2 = BC multiplied by BD.
By the cross product property, AC2 = BC multiplied by BD.
By the cross product property, AC2 = BC multiplied by AD.
By the cross product property, AB2 = BC multiplied by AD.

Answers
The correct step to prove that \(BC^2 = AB^2 + AC^2\) is:
By the cross product property, \(AC^2 = BC \cdot AD\).
To prove that \(BC^2 = AB^2 + AC^2\), we can use the triangle similarity and the Pythagorean theorem. Here's a step-by-step explanation:
Given triangle ABC with right angle at A and segment AD perpendicular to segment BC.
By triangle similarity, triangle ABD is similar to triangle ABC. This is because angle A is common, and angle BDA is a right angle (as AD is perpendicular to BC).
Using the proportionality of similar triangles, we can write the following ratio:
\($\frac{AB}{BC} = \frac{AD}{AB}$\)
Cross-multiplying, we get:
\($AB^2 = BC \cdot AD$\)
Similarly, using triangle similarity, triangle ACD is also similar to triangle ABC. This gives us:
\($\frac{AC}{BC} = \frac{AD}{AC}$\)
Cross-multiplying, we have:
\($AC^2 = BC \cdot AD$\)
Now, we can substitute the derived expressions into the original equation:
\($BC^2 = AB^2 + AC^2$\\$BC^2 = (BC \cdot AD) + (BC \cdot AD)$\\$BC^2 = 2 \cdot BC \cdot AD$\)
It was made possible by cross-product property.
Therefore, the correct step to prove that \(BC^2 = AB^2 + AC^2\) is:
By the cross product property, \(AC^2 = BC \cdot AD\).
For more questions on cross-product property:
https://brainly.com/question/14542172
#SPJ8
22\5= how many /10?
44
22
11
Or
10
Answers
Answer:
the correct answer is 44
Step-by-step explanation:
22/5 = 4.4
44/ 10 = 4.4
please help me with this its due in 15 minutes plus ill need help with more

Answers
Answer:
171 Square Feet
Step-by-step explanation:
We first cut the figure up into smaller parts...
we then use the formula (L x W = A) to find the area
L = Lenth
W = Width
the first rectangle (1)...
15 x 5 = 75
the second figure (2)...
8 x 9 = 72
the third figure (3)...
6 x 4 = 24
now we have to add up all the values to find the area of the entire figure...
75 + 72 + 24 = 171
Hope this helps! Please let me know if you need more help or think my answer is incorrect. Brainliest would be MUCH appreciated. Also remember to rate answers to help other students, While leaving thanks to answers that help you. Have a great day!

All of the license plates in a particular state feature three letters followed by three digits (e.g. ABC 123). How many different license plate numbers are available to the state's Department of Motor Vehicles?
Answers
Step-by-step explanation:
for each letter position there are 26 choices.
and each of these 26 choices can be combined with the next 26 choices.
so, they alone are 26×26×26 = 26³ = 17,576
then we have the three number positions.
each has 10 options.
so, they are 10×10×10 = 10³ = 1000
and both combined are
26³×10³ = 17,576,000 different number plates
The number of different license plate numbers are available to the state's Department of Motor Vehicles is 17,575,000.
What is fundamental counting principle?The fundamental counting principle or basic principle of counting is a method or a rule used to calculate the total number of outcomes when two or more events are occurring together.
This principle states that the total number of outcomes of two or more independent events is the product of the number of outcomes of each individual event.
For each letter position there are 26 choices, and each of these 26 choices can be combined with the next 26 choices.
so, they alone are 26×26×26 = 26³ = 17,576
then we have the three number positions, each has 10 options.
so, they are 10×10×10 = 10³ = 1000
and both combined are;
26³×10³ = 17,576,000 different number plates.
Hence the number of different license plate numbers are available to the state's Department of Motor Vehicles is 17,575,000.
Learn more about fundamental counting principle, click;
https://brainly.com/question/28384306
#SPJ2
If the sum of three consecutive numbers is 738, what is the middle one?
Answers
Answer:
The logical answer is 246
Step-by-step explanation: So, (X+1)+ (X+2) + (X+3)=738 then 3x+3=738 so x=245. 245 is the first number so then the answer is 245+246+247=738. And that leads to the conclusion that the middle number is 246.
Given the ABC, where A(4,3), B(2,-1), and C(-2,1). Use the slope and distance formula to classify the triangle.
Answers
It might be 2 not 100 percent sure
Answer:
isosceles (based on sides) and right triangle (based on angles)
Step-by-step explanation:
This is an isosceles triangle because two of the sides are the same distance (it is in cm.). This is also a right triangle because at point B the two lines are perpendicular (using their slopes).


Solve for n. You must write your answer in fully simplified form.
- 4n = -5
Answers
1.25 or 5/4
Step-by-step explanation:
n=-5/-4
2. Simplify
n=5/4, or as a mixed number n=1 1/4, or as a decimal 1.25
Can someone help me please?
ASAP

Answers
Answer:
y = 12 x = 12\(\sqrt{3}\)
Step-by-step explanation:
This is a 60, 90, 30. It's a special triangle.
2z = 24
z = 12
If x = z\(\sqrt{3}\)
then x = 12\(\sqrt{3}\)
y = z itself
So y = 12

A construction crew is pouring concrete to make a floor in a building. The weight of the concrete is proportional to the volume of concrete that has been poured. After pouring 5 cubic feet they know the weight of the concrete is 740 pounds.
(b). The crew wants to create an equation of the form w=k*v to calculate the weight of the concrete based on its volume in cubic feet. What is the value of k in this equation? explain
Answers
The equation that can be used to calculate the concrete weight, w = k·v, and the 740 pounds weight of 5 cubic feet concrete, gives the value of k (which is the density of the concrete) as 148 lb/ft³
What is the density of a substance?The density of a material is the ratio of the mass of the material to its volume.
(b) The weight, w of the concrete is directly proportional to the volume, v of the concrete
The weight of 5 cubic feet = 740 pounds
The equation that can be used to calculate the weight of a given volume of concrete is; w ∝ v
w = k·vWhere;
k = The constant of proportionality
Which gives;
\(k = \dfrac{w}{v}\)
In a proportional relationship between two variables, one variable is a constant multiple of the other such that the ratio of the two variables is a constant, k, which can be found using the value for the data point in the question;
When the weight is 740 pounds, the volume is 5 cubic feet, which gives;
\(k = \dfrac{740\, lb }{5\, ft^3} = 148\, lb/ft^3\)
The value of k in the equation is 148 lb/ft.³Learn more about the constant of proportionality here:
https://brainly.com/question/22167107
#SPJ1
find the sum
-84 + (-11)
Answers
Answer:
-84+(-11)= -95
-84 + (-11) = -84 - 11 = -95
By the commutative property, adding a negative number is the same as subtracting that number as a positive; therefore, something + (-11) = something - 11. After changing the equation from -84 + (-11) to -84 - 11, we use regular addition properties, adding the tens place and ones place to get -95.
In the diagram below, if the measure of < C = 45 °, and side AC = 10, then side BC = _____.

Answers
Solution:
Given:
Using the trigonometric ratio of cosine,
\(\begin{gathered} cos\theta=\frac{adjacent}{hypotenuse} \\ cos45=\frac{BC}{10} \\ BC=10\times cos\text{ 45} \\ BC=10\times\frac{\sqrt{2}}{2} \\ BC=5\sqrt{2} \end{gathered}\)Therefore, OPTION A is correct.

What is the value of x in the equation −6 + x = −2? Answer A. 8 B. 3 C. -4 D. -8
someone help me
Answers
Answer:
x = 4
Step-by-step explanation:
You can solve for "x" by rearranging the equation and getting the "x" by itself on one side. Remember, whatever you do to one side of the equation, you must do to the other side.
-6 + x = -2 <----- Original equation
+6 +6 <----- Add 6 to both sides to isolate "x"
0 + x = 4 <----- After the addition
x = 4 <----- Rewrite
Answer:
None of the above (x = 4) \( \sf {} \)
Step-by-step explanation:
Now we have to,
→ find the required value of x.
The equation is,
→ -6 + x = -2
Then the value of x will be,
→ -6 + x = -2
→ x = -2 + 6
→ [ x = 4 ]
Hence, the value of x is 4.
What is −5/6÷9/10? DO YOU LIKE CHEESE?
−27/25
−4/3
−25/27
−3/4
Answers
Answer:
− 25 /27
Step-by-step explanation:
Answer:
-25/27
Step-by-step explanation:
get fraction calculator plus very helpful on Android and Apple
Boris started on the treadmill after setting timer for 99 minutes. The display says he have finished 43% of his run. How many minutes have gone by. Round to the nearest tenth
Answers
99 minutes * 0.43 = 42.57 minutes
Rounding to the nearest tenth, we can say that approximately 42.6 minutes have gone by.
Find the inverse of the function below and sketch by hand a graph of both the function and is inverse on the same coordinate plane. Share all steps as described in the lesson to earn full credit. Images of your hand written work can be uploaded. f(x)=(x+3)^2 with the domain x \geq-3
Answers
In order to find the inverse of f(x), let's switch x by f^-1(x) and f(x) by x in the function, then we solve the resulting equation for f^-1(x).
So we have:
\(\begin{gathered} f(x)=(x+3)^2 \\ x=(f^{-1}(x)+3)^2 \\ \sqrt[]{x}=f^{-1}(x)+3 \\ f^{-1}(x)=-3+\sqrt[]{x} \end{gathered}\)(The domain of f(x) will be the range of f^-1(x), so the range of f^-1(x) is y >= -3)
In order to graph the function and its inverse, we can use some points that are solutions to each one.
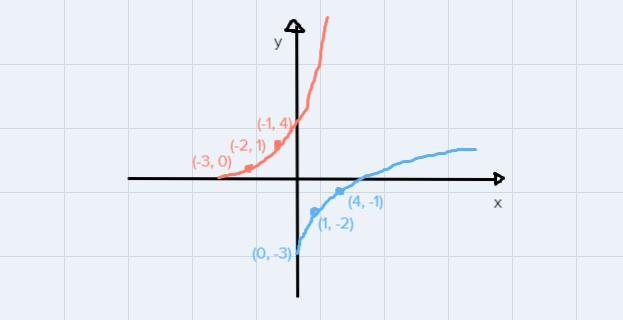
For f(x), let's use (-3, 0), (-2, 1) and (-1, 4).
For f^-1(x), let's use (0, -3), (1, -2) and (4, -1).
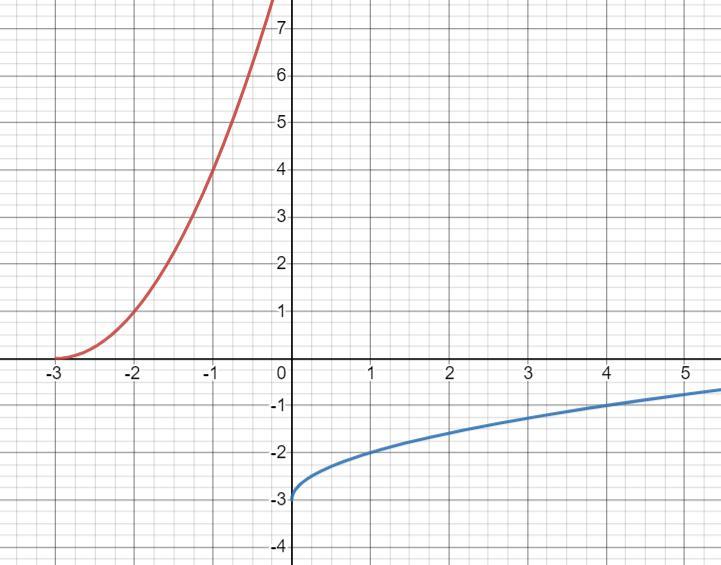
Graphing f(x) in red and f^-1(x) in blue, we have:
Graphing it manually, we have:
A cereal company wants to create a box that a volume that is double the size of its
original box. Which of the following could be used to double the volume?
Answers
Rewrite as a simplified fraction.
0.67 = ?
7 is repeating forever

Answers
Answer:
67/100
Step-by-step explanation:
its the simpelist form
It is 6 kilometers from Linda's house to the nearest mailbox. How far is it in meters?
Answers
Answer:
6000 meters
Step-by-step explanation:
Each kilometer is 1000 meters so 1000 x 6 is 6000
help me answer this please

Answers
Answer:
3,952 ft
Step-by-step explanation:
Use the sine function since you need to find the hypotenuse but know the opposite side of the angle, since sine is equal to opposite/hypotenuse.
sin8°=\(\frac{550}{c}\)
csin8°=550
c=550/sin8°
c= 3,952
Which binomial below is a factor of the polynomial 3a^2+6a-2a-4 A. (a – 2) B. (a + 4) C. (3a – 2) D. (3a + 2)
Answers
The solution is Option C.
The value of the quadratic equation is A = 3a² + 4a - 4 , where the factor of a is given by a = 2/3
What is Quadratic Equation?A quadratic equation is a second-order polynomial equation in a single variable x , ax² + bx + c=0. with a ≠ 0. Because it is a second-order polynomial equation, the fundamental theorem of algebra guarantees that it has at least one solution. The solution may be real or complex.
The roots of the quadratic equations are
x = [ -b ± √ ( b² - 4ac ) ] / ( 2a )
where ( b² - 4ac ) is the discriminant
when ( b² - 4ac ) is positive, we get two real solutions
when discriminant is zero we get just one real solution (both answers are the same)
when discriminant is negative we get a pair of complex solutions
Given data ,
Let the quadratic equation be represented as A
Now , the value of A is
A = 3a² + 6a - 2a - 4 be equation (1)
On simplifying the equation , we get
A = 3a² + 4a - 4
Now , when the factor of the equation is ( 3a - 2 ) = 0
Adding 2 on both sides of the equation , we get
3a = 2
Divide by 3 on both sides , we get
a = 2/3
Substitute the value of a in the equation , we get
A = 3 ( 2/3 )² + 4 ( 2/3 ) - 4
On simplifying the equation , we get
A = 3 ( 4/9 ) + 8/3 - 4
A = ( 4/3 + 8/3 ) - 4
A = ( 12/3 ) - 4
A = 4 - 4
A = 0
Hence , the binomial ( 3a - 2 ) is a factor of the equation
To learn more about quadratic equations click :
https://brainly.com/question/25652857
#SPJ1
triangle MNO is an isosceles triangle in which only one angle measures 88.6. what is the angle measure of one of the two congruent angles?
Answers
Answer:
45.7°
Step-by-step explanation:
area of a triangle= 180°so,180- 88•6=91•4since the congruent angles are equal,you will divide 91•4 by 291•4÷2=45•7ans=45•7°Algebra PLS HELP!!!!!!!!!!!!!
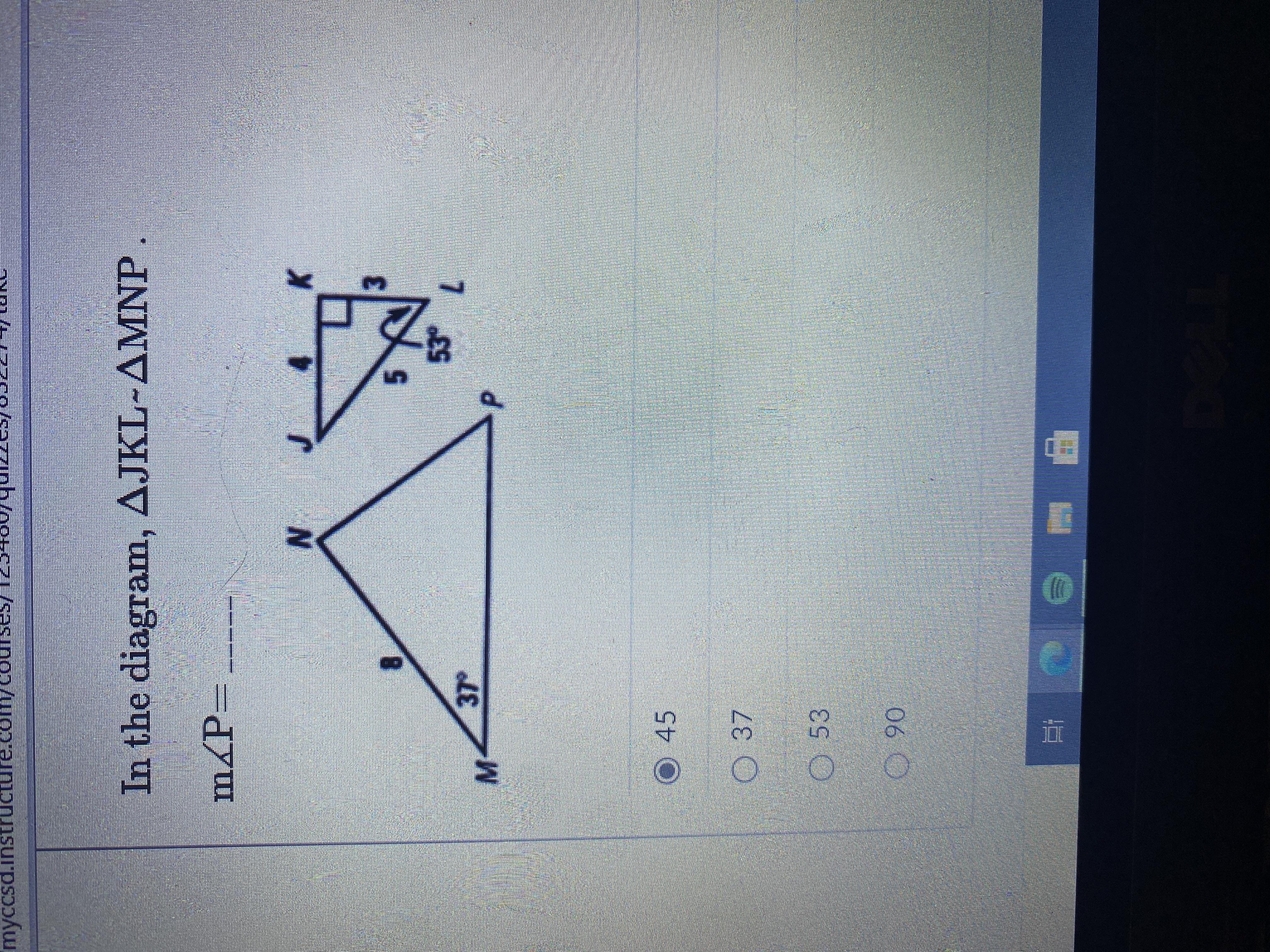
Answers
Answer:
C - 53 Degrees
Step-by-step explanation:
HELP i need this awnser now
simplify 2/3 + 1/12 + 1/4
Answers
Answer:
this is your answer
Step-by-step explanation:
please mark as brainlist
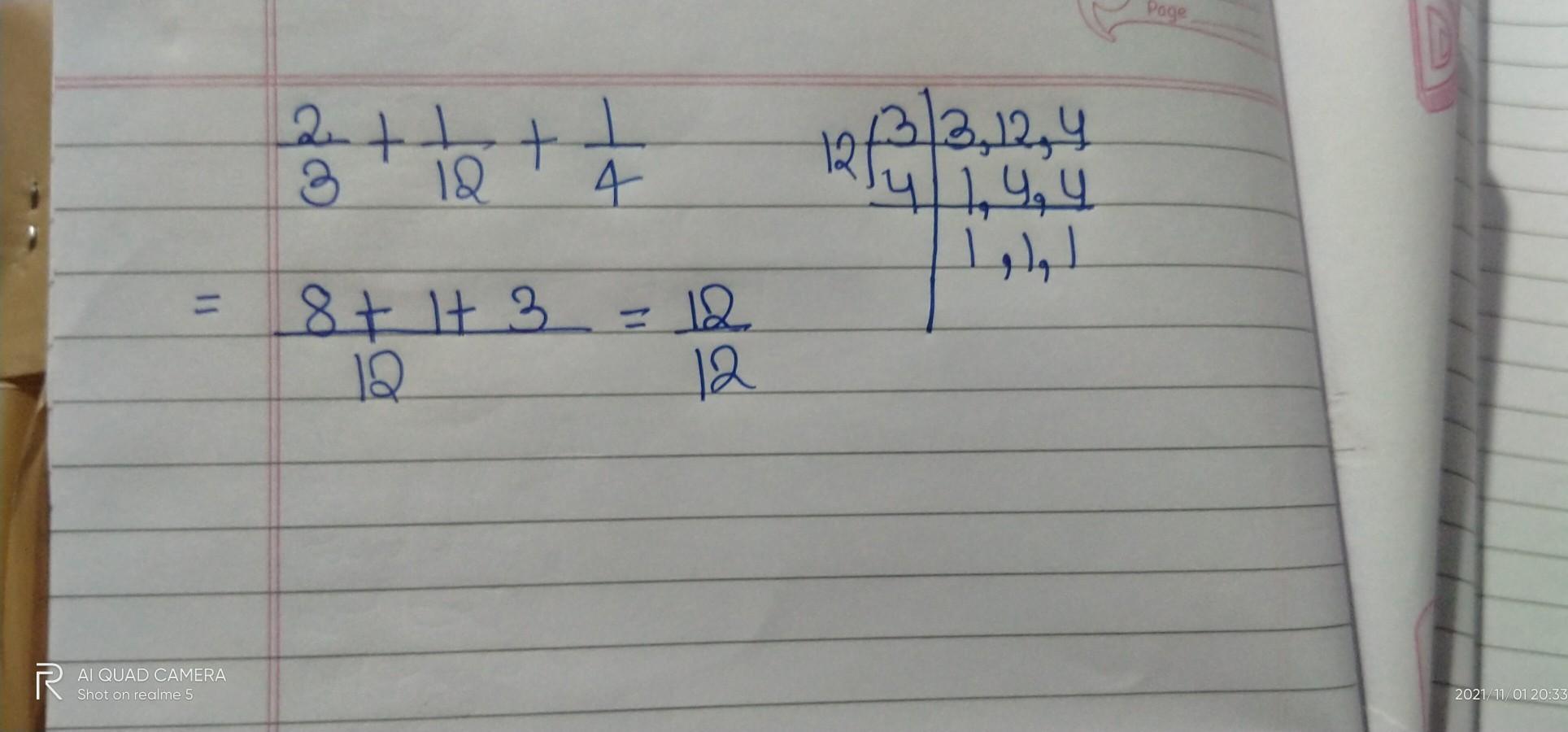
PLEASE I NEED HELP the question is,
In the diagram of triangle LAC and triangle DNC below, LA = DN, CA = CN, and DAC is perpendicular to LCN.
a) Prove that triangle LAC = triangle DNC.
b) Describe a sequence of rigid motions that will map triangle LAC onto triangle DNC.
Answers
Answer:
1244 DCD
Step-by-step explanation:
find the area of the circle which is circumscribed about the right triangle with legs 6 and 8
Answers
The area of the circle circumscribed about the right triangle with legs 6 and 8 is approximately 78.54 square units.
To find the area of the circle circumscribed about a right triangle, we can use the fact that the diameter of the circle is equal to the hypotenuse of the right triangle. In this case, the legs of the right triangle are given as 6 and 8.
Using the Pythagorean theorem, we can find the length of the hypotenuse:
\(c^2 = a^2 + b^2\)
where c is the length of the hypotenuse, and a and b are the lengths of the legs.
Substituting the values:
\(c^2 = 6^2 + 8^2\)
\(c^2 = 36 + 64\\ c^2 = 100\)
Taking the square root of both sides:
\(c = \sqrt{100} \\ c = 10\)
Therefore, the length of the hypotenuse is 10 units.
Since the diameter of the circumscribed circle is equal to the hypotenuse, the radius of the circle is half the length of the hypotenuse, which is 10/2 = 5 units.
Now we can calculate the area of the circle using the formula:
Area = π \(r^2\)
where r is the radius of the circle.
Area = π \(5^2\)
Area = π × 25
Area = 78.54 square units
Hence, the area of the circle circumscribed about the right triangle with legs 6 and 8 is approximately 78.54 square units.
For more questions on area
https://brainly.com/question/22972014
#SPJ8
