Write the equation of line of the line that passes through the point (5, 6) and a slope of 2
Answers
Related Questions
let a and b be integers. prove that if ab = 4, then (a – b)3 – 9(a – b) = 0.
Answers
Let \(\(a\)\) and \(\(b\)\) be integers such that \(\(ab = 4\)\). We want to prove that \(\((a - b)^3 - 9(a - b) = 0\).\)
Starting with the left side of the equation, we have:
\(\((a - b)^3 - 9(a - b)\)\)
Using the identity \(\((x - y)^3 = x^3 - 3x^2y + 3xy^2 - y^3\)\), we can expand the cube of the binomial \((a - b)\):
\(\(a^3 - 3a^2b + 3ab^2 - b^3 - 9(a - b)\)\)
Rearranging the terms, we have:
\(\(a^3 - b^3 - 3a^2b + 3ab^2 - 9a + 9b\)\)
Since \(\(ab = 4\)\), we can substitute \(\(4\)\) for \(\(ab\)\) in the equation:
\(\(a^3 - b^3 - 3a^2(4) + 3a(4^2) - 9a + 9b\)\)
Simplifying further, we get:
\(\(a^3 - b^3 - 12a^2 + 48a - 9a + 9b\)\)
Now, notice that \(\(a^3 - b^3\)\) can be factored as \(\((a - b)(a^2 + ab + b^2)\):\)
\(\((a - b)(a^2 + ab + b^2) - 12a^2 + 48a - 9a + 9b\)\)
Since \(\(ab = 4\)\), we can substitute \(\(4\)\) for \(\(ab\)\) in the equation:
\(\((a - b)(a^2 + 4 + b^2) - 12a^2 + 48a - 9a + 9b\)\)
Simplifying further, we get:
\(\((a - b)(a^2 + 4 + b^2) - 12a^2 + 39a + 9b\)\)
Now, we can observe that \(\(a^2 + 4 + b^2\)\) is always greater than or equal to \(\(0\)\) since it involves the sum of squares, which is non-negative.
Therefore, \(\((a - b)(a^2 + 4 + b^2) - 12a^2 + 39a + 9b\)\) will be equal to \(\(0\)\) if and only if \(\(a - b = 0\)\) since the expression \(\((a - b)(a^2 + 4 + b^2)\)\) will be equal to \(\(0\)\) only when \(\(a - b = 0\).\)
Hence, we have proved that if \(\(ab = 4\)\), then \(\((a - b)^3 - 9(a - b) = 0\).\)
To know more about satisfies visit-
brainly.com/question/16993710
#SPJ11
give me 5 things u want for Christmas and 3 words to describe you :))
Answers
Answer: Baggy clothes, a new phone, art supplies, jewelry, posters(marvel, Billie Eilish, and just some random posters that I love) and room decorations.
Step-by-step explanation:
:D
83. (a) by comparing areas, show that
\( \frac{1}{3}\ \textless \ \ln 1.5\ \textless \ \frac{5}{12} \)
Answers
To compare the values \(\(\frac{1}{3}\), \(\ln 1.5\)\), and \(\(\frac{5}{12}\)\), we can use the concept of areas. However, the provided sequence, 64, 112, 196, 343, does not give enough information to determine the common ratio.
(a) To compare the values \(\(\frac{1}{3}\), \(\ln 1.5\), and \(\frac{5}{12}\)\), we can utilize the concept of areas. We start by considering the area under the curve of the function \(\(y = \frac{1}{x}\) between \(x = 1\) and \(x = 1.5\)\). The area of this region represents \(\ln 1.5\). Similarly, we divide the area under the curve of \(\(y = \frac{1}{x}\) between \(x = 1\) and \(x = 2\)\) into three equal regions. The middle region represents \(\frac{1}{3}\), and the rightmost region represents \(\(\frac{5}{12}\)\). By comparing the areas visually or using calculus, we can confirm that \(\(\frac{1}{3} \ < \ \ln 1.5 \ < \ \frac{5}{12}\)\).
However, the second part of the question, regarding finding the common ratio in the sequence 64, 112, 196, 343, cannot be answered with the given information. A geometric sequence follows the pattern where each term is obtained by multiplying the previous term by a constant value called the common ratio. Without knowing the pattern or additional terms of the sequence, we cannot determine the common ratio. Therefore, we cannot provide a value rounded to the nearest hundredth for the common ratio in this sequence.
Learn more about common ratio here:
https://brainly.com/question/17630110
#SPJ11
Please help on this I’m lost

Answers
Answer:
B) Reflect triangle ABC across line BC
and the 2nd one is also B
Step-by-step explanation:
Hope this helps! Pls give brainliest!
What is the value of 1 − 2 × 3 + 4 ÷ 5 ?
Answers
Answer: -4.2
Step-by-step explanation:
=1-6+0.8
=-4.2
11 / 5
= 2.2
PLEASE HELP I DONT UNDERSTAND
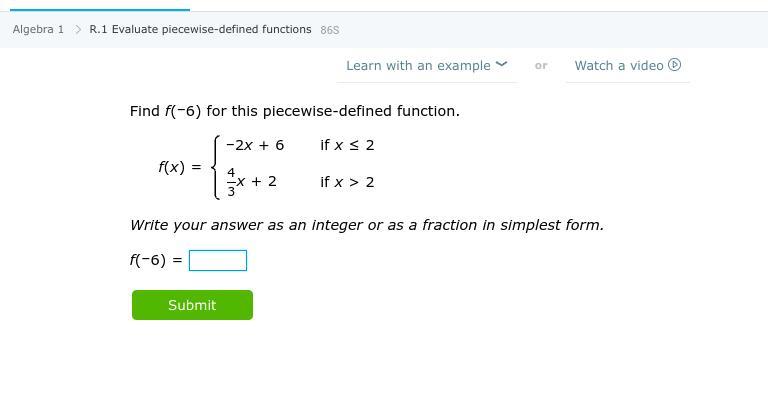
Answers
Answer:
18
Step-by-step explanation:
X= -6 which is x≤2
So,
f(-6) = -2(-6)+6
= 18
Hurry please !!! I need this

Answers
Answer: -2 1/16
if you add it all together it should be 2 1/16
hoped this helped let me know if it did
Write 3 3/4 as a decimal
Answers
Answer: 3.75
Step-by-step explanation:
3 is a whole number and 3/4 is 75% of 100 so this is why the answer is 3.75.
Hope this helps :)
Answer:3.75
Step-by-step explanation:
Midpoint Between Two Given Points Find the midpoint of the line segment with the endpoints (5, 6) and (-5, -2). Midpoint = (
Answers
The midpoint of the line segment with the endpoints (5, 6) and (-5, -2) is (0, 2).Hence, the answer is: Midpoint = (0, 2).
The midpoint of a line segment with endpoints (x1, y1) and (x2, y2) is calculated using the formula:M = [(x1 + x2) / 2, (y1 + y2) / 2]where M is the midpoint.In the given problem, the endpoints are (5, 6) and (-5, -2).
So, we can find the midpoint by applying the formula mentioned above.Midpoint = [(5 + (-5)) / 2, (6 + (-2)) / 2]= [0/2, 4/2]= [0, 2]
for more search question segment
https://brainly.com/question/28322552
#SPJ8
Write a polynomial function of the least degree that has roots of 3 and (4 + i).
Answers
Answer:
your answer is 4+3
Step-by-step explanation:
need help asap - its geometry. thanks!

Answers
Answer:
The answer to the question is (-5, -9)
Perform the following area application
If 600 bricks measuring 12" by 18" are required to build a wall 10 ft. high (one brick thick), how long is the wall?
_________ft.
Answers
The first step is to calculate the total area of 600 bricks.
Area of one brick = 12 inches x 18 inches = 216 square inches
Area of 600 bricks = 600 x 216 = 129,600 square inches
Next, we need to convert the height of the wall from feet to inches since the area of the bricks is in square inches.
10 feet = 120 inches
Now, we can divide the total area of the bricks by the height of the wall to find the length of the wall.
Length of the wall = Area of 600 bricks / Height of the wall
Length of the wall = 129,600 square inches / 120 inches
Length of the wall = 1080 inches
Finally, we can convert the length of the wall back to feet by dividing by 12 since there are 12 inches in a foot.
Length of the wall = 1080 inches / 12 inches/foot
Length of the wall = 90 feet
Therefore, the length of the wall is 90 feet.
To solve this problem, we need to use the formula for calculating area which is length x width. We also need to convert units from feet to inches and vice versa as necessary to ensure we are working with the same units throughout the problem.
The length of the wall is 90 feet.
To know more about area visit:
https://brainly.com/question/30307509
#SPJ11
the file p02 45.xlsx contains the salaries of 30 business school professors at a (fictional) large state university. if you increased every professor's salary by $4,000, what would happen to the mean and median salary?
Answers
We are increasing every professor's salary by 4000, let this new salary be Yi for every professor then mean of new salary Y will be
Y = 1/n∑Yi
Y = 1/n∑(Xi + 4000)
Y = 1/n(∑Xi + ∑4000/n)
Y = X + 4000
Median Xm is the middle most value of the Professor's old salary, since new salary is
Yi = Xi + 4000
then new median salary Ym will be
Ym = Xm + 4000
To learn more about Salary click here:
http://brainly.com/question/14371457
Answer:
Step-by-step explanation:The mean and Median salary would increase by $4,000.
Let sum of the salaries be n1+n2+n3+.......... +n30
Mean = sum of observation / no. of observation
Thus,
Initial mean, M1 = n1+n2+n3+.......... +n30 / 30
When $4,000 is added to every salary 4000 is added 30 times to the sum.
Thus,
New mean, M2 = n1+n2+n3+.......... +n30 +( 4000 * 30)
30
= M1 + ( 4000 * 30)
30
Thus, M2 = M1+ 4000
Therefore, The mean salary increase by $4,000.
We know Median of even number of observation = [(n/2)th term + ((n/2) + 1)th term]/2
Here n/2th term is n15 and (n/2 +1)th term is n16
Thus,
Initial Median, Median 1 = n15 + n16
2
When $4,000 is increased in each salary
New Median, Median 2 = n15 + 4000 + n16 + 4000
2
= Median 1 + 2 * 4000
2
Thus, Median 2= Median 1 + 4000
Therefore, The median salary increases by $4,000
Learn more about mean and median: click this link
https://brainly.com/question/67180
#1234
A right angled triangle is formed by the diameters of three semicircular regions.
Answers
Area of region A is equal to the sum of area of region B and area of region C when a right-angled triangle is formed by the diameters of three semi-circular regions A, B, and C.
Let the diameters of semicircle A, B and C be a, b and c respectively.
We know area of a semi-circular region of diameter d is
A = (1/2)(πd²/4)
A = πd²/8
Thus,
area of region A is πa²/8
area of region B is πb²/8
area of region C is πc²/8
The triangle formed is a right angled triangle, with hypotenuse a and legs b and c. By Pythagoras theorem
a² = b² + c²
Multiplying both sides by π/8
(π/8)a² = (π/8)(b² + c²)
πa²/8 = πb²/8 + πc²/8
Area of region A = Area of region B + Area of region C
Hence proved.
--The question is incomplete, answering to the question below--
"A right-angled triangle is formed by the diameters of three semi-circular regions A, B, and C as shown in the diagram. Show that area of region A = area of region B + area of region C."
To know more on Pythagoras theorem
https://brainly.com/question/343682
#SPJ4

the dimensions of a high school football field are represented by a width of 2x - 40 feet and a length of 3x + 60 feet
what expression represents the binomial factors you would multiply to find the area of the football field?
Answers
(WORK SHOWN BELOW)

two angels are vertical angles. One angle is labeled 2x. the other angle is labeled (x+30). Find the value of x.
Answers
Answer:
x=30
Step-by-step explanation:
2x=x+30
x=30
A pair of walkie-talkies has a 35-meter range. Anand's apartment is 18 meters
east and 19 meters north of Isaac's apartment. Isaac's apartment is at sea
level, while Anand's apartment is 7 meters above sea level. Can they use the
walkie-talkies to talk to each other from their apartments?
, because the distance between their apartments is square root meters, or to the nearest tenth, meters.

Answers
Yes, they can use the walkie-talkies to talk to each other.
The distance between them is given as 28.2 meters.
How to solve for the distance?The horizontal and vertical distances should be considered when calculating the distance between their apartments using the three-dimensional form of the Pythagorean theorem.
This comes out as \(\sqrt((18^2 + 19^2 + 7^2))\), which equals \(\sqrt(798)\) square root meters, or, to the nearest tenth, 28.2 meters.
Since this distance is less than the 35-meter range of the walkie-talkies, communication should be possible between the two apartments.
Read more about distance here:
https://brainly.com/question/2854969
#SPJ1
The equation y+ 3 = 5(x - 3) represents a linear function. What is the y intercept of the equation?
Answers
Answer:
-18
Step-by-step explanation:
If you're looking for the y-intercept for this equation this means that x = 0.
So substitute x as 0 in the equation and you'll get the following.
y + 3 = 5 (0 - 3)
y + 3 = -15
y = -18
You need to compute the 99% confidence interval for the population mean. How large a sample should you draw to ensure that the sample mean does not deviate from the population mean by more than 1.3
Answers
To compute the 99% confidence interval for the population mean, you need to determine the appropriate sample size to ensure that the sample mean does not deviate from the population mean by more than 1.3. The key terms involved in this process are the confidence interval, sample size, population mean, and sample mean.
The confidence interval represents the range within which the population parameter (in this case, the population mean) is likely to fall, given a certain level of confidence. A 99% confidence interval means that you are 99% confident that the true population mean falls within the specified range.
To calculate the required sample size, you will need to use the formula for the margin of error (E), which is E = (Zα/2 * σ) / √n, where Zα/2 is the critical value associated with the desired level of confidence (99%), σ is the population standard deviation, and n is the sample size.
Since you want the sample mean to not deviate from the population mean by more than 1.3, you will need to set E = 1.3 and solve for n. After finding the critical value for a 99% confidence interval (which is approximately 2.576) and assuming you know the population standard deviation, you can plug these values into the formula and solve for n.
By doing this, you will be able to determine the appropriate sample size to ensure that the 99% confidence interval for the population mean is within 1.3 units of the sample mean.
To learn more about confidence interval click here
brainly.com/question/22851322
#SPJ11
One study indicates that each individual in the United States produces about 2 kg of solid waste per day. That figure is up from about 1.2 kg in 1960. Which is most responsible for the increase?
A more packaging
B denser solid waste
C more electronic devices
D increased food consumption
Answers
As per the unitary method, most responsible for the increase is more packing.
The term unitary method in math refers the process of finding the value of a single unit, and based on this value.
Here we have given that One study indicates that each individual in the United States produces about 2 kg of solid waste per day. That figure is up from about 1.2 kg in 1960.
And we need to find most responsible for the increase.
While we looking into the given question, we have identified that in 1960 the solid waste per day is 1.2 kg.
And the current solid waste per day is 2 kg.
Then the the difference between these two is calculated as,
=> 2 - 1.2
=> 0.8kg.
So, there is 800 gram of waste is increased and while looking into the given option, the resulting one is option (a).
To know more about Unitary method here.
https://brainly.com/question/28276953
#SPJ4
Write the equation of the line in slope-intercept form.

Answers
Answer:
y=5x-2
Step-by-step explanation:
What is the completely factored form of x4y – 4x2y – 5y? y(x2 – 5)(x2 1) y(x2 5)(x2 – 1) (x2y – 5)(x2 1) (x2y 5)(x2 – 1)
Answers
Answer:
y (x² + 1) (x² - 5)
Step-by-step explanation:
Factorization:Take 'y' from each term.
x⁴y - 4x²y - 5y = y[x⁴ - 4x² - 5]
Now factorize x⁴ - 4x² - 5.
Sum = -4
Product = -5
Factors = -5 , 1
When we add (-5) + 1, it gives (-4) and when we multiply (-5)*1, gives (-5).
x⁴ - 4x² - 5 = x⁴ + x² - 5x² - 5
= x²(x² + 1) -5(x² + 1)
= (x²+ 1) (x² - 5)
x⁴y - 4x²y - 5y = y (x² + 1) (x² - 5)
The midday temperature in Palm
Beach was 86 °F. The
temperature then
changed 2 °F per hour for the next
3 hours. The expression 86 -|-2-3|
represents the current temperature.
What is the current temperature in
degrees Fahrenheit?
Answers
After considering all the given data we conclude that the current measured temperature in degree Fahrenheit is 91°F, under the condition that the midday temperature in Palm Beach was 86 °F and the given expression is 86 -|-2-3| which represents current temperature.
To evaluate the temperature let us first consider the expression 86 -|-2-3| which represents the current temperature after 3 hours of temperature change of 2°F per hour from an initial temperature of 86°F.
The given expression can be again simplified as
86 -|-2-3| = 86 -|-5|
= 86 - (-5)
= 91°F
Hence, after evaluating we finally measured the current temperature as 91°F.
To learn more about Fahrenheit
https://brainly.com/question/30391112
#SPJ1
what is the value of 10x^3 y^2 when x=-2 and y=-3
Answers
Answer:
-720
Step-by-step explanation:
We are given the expression:
\(10x^3y^2\)
and asked to evaluate when x= -2 and y= -3.
Therefore, we must substitute -2 for x and -3 for y.
\(10(-2)^3*(-3)^2\)
Solve according to PEMDAS: Parentheses, Exponents, Multiplication, Division, Addition, Subtraction.
Evaluate the first exponent.
⇒ (-2)³ = -2 * -2 * -2= 4*-2= -8
\(10(-8)*(-3)^2\)
Evaluate the second exponent.
⇒ (-3)²= -3 * -3= 9
\(10(-8)*9\)
Multiply 10 and -8.
\(-80*9\)
Multiply -80 and 9.
\(-720\)
The value of 10x³y² at x= -2 and y= -3 is -720

−2 + x ≤ −16 a closed or open circle?
Answers
Answer:
Closed circle
Step-by-step explanation:
If the sign is less than or equal too/greater than or equal too the circle will be closed
Answer:
closed
Step-by-step explanation:
use an open circle for "less than" or "greater than", and a closed circle for "less than or equal to" or "greater than or equal to".
Anyone can help me with math for solving for a side in the right triangles for khan academy

Answers
Answer:
7.45
Step-by-step explanation:
We are given a right triangle with one side length known and an angle know so we can use some trigonometry.
You need to find the hypotenuse so you are going to use either sine or cosine.
Since the adjacent from the angle is given (SOH-CAH-TOA) we can use cosine so,
cos(20) = 7/h
=>h = 7/cos(20)
=> 7.44924
=> 7.45
I'm having a really hard time on this question and it's really late I just want to get this done

Answers
Answer:
48cm³
Step-by-step explanation:
volume = (7 X 6 X 1) + (3 X 2 X 1)
= (42 + 6)
= 48cm³
The team won 16 games, lost 6 games and tied 2 games. What percent of the games did the team win?
Answers
Answer:
66% or 2/3
Step-by-step explanation:
add all the games up and you get 24 games played total then divide 16 by 24 and you get .66 or 2/3 because 16 is 2/3 of 24 and they are both a multiple of 8
16 mi c. john started a carpool with his coworkers to save money. he and his three passengers split the cost of the toll. if each person pays about $0.81 , which includes their contribution to the toll lane entry fee, how many miles do they travel on the toll lane?
Answers
John and his three passengers travel a total of 20.25 miles on the toll lane.
To solve this problem, we can use the fact that each person pays about $0.81, which includes their contribution to the toll lane entry fee. This means that the total amount of money paid by John and his three passengers is 4 times $0.81, or $3.24.
We can then use this information to find the cost per mile of the toll lane. If they traveled a total of x miles on the toll lane, then the cost per mile would be:
$3.24 / x
We can set this equal to the given cost of 16 cents per mile:
$0.16 = $3.24 / x
Multiplying both sides by x, we get:
x * $0.16 = $3.24
Dividing both sides by $0.16, we get:
x = $3.24 / $0.16
x = 20.25 miles
In summary, to find the distance they traveled on the toll lane, we used the fact that they split the cost of the toll, and that each person paid about $0.81. We then set the cost per mile equal to the given cost of 16 cents per mile, and solved for the distance traveled on the toll lane, which turned out to be 20.25 miles.
To learn more about miles click on,
https://brainly.com/question/30298989
#SPJ4
Please answer I’ll give brainliest.
I want the answers for the holes of the function when solved and the end behavior it has when x is going to negative and positive.

Answers
Answer:
\(f(x) = \frac{ {x}^{2} + x - 6 }{x + 2} = \frac{(x + 3)(x - 2)}{x + 2} \)
There are no holes in this function.
As x-->negative infinity, f(x)-->negative infinity.
As x-->infinity, f(x)-->infinity.