Write the product (2x - 5)² in the form az²+bx+c and identify the values of a, b, and c. Type numerical values only. No variables
ANSWER FAST FOR LOTS OF POINTS

Answers
The product of (2x - 5)² can be written in the form az²+bx+c as follows:
(2x - 5)² = (2x)² - 2(2x)(5) + (5)²
= 4x² - 20x + 25
In this expression, a = 4, b = -20, and c = 25.
Related Questions
The number of ways of arranging all trials to be failures in a binomial distribution is:?
Answers
In a binomial distribution, the number of ways of arranging all trials to be failures is 1. This means that there is only one way to have all trials result in failures, as each trial can only have one possible outcome - a failure.
1. In a binomial distribution, each trial can result in either a success or a failure. Let's assume that there are n trials in total.
2. To arrange all trials to be failures, we need to ensure that no trial results in a success. Therefore, for each trial, there is only one possible outcome - a failure.
3. The number of ways of arranging all trials to be failures can be calculated using combinations. In this case, we need to select 0 successes from n trials. The number of ways to do this is given by the combination formula: C(n, 0) = 1, where C represents the combination.
Therefore, the number of ways of arranging all trials to be failures in a binomial distribution is given by the combination formula, C(n, k) = n! / (k! * (n-k)!).
To know more about binomial distribution visit:
https://brainly.com/question/29137961
#SPJ11
The number of ways of arranging all trials to be failures in a binomial distribution is always 1. This is because there is only one way to have no successes in a set of trials.
Regardless of the number of trials or the probability of success, the number of ways of arranging all trials to be failures in a binomial distribution is always 1.
The number of ways of arranging all trials to be failures in a binomial distribution can be determined using the formula for the binomial coefficient.
The binomial coefficient, often denoted as nCk or n choose k, represents the number of ways to choose k items from a set of n items, without considering their order. In the context of a binomial distribution, n represents the total number of trials and k represents the number of successes (in this case, 0).
To find the number of ways of arranging all trials to be failures, we can use the binomial coefficient formula:
nCk = n! / (k!(n-k)!)
In this case, since we want all trials to be failures, k is equal to 0. Thus, the formula simplifies to:
nC0 = n! / (0!(n-0)!) = n! / (0! * n!) = 1
For example, if we have 5 trials and we want all of them to be failures, there is only one possible arrangement: FFFFF, where F represents a failure.
Learn more about probability from the given link:
https://brainly.com/question/13604758
#SPJ11
which provides a better estimate of the theoretical probability p(h) for the unfair coin: an empirical probability using 30 flips or 1000 flips? why do you think so?
Answers
the empirical probability based on 1000 flips provides a better estimate of the theoretical probability p(h) for the unfair coin.
The empirical probability is based on observed data from actual trials or experiments. It involves calculating the ratio of the number of favorable outcomes (e.g., getting a "heads") to the total number of trials (flips). The larger the number of trials, the more reliable and accurate the estimate becomes.
When estimating the theoretical probability of an unfair coin, it is important to have a sufficiently large sample size to minimize the impact of random variations. With a larger number of flips, such as 1000, the estimate is based on more data points and is less susceptible to random fluctuations. This helps to reduce the influence of outliers and provides a more stable and reliable estimate of the true probability.In contrast, with only 30 flips, the estimate may be more affected by chance variations and may not fully capture the underlying probability of the coin. Therefore, the empirical probability based on 1000 flips provides a better estimate of the theoretical probability p(h) for the unfair coin.
Learn more about empirical here:
https://brainly.com/question/27709173
#SPJ11
Answer:
Experimental probability
Step-by-step explanation:
Experimental probability is a probability that is determined on the basis of a series of experiments. A random experiment is done and is repeated many times to determine their likelihood and each repetition is known as a trial.
Molly is making a scale drawing of her bedroom. The length of the room is 1.2 times the width. If Molly’s drawing is 15 inches long, how wide is the drawing?
Answers
The Answer: Is 13.8 Inches Wide
Step-by-step explanation: The reason how i got this answer is because you have to Subtract 1.2-15 Witch = -13.8 But you got to take the negative of the 13.8 And that's how i got this answer. (:
Answer:
15 divided by 1.2= 12.5
Step-by-step explanation:
This is the correct answer because if you guys r doing the savvas realize this is the answer that I got and it was correct :D
n the dilation shown above, the dark-colored figure represents the original image and the light-colored figure represents the resulting image.
What is the scale factor for this dilation?
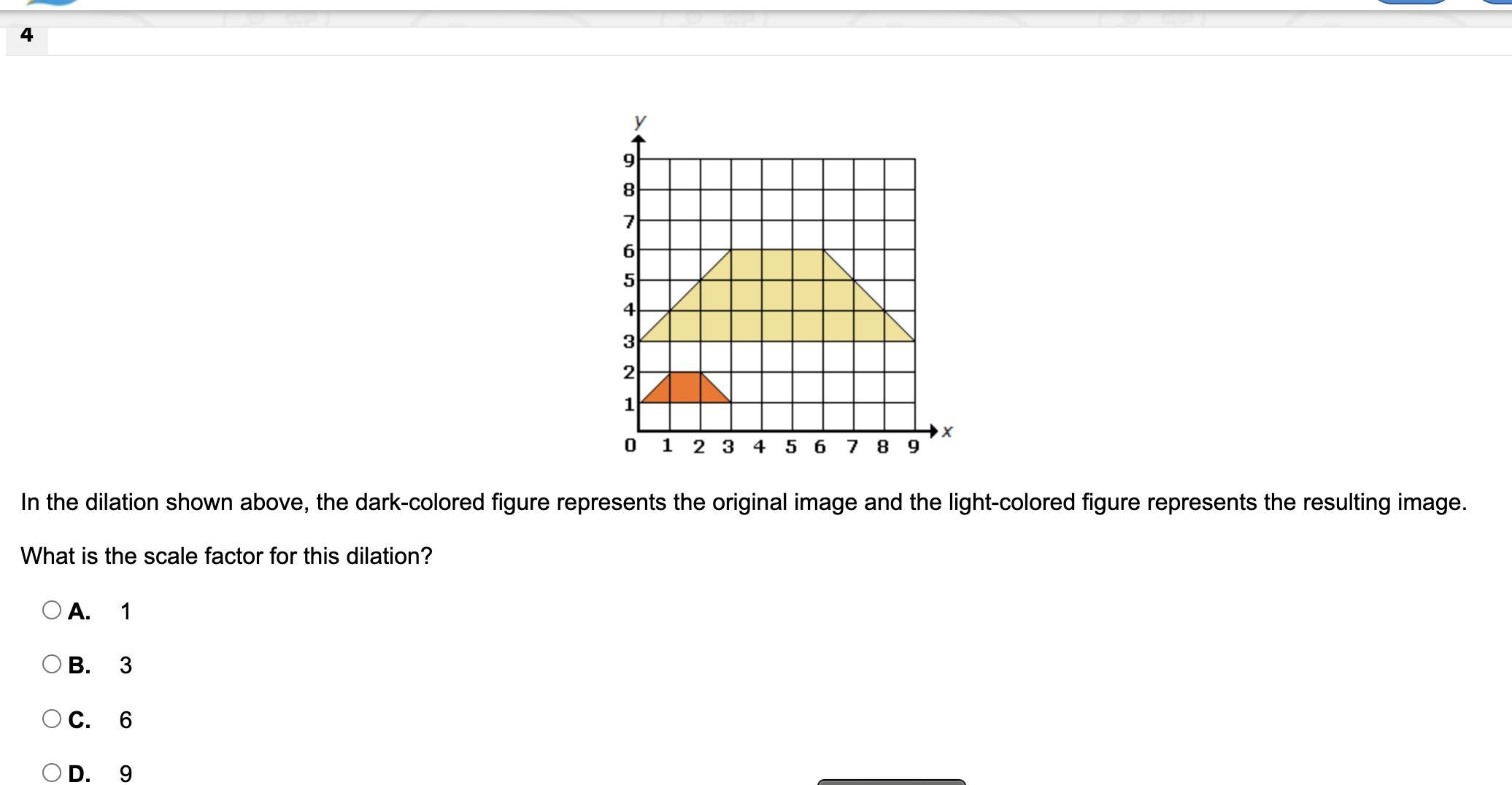
Answers
The scale factor used in the dilation is 3
Determining the scale factor used.From the question, we have the following parameters that can be used in our computation:
Image = 9
Pre-image = 3
The scale factor is calculated as
Scale factor = Image/Pre-Image
Substitute the known values in the above equation, so, we have the following representation
Scale factor = 9/3
Evaluate
Scale factor = 3
Hence, the scale factor is 3
Read more about scale factor at
brainly.com/question/29229124
#SPJ1
you intend to estimate a population mean with a confidence interval. you believe the population to have a normal distribution. your sample size is 15. find the critical value that corresponds to a confidence level of 90%. (report answer accurate to three decimal places with appropriate rounding.)
Answers
The critical value that corresponds to a confidence level of 90 % [1.34503037 , ∞ ).
Given:
you intend to estimate a population mean with a confidence interval. you believe the population to have a normal distribution. your sample size is 15. find the critical value that corresponds to a confidence level of 90%.
sample size n = 15
confidence interval ci = 90
we know that,
Degrees of freedom df = n - 1
here n = 15
df = n - 1
= 15 - 1
= 14
Using the graphical t value calculator:
with df = 14 significance level = 1 - 0.90 = 0.10
so t = [1.34503037 , ∞ )
Learn more about the normal distribution here:
https://brainly.com/question/29509087
#SPJ4
Graphs. For the function f(x)=(x+11)(x−1)²(x−2)(x−3)(x-4)+6.107
find numeric approximations (round to three decimal places) for the following features. For this problem you do not need to explain your process; simply report your numeric estimates.
a) Coordinates of the y-intercept:
b) x-intercepts (there are six):
c) Range:
Answers
a) Y-intercept: To find the y-intercept, substitute x = 0 into the function equation and calculate the corresponding y-value. The y-intercept will have the coordinates (0, y).
b) X-intercepts: To find the x-intercepts, set the function equal to zero (f(x) = 0) and solve for x. The solutions will give the x-values where the function intersects the x-axis. Each x-intercept will have the coordinates (x, 0).
c) Range: To determine the range, analyze the behavior of the function and identify any restrictions or limitations on the output values. Look for any values that the function cannot attain or any patterns that suggest a specific range.
a) Coordinates of the y-intercept:
The y-intercept occurs when x = 0. Substitute x = 0 into the function:
f(0) = (0+11)(0-1)²(0-2)(0-3)(0-4) + 6.107 = 11(-1)²(-2)(-3)(-4) + 6.107 = 11(1)(-2)(-3)(-4) + 6.107
Calculating this expression gives us the y-coordinate of the y-intercept.
b) x-intercepts (there are six):
To find the x-intercepts, we need to solve the equation f(x) = 0. Set the function equal to zero and solve for x. There may be multiple solutions.
c) Range:
The range of the function represents all possible y-values that the function can take. To find the range, we need to determine the minimum and maximum values that the function can attain. This can be done by analyzing the behavior of the function and finding any restrictions or limitations on the output values.
learn more about "Range":- https://brainly.com/question/10197594
#SPJ11
Q. What is the measure of BOC

Answers
Answer:
142 i think
Step-by-step explanation:
180-38=142
Find the Area! Need help asap

Answers
Answer:
5.6ft squared
Step-by-step explanation:
4x7 = 28 divided by 5 which is 5.6
Find the slope of the line represented by each table of values

Answers
Answer:
slope is zero
Step-by-step explanation:
every y=9 then the line is parallel to x axiom
One number exceed another by 11, the sum of the two numbers is 5. What are the numbers?
Answers
Answer:
The first number is -3, the second number is 8
Step-by-step explanation
Let x = the first number
exceeded means add, so the second number is x+11
sum means add, so the equation is x+x+11=5
combine like terms to get 2x+11=5
subtract 11 on both sides, 2x=-6
divide by 2 on both sides, x= -3
second number was x+11, so -3+11 = 8
Question 7
The perimeter of the rectangle Is 34 inches. The perimeter of the triangle is
40 Inches.
Answers
Answer:
whts the question 86
Step-by-step explanation:
i dk
Question 83 pts
Given that 2 Al + 6 HCl → 2 AlCl3 + 3H2
UR ON TIMER GO FASTtt How many moles of hydrogen are produced if we start from 2.2 mol Al and 4.2 mol HCl?
2.1
mol H2
How many moles of excess reactant are left over?
Answers
Answer:
Ummm I dont know what subject it is so i will guess 2.3?
Step-by-step explanation:
I'm Sorry im really useless
Which equation represents the proportional relationship between the cost, t, in dollars, of p pounds of wood bought? T=0.29pt = 0.29 p t=0.31pt = 0.31 p t=3.45pt = 3.45 p t=3.48p
Answers
Answer:
T = 0.29p
Step-by-step explanation:
From the table Given :
We can obtain the uint cost per pound of wood :
Cost of 12 pounds of wood = $3.48
Cost per pound = Cost / weight
Cost per pound = $3.48 / 12 = $0.29
Hence, the proportional relationship cost, T in dollars and p pounds of wood is ;
Cost = unit cost per pound * number of pounds
T = 0.29 * p
T = 0.29p

pls help i dont understand

Answers
The linear function giving the amount remaining after buying x cups of coffee is given as follows:
A(x) = -3x + 15.
How to obtain a linear function?
The slope-intercept definition of a linear function is given as follows:
y = mx + b.
In which:
The slope m represents the rate of change.The intercept b represents the value of y when x = 0.Each cup of coffee costs $3, hence the slope m is given as follows:
m = -3.
(for each cup purchased, the balance decays by $3).
Hence:
A(x) = -3x + b.
Buying 4 cups of coffee, the balance is of $3, hence the intercept b is obtained as follows:
3 = -3(4) + b
b = 15.
More can be learned about linear functions at https://brainly.com/question/24808124
#SPJ1
Solve: (7+5i) + n =0, what's n? What
property is this?
Hurry please need it.

Answers
Answer:
n = -7-5i
Step-by-step explanation:
This is the inverse property of addition
Answer plzz I give will correct answer as brainliest

Answers
Answer: 13m
Step-by-step explanation:
A^2+ B^2= C^2
5^2+ 12^2= c^2
169= C^2
then square root the 169 to get 13
according to a major credit card company, the mean outstanding credit card debt of college undergraduates was $2,683 in 2006, with a standard deviation of $40. what test statistic is calcuated for this scenario?
Answers
The scenario of the test statistic by assuming observed value as 2800 for the given mean of $2.683 is equal to 2.925.
Mean of debt of college graduates in 2006 = $2,683
Standard deviation = $40.
To calculate the test statistic, we need to have a hypothesis test.
The z-score for a particular value of outstanding credit card debt.
The formula for calculating the z-score is,
z = (x - μ) / σ
where
x is the observed value,
μ is the mean,
and σ is the standard deviation.
Let us assume to calculate the z-score for a college undergraduate who has an outstanding credit card debt of $2,800.
Then, the z-score will be,
z = (2800 - 2683) / 40
= 2.925
Therefore, the test statistic of z-score for this scenario is 2.925 by assuming outstanding credit card debt value as $2,800.
Learn more about test statistic here
brainly.com/question/16986736
#SPJ4
Helppppppp with this question quick

Answers
Answer:
c
Step-by-step explanation:
Which expression is equivalent to
(3m² + 5m - 2) + (-2m +18)?
Someone answer ASAP
Answers
3m^2 +5m-2-2m+18
3m^2 +3m+16
Answer:
3m² + 3 m + 16
Step-by-step explanation:
( 3 m ² + 5 m - 2 ) + ( - 2m + 18 )
Remove the unnecessary parantheses and rewrite
3 m ² + 5 m - 2 - 2 m + 18
combine like terms
3m² + 5 m - 2 m + 18 - 2
calculate the sum
3m² + 3 m + 16
A roller-coaster car moves 200ft horizontally and then rises 135ft at an angle of 30.0
∘
above the horizontal. It next travels 135ft at an angle of 40.0
∘
downward. What is its displacement from its starting point? Use graphical techniques.
Answers
The displacement of the roller-coaster car from its starting point can be determined using graphical techniques. The main answer is that the displacement is approximately 157.5 ft in magnitude and in the direction opposite to the car's initial motion.
To explain further, we can break down the motion into horizontal and vertical components. The car initially moves 200 ft horizontally, which means its horizontal displacement is 200 ft. Then, it rises 135 ft at an angle of 30.0° above the horizontal. This vertical displacement can be calculated as 135 ft * sin(30.0°) = 67.5 ft upward.
Next, the car travels 135 ft at an angle of 40.0° downward. This contributes to a vertical displacement of 135 ft * sin(40.0°) = 87.2 ft downward.
To find the total vertical displacement, we subtract the downward displacement from the upward displacement: 67.5 ft - 87.2 ft = -19.7 ft.
Finally, we can use the Pythagorean theorem to calculate the magnitude of the displacement. The horizontal displacement is 200 ft and the vertical displacement is -19.7 ft. So, the magnitude of the displacement is sqrt((200 ft)^2 + (-19.7 ft)^2) ≈ 157.5 ft.
Since the vertical displacement is negative, the displacement is in the direction opposite to the initial motion of the car.
Learn more about Pythagorean theorem here:
brainly.com/question/14930619
#SPJ11
What is the mole of H2?
Answers
One mole of H2 contains 6.022 x 10^23 H2 molecules. This can be used to calculate the number of H2 molecules in a given volume or mass of hydrogen gas.
What is mole?A mole is a unit of measurement in chemistry that expresses the amount of a substance. It is defined as the number of entities (such as atoms, ions, or molecules) in a sample of the substance. The number of entities in one mole of a substance is known as Avogadro's number.
What is Avogadro's number?Avogadro's number is a fundamental constant of physics and chemistry, defined as the number of atoms, ions or molecules in one mole of substance. It is approximately 6.022 x 10^23 and is used in many calculations in chemistry and physics, such as the number of atoms in a sample of an element, the number of ions in a salt, or the number of molecules in a gas sample. The constant is named after Amedeo Avogadro, an Italian scientist who first proposed the concept in 1811.
One mole of a substance is equal to Avogadro's number, which is approximately 6.022 x 10^23.
The mole of H2 (hydrogen gas) is the number of H2 molecules in a sample of hydrogen gas. One mole of H2 contains 6.022 x 10^23 H2 molecules. This can be used to calculate the number of H2 molecules in a given volume or mass of hydrogen gas.
To know more about mole visit:
https://brainly.com/question/26416088
#SPJ4
Under which circumstance can a very small treatment effect still be statistically significant?
Answers
If the sample size is small and the sample variance is large then
small treatment effect still be statistically significant.
As we know that,
Statustical significance refers to claim that a result from data generated by testing or experimentation is likely to be attributable to specific cause.
Sample size is the total number of individuals or items that comprise a sample.
And, the variance is a descriptive statistic, which falls under the category of a measure of spread.
The circumstance in which a very small treatment effect can be found to be significant is best described by option A: If the sample size big and the sample variance is small.
A large sample size will increase the probability that the results of a statistical test will yield significant results. This is why most statistical tests are accompanied by a measure of effect size. A statistically significant result associated with a very large sample size, will likely have a small effect size, an undesirable result for a researcher, as it implies one of the only reasons significant results were obtained was due to the large sample, not necessary the magnitude of the experimental effect.
Likewise, if variance is small, this will also increase the probability that the results of a statistical test will yield significant results. Variance is simply another word in statistics for the error. A decrease in error will lead to an increased probability of obtaining significant results, hence the idea that a small amount of variance will lead to an increased probability of significant results.
Hence, if the sample size is small and the sample variance is large then
small treatment effect still be statistically significant.
Find out more information about statistical significance here:
https://brainly.com/question/14100967
#SPJ4
What sample size is needed to obtain a 90 percent confidence interval for the mean protein content of meat if the estimate is to be within 2 pounds of the true mean value? Assume that the variance is 49 pounds.
Answers
Thus, we need a sample size of at least 22 to obtain a 90 percent confidence interval for the mean protein content of meat with an estimate within 2 pounds of the true mean value.
To obtain a 90 percent confidence interval for the mean protein content of meat with an estimate within 2 pounds of the true mean value, we need to calculate the required sample size. The formula for the required sample size is:
n = (Zα/2 * σ / E)^2
where n is the required sample size, Zα/2 is the z-score for the desired confidence level (in this case 90%), σ is the standard deviation of the population (in this case 7 pounds, the square root of the variance), and E is the margin of error (in this case 2 pounds).
Plugging in the values, we get:
n = (1.645 * 7 / 2)^2
n = 21.16
Therefore, we need a sample size of at least 22 to obtain a 90 percent confidence interval for the mean protein content of meat with an estimate within 2 pounds of the true mean value. It is important to note that this assumes that the sample is drawn randomly and is representative of the population.
Know more about the confidence interval
https://brainly.com/question/20309162
#SPJ11
Find the volume of the solid of intersection of the two right circular cylinders of radius r whose axes meet at right angles.
Answers
The solid of intersection of the two right circular cylinders of radius r whose axes meet at right angles is known as a Steiner's Reversed Cycloid. It has a volume of V=16πr³/9. The intersection volume between two identical cylinders whose axes meet at right angles is called a Steiner solid (sometimes also referred to as a Steinmetz solid).
To find the volume of a Steiner solid, you must first define the radii of the two cylinders. The radii of the cylinders in this question are r. You must now compute the volume of the solid formed by the intersection of the two cylinders, which is the Steiner solid.
A method for determining the volume of the Steiner solid formed by the intersection of two cylinders whose axes meet at right angles is shown below. You can use any unit of measure, but be sure to use the same unit of measure for each length measurement. V=16πr³/9 is the formula for finding the volume of the Steiner solid for two right circular cylinders of the same radius r and whose axes meet at right angles. You can do this by subtracting the volumes of the two half-cylinders that are formed when the two cylinders intersect. The height of each of these half-cylinders is equal to the diameter of the circle from which the cylinder was formed, which is 2r. Each of these half-cylinders is then sliced in half to produce two quarter-cylinders. These quarter-cylinders are then used to construct a sphere of radius r, which is then divided into 9 equal volume pyramids, three of which are removed to create the Steiner solid.
Volume of half-cylinder: V1 = 1/2πr² * 2r
= πr³
Volume of quarter-cylinder: V2 = 1/4πr² * 2r
= πr³/2
Volume of sphere: V3 = 4/3πr³
Volume of one-eighth of the sphere: V4 = 1/8 * 4/3πr³
= 1/6πr³
Volume of the Steiner solid = 4V4 - 3V2
= (4/6 - 3/2)πr³
= 16/6 - 9/6
= 7/3πr³
= 2.333πr³ ≈ 7.33r³ (in terms of r³)
To know more about right angles visit :
https://brainly.com/question/3770177
#SPJ11
In November's Math Meet, the Little Monsters of Beast Academy solved $\frac{1}{5}$ of the problems. In March's Math Meet, they solved $\frac23$ of the problems. (There might be different numbers of problems asked in November and March.)
In total, the Little Monsters solved $13$ of $30$ problems over both Math Meets. How many problems were asked at March's Math Meet?
Answers
The Little Monsters of Beast Academy completed 15 problems during the math meet in March.
How to calculate the total number of issues resolved in MarchThe issue is a simultaneous equation involving two equations and two unknowns.
These are the equations that are created:
Let the quantity of questions that the students at the Beast Academy have answered in
March be xNovember be yThe Little Monsters of Beast Academy successfully completed $frac1/5$ of the problems in the November = y/5
In Math Meet. they resolved $frac23$ = 2x/3 problems i
Hence:
y/5 + 2x/3 = 12
x + y = 30
When the equation is solved,
x = y = 15
Learn more on simultaneous equation here:
brainly.com/question/15165519
#SPJ1
Function 1: y = 4x + 5 Function 2: The line passing through the points (1, 6) and (3, 10). Which of these functions has the greater rate of change? Responses A Function 2, because the slope is 5 and the slope of function 1 is 4.Function 2, because the slope is 5 and the slope of function 1 is 4. B Function 2, because the slope is 7 and the slope of function 1 is 5.Function 2, because the slope is 7 and the slope of function 1 is 5. C Function 1, because the slope is 4 and the slope of function 2 is 2.Function 1, because the slope is 4 and the slope of function 2 is 2. D Function 1, because the slope is 5 and the slope of function 2 is 4
Answers
The line y = 4x + 5 has, Function 1, because the slope is 4 and the slope of function 2 is 2.
What are lines and their slopes?We know lines have various types of equations, the general type is
Ax + By + c = 0, and the equation of a line in slope-intercept form is
y = mx + b.
Where slope = m and b = y-intercept.
the slope is the rate of change of the y-axis with respect to the x-axis and the y-intercept is the (0,b) where the line intersects the y-axis at x = 0.
Given, y = 4x + 5 which is an equation of a line.
Another line passes through points (1, 6) and (3, 10).
Therefore, slope(m) = (10 - 6)/(3 - 1).
slope(m) = 4/2 = 2.
Now, 10 = 2(3) + b.
b = 4.
So, The required line is y = 2x + 4.
Now, The line y = 4x + 5 has greater rate of change as the modulus value of slope is greater.
learn more about lines and slopes here :
https://brainly.com/question/3605446
#SPJ1
Graph the circle (2x - 3)2 + (y + 3)2 =36
Answers
Answer: 9 on the x axis and 18 on the y axis
Answer:
\(\mathrm{Ellipse\:with\:center}\:\left(h,\:k\right)=\left(\frac{3}{2},\:-3\right),\:\:\mathrm{semi-major\:axis}\:b=6,\:\:\mathrm{semi-minor\:axis}\:a=3\)
Step-by-step explanation:
\(\left(2x-3\right)^2+\left(y+3\right)^2=36\\\frac{\left(x-h\right)^2}{a^2}+\frac{\left(y-k\right)^2}{b^2}=1\:\mathrm{is\:the\:ellipse\:standard\:equation}\\\mathrm{with\:center}\:\left(h,\:k\right)\:\mathrm{and\:}a,\:b\mathrm{\:are\:the\:semi-major\:and\:semi-minor\:axes}\\\mathrm{Rewrite}\:\left(2x-3\right)^2+\left(y+3\right)^2=36\:\mathrm{in\:the\:form\:of\:the\:standard\:ellipse\:equation}\\\left(2x-3\right)^2+\left(y+3\right)^2=36\\\mathrm{Rewrite\:as}\\\left(2x-3\right)^2+\left(y+3\right)^2-36=0\)
\(\mathrm{Simplify}\:\left(2x-3\right)^2+\left(y+3\right)^2-36:\quad 4x^2-12x+y^2+6y-18\\4x^2-12x+y^2+6y-18=0\\\mathrm{Add\:}18\mathrm{\:to\:both\:sides}\\4x^2-12x+y^2+6y=18\\Factor\:out\:coefficient\:of\:square\:terms\\4\left(x^2-3x\right)+\left(y^2+6y\right)=18\\\mathrm{Divide\:by\:coefficient\:of\:square\:terms:\:}4\\\left(x^2-3x\right)+\frac{1}{4}\left(y^2+6y\right)=\frac{9}{2}\\\mathrm{Divide\:by\:coefficient\:of\:square\:terms:\:}1\)
\(\frac{1}{1}\left(x^2-3x\right)+\frac{1}{4}\left(y^2+6y\right)=\frac{9}{2}\\\mathrm{Convert}\:x\:\mathrm{to\:square\:form}\\\frac{1}{1}\left(x^2-3x+\frac{9}{4}\right)+\frac{1}{4}\left(y^2+6y\right)=\frac{9}{2}+\frac{1}{1}\left(\frac{9}{4}\right)\\\mathrm{Convert\:to\:square\:form}\\\frac{1}{1}\left(x-\frac{3}{2}\right)^2+\frac{1}{4}\left(y^2+6y\right)=\frac{9}{2}+\frac{1}{1}\left(\frac{9}{4}\right)\\\mathrm{Convert}\:y\:\mathrm{to\:square\:form}\)
\(\frac{1}{1}\left(x-\frac{3}{2}\right)^2+\frac{1}{4}\left(y^2+6y+9\right)=\frac{9}{2}+\frac{1}{1}\left(\frac{9}{4}\right)+\frac{1}{4}\left(9\right)\\\mathrm{Convert\:to\:square\:form}\\\frac{1}{1}\left(x-\frac{3}{2}\right)^2+\frac{1}{4}\left(y+3\right)^2=\frac{9}{2}+\frac{1}{1}\left(\frac{9}{4}\right)+\frac{1}{4}\left(9\right)\\\mathrm{Refine\:}\frac{9}{2}+\frac{1}{1}\left(\frac{9}{4}\right)+\frac{1}{4}\left(9\right)\\\frac{1}{1}\left(x-\frac{3}{2}\right)^2+\frac{1}{4}\left(y+3\right)^2=9\)
\(\mathrm{Divide\:by}\:9\\\frac{\left(x-\frac{3}{2}\right)^2}{9}+\frac{\left(y+3\right)^2}{36}=1\\\mathrm{Rewrite\:in\:standard\:form}\\\frac{\left(x-\frac{3}{2}\right)^2}{3^2}+\frac{\left(y-\left(-3\right)\right)^2}{6^2}=1\\\mathrm{Therefore\:ellipse\:properties\:are:}\\\left(h,\:k\right)=\left(\frac{3}{2},\:-3\right),\:a=3,\:b=6\\b>a\:\mathrm{therefore}\:b\:\mathrm{is\:semi-major\:axis\:and}\:a\:\mathrm{is\:semi-minor\:axis}\)
\(\mathrm{Ellipse\:with\:center}\:\left(h,\:k\right)=\left(\frac{3}{2},\:-3\right),\:\:\mathrm{semi-major\:axis}\:b=6,\:\:\mathrm{semi-minor\:axis}\:a=3\)
the minimax regret criterion is also referred to by economists as:
Answers
The minimax regret criterion, also known as the minimax regret strategy, is an approach used in decision theory by economists. It aims to minimize the maximum regret that could be experienced when choosing a particular course of action.
The minimax regret criterion is a decision-making technique that takes into account the potential regret associated with each possible decision. It recognizes that decision-makers often face uncertainty and that their choices may lead to outcomes that are different from what was initially expected. By considering the worst-case scenario or maximum regret for each decision, the minimax regret criterion helps decision-makers select the option that minimizes the potential regret.
In this approach, decision-makers evaluate the consequences of their choices by comparing the actual outcome with the best outcome that could have been achieved if a different decision had been made. The minimax regret strategy focuses on minimizing the maximum regret across all possible decisions, aiming to choose the option that would result in the least regret, regardless of the actual outcome.
Economists often use the minimax regret criterion to analyze decision problems under uncertainty, particularly when the consequences of different actions cannot be precisely predicted. It provides a framework for decision-making that incorporates risk aversion and the desire to minimize the potential for regret. By considering the worst possible outcomes, decision-makers can make more informed choices that take into account the potential regrets associated with their decisions.
Learn more about outcomes here:
https://brainly.com/question/17238771
#SPJ11
Someone please help me with this math problem?

Answers
11. a bag contains 8 red marbles, 9 yellow marbles, and
7 green marbles. how many additional red marbles
must be added to the 24 marbles already in the bag so
that the probability of randomly drawing a red marble
is
15.
a 11
b. 16
c. 20
d. 24
e. 32
Answers
To get a probability of 3/5, 16 red marbles must be added.
How many additional red marbles must be added?
There are 8 red, 9 yellow, and 7 green marbles, for a total of:
8 + 9 + 7 = 24.
The probability of getting a particular color of marble is given by the quotient between the number of marbles of that color and the total number of marbles.
Here, we want to get a probability of drawing a red marble equal to 3/5.
So, if we add x red marbles, the probability of getting a red marble will be:
P = (8 + x)/(24 + x)
And that must be equal ot 1/5, then we write:
(3/5) = (8 + x)/(24 + x)
If we multiply both sides bt (24 + x), we will get:
3*(24 + x)/5 = 8 + x
Now we can solve that for x.
3*24/5 - 8 = x - x(3/5) = (2/5)*x
x = (3*24/5)*(5/2) - (5/2)*8 = 16
So 16 red marbles must be added, the correct option is b.
If you want to learn more about probability, you can read:
https://brainly.com/question/251701
#SPJ1