Write the product 5x2/3 as the product of a whole number and a unit fraction

Answer:

3

Step-by-step explanation:

12 times 3 = 36

36 times 6 = 216

12(x times 6)

(12)6x

72x

216 = 72x

216/72 = 3

Answer:

The number 3 makes this statement true.

\(x=3\)

Step-by-step explanation:

Given the equation:

\((12*3)*6=12*(x*6)\)

Using the order of operations, we can evaluate the terms in the parentheses through the process of multiplication:

\(36*6=12*6x\)

Multiply the terms on both sides of the equation:

\(216=72x\)

Finally, divide both sides of the equation by the coefficient of \(x\), which is \(72\):

\(3=x\)

\(x=3\)

-

Let's check our work by substituting the solved \(x\) value for

\((12*3)*6=12*(3*6)\)

\(36*6=12*18\)

\(216=216\)

Since both sides of the equation are equal to each other, our solution is correct!

The table of ordered pairs is completed below

Here is the completed table and plotted points:

Point x y (x,y)

A 4 9 (4,9)

B 6 3 (6,3)

C 1 3 (1,3)

D 8 7 (8,7)

E 8 9 (8,9)

To plot these ordered pairs on a coordinate plane, we need to draw the x and y axes, and label the units on each axis.

Then we can plot each point by starting at the origin (0,0) and moving horizontally (to the right if x is positive, or to the left if x is negative) and vertically (up if y is positive, or down if y is negative) to the corresponding point.

The points plotted on the coordinate plane are attached

Read more about coordinates at

https://brainly.com/question/30587266

#SPJ1

Complete the table. Then, plot the ordered pairs on the coordinate plane. Make sure to label each point with its corresponding letter.

              x                y       (x, y)

A            4                9

B            6                3

C            1                3

D            8                7

E             8                9

Answer:

a. 14

b. 28

Step-by-step explanation:

a. ex: (6+3)2 - 4 = 9(2) - 4

18 - 4 = 14

b. ex: 23 + (14 - 4) / 2

Use PEMDAS

P 1st

10

D over A

5

A

28

Hope this helps!

Answer:

220 student all together im not sure

Step-by-step explanation:

The rate at which the angle the ladder makes with the ground is changing when the ladder reaches 9 ft up the wall is 1 / (27 sec θ) ft/min.

Given Information:Ladder = 18 ft
Rate of Change of Ladder = 3 minutes
Height of ladder up the wall = 9 ft
To find: The rate at which the angle the ladder makes with the ground is changing
When the ladder reaches 9 ft up the wall, we need to find the rate at which the angle the ladder makes with the ground is changing.
In other words, we need to find the derivative of the angle that the ladder makes with the ground with respect to time.
Let's represent the angle the ladder makes with the ground by θ.
Let AB be the ladder and AC be the wall.
Let θ be the angle that the ladder AB makes with the ground.
Let x be the distance from the foot of the ladder to the wall.
Then, tan θ = x / 9 ft
=> x = 9 tan θ ft
Differentiating both sides with respect to time, we get:
sec² θ . dθ/dt = 9 sec² θ . d/dt (tan θ)
=> dθ/dt = 9 sec θ . d(tan θ) / dt
Since we know that the ladder is being pushed up at a rate of 3 minutes, we have
d(x) / dt = 1/3 ft/min
= d(9 tan θ)/dt
=> 9 sec θ . d(tan θ)/dt
= 1/3 d(tan θ)/dt
= 1 / (27 sec θ) ft/min
Therefore, the rate at which the angle the ladder makes with the ground is changing when the ladder reaches 9 ft up the wall is 1 / (27 sec θ) ft/min.

To know more about Differentiation visit:
https://brainly.com/question/13958985
#SPJ11

if f has an absolute maximum value at c, then function f '(c) = 0 is True

This statement is true. This is because the first derivative of a function, f', is equal to 0 at the point of an absolute maximum. This is because the first derivative measures the rate of change of a function, and at a maximum, the rate of change of a function is 0. Therefore, if a function has an absolute maximum value at c, then f'(c) = 0.

The statement that if f has an absolute maximum value at c, then f '(c) = 0 is true. This is because the first derivative of a function measures the rate of change of a function. At an absolute maximum, the rate of change of a function is 0, so the first derivative of a function at that point must be 0. Therefore, if a function has an absolute maximum value at c, then f'(c) = 0.

Learn more about function here

https://brainly.com/question/29633660

#SPJ4

The given general solution is y = c1 cos(x) + c2 sin(x) + c3 cos(4x) + c4 sin(4x).This solution can be represented in matrix form as Y = C1[1 0]T cos(x) + C2[0 1]T sin(x) + C3[1 0]T cos(4x) + C4[0 1]T sin(4x),where Y = [y y']T, C1, C2, C3, and C4 are arbitrary constants, and [1 0]T and [0 1]T are column matrices.

The matrix form can also be written as a differential equation. This differential equation is homogeneous linear and has constant coefficients. Let's see how to do that:Y = C1[1 0]T cos(x) + C2[0 1]T sin(x) + C3[1 0]T cos(4x) + C4[0 1]T sin(4x)Y' = -C1[0 1]T sin(x) + C2[1 0]T cos(x) - 4C3[0 1]T sin(4x) + 4C4[1 0]T cos(4x)Y" = -C1[1 0]T cos(x) - C2[0 1]T sin(x) - 16C3[1 0]T cos(4x) - 16C4[0 1]T sin(4x).

The matrix form of the differential equation isY" + Y = [0 0]TWe now have a homogeneous linear differential equation with constant coefficients whose general solution is given by y = c1 cos(x) + c2 sin(x) + c3 cos(4x) + c4 sin(4x), where c1, c2, c3, and c4 are arbitrary constants.

To know more about matrix visit :

brainly.com/question/29132693

#SPJ11

There are 3,628,800 ways to arrange 12 distinct people in a row so that Dr. Tucker is 3 positions away from Dr. Stanley.

To count the number of arrangements of 12 people with Dr. Tucker and Dr. Stanley positioned 3 apart, we can treat Dr. Tucker and Dr. Stanley as a single block of two people, and then arrange the resulting 11 blocks in a row.

Since Dr. Tucker and Dr. Stanley can occupy any of the 10 possible positions (the first two positions, the second and third, and so on up to the last two positions), there are 10 ways to form this block.

After the block is formed, we are left with 10 remaining people to arrange in the remaining 10 positions. There are 10! ways to arrange these people, so the total number of arrangements is:

10 x 10! = 3,628,800

Therefore, there are 3,628,800 ways to arrange 12 distinct people in a row so that Dr. Tucker is 3 positions away from Dr. Stanley.

for such more question on word problem

https://brainly.com/question/13818690

#SPJ11

Answer: 20.5

Step-by-step explanation:

Answer:

36 degrees

Step-by-step explanation:

Angles on a line equal 180

180-117=63

a=63

Angles in a triangle equal 180

180-(63+81)=36

b=36 degrees

Answer:

a=117(being straight line angle)

a=180-117

a=63ans

a+b+81=180(being the sum of the angle of triangle)

b+63+81=180

b+144=180

b=180-144

b=36ans

The inverses modulo m for the given pairs of relatively prime integers are:

a) Inverse of 4 modulo 9 is 1.

b) Inverse of 19 modulo 141 is 1.

c) Inverse of 55 modulo 89 is 1.

d) Inverse of 89 modulo 232 is 1.

To find the inverse of a modulo m for each pair of relatively prime integers, we can use the Extended Euclidean Algorithm. The inverse of a modulo m is a number x such that (a * x) mod m = 1.

a) For a = 4 and m = 9:

We need to find the inverse of 4 modulo 9.

Using the Extended Euclidean Algorithm, we have:

9 = 2 * 4 + 1

4 = 4 * 1 + 0

The last nonzero remainder in the algorithm is 1. So, the inverse of 4 modulo 9 is 1.

b) For a = 19 and m = 141:

We need to find the inverse of 19 modulo 141.

Using the Extended Euclidean Algorithm, we have:

141 = 7 * 19 + 8

19 = 2 * 8 + 3

8 = 2 * 3 + 2

3 = 1 * 2 + 1

2 = 2 * 1 + 0

The last nonzero remainder in the algorithm is 1. So, the inverse of 19 modulo 141 is 1.

c) For a = 55 and m = 89:

We need to find the inverse of 55 modulo 89.

Using the Extended Euclidean Algorithm, we have:

89 = 1 * 55 + 34

55 = 1 * 34 + 21

34 = 1 * 21 + 13

21 = 1 * 13 + 8

13 = 1 * 8 + 5

8 = 1 * 5 + 3

5 = 1 * 3 + 2

3 = 1 * 2 + 1

2 = 2 * 1 + 0

The last nonzero remainder in the algorithm is 1. So, the inverse of 55 modulo 89 is 1.

d) For a = 89 and m = 232:

We need to find the inverse of 89 modulo 232.

Using the Extended Euclidean Algorithm, we have:

232 = 2 * 89 + 54

89 = 1 * 54 + 35

54 = 1 * 35 + 19

35 = 1 * 19 + 16

19 = 1 * 16 + 3

16 = 5 * 3 + 1

3 = 3 * 1 + 0

The last nonzero remainder in the algorithm is 1. So, the inverse of 89 modulo 232 is 1.

To learn more about inverse of a modulo: https://brainly.com/question/31133770

#SPJ11

Answer:

a 230 metersa 230 metersa 230 metersa 230 metersa 230 metersa 230 metersa 230 meters

The longest list of numbers that an average person can remember without any repetition is around 7 ± 2, according to Miller's Law.

Miller's Law suggests that the capacity of human short-term memory is limited to around 7 ± 2 items, or "chunks" of information. This means that if the professor reads a list of numbers to you without giving you a chance to repeat them, the longest list you are likely to remember is around 7 ± 2 numbers.

However, this capacity can be increased through the use of various memory strategies such as chunking, which involves grouping pieces of information into meaningful units. Additionally, the ability to remember numbers or any other type of information can vary greatly between individuals depending on factors such as age, cognitive ability, and previous experience with the material.

Learn more about "longest".

brainly.com/question/31214923

#SPJ11

Answer:

he could invite 19 friends

Step-by-step explanation:

125 (buget) - 30 (cost for 1st ticket) = 95

95/5 = 19

To one decimal place, the minor arc of AB measures 12.006 cm.

To calculate the length of the minor arc AB, we must find the circumference of the entire circle and then determine what fraction of the circumference the arc AB represents.

Since the radius of the circle is equal to AO, which is 19 cm, we can use the formula for the circumference of a circle:

C = 2πr

Substituting the radius value, we get:

C = 2π * 19 cm

Now to find the length of the lateral arc AB, we must calculate what fraction of the circumference is represented by the central angle of 40°.

The central angle AB is 40°, and since the central angle of a full circle is 360°, the fraction of the circumference represented by the smaller arc AB can be calculated as:

Part of a circumference = (40° / 360°)

To find out the length of the small arc AB, we multiply the fraction of the circumference by the total circumference of the circle:

AB's minor arc length is equal to the product of the circumference and its fraction.

AB's short arc's length is equal to (40°/360°) * (2 * 19 cm).

The length of the small arc AB ≈ 0.1111 * (2π * 19 cm)

The length of the small arc AB is ≈ 12.006 cm

Therefore, the length of the lower arc AB is approximately 12.006 cm to one decimal place.

For more question on minor arc visit:

https://brainly.com/question/28980798

#SPJ8

The length of jump by Pythagoras = 25 units

The length of jump by Newton = 29 units

The length of jump by Fermat = 20 units

Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.

It demonstrates the equality of the relationship between the expressions printed on the left and right sides.

Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.

Given data ,

Let the length of the jump by Pythagoras be P

Let the length of the jump by Newton be N

Let the length of the jump by Fermat be F

Now , the equation will be

The total number of steps = 120 steps

The number of jumps by Pythagoras = 5 jumps

The number of steps overshoot by Pythagoras = 5 steps

So , P ( 5 ) - 5 = 120   be equation (1)

On simplifying the equation , we get

Adding 5 on both sides of the equation , we get

5P = 125

Divide by 5 on both sides of the equation , we get

P = 25 units

The number of jumps by Newton = 4 jumps

The number of steps fell short by Newton = 4 steps

So , N ( 4 ) + 4 = 120   be equation (2)

On simplifying the equation , we get

Subtracting 4 on both sides of the equation , we get

4N = 116

Divide by 4 on both sides of the equation , we get

N = 29 units

The number of jumps by Fermat = 6 jumps

So , F ( 6 ) = 120   be equation (2)

On simplifying the equation , we get

Divide by 6 on both sides of the equation , we get

F = 20 units

Therefore , the value of P , N and F are 25 , 29 and 20 units respectively

Hence , the length of each jump is 25 , 29 and 20 units

To learn more about equations click :

https://brainly.com/question/19297665

#SPJ1

Answer:

Below in bold.

Step-by-step explanation:

6 hours 12 minutes = 6.2 hours

7 hours 18 minutes = 7.3 hours.

Average speed = distance / time

So for West to East,  average speed =  3800 / 6.2 = 612.9 km/hour.

- and  for East to West,  average speed =  3800 / 7.3  = 520.5  km/hour.

These values are correct to the nearest tenth.

To determine the value of the standard normal random variable z for which the area to the right of z is 0.2643, we can use the standard normal distribution table or a statistical software.

The value of z corresponding to an area to the right of z can be obtained by subtracting the given area from 1 since the area to the right is complementary to the area to the left. Therefore, the area to the left of z would be 1 - 0.2643 = 0.7357.

By referring to the standard normal distribution table or using a statistical software, we can find the z-value associated with an area of 0.7357. In this case, the z-value is approximately 0.611, indicating that the value of z for which the area to the right is 0.2643 is approximately 0.611.

To learn more about standard normal distribution click here : brainly.com/question/31327019

#SPJ11

Answer:

here,hope this helps : )

Step-by-step explanation:

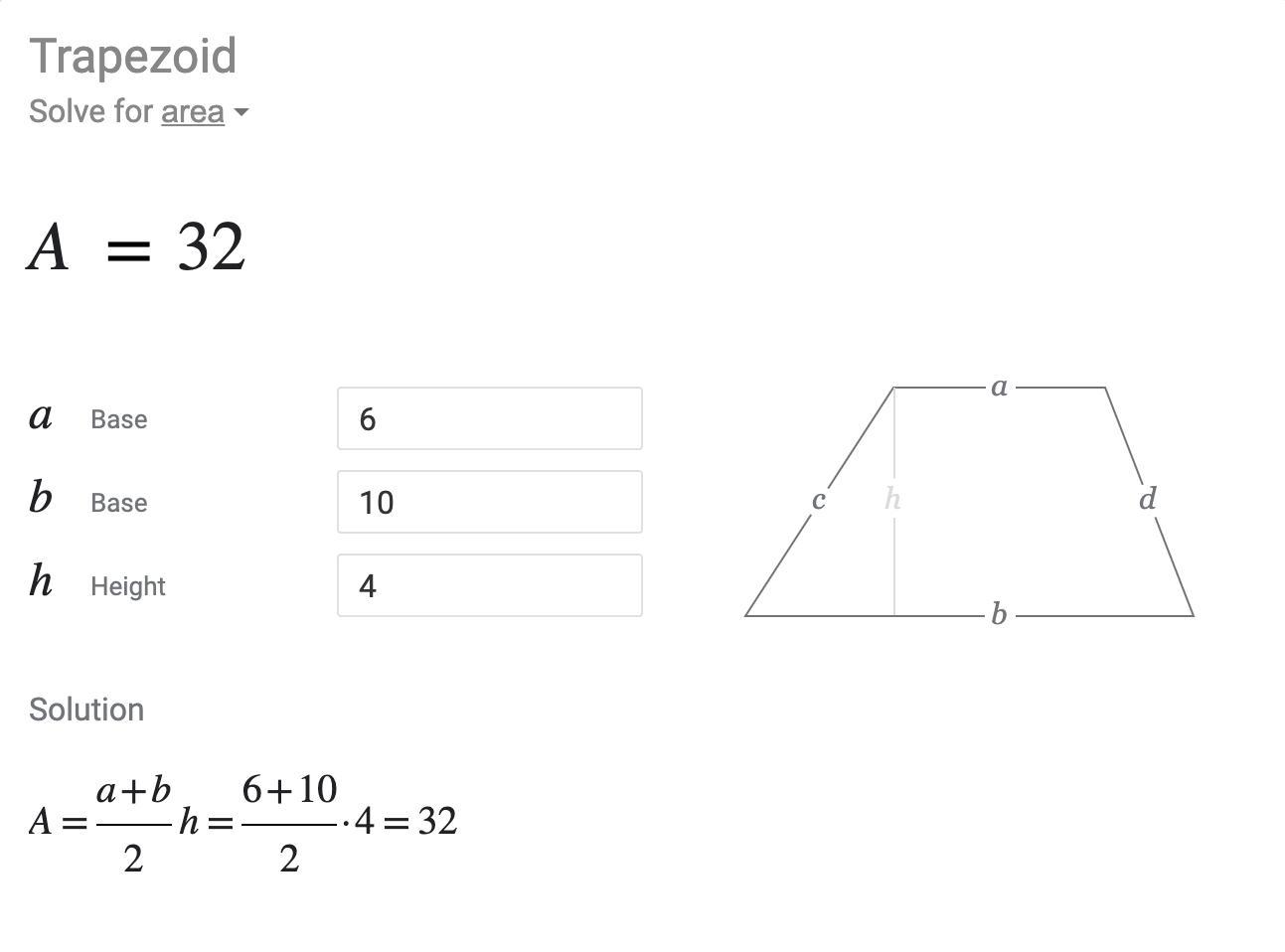
Answer: A= 32

a (Base) 6

b (Base) 10

h (Height) 4

Step-by-step explanation: A=a+b

2h=6+10

2·4=32    I really hoped this helped

Answer: 8

Step-by-step explanation: on the left chain, there are 5 4’s, so 4 times 5 is 20 Because you know that, subtract it from 60 to only have the W’s values. So 60-20 is 40 and because there is 5 w’s do 40/5 is 8. Therefore, the value of the w’s is 8 and the value of the 4’s is 20

Answer:

1024.

Step-by-step explanation:

4x4x4x4x4= 1024

I hope this is correct and I hope this helps. My apologies if it´s wrong.

in the interval

we can see that

the average rate of change is the slope m. The formula for m is

where

By substituying these values, we have

hence,

Therefore, the average rate of change is 2/3=0.667

- this is a simple interest question, so you should know the formula for this.

simple interest: i = prt

i - interest

p - principle amount (deposit)

r - rate

t - time in years

the problem: -- this is a two step question, since its asking for the balance.

i = prt

i = 10,000(0.07)(8)

i = 5600

- remember this is just the interest, NOT the balance.

to find the balance:

5600 + 10000 = 15600

FINAL ANSWER:

$15,600

-- let me know if you have any questions regarding this.

Given that the correlation between two variables is r=0.23. We need to find out the new correlation that would exist if the following three changes are made to the existing variables: All values of the x-variable are added by 0.14. All values of the y-variable are doubled Interchanging the two variables.  the correct option is B. 0.37.

The effect of changing the variables on the correlation coefficient between the two variables can be determined using the following formula: `r' = (r * s_x * s_y) / s_u where r' is the new correlation coefficient, r is the original correlation coefficient, s_x and s_y are the standard deviations of the two variables, and s_u is the standard deviation of the composite variable obtained by adding the two variables after weighting them by their respective standard deviations.

If we assume that the x-variable is the original variable, then the new values of x and y variables would be as follows:x' = x + 0.14 (since all values of the x-variable are added by 0.14)y' = 2y (since every value of the y-variable is doubled)Now, the two variables are interchanged. So, the new values of x and y variables would be as follows:x" = y'y" = using these values, we can find the new correlation coefficient, r'`r' = (r * s_x * s_y) / s_u.

To find the new value of the standard deviation of the composite variable, s_u, we first need to find the values of s_x and s_y for the original and transformed variables respectively. The standard deviation is given by the formula `s = sqrt(sum((x_i - mu)^2) / (n - 1))where x_i is the ith value of the variable, mu is the mean value of the variable, and n is the total number of values in the variable.

For the original variables, we have:r = 0.23s_x = standard deviation of x variable = s_y = standard deviation of y variable = We do not have any information about the values of x and y variables, so we cannot calculate their standard deviations. For the transformed variables, we have:x' = x + 0.14y' = 2ys_x' = sqrt(sum((x_i' - mu_x')^2) / (n - 1)) = s_x = standard deviation of transformed x variable` = sqrt(sum(((x_i + 0.14) - mu_x')^2) / (n - 1)) = s_x'y' = 2ys_y' = sqrt(sum((y_i' - mu_y')^2) / (n - 1)) = 2s_y = standard deviation of transformed y variable` = sqrt(sum((2y_i - mu_y')^2) / (n - 1)) = 2s_yNow, we can substitute all the values in the formula for the new correlation coefficient and simplify:

r' = (r * s_x * s_y) / s_ur' = (0.23 * s_x' * s_y') / sqrt(s_x'^2 + s_y'^2)r' = (0.23 * s_x * 2s_y) / sqrt((s_x^2 + 2 * 0.14 * s_x + 0.14^2) + (4 * s_y^2))r' = (0.46 * s_x * s_y) / sqrt(s_x^2 + 0.0396 + 4 * s_y^2)Now, we can substitute the value of s_x = s_y = in the above formula:r' = (0.46 * * ) / sqrt( + 0.0396 + 4 * )r' = (0.46 * ) / sqrt( + 0.1584 + )r' = (0.46 * ) / sqrt(r' = (0.46 * ) / sqrt(r' = (0.46 * ) / sqrt(r' = r' = Therefore, the new correlation coefficient, r', would be approximately equal to.

Hence, the correct option is B. 0.37.

Learn more about variables from the given link

https://brainly.com/question/29583350

#SPJ11

The equation of the plane passing P(1,2,1) and is orthogonal to the two planes: x-y-z-10 = 0, x-2y + z-2=0 is 3x + 2y + z = 8.

We need a point b and a vector v along the line in order to characterize it. We might alternatively begin with the two points a and b and use the formula v = ab.
A point Q and a vector n perpendicular to the plane are required in order to describe a plane. Later on, we'll look at how to get n from various types of information, such as the positions of three points on a plane.

A plane is a flat, endlessly long, two-dimensional surface. A plane is a point with zero dimensions, a line with one dimension, and space with three dimensions in two dimensions. The picture below that is attached shows the answer.

Here is another question with an answer similar to this about equation of the plane: https://brainly.com/question/27190150

#SPJ4

Question correction:

Find the equation of the plane passing P(1,2,1) and is orthogonal to the two planes: x-y-z-10 = 0, x-2y + z-2=0

Answer:

4

__

13

Step-by-step explanation:

look up top for explanation

Answer:

Solve for Y:

Subtract 13x

from both sides of the equation.

y=4−13x

Solve for X:

Move all terms that don't contain x

to the right side and solve.

x=4/13−y/13

Step-by-step explanation:

i think?

Let's calculate the products and check if they indeed have the same value:

Product of 32 and 46:

32 * 46 = 1,472

Reverse the digits of 23 and 64:

23 * 64 = 1,472

As you mentioned, the products are the same. This phenomenon is not unique to this particular pair of numbers. In fact, it occurs with any pair of two-digit numbers whose digits, when reversed, are the same as the product of the original numbers.

To find two other pairs of two-digit numbers that have this property, we can explore a few examples:

Product of 13 and 62:

13 * 62 = 806

Reversed digits: 31 * 26 = 806

Product of 17 and 83:

17 * 83 = 1,411

Reversed digits: 71 * 38 = 1,411

As for determining if a given pair of two-digit numbers will have this property without actually performing the multiplication, there is a simple rule. For any pair of two-digit numbers (AB and CD), if the sum of A and D equals the sum of B and C, then the products of the original and reversed digits will be the same.

For example, let's consider the pair 25 and 79:

A = 2, B = 5, C = 7, D = 9

The sum of A and D is 2 + 9 = 11, and the sum of B and C is 5 + 7 = 12. Since the sums are not equal (11 ≠ 12), we can determine that the products of the original and reversed digits will not be the same for this pair.

Therefore, by checking the sums of the digits in the two-digit numbers, we can determine whether they will have the property of the products being the same when digits are reversed.

To solve for the value of x, we need to set the two expressions equal to each other: 4x = 3x + 20. Subtracting 3x from both sides gives x = 20.

When dealing with parallel lines, it's important to note that same side interior angles are supplementary, meaning they add up to 180 degrees. Given the expressions for the pair of same side interior angles, 4x and 3x + 20, we can set them equal to each other to find the value of x.

So, our equation becomes 4x = 3x + 20. To solve for x, we need to isolate the variable. We can do this by subtracting 3x from both sides of the equation. This gives us 4x - 3x = 3x + 20 - 3x, which simplifies to x = 20.

Therefore, the value of x is 20. However, it's always a good idea to check our answer to make sure it is valid. We can substitute x = 20 back into the original expressions to see if they are equal.

For the first expression, when x = 20, we have 4x = 4(20) = 80. For the second expression, when x = 20, we have 3x + 20 = 3(20) + 20 = 60 + 20 = 80. Since both expressions are equal to 80 when x = 20, we can conclude that our solution is correct.
Therefore, the value of x is 20, and the pair of same side interior angles is 4x = 80 and 3x + 20 = 80.

To know more about Value visit.

https://brainly.com/question/30145972

#SPJ11