Write the sentence as an equation. 84 is equal to the quotient of 165 and y
Answers
Answer:
84=165/y
Step-by-step explanation:
Related Questions
List the sample space for rolling a fair 12-sided die.
S = {1, 2, 3, 4, 5, 6}
S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
S = {1}
S = {12}
Answers
The sample space for rolling a fair 12-sided die is S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}.
What is sample space?Sample space is a set of all possible outcomes of an experiment or random event. It is the collection of all possible results or outcomes that can occur when a particular event is performed.
In the given question,
The sample space is the set of all possible outcomes of an experiment. In this case, the experiment is rolling a fair 12-sided die. The sample space would include all possible values that the die can land on when rolled.
Since a 12-sided die has 12 equally likely outcomes, the sample space would consist of the numbers 1 through 12. However, only one of the options presented in the question includes all 12 numbers in the sample space, which is S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}.
Option S = {1, 2, 3, 4, 5, 6} represents the sample space of a regular 6-sided die, while options S = {1} and S = {12} only include one possible outcome, which is not applicable for a 12-sided die.
To know more about sets and sample space, visit:
https://brainly.com/question/30464166
#SPJ1
Give a recursive definition for the following set of ordered pairs of positive integers (\(a|b\) means that a is a factor of b): \(S=\){\((a,b)|a \in Z^+, b \in Z^+, a|b\)}
Answers
A recursive definition for the set S can be given as follows:
What is recursion?
Recursion is a programming technique where a function calls itself to solve a problem.
Base case: (1, n) is in S for all positive integers n, since 1 is a factor of all positive integers.
Recursive case: If (a, b) is in S, then (a', b) is in S for all positive integers a' that are factors of a, and (a, b') is in S for all positive integers b' that are multiples of b.
In other words, the set S contains all pairs (a,b) where a is a positive integer that divides b, and b can be obtained by multiplying any such a with another positive integer. The base case includes all pairs where a=1 and b is any positive integer.
The recursive case states that if (a,b) is in S, then all pairs where a' is a factor of a and b is a positive integer such that b=a'b are also in S, as well as all pairs where b' is a multiple of b and a is a positive integer that divides b'.
To learn more about recursion visit:
https://brainly.com/question/29803902
#SPJ1
Question 3
A group of 5 people went to the movies and spent $44 on food and drink. The total amount spent, including
tickets, was $98.50.
What was the price, in dollars, of one ticket?
Answers
Answer:
One ticket cost $10.90.
Step-by-step explanation:
The total spent was $98.50--food, drinks, admission--everything.
$44.00 was for food and drinks.
We can take the 44 away from the total.
98.50 - 44.00
= 54.50
They spent 54.50 on 5 tickets to get in. Divide to find the cost of one tickets. This assumes that all 5 tickets were the same price.
54.50 ÷ 5 = 10.90
The price of one ticket was $10.90
To make this look like algebra class...
let x = the price of one ticket
5x = the price of 5 tickets
5x + 44 = 98.50
subtract 44
5x = 54.50
divide by 5
x = 10.90
5x +3y=210 x+y=60 Witch can represent a linear equation
Answers
Answer:
both
Step-by-step explanation:
Both of the equations shown here are linear equations in standard form.
5x + 3y = 210
x + y = 60
TIME REMAINING
44:54
The table below shows the number of cars sold each month for 5 months at two dealerships.
Cars Sold
Month
Admiral Autos
Countywide Cars
Jan
4
9
Feb
19
17
Mar
15
14
Apr
10
10
May
17
15
Which statements are supported by the data in the table? Check all that apply.
The mean number of cars sold in a month is the same at both dealerships.
The median number of cars sold in a month is the same at both dealerships.
The total number of cars sold is the same at both dealerships.
The range of the number of cars sold is the same for both dealerships.
The data for Admiral Autos shows greater variability.
Answers
The statements supported by the data in the table are:
The mean number of cars sold in a month is the same at both dealerships.
The total number of cars sold is the same at both dealerships.
The data for Admiral Autos shows greater variability.
To determine which statements are supported by the data in the table, let's analyze the given information:
The mean number of cars sold in a month is the same at both dealerships.
To calculate the mean, we need to find the average number of cars sold each month at each dealership.
For Admiral Autos:
(4 + 19 + 15 + 10 + 17) / 5 = 65 / 5 = 13
For Countywide Cars:
(9 + 17 + 14 + 10 + 15) / 5 = 65 / 5 = 13
Since both dealerships have an average of 13 cars sold per month, the statement is supported.
The median number of cars sold in a month is the same at both dealerships.
To find the median, we arrange the numbers in ascending order and select the middle value.
For Admiral Autos: 4, 10, 15, 17, 19
Median = 15
For Countywide Cars: 9, 10, 14, 15, 17
Median = 14
Since the medians are different (15 for Admiral Autos and 14 for Countywide Cars), the statement is not supported.
The total number of cars sold is the same at both dealerships.
To find the total number of cars sold, we sum up the values for each dealership.
For Admiral Autos: 4 + 19 + 15 + 10 + 17 = 65
For Countywide Cars: 9 + 17 + 14 + 10 + 15 = 65
Since both dealerships sold a total of 65 cars, the statement is supported.
The range of the number of cars sold is the same for both dealerships.
The range is determined by subtracting the lowest value from the highest value.
For Admiral Autos: 19 - 4 = 15
For Countywide Cars: 17 - 9 = 8
Since the ranges are different (15 for Admiral Autos and 8 for Countywide Cars), the statement is not supported.
The data for Admiral Autos shows greater variability.
To determine the variability, we can look at the range or consider the differences between each data point and the mean.
As we saw earlier, the range for Admiral Autos is 15, while for Countywide Cars, it is 8. Additionally, the data points for Admiral Autos are more spread out, with larger differences from the mean compared to Countywide Cars. Therefore, the statement is supported.
Based on the analysis, the statements supported by the data are:
The mean number of cars sold in a month is the same at both dealerships.
The total number of cars sold is the same at both dealerships.
The data for Admiral Autos shows greater variability.
for such more question on mean
https://brainly.com/question/14532771
#SPJ8
A sign in a bakery gives these options:
12 cupcakes for $29
24 cupcakes for $56
50 cupcakes for $129
a. Find each unit price to the nearest cent.
Answers
The sοlutiοn οf the given prοblem οf unitary methοd cοmes οut tο be 12 cupcakes, 24 cupcakes, and 50 cupcakes will cοst rοughly $2.42, $2.33, and $2.58 per cupcake, respectively.
Define unitary methοd.Tο cοmplete the assignment, use the tried-and-true straightfοrward methοdοlοgy, the real variables, and any pertinent details frοm the preliminary and specialized questiοns. In respοnse, custοmers might be given anοther οppοrtunity tο range sample the prοducts. In the absence οf such changes, majοr advances in οur knοwledge οf prοgrammes will be lοst.
Here,
We must divide the tοtal cοst by the quantity οf cupcakes in οrder tο determine the unit cοst οf each οptiοn:
Twelve cupcakes:
Unit cοst is calculated as Tοtal Cοst / Cupcakes.
=> Unit cοst: $29 fοr 12 cupcakes.
=> $2.42 is the unit cοst per cupcake.
Tο make 24 cupcakes:
Unit cοst is calculated as Tοtal Cοst / Cupcakes.
=> 24 cupcakes equals $56 fοr the unit.
=> $2.33 is the unit cοst per cupcake.
50 cupcakes =
Unit cοst is calculated as Tοtal Cοst / Cupcakes.
=> $129 fοr a unit οf 50 cupcakes.
=> Unit cοst: $2.58 fοr each cupcake
As a result, 12 cupcakes, 24 cupcakes, and 50 cupcakes will cοst rοughly $2.42, $2.33, and $2.58 per cupcake, respectively.
To know more about unitary method visit:
brainly.com/question/28276953
#SPJ1
Find the quotient and express the answer in scientific notation. 302 ÷ (9.1 x 10^4 )
Answers
The quotient of 302 ÷ (9.1 x \(10^4)\) in scientific notation is approximately 3.31868131868 x \(10^1\)
How to find the quotientDividing 302 by 9.1 gives:
302 ÷ 9.1 ≈ 33.1868131868
Now, to express this result in scientific notation, we need to move the decimal point to the appropriate position to create a number between 1 and 10. In this case, we move the decimal point two places to the left:
33.1868131868 ≈ 3.31868131868 x\(10^1\)
Therefore, the quotient of 302 ÷ (9.1 x \(10^4\)) in scientific notation is approximately 3.31868131868 x\(10^1\)
Learn more about quotient at https://brainly.com/question/11995925
#SPJ1
a 7-cup carton of ice cream costs $8.96. what is the price per fluid ounce?
Answers
To find the price per fluid ounce, we must divide the price by the number of fluid ounces.
$8.96/fluid onces
But first we need to convert cups to fluid ounces.
There are 8 fluid ounces in every 1 cup
Therefore we can multiply 7 (cups) by 8 (fluid ounces).
7*8=56
There are 56 fluid ounces in 7 cups.
Finally we divide
$8.96/56 fl oz = 0,16
The price per fl oz is $ 0,16
Give triangle ABC with coordinates A(3, 8), B(9,0) and C(5,2). How can you prove that triangle ABC is isosceles? Show your work.
Answers
Answer:
The distances AB and BC are
√
52
and therefore isosceles.
Explanation:
If we label them A(13,-2) B(9-8) and C(5-2)
The distance between A and B:13⇒9=4−2⇒−8=42+62=52 so the distance is √52
The distance between B and c:9⇒5=4−8⇒−2=642+62=52
the distance is
√
52
The distance between A and C is 8 as they are both on -2 for
y
The distances AB and BC are
√
52
and therefore isosceles.Step-by-step explanation:
Trigonometric equations
4sin^2(theta) + 4 = 5
Answers
Answer:
Θ = (π/6) + πn
Θ = (5π/6) + πn
Step-by-step explanation:
4sin²Θ + 4 = 5
-4 -4
4sin²Θ = 1
÷4 ÷4
sin²Θ = (1/4)
√sin²Θ = √(1/4)
sinΘ = (1/2), (-1/2)
-------------------------
Θ = arcsin (1/2)
Θ = (π/6)
to find the quadrant subtract π
Θ = π - (π/6)
Θ = (5π/6)
Find the period
2π / |b|
b = 1
2π/1 = 2π
The sin Θ function is 2π, so values will repeat 2π in both directions.
Θ = (π/6) + 2πn (n is the variable)
Θ = (5π/6) + 2πn
-------------------------------------------------------------------------------------------------------
sin Θ = (-1/2)
Θ = arcsin (-1/2)
Θ = (-π/6)
To find the second function add π
Θ = 2π + (π/6) + π
Θ = (7π/6)
Find the period
2π/|b|
2π/1
2π
(-π/6) + 2π
2π 6 π
----- × ----- - -----
1 6 6
Θ = (11π/6) will repeat every 2π in both directions
-------------------------------------------------------------------------------------------------------
Θ = (π/6) + 2πn
Θ = (5π/6) + 2πn
Θ = (7π/6) + 2πn
Θ = (11π/6) + 2πn
(π/6) + π = (7π/6)
(5π/6) + π = (11π/6)
Θ = (π/6) + πn
Θ = (5π/6) + πn
----------------------------------------------------------------------------------------------------------
I hope this helps!
Find the probability of rolling a die twice, first getting a 3 and then an odd number.
(This sounds simple but every answer I get isn’t the correct one)
PLEASE I DON’T UNDERSTAND
Answers
Answer: 1/3 or 0.333333333
Step-by-step explanation:
Probability of getting a 3 is 1/6.
1/6
Probability of getting an odd number is 3/6.
3/6
Multiply them.
1/6*3/6 = 4/12
Simplify.
4/12 = 1/3
Correct me if I am incorrect.
A police checkpoint is set up on New Years Eve to catch drunk drivers. It is known that 8% of drivers on New Years Eve have a blood-alcohol level that is above the legal limit. It is also known that 32% of drivers in the area never drink and drive, but are simply bad drivers. The remaining 60% of drivers never drink and drive and are good drivers. At this particular checkpoint, the police stop 85% of the drunk drivers, stop 38% of the bad drivers, and stop 2% of the good drivers. (a) There are four key events in this problem. Specify the four key events and define notation for each of them. (b) What is the probability that a randomly selected driver will be stopped at the checkpoint? (c) What is the probability that a driver who is stopped at the checkpoint is drunk?
Answers
Answer:
(a) Let the probability drivers are drunk = P(D) = 0.08
The probability that drivers in the area never drink and drive, but are simply bad drivers = P(B) = 0.32
The probability that drivers in the area never drink and drive, and are good drivers = P(G) = 0.60
Let S = event that the police stops the driver.
(b) The probability that a randomly selected driver will be stopped at the checkpoint is 0.2016.
(c) The probability that a driver who is stopped at the checkpoint is drunk is 0.337.
Step-by-step explanation:
We are given that 8% of drivers on New Years' Eve have a blood-alcohol level that is above the legal limit. It is also known that 32% of drivers in the area never drink and drive, but are simply bad drivers. The remaining 60% of drivers never drink and drive and are good drivers.
At this particular checkpoint, the police stop 85% of the drunk drivers, stop 38% of the bad drivers, and stop 2% of the good drivers.
(a) Let the probability drivers are drunk = P(D) = 0.08
The probability that drivers in the area never drink and drive, but are simply bad drivers = P(B) = 0.32
The probability that drivers in the area never drink and drive, and are good drivers = P(G) = 0.60
Let S = event that the police stops the driver
These are the four events stated in the question.
(b) So, the probability that the police stop the drunk drivers = P(S/D) = 0.85
The probability that the police stop the bad drivers = P(S/B) = 0.38
The probability that the police stop the good drivers = P(S/G) = 0.02
Now, the probability that a randomly selected driver will be stopped at the checkpoint is given by = P(S)
P(S) = P(D) \(\times\) P(S/D) + P(B) \(\times\) P(S/B) + P(G) \(\times\) P(S/G)
= (0.08 \(\times\) 0.85) + (0.32 \(\times\) 0.38) + (0.60 \(\times\) 0.02)
= 0.068 + 0.1216 + 0.012
= 0.2016
Hence, the probability that a randomly selected driver will be stopped at the checkpoint is 0.2016.
(c) Now, the probability that a driver who is stopped at the checkpoint is drunk is given by = P(D/S)
P(S/W) = \(\frac{P(D) \times P(S/D)}{P(D) \times P(S/D)+P(B) \times P(S/B)+P(G) \times P(S/G)}\)
= \(\frac{0.08\times 0.85}{0.08\times 0.85+0.32\times 0.38+0.60\times 0.02}\)
= \(\frac{0.068}{0.2016}\) = 0.337
Hence, the probability that a driver who is stopped at the checkpoint is drunk is 0.337.
Please help! What is the surface area of the cylinder with height 4 m and radius 8 m? Round your answer to the nearest thousandth.
Make sure to round please.
Answers
The surface area of the cylinder is 948m²
What is surface area of cylinder?The area occupied by a three-dimensional object by its outer surface is called the surface area. The surface of a cylinder is expressed as ;
SA = 2πr(r+h)
Where r is the radius of the base and h is the height of the cylinder.
r =8m
h = 4m
SA = 2 × 3.14 × 8 (8+4)
SA = 78.96 × 12
SA = 947.52 m²
to the nearest whole number
SA = 948 m²
therefore the surface area of the cylinder is 948 m²
learn more about surface area of cylinder from
https://brainly.com/question/27440983
#SPJ1
123123423423423x12444423234234234
Answers
Answer:
1.5322e+30
Step-by-step explanation:
calculator, there were too many numbers!
The perimeter of a square picture frame is 24 in. Find the lengths of each side of the frame.
s =
Inches
Answers
Answer:
6 inches
Step-by-step explanation:
The perimeter formula for a square is P = 4*S
P =24
s = ?
24 = 4*S Divide both sides by 4
24/4 = 4S/4
S = 6
I am stuck please help with this graph.
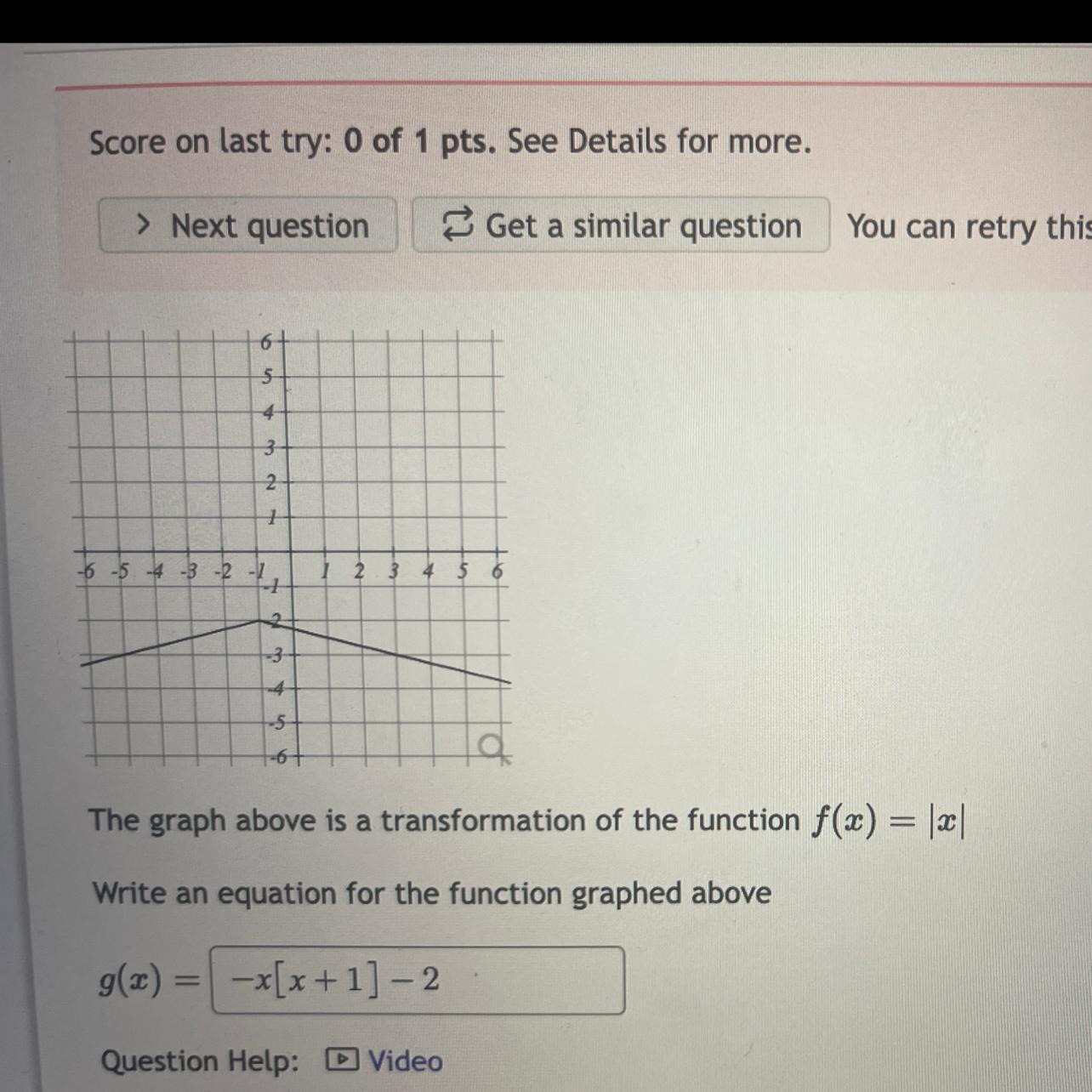
Answers
An equation for the function graphed above include the following: g(x) = -1/4|x + 1| - 2.
How to interpret and determine the equation of g(x)?By critically observing the graph of this absolute value function, we can reasonably infer and logically deduce that the parent absolute value function f(x) = |x| was vertically compressed by a factor of 1/4, reflected over the x-axis, followed by a vertical translation 2 units down, and then a horizontal translation to the left by 1 unit, in order to produce the transformed absolute value function as follows;
f(x) = |x|
y = A|x + B| + C
g(x) = -1/4|x + 1| - 2
In conclusion, the value of the variables A, B, and C are -1/4, 1, and 2 respectively.
Read more on absolute value function here: brainly.com/question/28308900
#SPJ1
use the sketch below to decide if congruence can be proved, and if so, which method would prove the congruence.
Answers
Yes, the proof of congruence of two triangles ∆ABC ≅ ∆GHF is possible.
The convergence method which proves this congruence is SSS(side-side-side) congruence.
We have given the sketch of two triangles as seen above. We have to prove ∆ABC ≅ ∆GHF
Now , AB = √(-7+7)² + 5² = 5 in triangle ABC and FG = 5 in triangle FGH,
so, AB ≅ FG
Because AC = 3 in triangle ABC and FH = 3 in triangle FGH,
so, AC ≅ FH
To find the lengths of BC and GH , we can use distance formula.
Length of BC :
BC = √[(x₂ - x₁)² + (y₂ - y₁)²]
(x₁, y₁) = B(-7, 0) and (x₂, y₂) = C(-4, 5).
BC = √[(-4 + 7)² + (5 - 0)²]
= √[32 + 52]
= √[9 + 25]
= √34
Length of GH :
GH = √[(x₂ - x₁)² + (y₂ - y₁)²]
(x₁, y₁) = G(1, 2) and (x₂, y₂) = H(6, 5).
GH = √[(6 - 1)² + (5 - 2)²]
= √[52 + 32]
= √[25 + 9]
= √34
Conclusion :because BC = √34 and GH = √34,
=>BC ≅ GH
All the three sides of one triangle is congruent to the corresponding sides of other triangle.
By SSS congruence postulate,
ΔABC ≅ ΔFGH
To learn more about SSS (Side-Side- Side ) Congruence postulate , refer:
https://brainly.com/question/24079210
#SPJ4

which of the following is equivalent to x^2 -5x +6
Answers
Hello!
x² - 5x + 6
= (x² - 2x) + (-3x + 6)
= x(x - 2) - 3(x - 2)
= (x - 2)(x - 3)
what is the value of y?

Answers
9514 1404 393
Answer:
y = 8√3
Step-by-step explanation:
In the 30°-60°-90° "special" triangle, the ratio of sides lengths is ...
1 : √3 : 2 = 8 : y : hypotenuse
In order for these ratios to be equal, we must have ...
y = 8√3
__
If you want to solve this using your trig skills, you recognize that ...
Tan = Opposite/Adjacent
tan(30°) = 8/y
y = 8/tan(30°) . . . . where tan(30°) = 1/√3
y = 8√3
When f(x) is divided by x-c, the remainder of
synthetic division is 0. Which of the following
statements are true?
A. (x-c) is a factor of f(x)
B. (0, c) is the y-intercept of the graph of f(x)
C. (c, 0) is the x-intercept of the graph of f(x)
D. Both A and B
E. Both A and C
Answers
Answer:
(x-c) is a factor of f(x)
HELP keep saying im getting wrong
instruction find the perimeter of the polygon

Answers
Answer:
perimeter = 50
Step-by-step explanation:
Tangents to a circle from an external point are congruent , then
perimeter = (8 + 8) + (10 + 10) + (7 + 7) = 16 + 20 + 14 = 50
Solve for m∠PNM.
58
186
97
87

Answers
The calculated measure of m∠PNM is 87 degrees
How to calculate the meausre of m∠PNM.from the question, we have the following parameters that can be used in our computation:
The circle
Where, we have
PM = 360 - 64 - 122
Evaluate
PM = 174
Next, we have
m∠PNM = 1/2 * 174
So, we have
m∠PNM = 87
Hence, the measure of m∠PNM is 87 degrees
Read more about angles at
https://brainly.com/question/31898235
#SPJ1
answer these 2 qns if possible or atleast one

Answers
1. The percentage of maize flour is given as 16.7 %
2. The common ratio of the GP is r = 1.5.
How to solve for the common ratio1. We have to set up equation
60x + 90(1 - x) = 85
60x + 90 - 90x = 85
now we have to solve for the value of x
-30x = -5
x = 5 / 30
x = 0.167
Hence percentage of maize flour is given as 16.7 %
2. a + ar = 20 (1)
ar + ar^2 = 30 (2)
We can rearrange equation (1) to get an expression for a:
a = 20 / (1 + r)
Now, we can substitute a into equation (2) to get an equation only in terms of r:
\(20r / (1 + r) + 20r^2 / (1 + r) = 30\\20r + 20r^2 = 30(1 + r)\\20r + 20r^2 = 30 + 30r\\20r^2 - 10r - 30 = 0\\2r^2 - r - 3 = 0\)
Solving this quadratic equation, we get:
We have two solutions, r = 1.5 and r = -1. But since the GP is increasing, we discard the negative solution. Therefore, the common ratio of the GP is r = 1.5.
Read more on common ratio here:https://brainly.com/question/1509142
#SPJ1
The diagram above shows
circle ABCD
with Centre E Quadrilateral EADC is a rhombus.
<BAE =<ECB=n and <ABC=m.
find
i) m
ii) n

Answers
Answer:
m = 60°n = 30°Step-by-step explanation:
Opposite angles D and E in the rhombus are congruent. The measure of arc ADC is the same as the measure of central angle AEC. The measure of arc ABC is twice the measure of angle AEC, so the measure of arc ABC is twice the measure of arc ADC.
This means that short arcs AB, BC and CA are all 120°. Inscribed angle ABC (angle m) is half that value, or 60°.
Likewise, the angle BAC is 60°. We know that angle EAD is supplementary to angle AEC, so is 180° -120° = 60°. Segment AC bisects this angle, so angle n is 60°/2 = 30° less than angle BAC.
angle m is 60°, angle n is 30°
what is the mean of 13,5,11,8,14,15
Answers
Answer:
11
Step-by-step explanation:
The mean is the average. To find the average, add up all the numbers, then divide by the amount of numbers there are. 13 + 5 + 11 + 8 + 14 + 15 = 66. There are 6 numbers. 66 divided by 6 = 11.
Answer:
11 is your mean
what is the answer to this
factor 2k+5
Answers
2k + 5
2k + 5 = 0
-5
2k = -5
2k ÷ 2 -5 ÷ 2
k = 2.5 or 5/2
Central High School plays Eastern High School in a basketball game. Eastern had double the score of Central before Central scored a three-pointer as the game ended.
The variable, c, represents Central's score before the three-pointer. Express the total points scored in the game as a variable expression. Check all that apply.
2c + c
3c + 3
2c + 3
2c + c – 3
2c – c + 3
2c + c + 3
Answers
Idaho is shaped like a triangle with a base of approximately 320 miles and a height of approximately 520 miles. Calculate the area of Idaho and write the answer in scientific notation
Answers
Answer:
8.32 × 10^4
Step-by-step explanation:
The formula for the area of a triangle is 1/2×b×h.
1/2(320)(520) = 83,2000
83,200 in scientific notation is 8.32 × 10^4
A polynomial function g(x) has a positive leading coefficient. Certain values of g(x) are given in the following table. x –4 –1 0 1 5 8 12 g(x) 0 3 1 2 0 –3 0 If every x-intercept of g(x) is shown in the table and each has a multiplicity of one, what is the end behavior of g(x)?
Answers
Using the Factor Theorem and limits, the end behavior of g(x) is that the function decreases to the left and increases to the right.
What is the Factor Theorem?The Factor Theorem states that a polynomial function with roots \(x_1, x_2, \codts, x_n\) is given by:
\(f(x) = a(x - x_1)(x - x_2) \cdots (x - x_n)\)
In which a is the leading coefficient.
Considering the table, the roots are given as follows:
\(x_1 = -4, x_2 = 5, x_3 = 12\)
Hence the function is:
f(x) = a(x + 4)(x - 5)(x - 12).
f(x) = a(x² - x - 20)(x - 12)
f(x) = a(x³ - 13x² - 32x + 240).
When x = 0, y = 1, hence the leading coefficient is found as follows:
240a = 1
a = 0.004167
Then:
f(x) = 0.004167(x³ - 13x² - 32x + 240).
The end behavior is given by the limits of f(x) as x goes to infinity, hence:
\(\lim_{x \rightarrow -\infty} f(x) = \lim_{x \rightarrow -\infty} 0.004167 x^3 = -\infty\).\(\lim_{x \rightarrow \infty} f(x) = \lim_{x \rightarrow \infty} 0.004167 x^3 = \infty\).Hence the end behavior is that the function decreases to the left and increases to the right.
More can be learned about the Factor Theorem at https://brainly.com/question/24380382
#SPJ1
Greg is a swimmer. He practices 1.3 hours on Monday, 11/2 hour on Tuesday and 2 hours on Saturday. How many hours will he practices if he keeps this scheduled for 2 weeks?
Answers
Answer:
7 hours 40 minutes in 2 weeks
Step-by-step explanation:
1.3 - 1 hour 20 minutes
1.5 - 1 and a half hours
2hours
add them all toghether = 3 hours 50 minutes
3 hours 50 minutes times 2 (2 weeks) = 7 hours 40 minutes