y/3 − 5 = 3 sole for y
Answers
Answer:
Step-by-step explanation:
y/3-5=3
add 5 to both sides
y/3=8
multiply both sides by 3
y=8 x 3
y=24
First Add 5 to both sides.
y/3 =3+5
Then simplify 3+5 to 8
Multiply both sides by 3
Simplify 8X3to 24 to get your anwser
Related Questions
the area of rectangle is 297 sq cm if its length is increased by 3 cm and width decreases by 1 cm its area increased by 3 cm. sq. find the length and width of rectangle
Answers
The length and width of the rectangle are 12.5 cm and 22 cm, respectively.
Let L be the length of the rectangle, and W be the width of the rectangle, then we have that:
L x W = 297 sq cm 1.
If the length is increased by 3 cm and width decreased by 1 cm, then we have that:
(L + 3) x (W - 1) = 297 + 3 sq cm -......(2).
Expand equation 2, we have:
LW + 2L - W = 300 sq cm-.......(3)
We have two equations from 1 and 3:
LW = 297 sq cm LW + 2L - W = 300 sq cm 3.
Substitute equation 1 into equation 3.
297 + 2L - W = 300 sq cm
2L - W = 3 sq cm
2L - W = 3 sq cm
2L = W + 3 sq cm
L = (W + 3)/2 sq cm
W x (W + 3)/2 = 297 sq cm
W² + 3W - 594 = 0 (W + 27) (W - 22) = 0
Therefore, the width of the rectangle is either 22 cm or -27 cm. Since the width cannot be negative, we discard the value of -27 cm. Therefore, the width of the rectangle is 22 cm. Finally, let's calculate the length of the rectangle:
L = (W + 3)/2 sq cm L = (22 + 3)/2 sq cm L = 25/2 sq cm L = 12.5 sq cm
Therefore, the length and width of the rectangle are 12.5 cm and 22 cm, respectively.
To learn more about length and width of rectangle refer :
https://brainly.com/question/12298654
#SPJ11
is the standard deviation of the numbers x, y, and z equal to the standard deviation of 10, 15, and 20 ?
Answers
This matches the placement of 10, 15, and 20 and hence the standard deviation will be the same in the two cases.
What is the standard deviation?
The standard deviation in statistics is a measure of the amount of variation or dispersion in a set of values. A low standard deviation indicates that the values are close to the set's mean, whereas a high standard deviation indicates that the values are spread out over a wider range.
Standard deviation determines how far numbers deviate from the mean. The Standard deviation of the two sets will be the same if the numbers from the respective means are placed in the same order.
This is what 10, 15, and 20 will be on a number line
10_ _ _ _15 _ _ _ _20
(15 is the mean and 10 and 20 are 5 steps away from the mean)
i) Z - X = 10
This is what Z and X will be on the number line
X _ _ _ _ _ Z
ii) Z - Y = 5
This is what Z and Y will on the number line.
Y_ _ _ _ _ Z
Together, their relative placement on the number line:
X _ _ _ _ _ Y _ _ _ _ _ Z
This matches the placement of 10, 15, and 20 and hence the standard deviation will be the same in the two cases.
To learn more about the area of the standard deviation visit,
https://brainly.com/question/475676
#SPJ1
14x-34
I need help fast!

Answers
Answer:
15.3
Step-by-step explanation:
im not 100 percent sure if this is correct but i used a calculator so...
Find p(-2) if p(x)=3x^3 -x^2 +2x-5. What does this tell you about the factors of p(x)
Answers
Answer:
\(\boxed{\textsf{ The value of the polynomial at p = (-2) is \textbf{ -37}.}}\)
Step-by-step explanation:
A polynomial is given to us and we need to find its value at p = (-2) . The given polynomial is :-
\(\sf\implies p(x)= 3x^3 -x^2 +2x-5\)
Also second part of the question says what does this tell about the factors of p(x) .
On putting p = (-2) :-
\(\sf \implies p(x)= 3x^3 -x^2 +2x-5 \\\\\sf\implies p(-2) = 3 (-2)^3-(-2)^2+2(-2)-5 \\\\\sf\implies p(-2)= 3\times (-8) -4 -4 -5 \\\\\sf\implies p(-2)=-24-4-4-5 \\\\\implies \boxed{ \pink{\sf p(-2)= (-37) }}\)
Now this tells us that ( x + 2 ) is not a factor of the given polynomial. When we divide the given polynomial by (x + 2) then the remainder will be -37 .
how to find unbiased estimator of pdf
Answers
To find an unbiased estimator of the probability density function (pdf), one must first determine the expected value of the estimator.
An estimator is unbiased if its expected value is equal to the true value of the parameter being estimated.
Let f(x|θ) be the pdf of a random variable X, where θ is a parameter of the distribution. To estimate the pdf, one can use a kernel density estimator (KDE), which is a non-parametric method that estimates the pdf using a kernel function. Let ƒ(x) be the estimated pdf using the KDE.
To find an unbiased estimator of the pdf, we need to calculate the expected value of ƒ(x) and set it equal to f(x|θ). This can be done by integrating ƒ(x) over the entire range of X:
∫ ƒ(x) dx = ∫ K((x - Xi)/h) dx
where K is the kernel function, Xi is the ith observation, and h is the bandwidth parameter.
To make this estimator unbiased, we can multiply it by a constant that ensures that its expected value equals the true pdf. This constant is typically chosen to be the reciprocal of the integral of the kernel function over the entire range of X:
ƒ^(x) = (1/nh) ∑ K((x - Xi)/h) / ∫ K(u) du
where n is the sample size.
This estimator is unbiased because its expected value is equal to the true pdf. However, it may not be the most efficient estimator in terms of mean squared error or other criteria.
To learn more about unbiased estimator click on,
https://brainly.com/question/14368422
#SPJ4
The position vector of a particle is r(t). Find the requested vector. The velocity at t=0 for r(t)=cos(4t)i+10ln(t−5)j− (t^3/6)k v(0)=2j v(0)=4i−2j v(0)=−4i−2j v(0)=−2j
Answers
The velocity vector at t = 0 is v(0) = -4i - 2j.
To find the velocity vector at t = 0 for the position vector r(t) = cos(4t)i + 10ln(t - 5)j - (t^3/6)k, we need to differentiate the position vector with respect to time.
Taking the derivative of each component of the position vector, we get:
r'(t) = -4sin(4t)i + (10/(t-5))j - (t^2/2)k
Now, we can substitute t = 0 into the derivative to find the velocity vector at t = 0:
r'(0) = -4sin(0)i + (10/(0-5))j - (0^2/2)k
= -4i + (-2)j + 0k
= -4i - 2j
Therefore, The velocity vector at t = 0 is v(0) = -4i - 2j.
Learn more about velocity here:
https://brainly.com/question/80295
#SPj11
Find all values of m so that the function
y = x^m
is a solution of the given differential equation. (Enter your answers as a comma-separated list.)
x^2y'' − 8xy' + 20y = 0
Answers
The solutions are m = 4 and m = 5. Thus, the values of m that make y = x^m a solution of the given differential equation are m = 4 and m = 5.
To find all values of m for which the function y = x^m is a solution of the given differential equation x^2y'' - 8xy' + 20y = 0, we can substitute y = x^m into the differential equation and determine the values of m that satisfy the equation.
In the first paragraph, we summarize the task: we need to find the values of m that make the function y = x^m a solution to the differential equation x^2y'' - 8xy' + 20y = 0. In the second paragraph, we explain how to proceed with the solution.
Substituting y = x^m into the differential equation, we have x^2(m(m-1)x^(m-2)) - 8x(mx^(m-1)) + 20x^m = 0. Simplifying this equation, we get m(m-1)x^m - 8mx^m + 20x^m = 0. We can factor out x^m from this equation, yielding x^m(m(m-1) - 8m + 20) = 0.
For the function y = x^m to be a solution, the expression in parentheses must equal zero, since x^m is nonzero for x ≠ 0. Thus, we need to solve the quadratic equation m(m-1) - 8m + 20 = 0. Simplifying further, we get m^2 - 9m + 20 = 0.
Factoring this quadratic equation, we have (m-4)(m-5) = 0. Therefore, the solutions are m = 4 and m = 5. Thus, the values of m that make y = x^m a solution of the given differential equation are m = 4 and m = 5.
Learn more about differential equation here:
https://brainly.com/question/25731911
#SPJ11
For the following three vectors, what is 3⋅
C
⋅(2
A
×
B
) ?
A
=3.00
i
^
+3.00
j
^
−3.00
k
^
B
=−3.00
i
^
+3.00
j
^
+4.00
k
^
C
=7.00
i
^
−7.00
j
^
Number Units
Answers
The value of 3⋅C⋅(2A×B) is 126.00. This is obtained by calculating the cross product of A and B, then taking the dot product with C and multiplying by 3.
To find the value of the expression 3⋅C⋅(2A×B), we need to calculate the cross product of vectors A and B, and then perform the dot product with vector C. Let's break it down step by step.
Vector A = 3.00i^ + 3.00j^ - 3.00k^
Vector B = -3.00i^ + 3.00j^ + 4.00k^
Vector C = 7.00i^ - 7.00j^
Step 1: Calculate the cross product of A and B.
A × B = (3.00i^ + 3.00j^ - 3.00k^) × (-3.00i^ + 3.00j^ + 4.00k^)
The cross product of two vectors can be calculated using the following formula:
A × B = (AyBz - AzBy)i^ + (AzBx - AxBz)j^ + (AxBy - AyBx)k^
Using the given vectors A and B:
A × B = (3.00 * 4.00)i^ + (-3.00 * -3.00)j^ + (3.00 * -3.00 - 3.00 * 3.00)k^
= 12.00i^ + 9.00j^ - 18.00k^
So, A × B = 12.00i^ + 9.00j^ - 18.00k^
Step 2: Perform the dot product of C and (2A×B).
C ⋅ (2A×B) = (7.00i^ - 7.00j^) ⋅ (2(12.00i^ + 9.00j^ - 18.00k^))
The dot product of two vectors can be calculated by multiplying corresponding components and summing them up:
C ⋅ (2A×B) = 7.00 * 2 * 12.00 + (-7.00) * 2 * 9.00 + 0
= 168.00 - 126.00 + 0
= 42.00
Therefore, 3⋅C⋅(2A×B) = 3 * 42.00 = 126.00.
The value of 3⋅C⋅(2A×B) is 126.00.
To learn more about vectors click here brainly.com/question/30958460
#SPJ11
After drinking, the body eliminates 37% of the alcohol present in the body per hour.
a) The amount of alcohol in grams in the body on an hourly basis is described by a discrete time dynamical system (DTDS) of the form xn+1=f(xn), where xn is the number of grams of alcohol in the body after n hours. Give the updating function f (as a function of the variable x).
b) Peter had three alcoholic drinks that brought the alcohol content in his body to 41 grams, and then he stopped drinking. Give the initial condition (in grams) for the DTDS in (a).
c) Find the solution of the DTDS in (a) with the initial condition given in (b). (Your answer will be a function of the variable n, which represents time in hours.)
Answers
The solution of the DTDS is xn = (0.63)^n * 41 grams, where n represents time in hours.
a) The updating function f(x) for the discrete time dynamical system (DTDS) can be derived from the given information that the body eliminates 37% of the alcohol present in the body per hour.
Since 37% of the alcohol is eliminated, the amount remaining after one hour can be calculated by subtracting 37% of the current amount from the current amount. This can be expressed as:
f(x) = x - 0.37x
Simplifying the equation:
f(x) = 0.63x
b) The initial condition for the DTDS is given as Peter having 41 grams of alcohol in his body after consuming three alcoholic drinks. Therefore, the initial condition is:
x0 = 41 grams
c) To find the solution of the DTDS with the given initial condition, we can use the updating function f(x) and iterate it over time.
For n hours, the solution is given by:
xn = f^n(x0)
Applying the updating function f(x) repeatedly for n times:
xn = f(f(f(...f(x0))))
In this case, since the function f(x) is f(x) = 0.63x, the solution can be written as:
xn = (0.63)^n * x0
Substituting the initial condition x0 = 41 grams, the solution becomes:
xn = (0.63)^n * 41 grams
Learn more about function at: brainly.com/question/30721594
#SPJ11
S.P=Rs 132, profit percent=10%, find C.P
Answers
Answer:
Step-by-step explanation:
10/100*132
Answer:
Step-by-step explanation:
The formula of C.P is Selling Price - Profit
Here the S.P. =132
Profit = 10%
Converting 10% = 10/100*132
= 13.2
Putting values into Formula :
132-13.2 = 118.8
so, the answer is 118.8
Get answers to more such questions from:
https://brainly.com/subject/mathematics
Please help I need the answer please

Answers
Answer:
13 yards
Step-by-step explanation:
8+5=13
Answer:
13 yards
Step-by-step explanation:
8 +5=13
A scale model of a house uses a scale 14
inch = 3 feet. If the model is 4.25
inches tall, what is the actual height of the
house?
Answers
Answer:
A scale model of a house uses a scale of 14 inches = 3 feet, this means that for every 14 inches in the model, it represents 3 feet in the actual house.
If the model is 4.25 inches tall, we can use this proportion to find the actual height of the house:
4.25 inches / 14 inches = x / 3 feet
To find the actual height of the house, we can cross-multiply and then divide:
(4.25 inches * 3 feet) / 14 inches = x
x = 1.5 feet
So the actual height of the house is 1.5 feet
(A lot of points to whoever can help me out!!) I need help with this!!

Answers
The completed statements with regards to the compound interest of the amount in the account are;
If the account has a 5% interest rate and is compounded monthly, you have $101.655 million money after 2 years
If the account has a 5% interest rate compounded continuously, you would have $106.096 million money after 2 years
What is the compound interest on an amount?Compound interest is the interest calculated based on the initial amount and the accumulated interests accrued from the periods before the present.
The compound interest formula indicates that we get;
\(A = P\cdot (1 + \frac{r}{n}) ^{n\cdot t}\)
Where;
P = The principal amount invested = $92 million
r = The interest rate = 5% monthly
n = The number of times the interest is compounded per annum = 12
t = The number of years = 2 years
Therefore; \(A = 92\cdot (1 + \frac{0.05}{12}) ^{12\times 2}\approx 101.655\)
The amount in the account after 2 years is therefore about $101.655 million
The formula for the amount in the account if the principal is compounded continuously, we get;
A = \(P\cdot e^{(r\cdot t)}\)
Therefore, we get;
\(A = 96 \times e^{0.05 \times 2} \approx 106.096\)
The amount in the account after 2 years, compounded continuously therefore, is about $106.096 million
Learn more on compound interest here: https://brainly.com/question/21487182
#SPJ1
Plesssse help me with this
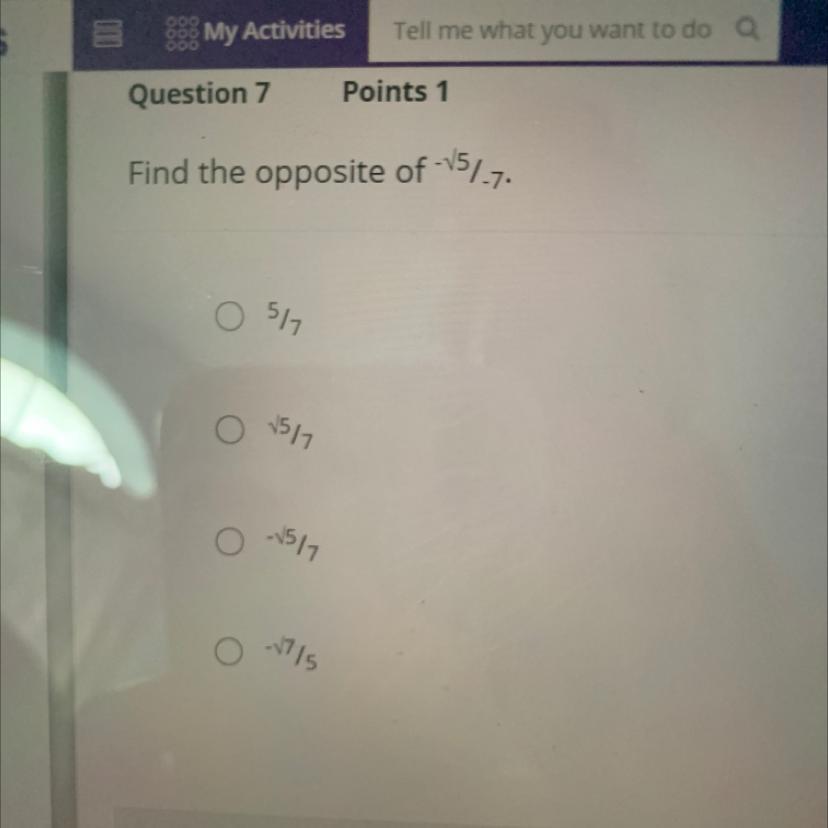
Answers
when simplified, what is the value of $\sqrt{3} \times 3^{\frac{1}{2}} 12 \div 3 \times 2 - 4^{\frac{3}{2}}$?
Answers
When simplified, the value of the expression \($\sqrt{3} \times 3^{\frac{1}{2}} 12 \div 3 \times 2 - 4^{\frac{3}{2}}$\) is 64.
Given expression is \($\sqrt{3} \times 3^{\frac{1}{2}} 12 \div 3 \times 2 - 4^{\frac{3}{2}}$\)
Simplify the exponents:
\($\sqrt{3} \times \sqrt{3} \times 12 \div 3 \times 2 - (4^{\frac{1}{2}})^3$\)
Simplify the square roots:
\($3 \times 3 \times 12 \div 3 \times 2 - 2^3$\)
Multiply and divide from left to right:
\($9 \times 12 \div 3 \times 2 - 8$\)
Perform multiplication and division:
\($108 \div 3 \times 2 - 8$\)
Evaluate the division:
\($36 \times 2 - 8$\)
72 - 8
64
Therefore, when simplified, the value of the expression is 64.
To know more about an expression follow;
brainly.com/question/19876186
#SPJ12
Gemma said, "−6 is closer to 0 than 4 because it is the smaller number."Is Gemma’s statement true or false? Give a math argument to support your answer.
Answers
Answer:
False.
Step-by-step explanation:
I believe this is a false statement, due to the fact '6' is larger than four. In this case, the six is negative. Therefore, negative numbers are always closer to zero than positive numbers.
Hope it helped :)
A dance studio has a raffle and sells 125 tickets, Kenton bought 33 of the tickets. What percent of the tickets
does Kenton have?
Answers
Answer:33/125≈26.4%
Step-by-step explanation:
End result/total=percentage
33/125=.264
Move decimal to the right two times to get percentage
=26.4%
I NEED HELP PLEASE ILL GIVE YOU BRAINLIEST T-T
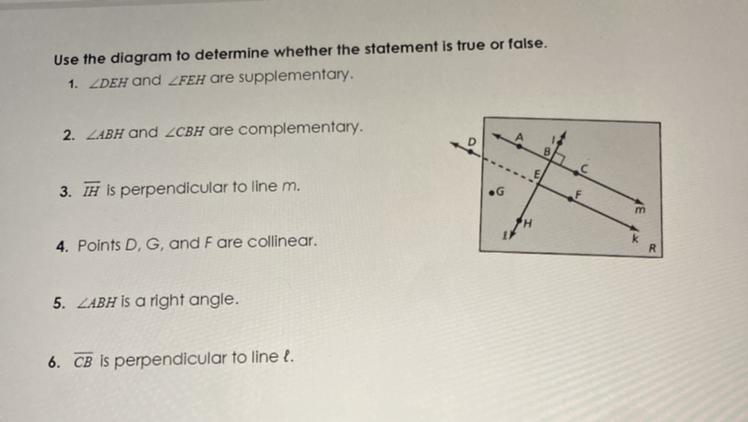
Answers
Answer:
1 true
2 false
3 true
4 false
5 true
6 true
Step-by-step explanation:
The position of a particle moving along the x axis varies in time according to the expression x=3t2, where x is in meters and t is in seconds. Evaluate its position at the following times. (a) t=3.30 s m (b) t=3.30 s+Δt xf=m (c) Evaluate the limit of Δx/Δt as Δt approaches zero to find the velocity at t=3.30 s. m/s
Answers
Given information:Position of a particle moving along the x-axis varies in time according to the expression x = 3t², where x is in meters and t is in seconds.
To determine the position at the following times. a. t = 3.30 s, b. t = 3.30 s + Δt xf and c. Evaluate the limit of Δx/Δt as Δt approaches zero to find the velocity at t = 3.30 s. a. To find the position when t = 3.30 s, substitute t = 3.30 s in x = 3t².x = 3t² = 3(3.30)² = 32.67 metersTherefore, the position at t = 3.30 s is 32.67 meters.
b. To find the position when t = 3.30 s + Δt, substitute t = 3.30 s + Δt in x = 3t².x = 3t² = 3(3.30 s + Δt)² = 3(10.89 + 6.6Δt + Δt²) = 32.67 + 19.8Δt + 3Δt²Therefore, the position when t = 3.30 s + Δt is 32.67 + 19.8Δt + 3Δt².c. Velocity is given by Δx/Δt.Δx/Δt = [x(t + Δt) - x(t)]/ΔtBy substituting the given values, we have;Δx/Δt = [x(3.30 + Δt) - x(3.30)]/Δt= [3(3.30 + Δt)² - 3(3.30)²]/Δt= 19.8 + 6ΔtTaking the limit of Δx/Δt as Δt → 0, we have;Δx/Δt = 19.8 + 6(0)Δt = 19.8Therefore, the velocity at t = 3.30 s is 19.8 m/s.
To know more about Position visit:
https://brainly.com/question/23709550
#SPJ11
can someone help me solve this question? -6 - (-10) + (-2)
Answers
Answer:
2
Step-by-step explanation:
note - (- ) = + and + (- ) = -
- 6 - (- 10) + (- 2)
= - 6 + 10 - 2
= 4 - 2
= 2
Answer:
2
Explanation:
- 6 + 10+ (- 2)
= 4+(-2)
=2
On Tuesday, the number of orange cakes Aadil needs in his sample is 5 correct to the nearest whole number. Aadil takes at random a cake from the 750 cakes made on Tuesday. b) What is the lower bound of the probability that the cake is an orange cake, giving your answer as a decimal?
Answers
Answer:
A) 210 B) 0.18
Step-by-step explanation:
got it right
cos²x-√3sinxcosx = 0
Answers
Answer:
x= п/2+пn; nE Z
x= п/6+пn; nEZ
Step-by-step explanation:
(cosx)^2- √3sinxcosx=0
Factorise it
cosx(cosx-√3sinx)=0
cosx=0 or cosx=√3sinx
x= п/2+пn; nE Z cosx/cosx= √3sinx/cosx
1/√3= tgx
x= arctg 1/√3+пn; nE Z
x= п/6+пn; nEZ
The answer is x= п/2+пn; nE Z
x= п/6+пn; nEZ
if the expression above is written in the form a bi, where a and b are real numbers, what is the value of b?
Answers
The required, expression -7 + 24i with the form a + bi, we can see that the value of b is 24.
To find the value of b in the expression (3 + 4i)^2, we can simply expand the expression and identify the coefficient of the imaginary part.
(3 + 4i)² = (3 + 4i)(3 + 4i)
Using the FOIL method, we can multiply the terms:
= 3 * 3 + 3 * 4i + 4i * 3 + 4i * 4i
= 9 + 12i + 12i + 16i²
Since i² is defined as -1, we can substitute it:
= 9 + 12i + 12i - 16
= -7 + 24i
Comparing the expression -7 + 24i with the form a + bi, we can see that the value of b is 24.
Learn more about complex numbers here:
https://brainly.com/question/32723839
#SPJ4
Complete question:
(3+4i)²
if the expression above is written in the form a+ bi, where a and b are real numbers, what is the value of b?
identify the sampling techniques used, and discuss potential sources of bias (if any). explain. assume the population of interest is the student body at a university. questioning students as they leave , a researcher asks students about their habits.
Answers
The sampling technique used in this scenario is C. Convenience sampling, because students are chosen based on the convenience of location (as they leave an academic building).
Potential sources of bias in this convenience sampling method are:
A. Because of the personal nature of the question, students may not answer honestly: When asking about eating habits, some students may feel uncomfortable or hesitant to disclose their true habits due to social desirability bias.
They might provide socially desirable responses rather than their actual habits, leading to biased or inaccurate data.
B. The sample only consists of members of the population that are easy to get: Convenience sampling relies on individuals who are readily available or accessible to the researcher.
This can result in a biased sample as it may not fully represent the diversity of the student body. For example, students who spend more time in the academic building or have certain characteristics may be overrepresented, while those who spend less time or have different habits may be underrepresented.
C. University students may not be representative of all people in their age group: The sample consists only of university students, which may not be representative of the broader population within the same age group.
University students often have distinct characteristics, lifestyles, and habits compared to individuals who are not pursuing higher education. This can limit the generalizability of the findings to the broader population.
Learn more about sampling here: https://brainly.com/question/12902833
#SPJ11
The complete question is:
Identify the sampling techniques used, and discuss potential sources of bias (if any). Explain. Assume the population of interest is the student body at a university Questioning students as they leave an academic building, a researcher asks 382 students about their eating habits What type of sampling is used? O A. Systematic sampling is used, because students are selected from a list, with a fixed interval between students on the list. O B. Cluster sampling is used, because students are divided into groups, groups are chosen at random, and every student in one of those groups is O C. Convenience sampling is used, because students are chosen due to convenience of location. sampled D. Simple random sampling is used, because students are chosen at random. E. Stratified sampling is used, because students are divided into groups, and students are chosen at random from these groups. What potential sources of bias are present, if any? Select all that apply A. □ B. C. D. Because of the personal nature of the question, students may not answer honestly. The sample only consists of members of the population that are easy to get. These members may not be representative of the population. University students may not be representative of all people in their age group. There are no potential sources of bias.
70. Machine Shop Calculations A steel plate has the
form of one fourth of a circle with a radius of 60 cen-
timeters. Two 2-centimeter holes are to be drilled in
the plate positioned as shown in the figure. Find the
coordinates of the center of each hole.
Answers
The coordinates of a point is the location of the point in a plane.
The coordinates of the centers of holes are: (48.5, 28) and (28, 48.5)
Given
\(\theta_1 = \theta_2 = \theta_3 = 30^o\)
\(R = 60\)
\(r = 56\)
I've added an attachment as an illustration
Considering \((x_1,y_1)\)
To solve for x1, we make use of cosine ratio.
So, we have:
\(\cos(\theta_1) =\frac{x}{r}\)
Make x the subject
\(x_1 = r \times \cos(\theta_1)\)
\(x_1 = 56 \times \cos(30^o)\)
\(x_1 = 48.5\)
To solve for y1, we make use of sine ratio.
So, we have:
\(\sin(\theta_1) =\frac{y_1}{r}\)
Make y the subject
\(y_1 = r \times \sin(\theta_1)\)
\(y_1 = 56 \times \sin(30^o)\)
\(y_1 = 28\)
So, we have:
\((x_1,y_1) = (48.5,28)\)
Considering \((x_2,y_2)\)
To solve for x2, we make use of cosine ratio.
So, we have:
\(\cos(\theta_1+\theta_2) =\frac{x_2}{r}\)
Make x the subject
\(x_2 = r \times \cos(\theta_1+\theta_2)\)
\(x_2 = 56 \times \cos(30+30)\)
\(x_2 = 56 \times \cos(60^o)\)
\(x_2 = 28\)
To solve for y1, we make use of sine ratio.
So, we have:
\(\sin(\theta_1+\theta_2) =\frac{y_2}{r}\)
Make y the subject
\(y_2 = r \times \sin(\theta_1+\theta_2)\)
\(y_2 = 56 \times \sin(30+30)\)
\(y_2 = 56 \times \sin(60)\)
\(y_2 = 48.5\)
So, we have:
\((x_2,y_2) = (28,48.5)\)
Hence, the coordinates of the centers of the holes are: (48.5, 28) and (28, 48.5)
Read more about coordinate geometry at:
https://brainly.com/question/8121530

if tan x = -4/3 and x is in quadrant 2, then cos2x is
Answers
Step-by-step explanation:
Trigonometric Identities are equalities that utilize trigonometry functions and hold true for all variables in the equation. The correct option is C, -7/25.
What are Trigonometric Identities?
Trigonometric Identities are equalities that utilize trigonometry functions and hold true for all variables in the equation. There are several trigonometric identities relating to the side length and angle of a triangle.
Given that the value of tan(x) = -4/3 and x is in quadrant 2.
In order to find the value of cos(2x), we can use the trigonometric identity of cos(2x), therefore, for cos(2x) we can write,
\cos(2x) = \dfrac{1-\tan^2(x)}{1+\tan^2(x)}cos(2x)=
1+tan
2
(x)
1−tan
2
(x)
Since the value of tan(x) is known, substitute the value in the identity,
\begin{gathered}\cos(2x) = \dfrac{1-(-\frac{4}{3})^2}{1+(-\frac{4}{3})^2}\\\\\cos(2x) = \dfrac{1-(\frac{16}{9})}{1+(\frac{16}{9})}\\\\\end{gathered}
cos(2x)=
1+(−
3
4
)
2
1−(−
3
4
)
2
cos(2x)=
1+(
9
16
)
1−(
9
16
)
cos(2x) = (-7/9) × (9/25)
Cancelling 9 from the numerator and the denominator,
cos(2x) = -7/25
Hence, if tanx=-4/3 and x are in quadrant 2 then cos2x=-7/25.
Learn more about Trigonometric Identities:
https://brainly.com/question/13094664
What is the domain of the function graphed below?
Pls I need it now
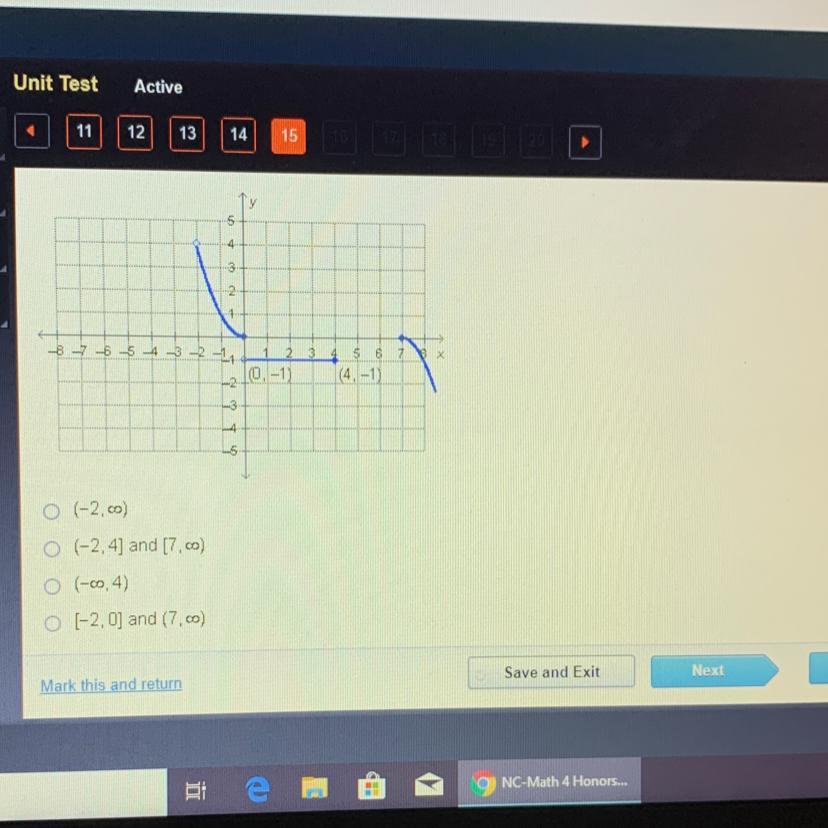
Answers
Answer:
A (-2,infinite)
Step-by-step explanation:
Based on all the fragments, the domain starts at coordinate on the first fragment (-2,4) and ends in the third fragment, where wee see the line extend to infinity along the x axis
Need to turn this in today help!!

Answers
The angle 2 is 149° , angle 3 is 31° , angle 4 is 149°
What is the name for two opposing angles?
Angles where two lines cross that are directly opposite one another are known as opposing angles. The vertex, where the lines come together to produce the angle, is the location of the junction. Vertical angles are another name for opposite angles.
Given that :
Angle 1 is = 31°
Angle 2 is = 180 - 31 = 149° (As in a line total angle is 180°)
Angle 3 is = 31° (As equal opposite angle with angle 1)
Angle 4 is = 149° (As equal opposite angle with angle 2)
Learn more about Vertical angles
https://brainly.com/question/18450499
#SPJ1
Expand the expression −11(3c−2d)
using the Distributive Property.
Answers
Answer:
-33c+22d
Step-by-step explanation:
=(−11)(3c+−2d)
=(−11)(3c)+(−11)(−2d)
The area of a rectangle is 8w + 18 square feet. The length of the rectangle is 2 feet. Use factoring to write an expression to represent the width of the rectangle.
Answers
Answer:
The expression that represents the width of the rectangle is 4w + 9
Step-by-step explanation:
The formula of the area of the rectangle is A= length x width
The area of a rectangle is 8w+18 square feet.
A= 8w+18
The HCF of 8 and 18 is 2
Divide each term of the area by 2 to get 2 as a common factor
8 /2 =4 and 18 /2 = 9
A=2(4w+9)
The length of the rectangle is 2 feet
Substitute it in the formula of the area above
A=2 x width
A=2 width
Equate the two right sides of the area
2 width =2(4w+9)
Divide both sides by 2
The width = 4w+9