Answers
Answer:
I Hope it will help u
Step-by-step explanation:
Your solution is in image ,
please brain-list it it takes effort ,
I have a channel please subscribe to it i will be thank full
" ZK SOFT&GAMING" search this on you-tube.


Related Questions
a triangle has side lengths in the ratio is inscribed in a circle with radius . what is the circumference of the triangle?
Answers
Therefore, the circumference of the triangle is 2r, which is equal to the diameter of the circle.
To find the circumference of the triangle, we need to first find the lengths of its sides. Let the three sides be x, y, and z, such that x:y:z is the given ratio. Without loss of generality, we can assume that x is the shortest side.
Let k be a constant such that y = kx and z = lx, where k and l are constants. Then, we have:
x + kx + lx = 2r
Simplifying this equation, we get:
x(1 + k + l) = 2r
So, we have:
x = (2r)/(1 + k + l)
y = kx = k(2r)/(1 + k + l)
z = lx = l(2r)/(1 + k + l)
The circumference of the triangle is the sum of its three sides:
C = x + y + z
Substituting the expressions for x, y, and z, we get:
C = (2r)/(1 + k + l) + k(2r)/(1 + k + l) + l(2r)/(1 + k + l)
Simplifying this expression, we get:
C = (2r(1 + k + l))/(1 + k + l)
C = 2r
Therefore, the circumference of the triangle is 2r, which is equal to the diameter of the circle.
learn more about circumference of the triangle
https://brainly.com/question/20593200
#SPJ11
The area of the triangle is equal to A) 8.64. The Correct option is A) 8.64.
Let the lengths of the triangle be, 3x,4x,5x
Square of largest side = \(25x^{2}\)
Sum of square of other sides = \(3x^{2} + 4x^{2} = 25x^{2}\)
It is a right-angled triangle because the square of the greatest side equals the sum of the squares of the other sides.
The circumference of a right-angled triangle has a diameter equal to its hypotenuse.
hence, 5x=6 or x= \(\frac{6}{5}\)
Now, two perpendicular sides are then, \(\frac{18 }{5} , \frac{24}{5}\)
\(Area = \frac{1}{2} \times \frac{18}{5} \times \frac{24}{5} = 8.64\)
for such more question on triangle
https://brainly.com/question/27447563
#SPJ11
Question
A triangle with side lengths in the ratio 3 : 4 : 5 is inscribed in a circle of radius 3. The area of the triangle is equal to
A. 8.64
B. 12
C. 6
D. 10.5
What is remainder when x3 2x² X 1 is divided by x 1?
Answers
When x^3+2x^2+x+1 is divided by (x+1) then remainder is 1.
In the given question, we have to find what is remainder when x^3+2x^2+x+1 is divided by (x+1).
To find the remainder there are two ways. First we divide the x^3+2x^2+x+1 by (x+1). Second we find the value of from (x+1) by equating (x+1) equal to zero. The put the value of x in the expression x^3+2x^2+x+1.
In this we ca easily find the remainder.
Now we firstly find the value of x;
(x+1) = 0
Subtract 1 on both side we get;
x= −1
Now put x= -1 in the expression x^3+2x^2+x+1.
x^3+2x^2+x+1 = (−1)^3+2(−1)^2+(−1)+1
x^3+2x^2+x+1 = −1+2−1+1
x^3+2x^2+x+1 = 1
Hence, when x^3+2x^2+x+1 is divided by (x+1) then remainder is 1.
To learn more about division of polynomial link is here
brainly.com/question/29718477
#SPJ4
The right question is:
What is remainder when x^3+2x^2+x+1 is divided by (x+1)?
Please answer<3
-2w - 5w =
Answers
Answer:
the answer is -7w
Step-by-step explanation:
-2w - 5w = -7
How would you begin to plot the ordered pair ( 6,2)?
Answers
Need help with this trigonometry word problem
A kite is flying at a height of 65 m attached to a string. If the inclination of the string with the ground is 31°, find the length of string.
Show your work please
Answers
Answer:
let KL be the string PL be perpendicular distance between them. and KL be height of kite flying.
in right angled triangle
relationship between perpendicular and hypotenuse is given by sin angle
sin 31°=p/h
h=65/sin31
KP=126.2m
the length of string is 126.2m

Answer:
127.45 m
Step-by-step explanation:
Given :-
Height of kite = 65 m .Inclination of string = 31° .To Find :-
The length of the string .Solution :-
Here we need to find out the length of the string here if we imagine a right angle triangle in which the height of the kite will be the perpendicular of the triangle and the length of the string will be the hypotenuse of triangle .
And the angle between the the string and the ground will be 31°.
Here we can use ratio of sine as ,
> sin∅ = p/h
> sin 31° = 65m/ h
> h = 65m/sin 31°
> h = 65m/0.51
> h = 127 .45 m
A two-sample t-test for a difference in means will be conducted to investigate whether the average length of a cell phone call is shorter this year compared with 5 years ago. From a random sample of 35 phone call records this year, the average length was 25 minutes with a standard deviation of 4 minutes. From a random sample of 32 phone call records from 5 years ago, the average length was 27 minutes with a standard deviation of 5 minutes. The difference (this year minus five years ago) in means will be calculated With a null hypothesis of no difference in length, which of the following is a correct test statistic for the test?
A. t = 25-27/(√4^2/35+5^2/32)
B. t = 25-27/(√4/35+5/32)
C. t = 25-27/(√4^2/35+√5^2/32)
D. t = 27-25/(√4^2/35+5^2/32)
E. t = 27-25/(√4/35+5/32)
Answers
The correct test statistic is: A. t = (25-27)/(√4²/35+5²/32)
What is test statistic?
The correct test statistic for the two-sample t-test is:
t = (x1 - x2) / √[s1²/n1 + s2²/n2]
where x1 and x2 are the sample means, s1 and s2 are the sample standard deviations, and n1 and n2 are the sample sizes.
Using the given values, we have:
x1 = 25, x2 = 27, s1 = 4, s2 = 5, n1 = 35, n2 = 32
Substituting these values into the formula, we get:
t = (25 - 27) / √[(4²/35) + (5²/32)]
Simplifying, we get:
t = -2 / √[0.4632 + 0.7813]
t ≈ -2.64
Therefore, the correct test statistic is:
A. t = (25-27)/(√4²/35+5²/32)
To know more about test statistic, visit:
https://brainly.com/question/14128303
#SPJ1
let f be the function with derivative given by f'(x) = sin(x2 − 3). at what values of x in the interval −3 < x < 3 does f have a relative maximum?A) -1.732 and 2.478 only B) -2.478 and 1.732 only C) 2.138, 0,and 2.138 D) -2.478 -1.732, 1.732, and 2.478
Answers
The interval where the derivative function f'(x) has a relative maximum is -2.478 and 1.732 (B) only.
To find the relative maximum of a function, we need to find the critical points of the derivative function. Critical points are where the derivative function is equal to zero or undefined. In this case, the derivative function is f'(x) = sin(x^2 − 3).
To find the critical points, we need to set the derivative function equal to zero and solve for x:
sin(x² − 3) = 0
x² − 3 = nπ, where n is an integer
x² = nπ + 3
x = ±√(nπ + 3)
We need to find the values of x that are in the interval −3 < x < 3. By plugging in different values of n, we can find the critical points in this interval:
n = 0: x = ±√3 ≈ ±1.732
n = 1: x = ±√(π + 3) ≈ ±2.478
n = 2: x = ±√(2π + 3) ≈ ±2.915 (not in the interval)
So the critical points in the interval are -2.478, -1.732, 1.732, and 2.478.
To determine which of these are relative maximums, we need to look at the sign of the derivative function on either side of the critical points. If the derivative function changes from positive to negative at a critical point, then that point is a relative maximum.
At x = -2.478, the derivative function changes from positive to negative, so this is a relative maximum.
At x = -1.732, the derivative function changes from negative to positive, so this is not a relative maximum.
At x = 1.732, the derivative function changes from positive to negative, so this is a relative maximum.
At x = 2.478, the derivative function changes from negative to positive, so this is not a relative maximum.
Therefore, the values of x in the interval −3 < x < 3 where f has a relative maximum are -2.478 and 1.732.
Learn more about Derivative Function here: brainly.com/question/25752367
#SPJ11
PLEASE HELP!! WORTH 20 points. AND WILL NAME BRAINLIEST. IF BLURRY JUST ZOOM IN!! IF YOUR NOT GONNA ANSWER WITH A REASONABLE ANSWER THEN DONT COMMENT.

Answers
Answer:
These methods convert everything to radians
Step-by-step explanation:
Length of arc DC fromula is radius*angle in radians
Radius of the circle of DC is 8 cm aka the outer circle.
The angle inside is 130 degrees, in radians convert and multiply by 180/\(\pi\)
givong 130 degrees to be 13/18π
using formula, arc DC is 8*13/18π
=52/9π (in terms of pi) or 18.15 cm
or 130/360*(2π8)=18.15 (not using radians)
Length of arc QT regards the inner circle of radius 4 cm. Convert 130 degrees to radians. Using same formula as above, length of arc =4*13/18π
=26/9π or 9.08 cm
or 130/360*(2π4)=9.08 (not using radians)
Area of sector DEC suspended angle is 130 degrees of 13/18π radians. regarding large outer circle radius 8 cm.
Use formula 0.5*r^2*angle in radians fro area of sector gives:
0.5*8^2*13/18π
=208/9π or 72.61 cm^2
or 130/360*(π8^2)=72.61 (not using radians)
The area of sector QET angle 13/18πv rad and radius 4 cm using same forumla as above gives
0.5*13/18π*4^2
=52/9π or 18.15cm^2
or 130/360*(π4^2)=18.15 (not using radians)
Radian measure of angle DEC is 130 degrees again convert to radians by multiplying by π/180 gives
=13/18π
Radian measure of angle QET IS ALSO 130 degrees also
=13/18π
Which expression is equivalent to (st)(6)?
s(t(6))
s(x) × t(6)
s(6) × t(6)
6 × s(x) × t(x)
Answers
Answer: The expression (st)(6) means to substitute the value of 6 into the function (st) which is the composition of two functions s and t. The order of applying the functions is crucial, so the first function s will be applied to the result of the second function t after being applied to the 6. So the correct equivalent of (st)(6) is s(t(6))
Step-by-step explanation:
Which expression is equivalent to the phrase shown below?
The quotient of the sum of 2t and 2, and twice the cube of s
A. 2t +23s2 C. 2t+23s2
B. 2t +22s3 D. 2t+22s3
Answers
Answer:
The answer is the letter D
Step-by-step explanation:
The sum of 2t and 2 could be written as:
\(a=2t+2\)
Now, the twice of the cube of s will be:
\(b=2s^{3}\)
Finally, the quotient between a and b will be:
\(\frac{a}{b}=\frac{2t+2}{2s^{3}}\)
Therefore the answer is the letter D
I hope it helps you!
Make c the subject:
A=b+cd
Answers
All you have to do is this! Please mark me as brainliest
Answer:
C = A/d - b/d or C = (A - b)/d
Step-by-step explanation:
A = b + cd
A - b = cd
A/d - b/d = c
Find and classify the critical points of f(x,y)=8r³+ y² + 6xy
Answers
The critical points of the function are (0, 0) and (3/4, -9/4), To classify the critical points, we need to examine the second partial derivatives of f(x, y) at each point
To find the critical points of the function f(x, y) = 8x^3 + y^2 + 6xy, we need to find the values of (x, y) where the partial derivatives with respect to x and y are equal to zero.
Taking the partial derivative with respect to x, we have:
∂f/∂x = 24x^2 + 6y = 0.
Taking the partial derivative with respect to y, we have:
∂f/∂y = 2y + 6x = 0.
Solving these two equations simultaneously, we get:
24x^2 + 6y = 0,
2y + 6x = 0.
From the second equation, we can solve for y in terms of x:
Y = -3x.
Substituting this into the first equation:
24x^2 + 6(-3x) = 0,
24x^2 – 18x = 0,
6x(4x – 3) = 0.
Therefore, we have two possibilities for x:
1. x = 0,
2. 4x – 3 = 0, which gives x = ¾.
Substituting these values back into y = -3x, we get the corresponding y-values:
1. x = 0 ⇒ y = 0,
2. x = ¾ ⇒ y = -9/4.
Hence, the critical points of the function are (0, 0) and (3/4, -9/4).
To classify the critical points, we need to examine the second partial derivatives of f(x, y) at each point. However, since the original function does not provide any information about the second partial derivatives, further analysis is required to classify the critical points.
Learn more about partial derivatives here:
https://brainly.com/question/32387059
#SPJ11
Milo drives 126 miles on 7.5 gallons of gas. How far does he travel on each gallon of gas?
1.68 miles
16.8 miles
168 miles
1.680 miles
Answers
Answer:
16.8
Step-by-step explanation:
126/7.5 = 16.8
Answer:
16.8 miles
Step-by-step explanation:
Set up a proportion: Then do,
1) 126(1) / 7.5(x)
2) 126 / 7.5
3) 16.8
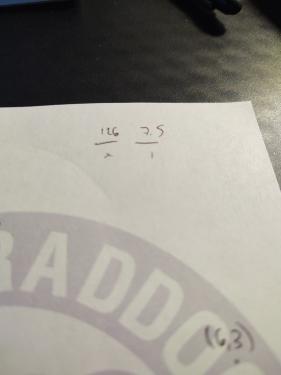
what sample size is necessary for a 90% confidence interval about the mean height of a shrub if we want a margin of error of 0.5 inches and the population standard deviation is known as 1.3 inches.
Answers
The sample size necessary for a 90% confidence interval about the mean height of a shrub with a margin of error of 0.5 inches and a population standard deviation of 1.3 inches is 18.
Margin of error is defined as the degree of the sampling errors in statistics. It can be calculated using the formula below.
MOE = z x (SD / √n)
where MOE = margin of error = 0.5 inches
z = found by using a z-score table
SD = sample standard deviation = 1.3 inches
n = sample size
At 90% confidence interval, the area in each tail of the standard normal curve is 5, and the cumulative area up to the second tail is 95.
(100 - 90) / 2 = 5
100 - 5 = 95
Find 0.95 in the z-table to get the value of z.
At p = 0.95, z = 1.647
Plug in the values to the formula and solve for the sample size, n.
MOE = z x (SD / √n)
0.5 = 1.647 x (1.3 / √n)
√n = 1.647(1.3) / 0.5
n = 18.34
n = 18
Learn more about margin of error here: brainly.com/question/10218601
#SPJ4


On January 1, 2017, the Clutz Company purchased 30% of the 1,000,000 shares of Nancy's common stock for $15,000,000 when 30% of Nancy's net assets totaled $12,000,000. The excess of purchase price over the underlying assets was attributable to undervalued depreciable plant assets with a remaining useful life of ten years. Nancy reported net income of $8,000,000 and paid cash dividends of $2,000,000 during 2017.
Refer to Exhibit 13-2. What should the income reported by Clutz during 2017 from its investment in the Nancy Company be?
a. $2,100,000
b. $2,900,000
c. $2,400,000
d. $ 600,000
Answers
The income reported by Clutz during 2017 from its investment in the Nancy Company be $2,100,000. So, the option a is correct.
Acquisition price for 30% of the Stock (A) = $15,000,000
Fair Value of Nancy's Assets, 30% (B) = $12,000,000
Undervalued depreciable assets are to blame for the excess of consideration above fair value (A-B) = $ 3,000,000
Calculation of Nancy's Investing Income for 2017
Dividends that Nancy paid out (a) = $2,000,000 × 30%
Dividends that Nancy paid out (a) = $ 600,000
Clutz's Part of Nancy's Income (b) = ($8,000,000 - $2,000,000) × 30%
Clutz's Part of Nancy's Income (b) = $6,000,000 × 30/100
Clutz's Part of Nancy's Income (b) = $1,800,000
Depreciation calculations for undervalued assets
Value of Assets = $3,000,000
Useful Life = 10 years
Depreciation for 2017 = $3,000,000/10
Depreciation for 2017 = $300,000
Depreciation of Undervalued Assets (c) = $ 300,000
Therefore Income from Investment to be reported by Clutz(a + b - c) = $600,000 + $ 1,800,000 - $ 300,000
Income from Investment to be reported by Clutz(a + b - c) = $21,00,000
So the option a is correct.
To learn more about Income from Investment link is here
brainly.com/question/29342476
#SPJ4
please, please help me with this!! it’s very important.

Answers
The parabola's vertex is located at (-2, 8). The parabola's graph is then depicted below.
Let a be the leading coefficient and the parabola's vertex be the point (h, k). The parabola's equation will therefore be stated as,
y = a(x - h)² + k
The parabola's equation is stated as,
y = -(x + 2)² + 8
The downward-pointing parabola is represented by the negative sign.
The vertex of the parabola is at (-2, 8), according to the equation above. The parabola's graph is then depicted below.
More about the equation of the parabola link is given below.
https://brainly.com/question/20333425
#SPJ1

Your class had an ant farm with 32 ants. If the number of ants increased by a factor of 5 every week, how many ants would there be after 3 weeks? Write your answer in numerical form.
Answers
Answer:
the answer is either 47 or 35
Step-by-step explanation:
this is. Because the only factors of five are 5 or 1 so all you can do is 5x3weeks=15 so 32+15=47
Or it can be 32+(1x3weeks)=32+3=35
what is 1/3 of 540 help
Answers
Answer:
180
Step-by-step explanation:
1/3 of 540 is just 540/3 which is equal to 180
Answer: 180.00
Step-by-step explanation:
One third of 540 is simply one third times 540,
One/third x 540
Furthermore, you can convert "one" to "1" and "third" to "3" and then the equation and answer is: 180.00
Which of the following sequences is an arithmetic sequence? Why?
1. 3, 7, 11, 15, 19
2. 4, 16, 64, 256
3. 48, 24, 12, 6, 3, ...
4. 1, 4, 9, 16, 25, 36
5. 1, 1/2, 0, -1/2
6. -2, 4, -8, 16, ...
7. 1, 0, -1, -2, -3
8. 1/2, 1/3, 1/4, 1/5, ...
9. 3x, x, x/3, x/9, ...
10. 9.5, 7.5, 5.5, 3.5, ..
Answers
Answer: sequences 1,5,7,9,10
Step-by-step explanation:
An arithmetic sequence is defined by a sequence of numbers with a common difference between terms. Technically if x=0 in q9 we have a constant sequence, which by definition is arithmetic. However if x does not equal 0 it is not arithmetic.
It takes a machine at a seafood company 20 s to clean 3 1 ib of shrimp _ 3
Answers
It takes a machine at a seafood company 20 seconds to clean 3 pounds of shrimp. The rate of the machine is 0.15 pound per second
What is an equation?An equation is an expression that shows the relationship between two numbers and variables.
An independent variable is a variable that does not depend on any other variable for its value whereas a dependent variable is a variable that depend on any other variable for its value.
It takes a machine at a seafood company 20 seconds to clean 3 pounds of shrimp. Hence:
Rate of the machine = 3 pounds / 20 seconds = 0.15 pound per second
It takes a machine at a seafood company 20 seconds to clean 3 pounds of shrimp. The rate of the machine is 0.15 pound per second
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1
In Problems 53-56, write a system of linear inequalities for the given graph. 54.
Answers
Once we have identified the lines, we can write inequalities that describe the region that is shaded.
To write a system of linear inequalities for a given graph, we need to identify the lines that make up the boundary of the shaded region on the graph.
These lines will be in the form of y = mx + b, where m is the slope of the line and b is the y-intercept. Once we have identified the lines, we can write inequalities that describe the region that is shaded.
For example, suppose we have a graph with a shaded region that is bounded by the lines y = -x + 3, y = x - 1, and y = 0. To write a system of linear inequalities for this graph, we would write:
y ≥ -x + 3
y ≥ x - 1
y ≤ 0
The first two inequalities describe the region above the lines y = -x + 3 and y = x - 1, and the third inequality describes the region below the x-axis. Together, these inequalities describe the shaded region on the graph.
In summary, to write a system of linear inequalities for a given graph, we need to identify the lines that make up the boundary of the shaded region, and write inequalities that describe the region that is shaded.
To know more about linear click here
brainly.com/question/30444906
#SPJ11
Solve the equation.
2= n/3 n=
Answers
Answer: n = 6
Step-by-step explanation:
First you have to isolate the n by multiplying each side by 3. Than you get n=6
Answer:
6
Step-by-step explanation:
Multiply both sides by 3:
2 times 3 = 6
n/3 times 3 = n
n = 6
Can anyone help me with this?

Answers
\(Draw\ \overline {AB}\perp\overline {CD}\ at\ point \ A.\)

between wich two intergers does √11 lie
Answers
Answer:
3 and 4
Step-by-step explanation:
a man left 1/2 of his money to his first son 3/8 to his second son, the rest 80,000 to his third son.how much did he he leave to his second son
Answers
As per the given conditions in the question, the amount of money that the second son was left with by the man is 2,40,000.
How do you add two fractions with different denominators?To add two fractions with different denominators, you must first find a common denominator. A common denominator is a number that is divisible by both denominators of the fractions. Once you have a common denominator, you can add the numerators of the fractions together and place the sum over the common denominator. Then simplify the fraction if possible.
What is the reciprocal of a fraction?The reciprocal of a fraction is another fraction whose numerator and denominator are flipped. For example, the reciprocal of the fraction 2/3 is 3/2. The product of a fraction and its reciprocal is always equal to 1. To find the reciprocal of a fraction, simply swap the numerator and denominator.
Considering the conditions given in the question,let us suppose that the third son was left with x part of the money,
so we can use the equation,
part of money left for fist son + part of money left for second son + part of money left for third son = total part of money
or, 1/2 + 3/8 + x = 1
therefore, x = 1/8
Also we know that the third son was left 80,000 ,
so 1/8 of total money = 80,000
therefore, total money = 80000 * 8 =6,40,000
Now the amount left for the second son is , 3/8 of total money
which is equal to , 3/8 of 6,40,000 = 2,40,000
To learn more about fractions visit:
https://brainly.com/question/10354322
#SPJ1
if it is assumed that all 52 5 poker hands are equally likely, what is the probability of being dealt a flush?
Answers
If it is assumed that all 52 5 poker hands are equally likely, the probability of being dealt a flush is 0.001981
Flush means all 5 cards are of the same suit.
Now, we need to select one suit out of 4 which can be done in ⁴C₁ ways.
Now, when the suit is selected, we have to select 5 cards from that specific suit. This can be done in ¹³C₅ ways
In the game of poker, there are ⁵²C₅ possible hands.
So, the probability of a flush is given by:
P = (⁴C₁ × ¹³C₅)/⁵²C₅
P = (4 × 1287)/2598960
P = 5148/2598960
P = 0.001981 or 1.981 × 10⁻³ or 0.1981 %
To know more about probability here:
brainly.com/question/11234923
#SPJ4
Which expression is undefined?

Answers
Answer:
Option D is the correct answer
Step-by-step explanation:
\( \frac{8}{( - 2 + 2)} = \frac{8}{0} = undefined \\ \)
Compute f′(a) algebraically for the given value of a. f(x)=−7x+5;a=−6
Answers
The f′(a) when a = −6 is -7. This means that the slope of the tangent line of the graph of f(x) at x = -6 is -7.
To compute f′(a) algebraically for the given value of a, we use the following differentiation rule which is known as the Power Rule.
This states that:If f(x) = xn, where n is any real number, then f′(x) = nxⁿ⁻¹This is valid for any value of x.
Therefore, we can differentiate f(x) = −7x + 5 with respect to x using the power rule as follows:
f(x) = −7x + 5
⇒ f′(x) = d/dx (−7x + 5)
⇒ f′(x) = d/dx (−7x) + d/dx(5)
⇒ f′(x) = −7(d/dx(x)) + 0
⇒ f′(x) = −7⋅1 = −7
Hence, the derivative of f(x) with respect to x is -7.Now, we evaluate f′(a) when a = −6 as follows:f′(x) = −7 evaluated at x = −6⇒ f′(−6) = −7
Therefore, f′(a) when a = −6 is -7. This means that the slope of the tangent line of the graph of f(x) at x = -6 is -7.
Learn more about Power Rule here:
https://brainly.com/question/23418174
#SPJ11
determine the set of points at which the function is continuous h(x, y) = (e^x e^y)/ (e^xy - 1)
Answers
The set of points at which the function is continuous h(x, y) = (eˣ eʸ)/ (eˣʸ - 1) when xy is not zero,or x or y is not zero.
To determine the set of points at which the function h(x, y) = (eˣ eʸ)/ (eˣʸ - 1) is continuous,
we need to look at the denominator of the expression, eˣʸ - 1. This denominator is equal to zero only when eˣʸ = 1, which means that xy = 0.
Therefore, the set of points where the function h(x, y) is not continuous is when xy = 0, or when x = 0 or y = 0.
At these points, the denominator of the expression becomes zero, and the function is not defined.
Thus, the set of points where the function h(x, y) is continuous is when xy ≠ 0, or when x ≠ 0 and y ≠ 0.
At these points, the denominator of the expression is never zero, and the function is well-defined and continuous.
Learn more about continuous function : https://brainly.com/question/18102431
#SPJ11
Each side of the tree house is the same length. Peter plans on putting a pentagonal roof on the tree house. The sides of the roof will be 6 inches longer than the sides of the tree house. A large pentagon is labeled n 6. A smaller pentagon inside of the large one is labeled n. A solid circle is in the middle of the small pentagon. Which expression represents the perimeter of the roof, in inches? 35n n 30 5n 6 5n 30.
Answers
Answer:
5n+30
Step-by-step explanation:
Answer:
D( 5n +30
Step-by-step explanation:
have a good day!:) sorry if I'm late
