You move up 4 units and right 2 units. You end at (-1, 3). Where did you start?
Answers
Answer:
You started at (-3,-1)
Related Questions
Question 15 2 pts If the coefficient of determination is 0.233, whal percentage of the dala line is explained? about the regression Homework Help: ZDB_Correlation coelficienLand coeticienLoLdeterminalion nolationand meanings = (PDF) 76.7% 46.6% 23.3% 5.43%
Answers
If the coefficient of determination is 0.233, then the percentage of data about the regression line explained is 23.3% , the correct option is (c) .
The coefficient of determination is defined as a statistical measure which represents the proportion of the variance in the dependent variable that is predictable from the independent variable.
An R-squared value of 0.233 means that 23.3% of the variance in the dependent variable can be explained by the independent variable.
In other words, about 23.3% of the data about the regression line is explained.
Therefore, the correct answer is (c) 23.3%.
Learn more about Coefficient Of Determination here
https://brainly.com/question/20263006
#SPJ4
The given question is incomplete , the complete question is
If the coefficient of determination is 0.233, what percentage of the data about the regression line is explained?
(a) 76.7%
(b) 46.6%
(c) 23.3%
(d) 5.43%
pls help i need asap
Translate the following word phrase into an algebraic equation.
“4 times a number increased by 7 is 27”
4(x + 7)=27
(x – 4) + 7=27
4x + 7=27
x ÷ 4 + 7=27
i think its 4+7=27
Answers
Answer:
4x+7=27
Step-by-step explanation: The answer you think is correct ! So the 4 times a number is 4x the four being a coefficient and X being the unknown number( variable ) and increase is adding so its +7 and is is just an another word for equal =
Find the probability that in 20 tosses of a fair six-sided die, a five will be obtained at least 5 times.
Answers
The probability that in 20 tosses of a fair six-sided die, a five will be obtained at least 5 times is approximately 0.3289 or 32.89%.
The probability of getting a 5 on any single toss of a fair six-sided die is 1/6. Since the tosses are independent, the number of 5's obtained in 20 tosses follows a binomial distribution with parameters n = 20 and p = 1/6.
We want to find the probability that a five will be obtained at least 5 times in 20 tosses. This is equivalent to finding the probability of getting 5, 6, 7, ..., or 20 fives in 20 tosses. We can use the binomial probability mass function to calculate these probabilities and then add them up.
Using a computer or a binomial probability distribution table, we can find the individual probabilities of getting k fives in 20 tosses for k = 5, 6, 7, ..., 20. We can then add up these probabilities to get the total probability of getting at least 5 fives in 20 tosses:
P(at least 5 fives) = P(5 fives) + P(6 fives) + ... + P(20 fives)
Using a computer or a binomial probability distribution table, we find that:
P(5 fives) ≈ 0.2029
P(6 fives) ≈ 0.0883
P(7 fives) ≈ 0.0270
P(8 fives) ≈ 0.0069
P(9 fives) ≈ 0.0015
P(10 fives) ≈ 0.0003
P(11 fives) ≈ 0.0001
P(12 fives) ≈ 0.0000
P(13 fives) ≈ 0.0000
P(14 fives) ≈ 0.0000
P(15 fives) ≈ 0.0000
P(16 fives) ≈ 0.0000
P(17 fives) ≈ 0.0000
P(18 fives) ≈ 0.0000
P(19 fives) ≈ 0.0000
P(20 fives) ≈ 0.0000
Summing up these probabilities, we get:
P(at least 5 fives) ≈ 0.3289
Therefore, the probability that in 20 tosses of a fair six-sided die, a five will be obtained at least 5 times is approximately 0.3289 or 32.89%.
Learn more about probability ,
https://brainly.com/question/30034780
#SPJ4
What is the X intercept of the equation y-1= -(x+5)?
Answers
Answer:
X-intercept is -4
Step-by-step explanation:
Solve
No links!!!
I will give brainlest
& send links get reported

Answers
Answer:
12 no .
x+2(4/5)=3(1/6)
x+5*2+4/5=6*3+1/6
x+14/5=19/6
5*x+14/5=19/6(do cross multiplication)
6(x+14)=19*5
6x+84=95
6x=95-84
x=11/6
Step-by-step explanation:
13 no
-0.4a+1.2=3.6
-0.4a=3.6-1.2
a=2.4/-0.4
a=-6
I have a late assignment Please help!!

Answers
The interquartile range for the data set are
Andre
Interquartile Range: = 2
For Lin
Interquartile Range = 8
For Noah
Interquartile Range = 8
How to fill the tableFor Andre
Min: 25 the minimum number
Q1: 27 (the third position)
Median: 28 (the sixth position)
Q3: 29 (the 9th position)
Max: 30 (the maximum number)
Interquartile Range: Q3 - Q1 = 29 - 27 = 2
For Lin
Min: 20 the minimum number
Q1: 21 (the third position)
Median: 28 (the sixth position)
Q3: 29 (the 9th position)
Max: 32 (the maximum number)
Interquartile Range: Q3 - Q1 = 29 - 21 = 8
For Noah
Min: 13 the minimum number
Q1: 15 (the third position)
Median: 20 (the sixth position)
Q3: 23 (the 9th position)
Max: 25 (the maximum number)
Interquartile Range: Q3 - Q1 = 23 - 15 = 8
Learn more about interquartile range at
https://brainly.com/question/4102829
#SPJ1
what expression has a value of 2/3
Answers
Answer:
(8 + 24) ÷ (12 x 4)
Step-by-step explanation:
Answer:
(8 + 24) ÷ ( 12 x 4 )
Step-by-step explanation:
32 / 48 = 2/3
Please help 60 points for a rapid answer-In the figure below which of the following is true in circle E?


Answers
Answer:
all 3 options are true : A, B, C
Step-by-step explanation:
warning : it has come to my attention that some testing systems have an incorrect answer stored as right answer for this problem.
they say that A and C are correct.
but I am going to show you that if A and C are correct, then also B must be correct.
therefore, my given answer above is the actual correct answer (no matter what the test systems say).
originally the information about the alignment of the point F in relation to point E was missing.
therefore, I considered both options :
1. F is on the same vertical line as E.
2. F is not on the same vertical line as E.
because of optical reasons (and the - incomplete - expected correct answers of A and C confirm that) I used the 1. assumption for the provided answer :
the vertical line of EF is like a mirror between the left and the right half of the picture.
A is mirrored across the vertical line resulting in B. and vice versa.
the same for C and D.
this leads to the effect that all 3 given congruence relationships are true.
if we consider assumption 2, none of the 3 answer options could be true.
but if the assumptions are true, then all 3 options have to be true.
now, for the "why" :
remember what congruence means :
both shapes, after turning and rotating, can be laid on top of each other, and nothing "sticks out", they are covering each other perfectly.
for that to be possible, both shapes must have the same basic structure (like number of sides and vertices), both shapes must have the same side lengths and also equally sized angles.
so, when EF is a mirror, then each side is an exact copy of the other, just left/right being turned.
therefore, yes absolutely, CAD is congruent with CBD. and ACB is congruent to ADB.
but do you notice something ?
both mentioned triangles on the left side contain the side AC, and both triangles in the right side contain the side BD.
now, if the triangles are congruent, that means that each of the 3 sides must have an equally long corresponding side in the other triangle.
therefore, AC must be equal to BD.
and that means that AC is congruent to BD.
because lines have no other congruent criteria - only the lengths must be identical.
ryan and betty both have 5 children in their family. their ages are ryan: 17, 12, 8, 4, 2 betty: 17, 16, 14, 11, 10 which group of children's ages have the greatest dispersion?
Answers
Betty's children have greater age dispersion than Ryan's children. Their ages range from 10 to 17, while Ryan's children range from 2 to 17.
Betty's children have the greatest dispersion. Dispersion refers to the extent to which the values in a set of data are spread out. The difference between the youngest and oldest child in Betty's family is 7 years, while the difference in Ryan's family is 15 years. The greater difference indicates a higher level of dispersion, meaning Betty's children have a greater range of ages and are spread out over a larger range of values than Ryan's children.
Learn more about Dispersion:
https://brainly.com/question/5001250
#SPJ4
£810 is divided between Paul, Brian & Colin so that Paul gets twice as much as Brian, and Brian gets three times as much as Colin. How much does Brian get.
Answers
Answer:
$486 (Paul)
$243(Brian)
$81(Colin)
Solving steps:
let Paul Be x, Brian be x,Colin be x
since Paul got twice as much as Brian which shows that brian and got three times
So Paul,= 3×2 so he got six times as much as the two others
while Brian got three times
and colins got once
so let's make an equation for this problem
=> 6x + 3x + x = $810
add 6 x + 3 x + x which give you 10 x
=> 10x = $810
divide both side by the coefficient of x
=> \( \frac{10x}{10} = \frac{810}{10} \)
=> \(x = \frac{810}{10} \)
=> x = 81
since you we have find what the value of x
insert into the previous equation which is
=> 6x + 3x + x
=> 6(81) = $486-----(for Paul)
3(81) = $243-------(for Brian)
(81) = $81 ---------(for Collin)
Find the area of the rectangle. The length is 1.25 and the width is 0.8 inches
Answers
The meal was $5.75 and you added a 15% tip
what was the tips total now.
Answers
Answer:
The tip was 0.86
Step-by-step explanation:
Connor is a 400m runner His median time is
Answers
Answer: 57.8
Step-by-step explanation:48.7 seconds + 49.3 seconds.= 57.8
A rectangular region has an area of 299 square miles. The length of the region is 10 miles longer than its width. Find the length and width of the region.
Answers
Answer:
Let's represent the width of the region by "w". According to the problem, the length of the region is 10 miles longer than the width, so we can represent the length as "w + 10".
The formula for the area of a rectangle is:
Area = Length x Width
So we can write an equation for the area of this region:
299 = (w + 10) x w
Expanding the right side, we get:
299 = w^2 + 10w
Now we can rearrange this equation into standard quadratic form:
w^2 + 10w - 299 = 0
We can solve for "w" by using the quadratic formula:
w = (-b ± sqrt(b^2 - 4ac)) / 2a
Where a = 1, b = 10, and c = -299. Plugging in these values, we get:
w = (-10 ± sqrt(10^2 - 4(1)(-299))) / 2(1)
w = (-10 ± sqrt(1180)) / 2
w = (-10 ± 34.351) / 2
We can ignore the negative solution, since the width of the region cannot be negative. So the width is:
w = (-10 + 34.351) / 2
w = 12.176
We can round the width to the nearest mile, since we can't have a fractional width. So the width is approximately 12 miles.
Now we can use the equation we derived earlier to find the length:
299 = (w + 10) x w
299 = (12 + 10) x 12
299 = 22 x 12
So the length is 22 miles.
Therefore, the width of the region is approximately 12 miles and the length is 22 miles.
What is an angle that is supplementary to BGD

Answers
Answer:
DGE and BGA
Step-by-step explanation:
Supplementary angles are two angles whose measures add up to 180°
so BGD + DGE = 180 or BGD + BGA = 180
so both DGE and BGA are supplementary to BGD
Find the value of x if PQRS is a rhombus
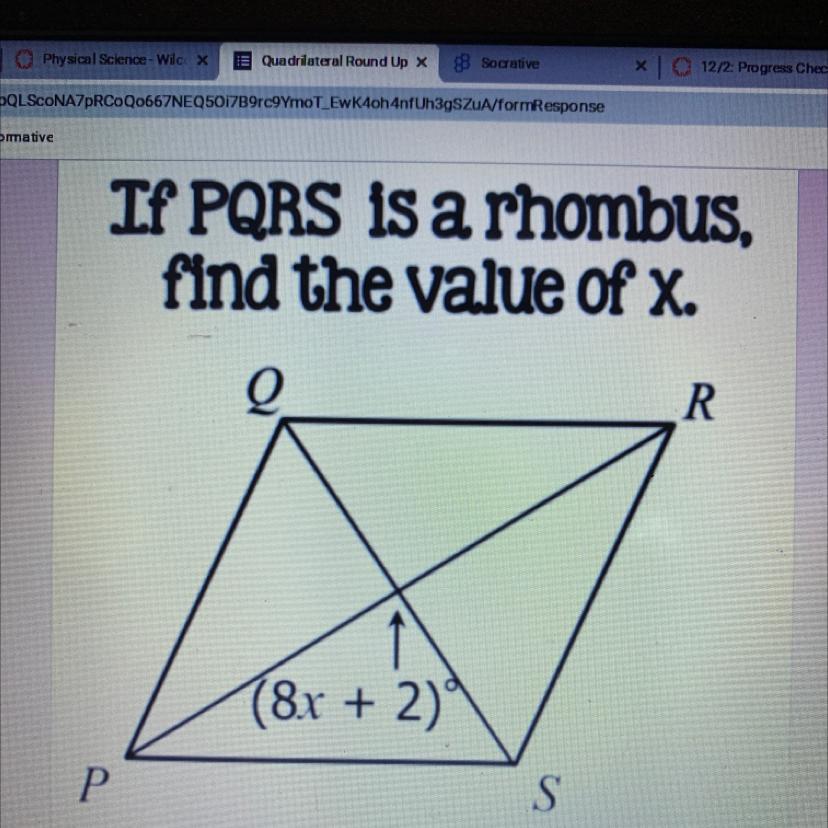
Answers
I know for sure. Just did this unit
Answer:
x = 11
Step-by-step explanation:
The diagonals of a rhombus are perpendicular bisectors of each other, thus
8x + 2 = 90 ( subtract 2 from each side )
8x = 88 ( divide both sides by 8 )
x = 11
Simplify the expression 8a - 6b -3a + 2b
Answers
Answer:
5a - 4b
Step-by-step explanation:
= 8a - 6b - 3a +2b
= 8a - 3a - 6b + 2b
= 5a - 4b
Hope it helps :)
Answer:
5a - 4b
Step-by-step explanation:
In a group of 120 recruits at the police academy 80 are college graduates and 25 are army veterans. If 15 of the recruits are both college graduate and army veterans as shown above, how many are neither college graduate nor army veterans?
Answers
Answer:
the number of recruits neither be college graduate and nor army veterans is 30
Step-by-step explanation:
The computation of the number of recruits neither be college graduate and nor army veterans is as follows;
= Total recruits - (college students + army veterans - both college graduates & army veterans)
= 120 recruits - (80 + 25 - 15)
= 120 recruits - 90
= 30
hence, the number of recruits neither be college graduate and nor army veterans is 30
Multiply the polynomials. (2x+y)·(4x^2-2xy+y^2)
Answers
Answer:
Step-by-step explanation:
The answer is 4x^2y+8x^3+y^2-2xy
which of the following is the best description of a population that has a stable age distribution? responses a large population that is growing at a constant rate a large population that is growing at a constant rate a large population with a negative growth rate a large population with a negative growth rate a population that is in the early stages of logistic population growth a population that is in the early stages of logistic population growth a growing population in which the proportions of individuals in the different age classes remain constant a growing population in which the proportions of individuals in the different age classes remain constant a small population that has not yet achieved exponential growth
Answers
the best description of a population that has a stable age distribution is (e) a growing population in which the proportions of individuals in the different age classes remain constant.
What does it mean to have a stable age distribution?Such a population will have a steady age distribution since the proportion of people in each age group will remain constant. Independent of the initial age distribution is this steady age distribution and is solely dependent on maintaining stable fertility and death rates.
It has been demonstrated that a closed population's annual rate of increase tends to become constant when it is exposed to age-specific fertility and mortality rates for a considerable amount of time.
A population that has reached this point is referred to as stable, and this consistent rate of growth is known as the intrinsic rate of natural increase.
Such a population will have a steady age distribution since the proportion of people in each age group will remain constant.
to learn more about stable age distribution visit:
brainly.com/question/29762197
#SPJ1
1/3 x + y = 4 solve for y
Answers
hope this helps :)
The simplified answer to the equation is \(y=-\frac{1}{3}x+4\)
First, subtract \(\frac{1}{3}x\) on both sides.
\(y=-\frac{1}{3}x+4\)
You have isolated \(y\) by itself, and the equation can't be simplified further, so \(y=-\frac{1}{3}x+4\) is your answer.
jared has a wooden board 11 ft long. he wants to cut it into two pieces so that the longer piece is 4 ft less than 4 times the length of the shorter piece. how long will each piece of board be? enter your answers in the boxes.
Answers
On solving we got that. he shorter pieces will therefore be 3 feet long and the longer pieces will therefore be 8 feet long.
What is equation?Since equations are essentially questions, efforts to systematically find answers to those questions have been the driving force behind the development of mathematics. From straightforward algebraic equations that just require addition or multiplication to differential equations, exponential equations that use exponential expressions, and integral equations, there are many different types of equations that range in complexity.
The lengths of the shorter and longer pieces of a board should be determined.
the case
Let's say that the shorter parts are x in length.
as stated
Jared has an 11-foot wooden board with him.
In order for the longer piece to be 4 feet less than 4 times as long as the shorter piece, he wants to cut it into two pieces.
The length of the longer pieces is then equal to 4x - 4.
The equation then becomes
\(x + 4x - 4 = 11\\ 5x = 11 + 4\\ 5x = 15\\ x = 3 ft\)
The shorter pieces will therefore be 3 feet long.
The longer pieces' length -
\(4x - 4\\ = 4 X 3 - 4\\ = 12 - 4\\ = 8 ft\)
The longer pieces will therefore be 8 feet long.
To know more about equation visit:
https://brainly.com/question/649785
#SPJ4
how deep would a water container have to be to have the same pressure at the bottom as that found at the bottom of a 10.0 -cm deep beaker of mercury, which is 13.55 times as dense as water
Answers
A 10 cm deep beaker mercury will have the same hydrostatic pressure as 133.5 cm deep water.
The hydrostatic pressure exerted by a fluid is given by:
P = ρ.g.h
Where:
ρ = fluid density
g = gravitational acceleration
h = fluid depth
We want to compare 2 types of fluid, water and mercury.
Divide both sides of the equation by h
P/h = ρ.g
Since pressure is held constant, then the fluid density is inversely proportional to the fluid depth.
Therefore,
h_water : h_mercury = ρ_mercury : ρ_water
Given that:
ρ_mercury = 13.55 ρ_water and h_mercury = 10 cm
Then,
h_water : 10 = 13.55 ρ_water : ρ_water
h_water : 10 = 13.55 : 1
h_water = 13.55 × 10 = 135.5 cm
Learn more about hydrostatic pressure here:
https://brainly.com/question/11758621
#SPJ4
Change from radians to degrees 7pi/4
Answers
The conversion of \(\dfrac{7\pi}{4}\) in degrees will be equal to 315°
What is a radian?Radian is a unit of angle, equal to an angle at the centre of a circle whose arc is equal in length to the radius.
Here the given angle in radian is \(\dfrac{7\pi}{4}\)
Angle in degrees is converted by multiplying it with \(\dfrac{180}{\pi}\).
So the angle in degrees will be:-
\(=\dfrac{7\pi}{4}\times \dfrac{180}{\pi}\)
\(=\dfrac{7\times 180}{4}\)
Angle=315°
Therefore the conversion of \(\dfrac{7\pi}{4}\) in degrees will be equal to 315°
To know more about radian follow
https://brainly.com/question/19758686
#SPJ1
Score on last try: 0 of 10 pts. See Details for more. You can retry this question below A random sample of 750 Democrats included 615 that consider protecting the environment to be a top priority A random sample of 850 Republicans included 306 that consider protecting the environment to be a top priority, Construct a 99% confidence interval estimate of the overall difference in the percentages of Democrats and Republicans that prioritize protecting the environment. (Give your answers as percentages, rounded to the nearest tenth of a percent.) Answers: The margin of error is 0.0638% We are 99% confident that the difference between the percentage of Democrats and Republicans who prioritize protecting the environment lies between
Answers
The 99% confidence interval estimate of the overall difference in the percentages of Democrats and Republicans that prioritize protecting the environment is, (0.407, 0.513).
We can use the formula for the 99% confidence interval estimate of the overall difference in the percentages of Democrats and Republicans that prioritize protecting the environment,
CI = (p1 - p2) ± z √((p₁(1-p₁)/n1) + (p₂(1-p₂)/n₂))
where: p₁ = proportion of Democrats that prioritize protecting the environment p₂ = proportion of Republicans that prioritize protecting the environment n₁ = sample size of Democrats n₂ = sample size of Republicans z = z-score for a 99% confidence interval which is 2.576)
Using the values given in the problem,
CI = (615/750 - 306/850) ± 2.576(((615/750)(1-615/750)/750) + ((306/850)(1-306/850)/850))
= (0.82 - 0.36) ± 2.576√((0.82(1-0.82)/750) + (0.36(1-0.36)/850))
= 0.46 ± 0.053
therefore, the 99% confidence interval estimate of the overall difference in the percentages of Democrats and Republicans that prioritize protecting the environment is (0.407, 0.513).
Learn more about the standard deviation visit:
https://brainly.com/question/475676
#SPJ4
The pseudoinverse of the null (all zero) vector is the transposed null vector. The pseudoinverse of a non-nullvector is the conjugate transposed vector divided by its squared magnitude:x+ = { 0,. if x = 0;x-1 otherwise.
Answers
What is a pseudoinverse?
The pseudoinverse of the null (all zero) vector is indeed the transposed null vector. This is because the null vector has no direction or magnitude, so when we calculate its pseudoinverse, we are essentially looking for a vector that when multiplied with the null vector gives us the identity matrix. Since there is no such vector, the pseudoinverse is simply the transposed null vector.However, for a non-null vector, the pseudoinverse is calculated using a different formula. Specifically, the pseudoinverse of a non-null vector x is given by the conjugate transposed vector divided by its squared magnitude.
This is denoted by x+ and is defined as follows:
x+ = {0, if x = 0; x*-/(||x||^2), otherwise.
Here, x* denotes the conjugate transpose of x, and ||x||^2 represents the squared magnitude of x. Essentially, we are finding a vector that when multiplied with x gives us the identity matrix (or as close to it as possible). This vector is the pseudoinverse, and it is computed using the formula above.
So in summary, the pseudoinverse of the null vector is the transposed null vector, while the pseudoinverse of a non-null vector is the conjugate transposed vector divided by its squared magnitude.
To learn more about ''The pseudoinverse of the null (all zero) vector'' visit : https://brainly.com/question/15297129
#SPJ11
Solve for b
32 = 12 + 5/6b
Answers
Answer:
b=24, please give Brainliest if this helped you
Step-by-step explanation:

Evaluate the function. f(x) = 3x² – x Find f(10)
Answers
Answer:
f(10)=290
Step-by-step explanation:
Function Evaluation
Given a function f(x) as an explicit expression, finding f(x=a) implies substituting the value of x by a in every instance it occurs.
We are given the function:
\(f(x)=3x^2-x\)
It's required to find f(10). We replace the x for 10:
\(f(10)=3*10^2-10\)
Operating:
\(f(10)=3*100-10\)
\(f(10)=300-10\)
\(f(10)=290\)
Thus, f(10)=290
Jamal borrowed $15 600 for 6 years from a bank. The annual simple interest rate for the first 3 years is 1.6%. From then onward, the annual simple interest rate is increased to 2%. How much interest will he owe at the end of 6 years?
Answers
Answer:
the interest owed is 1684.8
Step-by-step explanation:
Formula for simple interest =
I = Prt, where P is amount borrowed, r for interest rate and t for time.
Since the first three years is 1.6% interest we can write:
I = 15600 x 0.016 x 3
= 748.8
Then for the following 3 years the interest rate is 2%:
I = 15600 x 0.02 x 3
= 936
Adding the values gives us 1684.8
A company finds that the marginal profit, in dollars per foot, from drilling a well that is x feet deep is given by P′(x)=4 ^3√ x. Find the profit when a well 50 ft deep is drilled.
Question content area bottom Part 1 Set up the integral for the total profit for a well that is 50 feet deep.
P(50)= ∫ enter your response here dx
Part 2 The total profit is $enter your response here. (Round to two decimal places as needed.)
Answers
The total profit when a well 50 feet deep is drilled is approximately $1164.10, rounded to two decimal places.
The total profit for drilling a well that is 50 feet deep need to integrate the marginal profit function P'(x) with respect to x from 0 to 50.
This gives us the total profit function P(x):
P(x) = ∫ P'(x) dx from 0 to 50
Substituting P'(x) = \(4 \times x^{(1/3)\) into the integral we get:
P(x) = \(\int 4 \times x^{(1/3)\) dx from 0 to 50
Integrating with respect to x get:
P(x) = 4/4 * 3/4 * x^(4/3) + C
C is the constant of integration.
The value of C we need to use the given information that the marginal profit is zero when the well is 0 feet deep.
This means that the total profit is also zero when the well is 0 feet deep.
P(0) = 0
= \(4/4 \times 3/4 \times 0^{(4/3)} + C\)
C = 0
So the total profit function is:
P(x) = \(3x^{(4/3)\)
The profit when a well 50 feet deep is drilled is:
P(50) = \(3 \times 50^{(4/3)\) dollars
Using a calculator to evaluate this expression, we get:
P(50) = \(3 \times 50^{(4/3)\)
≈ $1164.10
For similar questions on profit
https://brainly.com/question/26483369
#SPJ11