you pay $175 for 5 football tickets. How much will you for each (1) ticket?
Answers
Answer:
Step-by-step explanation:
175 ÷ 5 = 35
$35 per ticket
Answer:
35
Step-by-step explanation:
It's cuz you want to know how much one ticket costs right?
Sp do 175 divded by 5
You should get 35 as the answer!
Related Questions
translations can be moved along an vector at any time and still result in the same image true or false ?
Answers
Answer:
True................
Answer:
True
Step-by-step explanation:
Find the values of x and y
X=
Y=

Answers
Answer:
x = 7
y = 4
Step-by-step explanation:
y + 12 = 3x - 5
5y - 4 = 3x - 5
So y + 12 = 5y - x
To solve the equation above, y =4
Sub y = 4,
x = 7
Organizational culture is set by a. the manager b. the ethics committee c. the engineer d. none of the given options
Answers
Organizational culture is defined as the common beliefs, values, attitudes, customs, behaviors, and traditions that characterize a specific organization and determine the manner in which it functions. Organizational culture is set by the manager.
In a corporate or business environment, organizational culture can influence the daily operations of employees. It is the responsibility of managers to create a positive culture that emphasizes teamwork, respect, integrity, and accountability. The manager is an essential individual responsible for establishing and maintaining the organization's culture, which will ultimately define the employee's attitudes, behaviors, and productivity levels. He or she sets the tone for the workplace by creating an environment that fosters collaboration, innovation, and success. Employees need to feel connected to their workplace and colleagues to be motivated to do their best work. If a manager promotes a culture of fear, competition, or dishonesty, employees may become unmotivated or unproductive. An effective manager understands the importance of creating a positive workplace culture and works hard to establish and maintain it. Managers can establish a positive culture by encouraging open communication, providing regular feedback and recognition, fostering a sense of teamwork, creating opportunities for professional development, and setting high standards for performance. Managers must lead by example and demonstrate the behaviors and attitudes that they expect from their employees. They must hold themselves and others accountable for their actions, communicate expectations clearly, and provide support when needed. A positive organizational culture will enable an organization to attract and retain top talent, increase employee engagement, and promote collaboration and innovation.
To know more about Organizational culture visit:
https://brainly.com/question/28503044
#SPJ11
suppose one of the six is a doctor who must sit on the aisle in case she is paged. how many ways can the people be seated together in the row with the doctor in an aisle seat?
Answers
We make use of permutation formula to find out that there are a total of 240 ways in which the people can be seated together in the row with the doctor in an aisle seat.
It is given to us that -
There are six people
One of the six is a doctor who must sit on the aisle in case she is paged.
We have to find out the number of ways in which the people can be seated together in the row with the doctor in an aisle seat.
From the given information it is known that the doctor is seated in an aisle seat.
So, the doctor can be seated in the extreme left side of the aisle. This implies that in this case, the total ways to be seated = 5!.
Similarly, it can also be said that the doctor can be seated in the extreme right side of the aisle. This implies that in this case, the total ways to be seated = 5!.
Thus, the total number of ways in which the people can be seated together in the row with the doctor in an aisle seat = 2 * 5!
= 2 * 5 * 4 * 3 * 2 * 1
= 240 ways
Therefore, through permutation we can conclude that there are a total of 240 ways in which the people can be seated together in the row with the doctor in an aisle seat.
To learn more about permutation visit https://brainly.com/question/1216161
#SPJ4
Find the general solution of the following differential equation. Primes denote derivatives with respect to x. 3x2y' + 6xy = 15y3
Answers
The required general solution of the differential equation in implicit form y = \([(3/2) * (15x + C) * x^{-3}]^{-3/2}\).
How to find general solution of the differential equation?The differential equation is a nonlinear equation and cannot be solved exactly by standard methods. One way to approach a solution is to try to find a substitution that transforms the equation into a separable form, where the variables can be separated and integrated separately. A common approach is to make the substitution y = v^(-2/3), which transforms the equation into:
According to question:3x^2 * (2/3) * v^(-5/3) * v' + 6x * v^(-2/3) = 15 * v^(-5/3)
Dividing both sides by v^(-5/3), we get:
3x^2 * (2/3) * v' + 6x * 3 * (2/3) * v^(1/3) = 15
This is now a separable differential equation, and we can integrate both sides to find the general solution:
∫(3x^2 * (2/3) * v' dx) = ∫(15 dx) + C
(2/3) * x^3 * v = 15x + C
v = (3/2) * (15x + C) * x^(-3)
Finally, substituting back for y = v^(-2/3), we get the general solution:
y = \([(3/2) * (15x + C) * x^{-3}]^{-3/2}\)
This is the general solution of the differential equation in implicit form. To find an explicit form, one could solve for C using initial or boundary conditions.
To know more about differential equation visit:
brainly.com/question/14620493
#SPJ4
help please and thank you

Answers
Answer:
120 cars
Step-by-step explanation:
The given function is
\(C(x)=0.5x^2-120x+21,481\)
and its parent function would be
\(f(x)=ax^2+bx+c\)
So,
\(a=0.5\)
\(b = -120\)
and
\(c = 21,481\)
The minimum cost would be found using:
\(x = -\frac{b}{2a}\)
So just input a and b into the function:
\(x= -\frac{-120}{2(0.5)}\)
\(x=-\frac{-120}{1}\)
\(x = 120\)
Therefore there must be 120 cars made to minimize the cost.
A sprinkler set in the middle of a lawn sprays in a circlular pattern the area of the lawn that gets sprayed by the sprinkler can be described by the equation (x-2)y+(y-5)2=169
Answers
To see why, we can rewrite the equation in standard form for a circle:
(x-2)y+(y-5)²=169
xy - 2y + y² - 10y + 25 = 169
x(y-2) + y² - 10y - 144 = 0
(x-(-2))(y-5)² = 144
(x+2)(y-5)² = 144
This is the equation of a circle with center (-2, 5) and radius 12. Therefore, the area of the lawn that gets sprayed by the sprinkler is a circle with center (-2, 5) and radius 12.
HOMEWORK 2.6 FOR FIND THE FOLLOWING FUNCTIONS
= Homework: Homework 2.6 X+4 For f(x)=2x-4 and g(x) = 2 a. (fog)(x); b. (gof)(x); c. (fog)(7); d. (gof)(7) a. (fog)(x) = (Simplify your answer.) find the following functions.
Answers
To find the composite functions (fog)(x) and (gof)(x) using the given functions f(x) = 2x - 4 and g(x) = 2, we substitute one function into the other based on the order indicated. (fog)(x) = 0, (gof)(x) = 2, (fog)(7) = 0, and (gof)(7) = 2.
The value of (fog)(7) and (gof)(7) can be determined by evaluating the composite functions at x = 7.
a. To find (fog)(x), we substitute g(x) into f(x): (fog)(x) = f(g(x)) = f(2). Since g(x) = 2, we replace g(x) with 2 in f(x): f(2) = 2(2) - 4 = 4 - 4 = 0. Therefore, (fog)(x) = 0.
b. To find (gof)(x), we substitute f(x) into g(x): (gof)(x) = g(f(x)) = g(2x - 4). Since f(x) = 2x - 4, we replace f(x) with 2x - 4 in g(x): g(2x - 4) = 2. Therefore, (gof)(x) = 2.
c. To find (fog)(7), we evaluate (fog)(x) at x = 7: (fog)(7) = 0.
d. To find (gof)(7), we evaluate (gof)(x) at x = 7: (gof)(7) = 2.
Therefore, (fog)(x) = 0, (gof)(x) = 2, (fog)(7) = 0, and (gof)(7) = 2.
Learn more about composite functions here :
https://brainly.com/question/30143914
#SPJ11
If 6 cans of tomatoes cost $9, how much would it cost to buy 8 cans?
Answers
Answer:
$12
Step-by-step explanation:
Cans : Dollars
6 cans : 9 dollars
DIVIDE BY 3
2 cans : 3 dollars
MULTIPLY BY 4
8 cans : 12 dollars
Hope this helps :)
Have a great day!
Find the volume of the figure. Round to the
nearest tenth.
1,286.1 units
401.9 units
5,144.6 units
128.6 units

Answers
Answer:
1,286.1 units is the answer
Step-by-step explanation:
your answer may vary depending on what you use for pie, using a calculator with pie on it gave me approx. 1286.79635
volume formula: V=πr^2h
so π*6.4^2*h
π*40.96*10
3.14*409.6
1,286.144
round
1,286.1
Write an expression for 57 less than j
Answers
Answer:
Step-by-step explanation:
j-50
In 3 hours, the Johnson family traveled 195 miles by car. How far will they travel in 5 hours?
Giving away 40 points please answer
Answers
The distance covered by by the Johnson family in 5 hours is 325 miles
In the above question, it is given that
Johnson family is travelling,
The distance covered in 3 hours = 195 miles
We need to find the distance covered by the Johnson family in 5 hours
So, first we'll find the distance covered by the Johnson family in 1 hours
Therefore,
The distance covered in 1 hour = \(\frac{195}{3}\) miles
Now, the distance covered in 5 hours = \(\frac{195 . 5 }{3}\) miles
= 325 miles
Hence, the distance covered by by the Johnson family in 5 hours is 325 miles
To learn more about, distance, here
https://brainly.com/question/15256256
#SPJ1
Angle b = 90 degrees, side bc = 20, angle y = 90 degrees, and side yz = 20. what additional information would you need to prove that δabc ≅ δxyz by hl? angle a is congruent to angle x. angle b is congruent to angle y. side ab is congruent to side xy. side ac is congruent to side xz.
Answers
Answer:
D) Side AC is congruent to side XZ.
Step-by-step explanation:
If triangle ABC is congruent to triangle XYZ then:
AB = XYBC = YZAC = XZm∠A = m∠Xm∠B = m∠Ym∠C = m∠ZIn triangle ABC:
m∠B = 90°BC = 20In triangle XYZ:
m∠Y = 90°YZ = 20Therefore, one of the corresponding angles is a right angle, which means both triangles are right triangles. Also, one of the corresponding legs of the two triangles is congruent.
The Hypotenuse-Leg Triangle Congruence Theorem (HL) states that if the hypotenuse and one leg of a right triangle are congruent to the corresponding parts of another right triangle, then the two triangles are congruent.
Therefore, to prove congruence by HL, we would need the hypotenuses of both triangles to be congruent.
The hypotenuse of a right triangle is the side opposite the right angle.
Therefore, the hypotenuses of the two triangles are:
Hypotenuse of ΔABC = ACHypotenuse of ΔXYZ = XZSo the additional information we would need to prove that ΔABC ≅ ΔXYZ by HL is:
Side AC is congruent to side XZ.Find the value of x if 212x5 is a multiple of 3 and 11 please find out now guys HELP!
Answers
Answer:
x = 8
Step-by-step explanation:
If the number 212x5 is a multiple of 3, the sum of the digits needs to be a multiple of 3, so we have:
2 + 1 + 2 + x + 5 = 10 + x
The value of x can be 2, 5 or 8
If the number is a multiple of 11, we have to calculate the first number minus the second, plus the third, minus the fourth... and so on, and the result needs to be a multiple of 11. So we have:
2 - 1 + 2 - x + 5 = 8 - x
x needs to be 8, so we have 8 - 8 = 0, that is a multiple of 11.
So the value of x is 8.
how to make a calculator in c# windows form application
Answers
To create a calculator in a C# Windows Form application, you can follow these steps:
1. Open Visual Studio and create a new Windows Forms Application project.
2. Design the user interface of the calculator by dragging and dropping the necessary controls from the Toolbox onto the form. You will need buttons for numbers, arithmetic operations (+, -, *, /), and an equals (=) button. You can also add a text box to display the result.
3. Set properties for each control to specify their appearance and functionality. For example, you can set the text property of each button to represent the corresponding number or operation.
4. Write the code for handling button clicks and performing calculations. Double-click on each button to create an event handler for the Click event. Inside the event handler, you can access the button's text property to determine which button was clicked. Use conditional statements and switch-case statements to handle different button clicks.
5. Create variables to store the numbers entered by the user and the result of the calculations. You can use the double data type for these variables.
6. Implement the logic for performing calculations based on the button clicked. For example, when the "+" button is clicked, you can add the two numbers together and display the result in the text box. Similarly, you can handle other arithmetic operations.
7. Use the TryParse method to convert the button's text to a double value and store it in the appropriate variable. This will allow you to perform calculations correctly.
8. Display the result of the calculations in the text box by assigning the calculated value to the text property of the text box.
9. Test your calculator by running the application and clicking on the buttons to perform calculations. Verify that the calculator performs the desired calculations and displays the correct results.
Here is a simplified example of code for handling button clicks and performing calculations in a C# Windows Form application:
```csharp
private double firstNumber;
private double second number;
private string operation;
private void NumberButton_Click(object sender, EventArgs e)
{
Button button = (Button)sender;
textBox.Text += button.Text;
}
private void OperationButton_Click(object sender, EventArgs e)
{
Button button = (Button)sender;
operation = button.Text;
firstNumber = double.Parse(textBox.Text);
textBox.Clear();
}
private void EqualsButton_Click(object sender, EventArgs e)
{
secondNumber = double.Parse(textBox.Text);
double result = 0;
switch (operation)
{
case "+":
result = firstNumber + secondNumber;
break;
case "-":
result = firstNumber - secondNumber;
break;
case "*":
result = firstNumber * secondNumber;
break;
case "/":
result = firstNumber / secondNumber;
break;
}
textBox.Text = result.ToString();
}
```
Remember to adjust the code and customize the user interface according to your specific requirements.
to know more about c# windows here:
brainly.com/question/31252564
#SPJ11
Please, multiply the following Algebric sum.........
3ab+2bc, 5bc
Answers
Answer: The required product of two given algebraic expressions =15abc +10b²c²
Step-by-step explanation:
Here we need to multiple two algebraic expressions: 3ab+2bc, 5bc
i.e. The required product = (3a+2bc) x (5bc)
= 3a x 5bc + 2bc x 5bc [Using right distributive property: (a+b)c= ac+bc]
= (3x 5) abc + (2 x 5) (bc)²
= 15abc +10b²c²
Therefore, the required product of two given algebraic expressions = 15abc +10b²c²
The graph shows the solution to which system of equations?

Answers
Answer:
C) y = 2x - 3 and y = -2x - 1.
Hope this helps you!
Discussion Topic
The equation y = kx represents a proportional relationship between x and y, where k is
the constant of proportionality. For a moving object, the equation d = st represents a
proportional relationship between distance (d) and speed (s) or between distance (a)
and time (1). Explain the different ways that you can define the constant of
proportionality for this equation. Then describe some other equations that represent
proportional relationships in the real world and explain why they're useful. Research on
the internet, if needed.
Answers
Proportional relationships in real world settings are given as follows:
Distance and time: d = st, velocity is the constant.Time and distance: one divided by the velocity is the constant.Velocity and distance: one divided by the time is the constant.What is a proportional relationship?A direct proportional relationship is modeled as follows:
y = kx.
In which:
y is the output variable.k is the constant of proportionality.x is the input variable.One example is the relation between distance, velocity and time, given as follows:
d = st.
In which the velocity is the constant.
This relationship can also be interpreted as proportional between distance and velocity, with time as constant.
Another format of this relationship is:
t = d/s
Which means that time and distance are proportional, which one divided by the velocity as the constant.
Velocity and distance can also be proportional, as follows:
s = d/t.
With one divided by the time as constant.
More can be learned about proportional relationships at https://brainly.com/question/10424180
#SPJ1
In a plane if a line is ____ to one of the two parallel lines then it is perpendicular to the other

Answers
Recall the following information:
1) In a plane, two lines that are parallel exist on the same axis.
2) Hence, any line which is perpendicular to one of two parallel lines is also perpendicular to the other.
3) This concept is evident in the model of ladders, where each of the vertical lines is perpendicular to the parallel step lines(horizontal lines).
With this information, it can be said that if a line is perpendicular to one of two parallel lines, then it is perpendicular to the other.
T
Vectors u and v are shown on the graph.Part A: Write u and v in component form. Show your work. (3 points)Part B: Find u + v. Show your work. (2 points)Part C: Find 5u − 2v. Show your work. (5 points)

Answers
ANSWER
\(\begin{gathered} (A)u<9,7>;v<8,-2> \\ (B)<17,5> \\ (C)<29,39> \end{gathered}\)EXPLANATION
(A) We want to write the vectors in component form.
To do this, we will write them in terms of their horizontal and vertical lengths.
To do this, we have to find the difference between the coordinate points of the endpoints and the starting points of the vectors.
Hence, for vector u, its starting point is (2, -6) and its endpoint is (11, 1).
Hence, its component form is:
\(\begin{gathered} <11,1>-<2,-6> \\ \Rightarrow<11-2,1-(-6)> \\ \Rightarrow<9,1+6> \\ <9,7> \end{gathered}\)For the vector v, its starting point is (5, 8) and its endpoint is (13, 6).
Hence, its component form is:
\(\begin{gathered} <13,6>-<5,8> \\ \Rightarrow<13-5,6-8> \\ \Rightarrow<8,-2> \end{gathered}\)Hence, the component form of the vectors is:
\(\begin{gathered} u<9,7> \\ v<8,-2> \end{gathered}\)(B) To find the sum of the two vectors, we have to find the sum of their components.
That is:
\(\begin{gathered} u+v=<9,7>+<8,-2> \\ \Rightarrow<9+8,7+(-2)> \\ <17,7-2> \\ <17,5> \end{gathered}\)That is the answer.
(C) To find 5u - 2v, we have to multiply vector u by 5, multiply vector v by 2, and then find the difference:
\(\begin{gathered} 5\lbrack<9,7>\rbrack-2\lbrack<8,-2>\rbrack \\ \Rightarrow<45,35>-<16,-4> \\ \Rightarrow<45-16,35-(-4)> \\ \Rightarrow<29,35+4> \\ \Rightarrow<29,39> \end{gathered}\)That is the answer.
Calculate how much interest is earned on a deposit of $10000 after 10 years if interest was paid at 4.5% per year compounded monthly. Layout all work.
Answers
The interest earned on a deposit of $10,000 after 10 years with an interest rate of 4.5% compounded monthly is approximately $4,842.43.
To calculate the interest earned on a deposit of $10,000 after 10 years with an interest rate of 4.5% per year compounded monthly, we can use the formula for compound interest:
A = P(1 + r/n)^(nt)
Where:
A is the final amount (including both principal and interest)
P is the principal amount (initial deposit)
r is the annual interest rate (as a decimal)
n is the number of times interest is compounded per year
t is the number of years
In this case, the principal amount (P) is $10,000, the annual interest rate (r) is 4.5% or 0.045 as a decimal, the interest is compounded monthly (n = 12), and the time period (t) is 10 years.
Plugging these values into the formula, we have:
A = 10000(1 + 0.045/12)^(12*10)
Simplifying the exponent and evaluating the expression:
A = 10000(1 + 0.00375)^(120)
A = 10000(1.00375)^(120)
Using a calculator, we find:
A ≈ 14842.43
The final amount (A) after 10 years is approximately $14,842.43.
To calculate the interest earned, we subtract the principal amount from the final amount:
Interest = A - P
Interest = 14842.43 - 10000
Interest ≈ 4842.43
Learn more about interest rate here :-
https://brainly.com/question/28236069
#SPJ11
Let a < b. Find the crossing point n0 at which c1na = c2nb, for any
c1; c2.
b) As before, let a < b. Prove that nb+na and nb become arbitrarily close
as n grows larger (i.e., na becomes irrelevant).
(Design and Analysis of Algorithms homwork)
Answers
a. The crossing point n0 at which c1 * n^a = c2 * n^b is given by n0 = 10^(-log(c1 / c2) / (a - b)).
b. as n grows larger, nb and nb+na become arbitrarily close, and the term na becomes irrelevant in the comparison.
a. To find the crossing point n0 at which c1 * n^a = c2 * n^b, where a < b and c1, c2 are constants, we can solve the equation:
c1 * n^a = c2 * n^b
Dividing both sides by n^b, we get:
(c1 / c2) * n^(a-b) = 1
Taking the logarithm of both sides, we have:
log((c1 / c2) * n^(a-b)) = log(1)
Using logarithmic properties, we can simplify the equation:
log(c1 / c2) + (a - b) * log(n) = 0
Now, solve for n:
log(n) = -log(c1 / c2) / (a - b)
Taking the antilogarithm of both sides, we obtain:
n = 10^(-log(c1 / c2) / (a - b))
Therefore, the crossing point n0 at which c1 * n^a = c2 * n^b is given by n0 = 10^(-log(c1 / c2) / (a - b)).
b) To prove that nb+na and nb become arbitrarily close as n grows larger (i.e., na becomes irrelevant), we can compare the growth rates of nb+na and nb.
Let's take the ratio of nb+na to nb:
(nb+na) / nb = (n^b * n^a) / n^b = n^a
As n grows larger, the dominant term in the ratio (nb+na) / nb is n^a.
Since a < b, as n grows larger, the term n^a becomes less significant compared to n^b. In other words, nb dominates nb+na.
Therefore, as n grows larger, nb and nb+na become arbitrarily close, and the term na becomes irrelevant in the comparison.
Learn more about logarithm at https://brainly.com/question/12049968
#SPJ11
An arithmetic sequence is given below.
14, 11, 8 , 5 , ...
Write an explicit formula for the n^th term a(n).
help me understand this plzz, no file just answer
Answers
Answer:
a(n)= a + (n - 1)d
a(n) = 17 - 3n
Step-by-step explanation:
14, 11, 8 , 5 , ...
The given sequence above is an Arithmetic sequence and the explicit formula is given as:
a(n) = a + (n - 1)d
Where
a = First term = 14
n = number of terms
d = common difference
The common difference =
Second term - First term or Third term - Second term
= 11 - 14 or 8 - 11 or 5 - 8
= -3
Therefore, the explicit formula for the nth term a(n) is written as:
a(n) = 14 + (n - 1)-3
a(n) = 14 -3n + 3
a(n) = 14 + 3 - 3n
a(n) = 17 - 3n
The explicit formula a(n) =
a(n) = 17 - 3n
"Am I solving it the right way? If so, why can't I get the exact
answer?
1) ex 1.a Find the value of e² = A 1.b Find the value of T5(2) the 5th degree polynomial of ex = B 1.
Answers
The value of e² is approximately 7.389056 and the value of T5(2), the 5th degree polynomial of e^x, depends on the coefficients of the polynomial.
1.a) The value of e² can be found by evaluating e raised to the power of 2. The constant e is a mathematical constant approximately equal to 2.71828. When e is squared, the result is approximately 7.389056.
1.b) The expression T5(2) represents the 5th degree polynomial of e^x, where x is equal to 2. The specific value of T5(2) depends on the coefficients of the polynomial. In general, a polynomial of degree n can be represented as a sum of terms, each term consisting of a coefficient multiplied by x raised to a power from 0 to n. In this case, the polynomial would have the form: a₀ + a₁(2) + a₂(2²) + a₃(2³) + a₄(2⁴) + a₅(2⁵), where a₀, a₁, a₂, a₃, a₄, and a₅ are the coefficients. The actual value of T5(2) would depend on the specific values of these coefficients.
Learn more about 5th degree polynomial:
https://brainly.com/question/30244190
#SPJ11
Rowniel’s garden is shown below. If he increases the length and width of each section of his garden by 2 feet, what is the area, in square feet, of Rowniel’s expanded tulip section?

Answers
Answer:
180 square ft
Step-by-step explanation:
width of roses section = 80/10 = 8. so tulips section width also = 8.
length of sunflowers section = 384/24 = 16. so tulips section length = 16.
tulips section = 8 X 16 = 128 square ft.
width is increased by 2 feet. it now is 8 + 2 = 10.
length is increased by 2 feet. it is now 16 + 2 = 18.
area of expanded tulips section = 10 X 18 = 180 square ft.
What is the slope of the line
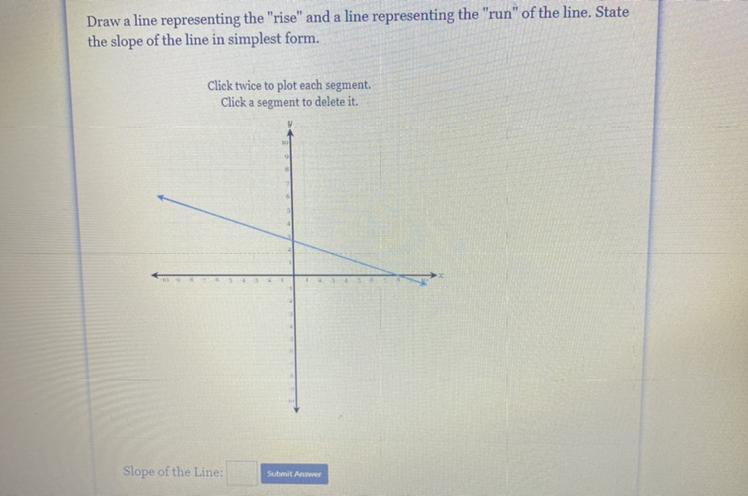
Answers
Answer:
\(\displaystyle m=\frac{-3}{8}\)
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightAlgebra I
Reading a Cartesian planeCoordinates (x, y)Slope Formula: \(\displaystyle m=\frac{y_2-y_1}{x_2-x_1}\)Step-by-step explanation:
Step 1: Define
Find points from graph.
Point (8, 0)
Point (0, 3)
Step 2: Find slope m
Simply plug in the 2 coordinates into the slope formula to find slope m
Substitute in points [Slope Formula]: \(\displaystyle m=\frac{3-0}{0-8}\)[Fraction] Subtract: \(\displaystyle m=\frac{3}{-8}\)[Fraction] Simplify: \(\displaystyle m=\frac{-3}{8}\)missing variable -3 x + 9 = -18
Answers
Answer:
x=9
Step-by-step explanation:
Plug it in. -3(9)+9=-18
Hope this helps. Plz give brainliest.
Answer:
1. Subtract 9 from both sides
-3x = -27
2. Divide by -3 on both sides
x = 9
FINAL ANSWER x = 9
What are the coefficient terms and Constants of 10x + 5 + 3x + 1
Answers
Answer:
The Coefficients in this expression are 10 and 3, while the constants are 5 and 1.
Step-by-step explanation:
Coefficients = The number that is in front of the variable.
Constant = Any number without a variable.
(Variables are the letters that you may find in an equation or function.)
Hope this helps you :)
Answer:
The coefficient are 10 and 3
The constants are 5 and 1
Step-by-step explanation:
A coefficient is the number in front of any known term.
A constant is a number by itself.
So the coefficient are 10 and 3
The constants are 5 and 1
Find sin3A, cos
3A and tan 3A when sin=1/2
Answers
Answer:
Sin 3A = 1
cos 3A = 0
tan 3 A = undefined
Step-by-step explanation:
\(\sin A = \frac{1}{2} \\ \therefore \: \sin A = \sin \: 30 \degree.. \bigg( \because \: \sin \: 30 \degree = \frac{1}{2} \bigg) \\ \therefore \: A = 30 \degree \\ \\ now \\ \sin 3A =\sin (3 \times 30 \degree)= \sin \: 90 \degree = 1 \\ \\ \cos 3A =\cos (3 \times 30 \degree)= \cos \: 90 \degree = 0\\\\ \tan 3A =\tan (3 \times 30 \degree)= \tan \: 90 \degree = \infty \)
3. Sketch the graph of the function \( y=2 \csc \left(2 x-\frac{\pi}{2}\right) \) over one period. Please label at least 2 key points and show and label any vertical asymptotes on your graph. Show your garph
Answers
The given function is[text]\(y = 2 \csc \left({2x - \frac {\pi }{2}} \right) \)[/tax]. We can express it in the form\(y = \frac{2}{\sin \left ({2x - \frac {\pi}{2}} \right)} \). Let’s sketch the graph of
y = sin x
first. We know that the graph of
y = a sin bx
is obtained from the graph of
y = sin x
by stretching the graph of
y = sin x horizontally by a factor of \(\frac{1}{b} \).
The graph of
y = 2 sin x
will be obtained by stretching the graph of
y = sin x
vertically by a factor of 2 and will pass through the origin.
x = 7π/4,
the function is –1. So, the graph looks like: Answer: The graph of the function y = 2 csc (2x – π/2) over one period is shown below.
The two vertical asymptotes are labeled. The maximum value of the function is 1 and the minimum value of the function is –1. The function is undefined at the vertical asymptotes and the zeros of the denominator. At the key points, the function is labeled with its value.
To know more about maximum visit:
https://brainly.com/question/30693656
#SPJ11