Your neighbor asks you to cut her grass. Her yard is (x +2) feet wide and (x +10) feet long. A section of the yard has a rectangular barn. The area of the barn is x^2+3x+2. What is the area of the yard that you will mow?
please help.

Answers
Related Questions
given triangle abc, how many possible triangles can be formed for the following conditions: ab = 37cm, ac = 26cm, angle b = 32.5°
Answers
Given the lengths of the two sides and the angle between them, only one triangle can be created under the given circumstances.
1. Given that angle B is 32.5°, side AB is 37 cm, side AC is 26 cm, etc.
2. Calculate side BC using the Law of Cosines:
BC = (2(AB)(AC)cosB) + (AB)(AC)2
3. Input the values that are known: BC = (37 2 + 26 2 - 2(37)(26)cos32.5°)
4. Condense: BC = (1369 plus 676 minus 1848 cos 32.5 °)
5. Determine BC =. (2095 - 1539.07)
6. Condense: BC = 556.93
7. Determine BC as 23.701 cm.
8. Since the lengths of the two sides and the angle between them are specified, only one triangle can be formed under the current circumstances.
By applying the Law of Cosines, we can determine the length of the third side, BC, given that side AB is 37 cm, side AC is 26 cm, and angle B is 32.5°. In order to perform this, we must first determine the cosine of angle B, which comes out to be 32.5°. Then, we enter this value, together with the lengths of AB and AC, into the Law of Cosines equation to obtain BC.BC = (AB2 + AC2 - 2(AB)(AC)cosB) is the equation. BC is then calculated by plugging in the known variables to obtain (37 + 26 - 2(37)(26)cos32.5°). By condensing this formula, we arrive at BC = (1369 + 676 - 1848cos32.5°). Then, we calculate BC as BC = (2095 - 1539.07), and finally, we simplify to obtain BC = 556.93. Finally, we determine that BC is 23.701 cm. Given the lengths of the two sides and the angle between them.
Learn more about triangle here
https://brainly.com/question/2773823
#SPJ4
The width of this rectangle is of the length. Find the
length and the width of the rectangle.
(2y + 6) in.
(y – 4) in.
Show your work
I WILL GIVE BRAINLIEST

Answers
Answer:
l=6, w=2
Step-by-step explanation:
Width = one-third of the length, so length = 3*width
length = 2y+6, width = y-4
l=3w, so 2y-6=3(y-4) or
2y-6=3y-12, add 12 to both sides, subtract 2y from both sides
6=y
l=2y-6 = 2(6)-6=6
w=y-4 = (6)-4 = 2
How do I factor this problem?

Answers
Answer:
\(7x(4x-1)\)
Step-by-step explanation:
First, find the largest integer that divides evenly into both numbers. In this case, 28 and 7 are both divisible by 7.
Next, find the highest degree of the variable that divides evenly into both. Here, that's just x. I'll show another example of that below.
Multiply those together, and you get 7x. That is what we need to factor out. Divide by that factor while multiplying by that factor at the same time to keep the value of the expression equal:
\(28x^2-7x\\\\7x(\frac{28x^2}{7x}-\frac{7x}{7x})\\\\7x(4x-1)\)
Another example of what I said above would be this:
Take 4x + 2. The largest integer that divides these is 2, and the highest degree of x that divides them is 0. That is an x⁰, and that is equal to 1. Multiply those, and you just get 2.
\(4x+2\\\\2(\frac{4x}{2}+\frac{2}{2})\\\\2(2x+1)\)
I'm having trouble with inequalities, any help will be appreciated, thanks.

Answers
Answer:
-3/2 ≤ x < 5
Decimal form:
-1.5 ≤ x < 5
(hope this helps)
Compare the functions shown below: f(x) = (x + 3)2 − 2 g(x) linear graph with y intercept of negative 3 over 2 and x intercept of 3 h(x) x y −3 2 −2 7 −1 14 0 23 1 34 2 47 3 62 What is the correct order of the functions from least to greatest according to the average rate of change on the interval from x = −1 to x = 3?
Answers
Answer:
For f (x):
f (x) = (x + 3) ^ 2 - 2
For x = -1
f (-1) = (-1 + 3) ^ 2 - 2
f (-1) = (2) ^ 2 - 2
f (-1) = 4 - 2
f (-1) = 2
For x = 3
f (3) = (3 + 3) ^ 2 - 2
f (3) = (6) ^ 2 - 2
f (3) = 36 - 2
f (3) = 34
AVR = ((34) - (2)) / ((3) - (- 1))
AVR = 8
For g (x):
linear graph with and intercept of negative 3 over 2 and x intercept of 3
y = mx + b
b = -3/2
For me we have:
0 = m (3) - 3/2
3m = 3/2
m = 1/2
The function g (x) is:
g (x) = (1/2) x - 3/2
For x = -1
g (-1) = (1/2) (- 1) - 3/2
g (-1) = -1/2 - 3/2
g (-1) = -4/2
g (-1) = -2
For x = 3
g (3) = (1/2) (3) - 3/2
g (3) = 3/2 - 3/2
g (3) = 0
AVR = ((0) - (- 2)) / ((3) - (- 1))
AVR = 1/2
For h (x):
Using the table we have:
AVR = ((62) - (14)) / ((3) - (- 1))
AVR = 12
Step-by-step explanation:
Answer:
from least to greatest:
1) g (x)
2) f (x)
3) h (x)
Step-by-step explanation:
please help! i can never understand these problems

Answers
Answer:
1234567891011121314151617181920
What is the area of triangle ABC?

Answers
two angles in the triangle are 60°, so the last one must be 60°, since all must add up to 180°, that means the triangle is equilateral
\(\textit{area of an equilateral triangle}\\\\ A=\cfrac{s^2\sqrt{3}}{4} ~~ \begin{cases} s=side\\[-0.5em] \hrulefill\\ s=12 \end{cases}\implies A=\cfrac{12^2\sqrt{3}}{4}\implies A=36\sqrt{3}~ ~~ units^2\)
Answer:
C.
Step-by-step explanation:
It is an equilateral triangle.
DB = 6, AB = 12, DC = height
\(DC=\sqrt{(CB)^{2}- (DB)^{2} } =\sqrt{144-36} =\sqrt{108}=\sqrt{(36)(3)} =6\sqrt{3}\)
\(A=\frac{(DC)(AC)}{2} =\frac{(6\sqrt{3})(12) }{2} =\frac{72\sqrt{3} }{2} =36\sqrt{3}\)
Hope this helps
Find the area of the shaded region

Answers
Answer:
40.5
Step-by-step explanation:
Area of square is 9x9=81.
Area of triangle is 1/2(9)(9)=40.5
81-40.5=40.5
40.5 is the area of the shaded region.
Make an exponential equation that is equal to x = 8
Answers
An exponential equation that is equal to x = 8 can be expressed as 2^3 = 8.
In an exponential equation, the base raised to the exponent equals the value of x. To create an exponential equation equal to x = 8, we need to determine the base and exponent.
In this case, the base is 2, and the exponent is 3. When we raise 2 to the power of 3 (2^3), we get 8. Therefore, the exponential equation 2^3 = 8 is equivalent to x = 8.
In the equation 2^3 = 8, the base 2 represents the factor by which x is being multiplied, and the exponent 3 represents the number of times the base is multiplied by itself. When we evaluate this equation, we find that 2^3 equals 8, which satisfies the condition x = 8.
To learn more about exponential equation click here: brainly.com/question/29506679
#SPJ11
Including 8% sales tax, an inn charges $162 per night. Find
the inn's nightly cost before the tax is added.
Answers
Answer:
$150
Step-by-step explanation:
x + 0.08x = 162
1.08 x = 162
x = 150
The inn's nightly cost before the tax is added is $150.
Let's denote the inn's nightly cost before tax as "x." We are given that the inn charges $162 per night, including an 8% sales tax. This can be represented as an equation:
Total cost = Nightly cost before tax + Sales tax
$162 = x + 0.08x
Now, we can solve for "x":
$162 = 1.08x
x = $162 / 1.08
x = $150
So, the inn's nightly cost before the tax is added is $150.
We're asked to find the inn's nightly cost before the tax is added. Let's denote this cost as "x."
We are given that the total cost, including the 8% sales tax, is $162 per night. We can set up an equation using this information:
Total cost = Nightly cost before tax + Sales tax
Mathematically, this can be expressed as:
$162 = x + 0.08x
The 0.08x represents the 8% sales tax, which is 8% of the nightly cost before tax.
Now, we can combine the x terms on the right side of the equation:
$162 = 1.08x
To solve for x, we need to isolate it on one side of the equation. We can do this by dividing both sides of the equation by 1.08:
x = $162 / 1.08
x = $150
So, the inn's nightly cost before the tax is added is $150. This means that if there were no sales tax, the inn would charge $150 per night. The 8% sales tax is then added to this base cost to reach the total of $162.
To know more about Tax here
https://brainly.com/question/33580914
#SPJ3
find the value of x 40,2x,140
Answers
Answer:
set it up as equation
Step-by-step explanation:
hope this helps you get started
Write a quadratic function with zeroes 0 and – 7. Write your answer using the variable x and in standard form with a leading coefficient of 1.
Answers
This is the standard form of a quadratic function with leading coefficient 1, and 0 and -7.
If the zeros of a quadratic function are 0 and -7, then the function can be written as:
f(x) = a(x - 0)(x - (-7))
Simplifying:
f(x) = a(x)(x + 7)
To find the value of 'a', we can use one of the points on the parabola. Since we know that the x-intercept is 0, we can substitute x = 0 and y = 0 into the equation:
0 = a(0)(0 + 7)
0 = 0
This tells us that a can be any value, as long as it's not 0. Let's choose a = 1 for simplicity. Then the quadratic function with zeros 0 and -7 is:
f(x) = (x)(x + 7)
f(x) = x^2 + 7x
To learn more about quadratic :
https://brainly.com/question/21145944
#SPJ1
find the missing side length in the right triangle.
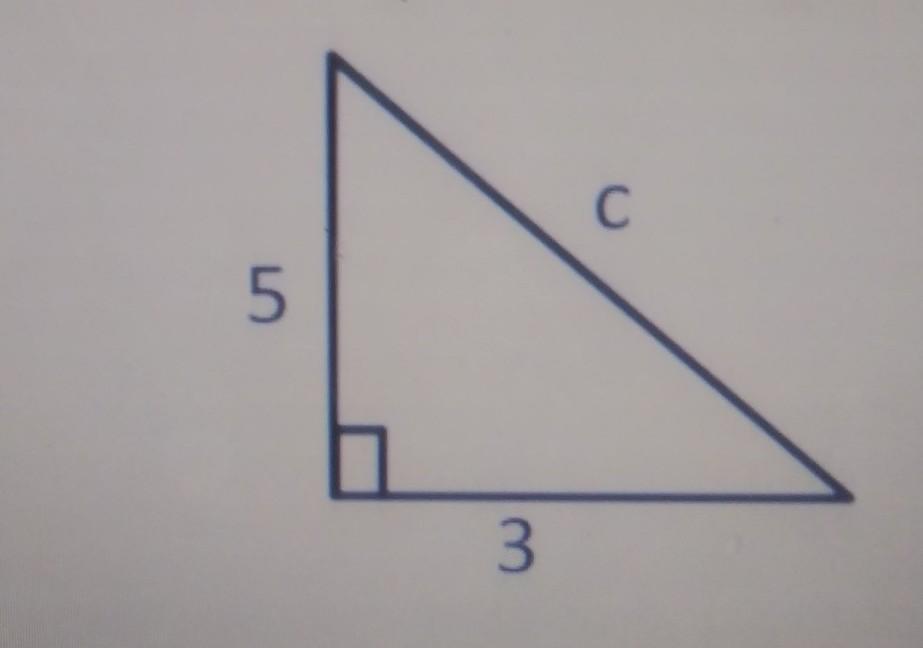
Answers
Answer:
5.83
Step-by-step explanation:
Pythagorean Theorem a^2 + b^2 = c^2
\(5^{2} + 3^{2} = 34\\\sqrt{34} = 5.83\)
A quantity with an initial value of 7800 decays continuously at a rate of 0. 1%
per hour. What is the value of the quantity after 1. 25 days, to the nearest
hundredth?
Answers
The question is asking for the value of a quantity that decays continuously at a rate of 0.1% per hour. We are given that the initial value of the quantity is 7800 and are asked to find the value after 1.25 days (30 hours).
What is a ratio in mathematics?
A ratio in mathematics demonstrates how many times one number is present in another. For instance, if a dish of fruit contains eight oranges and six lemons, the ratio of oranges to lemons is eight to six (that is, 8:6, which is equivalent to the ratio 4:3).
We can use the following formula to find the final value of the quantity after a certain amount of time:
final value = initial value * (1 - decay rate)^time
Where decay rate is given as a decimal (0.1% = 0.001)
Plugging in the given values, we get:
final value = 7800 * (1 - 0.001)^30
The final value is around 7396.65
Rounding the final value to the nearest hundredth, the final value after 1.25 days is:
7396.65 ≈ 7396.66
The value of the quantity after 1.25 days, to the nearest hundredth is 7396.66.
Learn more about ratio
https://brainly.com/question/12024093
#SPJ4
Based on the graphs of the equations y = x + 7 and y = x2 – 3x + 7, the solutions are located at points:
Answers
The correct option is A. (4, 11) and (0, 7).
The solution of the equations y = x + 7 and y = x² – 3x + 7, the solutions are located at points: (4, 11) and (0, 7).
What is the system of linear equation?Estimate the y-intercept, slope, and express the equation in the form of the y-intercept (y = mx + b) to find the graphed equation. The slope is the difference between the y- and x-axis values.
A graph equation is an equation in graph theory where the unknown is a graph. Isomorphic ideas are one of the key issues in graph theory.
The equations are; y = x + 7 and y = x² - 3x + 7
At the solution, the u-values are equal, which gives;
y = y
x + 7 = x² - 3·x + 7
x² - 3·x + 7 - (x + 7) = 0
x² - 4·x = 0
x·(x - 4) = 0
x = 4, or x = 0
When x = 4, y = 4 + 7 = 11
When x = 0,
y = 0 + 7 = 7
Therefore, the solution for the equations y = x + 7 and y = x² - 3x + 7 are are located at points: (4, 11) and (0, 7).
To know more about system of linear equations, here
https://brainly.com/question/14323743
#SPJ4
The complete question is-
Based on the graphs of the equations y = x + 7 and y = x² – 3x + 7, the solutions are located at points:
A. (4, 11) and (0, 7)
B. (4, 11) and (–7, 0)
C. (–7, 0) and (1.5, 4.75)
D. (1.5, 4.75) and (0, 7)
Develop an essenential smoothing forecast (α=0.45) for penods 11 through 15 Assume that your forecast for penod 10 was 297 Calculate the forecasts for perieds 11 through 15 (enter your responses rocmdod to tivo decimal places)
Answers
The forecasts for periods 11 through 15 are: F11 = 297.4, F12 = 296.7, F13 = 297.1, F14 = 296.9, F15 = 297.0
Given: Smoothing constant α = 0.45, Forecast for period 10 = 297
We need to calculate the forecasts for periods 11 through 15 using the essential smoothing forecast method.
The essential smoothing forecast is given by:Ft+1 = αAt + (1 - α)
Ft
Where,
At is the actual value for period t, and Ft is the forecasted value for period t.
We have the forecast for period 10, so we can start by calculating the forecast for period 11:F11 = 0.45(297) + (1 - 0.45)F10 = 162.35 + 0.45F10
F11 = 162.35 + 0.45(297) = 297.4
For period 12:F12 = 0.45(At) + (1 - 0.45)F11F12 = 0.45(297.4) + 0.55(297) = 296.7
For period 13:F13 = 0.45(At) + (1 - 0.45)F12F13 = 0.45(296.7) + 0.55(297.4) = 297.1
For period 14:F14 = 0.45(At) + (1 - 0.45)F13F14 = 0.45(297.1) + 0.55(296.7) = 296.9
For period 15:F15 = 0.45(At) + (1 - 0.45)F14F15 = 0.45(296.9) + 0.55(297.1) = 297.0
Therefore, the forecasts for periods 11 through 15 are: F11 = 297.4, F12 = 296.7, F13 = 297.1, F14 = 296.9, F15 = 297.0 (All values rounded to two decimal places)
Know more about Smoothing constant:
https://brainly.com/question/32292658
#SPJ11
Evaluate x−y if x=−5 1/4 and y=−6.8 . Write your answer in simplest form.
Answers
The answer i got is -1.55, im not sure though
The value of the given algebric expression is x - y when x=−5 1/4 and y=−6.8 will be 2.05.
What is an expression?A mixture of variables, numbers, addition, subtraction, multiplication, and division are called expressions.
An expression is a mathematical proof of the equality of two mathematical expressions.
As per the given expression, x - y
x = - 5 1/4 = (-5 x 4 + 1)/4 = -19/4 = -4.75
y = -6.8
Substitute x and y into the above expression,
-4.75 - (-6.8) = 2.05
Hence "The value of the given algebric expression is x - y when x=−5 1/4 and y=−6.8 will be 2.05".
To learn more about expression,
https://brainly.com/question/14083225
#SPJ2
Find the equation of the line.
Use exact numbers.
y = __x+__

Answers
HELP ME WITH THESE PLEASE AND SHOW ALL YOUR WORK

Answers
Answer:
12. x = \(\sqrt{7}\)
15. x = \(\sqrt{330}\)
Step-by-step explanation:
12. 7\(x^{2}\) = 49
\(\frac{7x^2}{7}\)= \(\frac{49}{7}\)
\(x^{2}\) = 7
\(\sqrt{x^2}\) = \(\sqrt{7}\)
x = \(\sqrt{7}\)
15. \(\frac{x^2}{3\\}\)=110
3* \(\frac{x^2}{3}\) = 110*3
\(x^{2}\) = 330
\(\sqrt{x^2}\) = \(\sqrt{330}\)
x = \(\sqrt{330}\)
RIGHT OR WRONG PLZZZZZZZZZZZZZZZZZZ HELPPPPPPPPPPPPP

Answers
Answer:i dunno
Step-by-step explanation:
WRONG
How can you investigate chance processes and evelop, use, and evaluate probability models?
Answers
Investigating chance processes and developing, using, and evaluating probability models involves understanding and analyzing the concepts of probability.
Conducting experiments or simulations, and interpreting the results. Here are the key steps involved in investigating chance processes and developing probability models:
Define the problem: Clearly articulate the question or situation that involves uncertainty and randomness. This could be related to real-world scenarios or hypothetical situations.
Identify the sample space: Determine all the possible outcomes of the chance process. The sample space is the set of all these outcomes.
Assign probabilities: Assign probabilities to each outcome or set of outcomes in the sample space. This step requires considering the characteristics of the situation and using mathematical reasoning, historical data, or experimental results to estimate the likelihood of each outcome.
Build probability models: Probability models can take different forms depending on the situation. For simple scenarios, you can use theoretical models such as the classical, empirical, or subjective approaches. For more complex situations, you may need to develop mathematical models or use simulation techniques.
Conduct experiments or simulations: Perform experiments or simulations to gather data and observe the outcomes. This can involve conducting physical experiments, running computer simulations, or using other methods to generate random outcomes.
Analyze the results: Analyze the collected data to assess the frequency of different outcomes and compare them with the predicted probabilities from the probability model. This helps in evaluating the accuracy and validity of the model.
Refine the model: If the observed results significantly differ from the predicted probabilities, revise the probability model to better represent the actual chance process. This may involve adjusting the assigned probabilities or considering additional factors that were initially overlooked.
Make predictions and draw conclusions: Once a probability model is developed and validated, you can use it to make predictions about future events or draw conclusions about the likelihood of specific outcomes.
Evaluate the model: Continuously evaluate the probability model based on new data or changing circumstances. Assess its performance and make adjustments if necessary.
By following these steps, you can investigate chance processes, develop probability models, and gain insights into the uncertainty and randomness associated with various situations. Probability models help in quantifying and understanding the likelihood of different outcomes, enabling better decision-making and risk assessment in a wide range of fields such as statistics, finance, engineering, and social sciences.
Learn more about probability at: brainly.com/question/32117953
#SPJ11
A rectangle with an area of 54 square units is on a coordinate plane. One point is located at (5,9) and two other points are located on the x axis. What is the perimeter of the rectangle?
Answers
The perimeter of the rectangle is 2(sqrt(82) + 4) units.
what is perimeter?
Perimeter is the total distance around the outside of a two-dimensional shape. It is the sum of the lengths of all the sides of the shape. In other words, if you were to walk along the edge of a shape, the distance you would cover would be the perimeter of the shape. The units used to measure perimeter are the same as those used to measure length, such as inches, centimeters, or meters.
Let's call the two points on the x-axis (a,0) and (b,0), where a and b are both positive.
Since the rectangle has an area of 54 square units, we know that:
length x width = 54
We also know that one point is located at (5,9), so the length of the rectangle must be the distance between (5,9) and (a,0) or (b,0). Similarly, the width must be the distance between (5,9) and (a,0) or (b,0).
Let's first find the length. The distance formula gives us:
length = sqrt((5-a)^2 + 9^2) or sqrt((5-b)^2 + 9^2)
Next, let's find the width. Again, using the distance formula, we have:
width = sqrt((a-b)^2 + 0^2)
Now we can use the fact that the area of the rectangle is 54 to solve for a and b.
54 = length x width
54 = sqrt((5-a)^2 + 9^2) x sqrt((a-b)^2 + 0^2)
54 = sqrt((5-a)^2 x (a-b)^2 + 0^2)
2916 = (5-a)^2 x (a-b)^2
Since a and b are both positive, we know that 5 > a > b. Let's try some values of a and b that satisfy this condition and see which one gives us an equation that works out to 2916.
If a = 4 and b = 2, we get:
2916 = (5-4)^2 x (4-2)^2 = 4
This doesn't work. Let's try a = 3 and b = 2:
2916 = (5-3)^2 x (3-2)^2 = 4
Still doesn't work. Let's try a = 6 and b = 2:
2916 = (5-6)^2 x (6-2)^2 = 16
This works! So the two points on the x-axis are (2,0) and (6,0).
Now we can find the length and width:
length = sqrt((5-6)^2 + 9^2) = sqrt(82)
width = sqrt((6-2)^2 + 0^2) = 4
Finally, we can find the perimeter:
perimeter = 2 x length + 2 x width
perimeter = 2 x sqrt(82) + 2 x 4
perimeter = 2(sqrt(82) + 4)
Therefore, the perimeter of the rectangle is 2(sqrt(82) + 4) units.
To learn more about perimeter from the given link
https://brainly.com/question/6465134
#SPJ9
Which equation below models this situation? Last week, Tina worked 36 hours in 6 days. She worked the same number of hours each day. How many hours did she work each day?
6h = 36
h/6 = 36
h - 6 = 3
h + 6 = 36
Answers
Answer:
6h = 36
Step-by-step explanation:
h is for the number of hours she worked each day. She worked in 6 days for 36 hours so 6h = 36.
what is a linear equation that contains these points?

Answers
Answer:
C
Step-by-step explanation:
If you plug in the numbers into that equation you get
1 = -2(2) + 5
1 = -4 + 5
1 = 1
You can also do this again with x = 5 y = -5
-5 = -2(5) + 5
-5 = -10 + 5
-5 = -5
How do you identify an exponential graph?
Answers
Exponential graph is identified by its curve.
An exponential graph is a graph that shows a rapid increase or decrease of a value over time, where the rate of change is proportional to the current value. It is usually represented by a curve that bends upward or downward.
The key characteristic of an exponential graph is that the Y-axis is on a logarithmic scale, and the curve of the graph is a steep curve going either up or down. The equation of an exponential graph is usually of the form y = ab^x, where a is the initial value, b is the growth or decay factor, and x is the independent variable.
To more about Exponential graphs visit: brainly.com/question/9834848
#SPJ4
Point E is the midpoint of AB and point F is the midpoint of CD .
Which statements about the figure must be true? Check all that apply.
AB is bisected by . CD
CD is bisected by . AB
AE = 1/2 AB
EF = 1/2 ED
FD= EB
CE + EF = FD
Answers
The statements that must be true about the figure are
AB is bisected by EF,CD is bisected by AB, AE = 1/2 AB, EF = 1/2 ED,
FD = EB.
AB is bisected by EF: This statement is true because point E is the midpoint of AB, meaning it divides AB into two equal parts, and EF is a line connecting the midpoints of the sides. Therefore, EF bisects AB.
CD is bisected by AB: This statement is also true because point F is the midpoint of CD, meaning it divides CD into two equal parts, and AB is a line connecting the midpoints of the sides. Therefore, AB bisects CD.
AE = 1/2 AB: This statement is true because E is the midpoint of AB, which means AE and EB are equal in length. Since E is the midpoint, AE is half the length of AB.
EF = 1/2 ED: This statement is true because F is the midpoint of CD, and EF is a line connecting the midpoints of the sides. Therefore, EF is half the length of CD, and ED is twice the length of EF.
FD = EB: This statement is true because F is the midpoint of CD, meaning FD and EB are equal in length.
Learn more about midpoint and bisector: brainly.com/question/10028387
#SPJ11
ayeeeee dis one jsjkskksnns lol

Answers
Answer:
thanks for the points
Step-by-step explanation:
Answer:
0
Step-by-step explanation:
Do this formula y2 - y1/x2-x1
PLUG IN (8, -9) and (14, -9)
-9 - -9/ 14 - 8
0/6
0
The slope is 0
each of two pesticide brands is applied to 100 containers of fire ants. brand1 killed all ants in 65 of 100 containers within two hours, and brand 2 killed all ants in 58 of 100 containers within two hours.
Answers
The pValue is 0.15625 > 0.05 when brand1 killed all ants in 65 of 100 containers within two hours, and brand 2 killed all ants in 58 of 100 containers within two hours in hypothesis.
Let A represent the new pesticide and B be the Ant Killer. Then, you are given that
Brand1 kills ants in 65 of 100 containers:
Xa = 65/100 = 0.65
Brand2 kills ants in 58 of 100 containers:
Xb = 58/100 = 0.58
You know need to find sample variance for both,
s²A =∑(Xi - Xa)
= 65(1-0.65)² + 35(0 - 0.65)²
= 22.7
s²B =∑(Xi - Xb)²
= 59(1-0.59)² + 41(0 - 0.59)²
= 24.19
You can know do a test for significance
t = (Xa - Xb) / √(sA /nA) +(sB/nB)
and derive the conclusion from there
Here, Null and alternative hypothesis are generally,
Alternative hypothesis
Here, there are three samples are assumed. They are:
i) Samples are taken independently
ii) Samples must be selected randomly
iii) n₁p₁ ≥ 5 , n₁q₁ ≥ 5, n₂p₂ ≥ 5, n₂q₂ ≥ 5
i.e., p₁ = 0.65 ; p₂ = 0.58 , n₁= 100
q₁ = 0.35 ; q₂ = 0.42 , n₂=100
Corresponding p-value at Z = 1.01722
p-value = 0.15625 > 0.05
Hence, the pValue is 0.15625 > 0.05 when brand1 killed all ants in 65 of 100 containers within two hours, and brand 2 killed all ants in 58 of 100 containers within two hours in hypothesis.
To know more about hypothesis check the below link:
https://brainly.com/question/606806
#SPJ4
yeaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa

Answers
5. M's class is having a give-away
here 3 of her lucky students will
ceive 500 classroom credits. She
ll pull names out of a hat and select
winners. Once a student wins, they
e not eligible to win again. There
e 75 total students in the class,
cluding you and your 2 best friends.
Answers
The probability that both I and my best friend get the 100 classroom credits is 0.06%.
What is probability?Probability is defined as the ratio of the number of favourable outcomes to the total number of outcomes in other words the probability is the number that shows the happening of the event.
Since Mr Q's class is having a give-away where his students can receive 100 classroom credits, he will pull names out of a hat and select two winners, and once a student wins, they are not eligible to win a second time, if there are 40 total people in the class, including me and my best friend, to determine what is the probability that both I and my best friend get the 100 classroom credits, the following calculation must be performed:
I = 1/40 = 0.025
my best friend = 1/39 = 0.02564
0.02564 x 0.025 = X
0.0006410 = X
X x 100 = 0.064
Therefore, the probability that both I and my best friends get the 100 classroom credits is 0.06%.
To know more about probability follow
https://brainly.com/question/24756209
#SPJ1