5. 6.9Write the decimal as a a fraction or mixed number?
Answers
6.9 as a fraction or mixed number
6.9 = 6 9/10
This is also the same as 69/10
Related Questions
What is the equation of a line that is perpendicular to 2x + y = -4 and passes through the point (2, -8)?
Enter your answer as a slope intercept equation (y=mx+b) in the box.
Answers
Answer:
y = 1/2 x - 9
Step-by-step explanation:
y = -2x - 4
slope of a perpendicular line = 1/2
y -(-8) = 1/2 (x-2)
y + 8 = 1/2 x - 1
y = 1/2 x - 1 - 8
y = 1/2 x - 9
STAINED GLASS Pablo made the stained glass
window shown. He used an inscribed square and
equilateral triangle for the design.
a. Label the angle measures on the outer edge of the
triangle.
b. Label all of the arcs with their degree measure.

Answers
a) The angles outside the side PQ measure 65° and 25°
The angles outside the side QR measure 85° and 95°
The angles outside the side PR measure 55° and 35°
b) The arc PR, PQ and PR measure 120°
a)
Let us assume that the inscribed square be ABCD and equilateral triangle is PQR.
Let side PR of triangle intersects the quadrilateral at points M and N.
So, we get a triangle DMN outside the equilateral triangle.
Here, ∠DMN = 55°, ∠D = 90°
So, ∠MND = 180 - (90 + 55)
= 35°
Similarly, side PQ of triangle PQR intersects the quadrilateral at points X and Y.
So, we get a triangle AXY outside the equilateral triangle.
From triangle PXM we get the measure of angle PXM which is 65 degrees.
As angle PXM and angle AXY are opposite angles, the measure of angle AXY = 65°
∠A = 90°
So, ∠AYX = 180° - (∠A + ∠AXY )
= 180° - (90° + 65°)
= 25°
Let the side QR of triangle PQR intersects the quadrilateral at points L and K.
so we get new quadrilateral LKBC
In this quadrilateral ∠B = 90°, ∠C = 90°
From triangle QYL, we get the measure of angle QLY = 95°
So, the measure of ∠KLB = 95° .......(∠QLY and ∠KLB opposite angles)
So, the remaining angle LKC of quadrilateral LKBC would be,
∠LKC = 360° - (∠B + ∠C + ∠KLB)
∠LKC = 360° - (90 °+ 90° + 95°)
∠LKC = 85°
b)
We know that he angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.
so, the measure of arc PR = 120°
the measure of arc PQ = 120°
the measure of arc RQ = 120°
Learn more about the triangle here:
https://brainly.com/question/14965331
#SPJ1

1. Identify the plane parallel to plane ACE
Answers
Answer:
It has parallel sides
Step-by-step explanation:
Sam and two friends put letters in envelopes on Monday.
The three of them take two hours to put 600 letters in envelopes.
On Tuesday Sam has three friends helping.
Working at the same rate, how many letters should the four of them be able to put in
envelopes in two hours?
Answers
Answer: 800 envelopes
Step-by-step explanation:
Sam and her friends are working at a rate of 100 letters in envelopes per hour per person. So, if there are 4 people helping including sam, you just have to multiply 400 by 2 hours, which will give you 800.
Prove that the set of functions from N to N is uncountable, by using a diagonalization argument. N is the set of natural numbers.
Answers
Hence Proved N to N is uncountable set by using a diagonalization argument
What is Diagonalization Argument?
Georg Cantor published the Cantor's diagonal argument in 1891 as a mathematical demonstration that there are infinite sets that cannot be put into one-to-one correspondence with the infinite set of natural numbers. It is also known as the diagonalization argument, the diagonal slash argument, the anti-diagonal argument, the diagonal method, and Cantor's diagonalization proof.
Proof:
We write f as the sequence of value it generates
that is, say f:N-N is defined as f(x) =x then
we write f as : 1,2,3,4........
similarly if f:N-N were f(x) = 2x then we write it as :2,4,6,8.......
now assume on the contrary that the set of functions from N to N is countable
then,
\(f_{1}\) : \(f_{11}\) \(f_{12}\) \(f_{13}\) , ...........
\(f_{2}\) : \(f_{21}\) \(f_{22}\) \(f_{23}\) , ...........
\(f_{3}\) : \(f_{31}\) \(f_{32}\) \(f_{33}\) , ........... and so on
Here \(f_{ij}\) =\(f_{i}(j)\)
consider the function f as :
f : (\({f11}\) +1 ) , (\({f22}\) +1) , (\({f33}\) +1),.........
Then f wouldn't appear in the list of the function we had above since any \(f_{i}\) would disagree with f at the i th place
Therefore the set of the function from N to N is an uncountable set
To learn more about diagonalization argument visit:
brainly.com/question/16991671
#SPJ4
What is the slope of the line that contains the points (8, 4) and (−4, 8)?
3
−3
one third
negative one third
Answers
Answer: negative one third
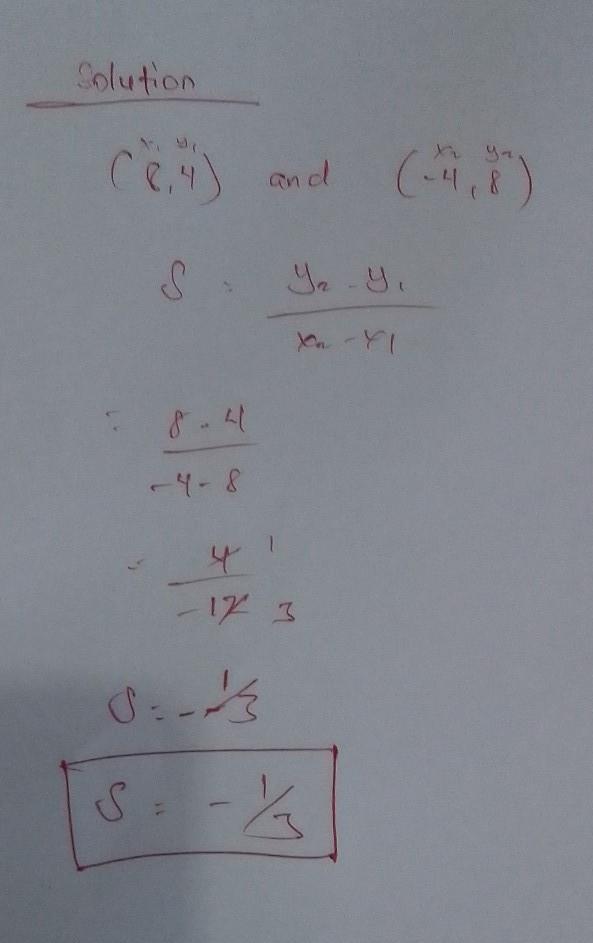
Answer:
-1/3
Explanation:
There's a formula that I'll use to find the slope - it's called the slope formula.
\(\sf{m=\dfrac{y_2-y_1}{x_2-x_1}}\)
Plug in the data:
\(\sf{m=\dfrac{8-4}{-4-8}}\\\\\sf{m=\dfrac{4}{-12}\)
Simplify:
\(\sf{m=-\dfrac{4}{12}}\)
\(\sf{m=-\dfrac{1}{3}}\)
Hence, the slope is negative one-third.
Find the critical value needed to construct a confidence interval of the given level with the given sample size. Round the answers to three decimal places.
Part 1 of 4
(a) For level 95% and sample size 7.
Part 2 of 4
(b) For level 98% and sample size 12.
Part 3 of 4
(c) For level 99% and sample size 27.
Part 4 of 4
(d) For level 98% and sample size 14.
Answers
Answer:
a) \( t_{\alpha/2}=\pm 2.447\)
b) \( t_{\alpha/2}=\pm 2.718\)
c) \( t_{\alpha/2}=\pm 2.779\)
d) \( t_{\alpha/2}=\pm 2.650\)
Step-by-step explanation:
Part a
The degrees of freedom are given by:
\( df=n-1= 7-1=6\)
The confidence is 95% or 0.95 the significance would be \(\alpha=0.05\) and the critical values would be:
\( t_{\alpha/2}=\pm 2.447\)
Part b
The degrees of freedom are given by:
\( df=n-1=12-1=11\)
The confidence is 98% or 0.98 the significance would be \(\alpha=0.02\) and the critical values would be:
\( t_{\alpha/2}=\pm 2.718\)
Part c
The degrees of freedom are given by:
\( df=n-1=27-1=26\)
The confidence is 99% or 0.99 the significance would be \(\alpha=0.01\) and the critical values would be:
\( t_{\alpha/2}=\pm 2.779\)
Part d
The degrees of freedom are given by:
\( df=n-1=14-1=13\)
The confidence is 98% or 0.98 the significance would be \(\alpha=0.02\) and the critical values would be:
\( t_{\alpha/2}=\pm 2.650\)
A value of a test statistic defines the upper bounds of a confidence interval, statistical significance in a test statistic is known as the crucial value.
critical value:For part a )
n = 7
Calculating the degrees of freedom \(= df = n - 1 = 7 - 1 = 6\)
At \(95\%\) the confidence level, the t:
\(\alpha = 1 - 95\% = 1 - 0.95 = 0.05\\\\\frac{\alpha}{ 2} = \frac{0.05}{ 2} = 0.025\\\\t_{\frac{\alpha}{ 2}}\\\\df = t_{0.025,6} = 2.447\\\\\)
The critical value = 2.447
For part b )
n =12
Calculating the degrees of freedom\(= df = n - 1 = 12 - 1 = 11\)
At \(98\%\) the confidence level , the t:
\(\alpha = 1 - 98\% = 1 - 0.98 = 0.02\\\\\frac{\alpha}{ 2}= \frac{0.02}{ 2} = 0.01\\\\t_{\frac{\alpha}{ 2}}\\\\df = t_{0.01,11} =2.718\\\\\)
The critical value =2.718
For part c )
n = 27
Calculating the degrees of freedom \(= df = n - 1 = 27 - 1 = 26\)
At \(99\%\) the confidence level, the t:
\(\alpha = 1 - 99\% = 1 - 0.99 = 0.01\\\\\frac{\alpha}{ 2} = \frac{0.01}{ 2} = 0.005\\\\t_{\frac{\alpha}{ 2}}\\\\df = t_{0.005,26}=2.779\\\\\)
The critical value =2.779
For part d )
n = 14
Calculating the degrees of freedom \(= df = n - 1 = 14 - 1 = 13\)
At \(98\%\) the confidence level, the t:
\(\alpha = 1 - 98\% = 1 - 0.98 = 0.02\\\\\frac{\alpha}{ 2} = \frac{0.02}{ 2} = 0.01\\\\t_{\frac{\alpha}{ 2}} \\\\df = t_{0.01,13} =2.650\)
The critical value =2.650
Find out more about the critical value here:
brainly.com/question/14508634
Determine if the equation given in slope-intercept form represents the graph. If the equation is correct support your reasoning with why it is correct. If the equation is incorrect, give the correct slope-intercept form equation explaining how you determined it.

Answers
The equation of the line would be y = (4/5)x + 4 which in slope-intercept form represents the graph.
The graph is given in the question.
As per the given line, we take two points (0, 4) and (5, 8)
Let the required line would be y - y₁ = (y₂ - y₁)/(x₂ -x₁ )[x -x₁]
x₁ = 0, y₁ = 4
x₂ = 5, y₂ = 8
⇒ y - y₁ = (y₂ - y₁)/(x₂ -x₁ )[x -x₁]
Substitute values in the equation, we get
⇒ y - 4 = (8 - 4)/(5-0 )[x -0]
⇒ y - 4 = (4/5)x
⇒ y = (4/5)x + 4
The given equation of the line y = 4x + 5 is incorrect because its slope is not correct.
So, the equation of the line would be y = (4/5)x + 4.
Learn more about the Slope of the Line here:
brainly.com/question/14511992
#SPJ1
Lucy runs an 80-metre race in 16 seconds.
During the first 10 seconds her speed increases at a constant rate.
During the last 6 seconds her speed increases at a different constant rate.
Her speed at 16 seconds is 2 m/s more than her speed at 10 seconds.
a) Work out her acceleration during
the last 6 seconds.
State the units of your answer.
b) When Lucy finishes the 80-metre race,
her speed is v m/s
Work out the value of v.
Answers
a)Lucy's acceleration during the last 6 seconds is 1/3 m/s².
b) Lucy's speed at the end of the 80-meter race is 6.67 m/s.
Define accelerationAcceleration is a physical quantity that measures the rate at which the velocity of an object changes with time. It is defined as the rate of change of velocity (v) with respect to time (t), and is usually denoted by the symbol "a".
a) Let's assume that Lucy's speed increases at a constant rate "a" during the last 6 seconds. Then we can use the following kinematic equation to find her speed at 16 seconds:
v = u + at
where "v" is her final speed at 16 seconds,
"u" is her initial speed at 10 seconds,
"a" is her acceleration during the last 6 seconds,
and "t" is the time interval of 6 seconds.
v = u + 2
Substituting these values into the equation above, we get:
u + 2 = u + 6a
Simplifying and solving for "a", we get:
a = 1/3 m/s²
Therefore, Lucy's acceleration during the last 6 seconds is 1/3 m/s².
b) Let's first find Lucy's average speed during the entire 16 seconds:
average speed = total distance / total time
The total distance is 80 meters and the total time is 16 seconds, so:
average speed = 80 / 16 = 5 m/s
Now, we can use the following kinematic equation to find Lucy's final speed "v":
v² = u² + 2as
where "u" is her initial speed at 0 seconds,
"a" is her average acceleration during the entire 16 seconds,
"s" is the total distance of 80 meters,
and "v" is her final speed at 16 seconds.
We can rearrange this equation to solve for "v":
v = √(u²+ 2as)
her speed at 10 seconds is:
u = at = (a)(10) = 10a
Substituting these values into the equation above, we get:
v = √((10a)² + 2a(80))
Simplifying and substituting the value of "a" that we found in part a), we get:
v = 6.67 m/s
Therefore, Lucy's speed at the end of the 80-meter race is 6.67 m/s.
To know more about velocity, visit;
https://brainly.com/question/17127206
#SPJ1
Determine whether y varies directly with x
y = 6x
true
false
HELP!!!
Answers
Answer:
true
Step-by-step explanation:
i believe its true, i may be wrong, if so, im sorry :((
Find the length of the unknown side in the right triangle.

Answers
Answer:
here
let ABC is triangle
SO

2x-1=y
3x-1=y
Consider the system of equations above. Which of the following statements about this system is true?

Answers
Answer:
B; There is only one (x,y) solution and y is negative
Step-by-step explanation:
First, I graphed the two equations. Attached is an image of the equations graphed. Next, I looked for overlapping points. Wherever the two points overlap, there is a solution. When looking at the graph, we can see the lines overlap at only one point, (0,-1). Since y is negative, the answer must be B; there is only one (x,y) solution and y is negative.
If this answer helped you, please leave a thanks!
Have a GREAT day!!!

a number less eleven algebraic
Answers
Let the variable n represent the number
\( \sf \longrightarrow \: n\)
Less eleven means subtract eleven from the variable\( \sf \longrightarrow \: n - 11\)
➪Thus, The equation is (n-11)
The diagram shows a convex polygon what is the value of s please help me
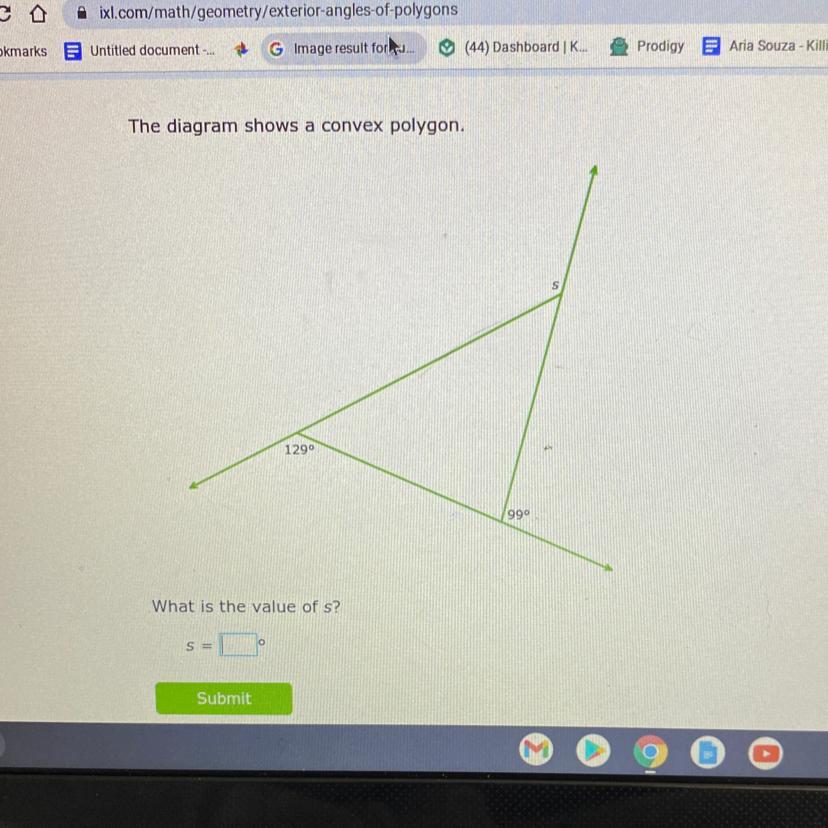
Answers
Consider a differentiable function f having domain all positive real numbers, and for which it is known that f'(x) = (4 - x)x^-3 for x > 0. (a) Find the t-coordinate of the critical point of f. Determine whether the point is a relative maximum, a relative minimum, or neither for the function f. Justify your answer. (b) Find all intervals on which the graph of f is concave down. Justify your answer. (c) Given that f(1) = 2, determine the function f.
Answers
x=4 is the t-coordinate of the f's critical point. For the function f, ascertain whether the point is a relative maximum, relative minimum, or neither.
Given that,
Consider a differentiable function f having domain all positive real numbers, and for which it is known that f'(x) = (4 - x)/x³ for x > 0
We have to find
(a)Discover the t-coordinate of the f's critical point. For the function f, ascertain whether the point is a relative maximum, relative minimum, or neither.
We know that,
f'(x) = 4-x/x³ = 4/x³ - 1/x²
Critical point f'(x)=0
4-x/x³=0⇒x=4
Therefore, x=4 is the t-coordinate of the f's critical point. For the function f, ascertain whether the point is a relative maximum, relative minimum, or neither.
To learn more about coordinates visit: https://brainly.com/question/27749090
#SPJ4
can you solve this quesiton?

Answers
Using chain rule, the derivative of the function is 1 / [4x^(3/4) (1 + x^(1/2))].
What is the derivative of the function?Let u(x) = √4. Then we can write the given function as d/dx[tan^-1(u(x))].
Recall that the chain rule for differentiation states that d/dx[f(g(x))] = f'(g(x)) * g'(x). Applying this to our function, we have:
d/dx[tan^-1(u(x))] = [d/dx(tan^-1(u))] * [d/dx(u(x))]
To find d/dx(tan^-1(u)), we use the formula for the derivative of the inverse tangent function: d/dx[tan^-1(u)] = u'(x) / [1 + u(x)^2].
To find u'(x), we differentiate u(x) = sqrt4 with respect to x using the chain rule as follows:
d/dx[√4] = (1/2)x^(-3/4) * (d/dx)(x) = (1/2)x^(-3/4)
Therefore, u'(x) = (1/2)x^(-3/4).
Substituting u(x) and u'(x) into the formula for the derivative of the inverse tangent function, we get:
d/dx[tan^-1(u(x))] = [1 / (2x^(3/4) * (1 + x))]
Finally, substituting this expression for d/dx(tan^-1(u)) and d/dx(u(x)) back into our original chain rule expression from step 2, we get:
d/dx[tan^-1(√4)] = [1 / (2x^(3/4) * (1 + x))] * (1/4)x^(-3/4)
Simplifying the expression in step 6 by multiplying the two terms in the denominator and bringing x to the common denominator, we get:
d/dx[tan^-1(√4)] = 1 / [4x^(3/4) (1 + x^(1/2))]
Therefore, the derivative of the function d/dx[tan^-1(√4)] is 1 / [4x^(3/4) (1 + x^(1/2))].
Learn more on derivative of a function here;
https://brainly.com/question/12047216
#SPJ1
ttttttttttttttttttt
q
Answers
Answer: rwar
Step-by-step explanation:
Can you please find and solve the unknown variable.

Answers
The value of x is; x = 3.14
Here, we have,
from the given diagram, we get,
there is a right angle triangle.
we have to find the value of x.
we know that,
Let the angle be θ , such that
cos θ = base / hypotenuse
here, we get,
cos 17 = 3/x
so, we have,
0.956 = 3/x
so, x = 3.14
Hence, The value of x is;x = 3.14
To learn more about trigonometric relations click :
brainly.com/question/14450671
#SPJ1
Two figures are said to be SIMILAR if they are the same shape. In more mathematical language, two figures are similar if their corresponding angles are congruent , and the ratios of the lengths of their corresponding sides are equal. This common ratio is called the scale factor.
Each pair of figures is similar. Find the value of the missing side (x). Round your answer to the nearest tenth if necessary.

Answers
Answer:
4.9 in
Step-by-step explanation:
6/11 = x/9
6/11 times 9 = x
x = 4.9
Please help! I don't know how to do slopes.

Answers
The slope of the given line in the image is -4 , Option A is the answer.
What is the equation of a straight line ?The equation of the straight line is given by
y =mx +c ,
Where m is the slope , C is the intercept
The line is passing through the point
(-1,8) ,(2,-4)
The slope is given by
m = (y₂-y₁) /(x₂-x₁)
m = (-4 - 8 )/(2 +1)
m = -12/3
m = -4
Therefore the slope of the given line in the image is -4 , Option A is the answer.
To know more about Straight Line equation
https://brainly.com/question/959487
#SPJ1
hw to solve 6x-12/3+4=18/x
Answers
The two solutions of the equation:
(6x - 12)/3 + 4 = 18/x
Are x = 3 and x = -3
How to solve the equation?Here we have the following equation:
(6x - 12)/3 + 4 = 18/x
Notice that in the right side we have x on a denominator, then x can not be zero, so x ≠ 0.
Now, let's start by simplifying the left side:
(6x - 12)/3+ 4 = 18/x
2x - 4 + 4 = 18/x
2x = 18/x
Now we can multiply both sides by x so we get:
2x^2 = 18
Now divide both sides by 2:
x^2 = 18/2
x^2 = 9
Finally, apply the square root in both sides:
√x^2 = ±√9
x = ±3
The two solutions are x = 3 and x = -3
Learn more about equations:
https://brainly.com/question/22688504
#SPJ1
can someone tell me the error in this problem

Answers
Answer:
You got your negatives messed up. The answer was -5y-4x
Step-by-step explanation:
Expression: -8y + 5x + 3y -9x
Your objective: Simplify the expression
The First step, Combine like terms meaning -8y+3y and -9x+5x
Solve, -8y+3y
That would equal -5y
Next solve -9x + 5x
That would equal -4x
Write your expression in simplest form:
-5y-4x
What you did:
You combined like terms but didn't follow the negative rules
Remember: Positive and Negative = Negative
Negative and Negative = Positive
For example -8y + 3y
You chose to add -8 and 3 which you got -11
What you were supposed to do was to subtract.
A helpful trick: Since they are like terms you could rearrange the questions like this 3y-8y+5x-9x, You can see that you have to do subtraction left to right
3y-8y= -5y
5x-9x= -4x
Solution: -5x-4x
Of(x) = x² - 6x-1-
Mark thic and return
24
-10-8-8-22-
-8
-8
-10
2
B
8 10 x
What is the axis of symmetry
Answers
The axis of symmetry of the function f(x) = x² - 6x-1 is equal to 3.
How to determine the axis of symmetry of a quadratic function?In Mathematics, the axis of symmetry of a quadratic function can be calculated by using this mathematical equation:
Axis of symmetry, Xmin = -b/2a
Where:
a and b represents the coefficients of the first and second term in the quadratic function.
By substituting the parameters, we have the following:
Axis of symmetry, Xmin = -b/2a
Axis of symmetry, Xmin = -(-6)/2(1)
Axis of symmetry, Xmin = 6/2
Axis of symmetry, Xmin = 3.
Read more on quadratic functions here: brainly.com/question/14201243
#SPJ1
A distribution with three or more peaks is said to be
Answers
When a distribution has three or more peaks then it is said to be a multimodal distribution .
What are the types of distributions ?In histograms, there are often three types of distributions which are classified according to the number of peaks that they have . A unimodal distribution would be a histogram that has a single peak in its distribution .
Then there are binomial distributions which boast of having two peaks , Then finally, there is the multimodal distribution which is for all distributions with either three peaks, or more than that .
Find out more on distributions at https://brainly.com/question/13244416
#SPJ1
help please thank you

Answers
Answer:
B
Step-by-step explanation:
If f(x) = 2x +1 and g(x) = -x2,
Answers
The value of (f·g)(x) from the given function is -2x³ - x².
The given functions are f(x) = 2x +1 and g(x) = -x².
What is the function?Functions are the fundamental part of the calculus in mathematics. The functions are the special types of relations. A function in math is visualized as a rule, which gives a unique output for every input x.
Here,
(f·g)(x) = f(x) × g(x)
= (2x +1) × (-x²)
= 2x × (-x²) + 1 × (-x²)
= -2x³ - x²
Therefore, the value of (f·g)(x) from the given function is -2x³ - x².
To learn more about the function visit:
https://brainly.com/question/28303908.
#SPJ1
"Your question is incomplete, probably the complete question/missing part is:"
If f(x) = 2x +1 and g(x) = -x², then find (f·g)(x).
Could someone please help me with this equation, thank you.
-8 + x/5 = 12
Answers
Answer:
x = 100
Step-by-step explanation:
1. To get rid of the denominator of 5, multiply both sides of the equation to get 5
-40 + x = 60
2. Add 40 on both sides to get the variable x by itself
x = 60 + 40
3. Solve
x = 100
Answer:
x=100
Step-by-step explanation:
-8+x/5=12
--8+x/5=12+8
x/5=20
5*20=100
x=100
Leanna has a rectangular piece of fabric. The fabric is 24 inches wide and 40 inches long. Leanna folds the piece of fabric along its diagonal to form a triangular scarf.
What is the area, in square inches, of the triangular scarf?
Answers
Answer:
480 square inches
Step-by-step explanation:
width = base = 24 inches
length = height = 40 inches
area of the triangular scarf = 1/2 * base * height
= 1/2 * 24 * 40
= 480 square inches
State whether or not the given side lengths would form a right triangle: 1, 2, 5
Answers
MARK BRAINLIEST
Answer:
No
Step-by-step explanation:
A triangle is valid if sum of its two sides is greater than the third side. If three sides are a, b and c, then three conditions should be met. 1+2<5
Find the value of x for which I is parallel to m. The diagram is not
to scale.

Answers
Answer:
b 56
Step-by-step explanation: