a die is rolled until the first time t that a six turns up, what is the probability distribution for t
Answers
The probability of rolling a six on any given roll is constant, so the probability distribution is a geometric distribution.
What is a probability distribution?
A probability distribution is a function that describes the probabilities of different outcomes in a random event or experiment. It is used to represent the likelihood of different outcomes occurring in a given situation.
In the case of rolling a die until the first time that a six turns up, the probability distribution for t (the number of rolls it takes to get a six) would describe the probability of getting a six on each roll.
The probability of getting a six on the first roll is 1/6, since there is a 1 in 6 chance of rolling a six on any given roll. The probability of getting a six on the second roll is 1/6, since there is still a 1 in 6 chance of rolling a six on any given roll. The probability of getting a six on the third roll is also 1/6, and so on.
The probability distribution for t in this case can be represented by the following table:
t Probability
1 1/6
2 1/6
3 1/6
4 1/6
5 1/6
... ...
This probability distribution indicates that the probability of getting a six on the first roll is 1/6, the probability of getting a six on the second roll is 1/6, and so on.
Hence, the probability of rolling a six on any given roll is constant, so the probability distribution is a geometric distribution.
To learn more about the probability distribution, visit:
https://brainly.com/question/24756209
#SPJ4
Related Questions
PRE CALC HELP NEEDED

Answers
Answer:
\(\dfrac{5e^2}{2}\)
Step-by-step explanation:
Differentiation is an algebraic process that finds the slope of a curve. At a point, the slope of a curve is the same as the slope of the tangent line to the curve at that point. Therefore, to find the slope of the line tangent to the given function, differentiate the given function.
Given function:
\(y=x^2\ln(2x)\)
Differentiate the given function using the product rule.
\(\boxed{\begin{minipage}{5.5 cm}\underline{Product Rule for Differentiation}\\\\If $y=uv$ then:\\\\$\dfrac{\text{d}y}{\text{d}x}=u\dfrac{\text{d}v}{\text{d}x}+v\dfrac{\text{d}u}{\text{d}x}$\\\end{minipage}}\)
\(\textsf{Let\;$u=x^2}\)\(\textsf{Let\;$u=x^2$}\implies \dfrac{\text{d}u}{\text{d}x}=2x\)
\(\textsf{Let\;$v=\ln(2x)$}\implies \dfrac{\text{d}v}{\text{d}x}=\dfrac{2}{2x}=\dfrac{1}{x}\)
Input the values into the product rule to differentiate the function:
\(\begin{aligned}\dfrac{\text{d}y}{\text{d}x}&=u\dfrac{\text{d}v}{\text{d}x}+v\dfrac{\text{d}u}{\text{d}x}\\\\&=x^2 \cdot \dfrac{1}{x}+\ln(2x) \cdot 2x\\\\&=x+2x\ln(2x)\end{aligned}\)
To find the slope of the tangent line at x = e²/2, substitute x = e²/2 into the differentiated function:
\(\begin{aligned}x=\dfrac{e^2}{2}\implies \dfrac{\text{d}y}{\text{d}x}&=\dfrac{e^2}{2}+2\left(\dfrac{e^2}{2}\right)\ln\left(2 \cdot \dfrac{e^2}{2}\right)\\\\&=\dfrac{e^2}{2}+e^2\ln\left(e^2\right)\\\\&=\dfrac{e^2}{2}+2e^2\\\\&=\dfrac{5e^2}{2}\end{aligned}\)
Therefore, the slope of the line tangent to the graph of y = x²ln(2x) at the point where x = e²/2 is:
\(\boxed{\dfrac{5e^2}{2}}\)
what is relative intrest
Answers
Relative interest refers to the comparison of interest rates between different financial instruments or investment opportunities. It allows individuals or investors to assess and evaluate the attractiveness of various options based on their potential returns.
1. Understand the basic concept: Interest is the cost of borrowing money or the return earned on invested funds. Relative interest involves comparing the interest rates of different financial instruments or investments to determine which one offers a more favorable return.
2. Identify the investment options: Start by identifying the different investment opportunities or financial instruments available. These can include savings accounts, certificates of deposit (CDs), bonds, stocks, or other investment vehicles.
3. Research interest rates: Research and gather information about the current interest rates offered by each investment option. This information can usually be found on financial websites, through financial institutions, or by consulting with a financial advisor.
4. Compare interest rates: Once you have the interest rates for each investment option, compare them side by side. Look for the differences in rates and identify which options offer higher or lower returns.
5. Assess risk and return: Consider the level of risk associated with each investment option. Higher returns often come with higher risk, so it's essential to evaluate the risk-reward tradeoff.
6. Make an informed decision: Based on the comparison of interest rates and the risk-reward assessment, make an informed decision on which investment option aligns with your financial goals and risk tolerance.
Always remember to consider your financial goals, risk tolerance, and consult with a financial advisor if needed.
For more such questions on interest rates, click on:
https://brainly.com/question/25720319
#SPJ8
The graph of y=x is shifted 4 units up and 3 units right. Which equation represents the new graph?
O
y = -√-3+4
O
y=-√x+3+4
O
y=-x-4 + 3
y = -x + 4 + 3
Answers
Answer:
y = -√(x - 3) + 4
Step-by-step explanation:
On shifting 4 units up
y = -√x + (4)y = -√x + 4On shifting 3 units right
y = -√(x - 3) + 4y = -√(x - 3) + 4Option 1Answer:
\(\textsf{A)} \quad y=-\sqrt{x-3}+4\)
Step-by-step explanation:
Translations
For \(a > 0\)
\(f(x+a) \implies f(x) \: \textsf{translated}\:a\:\textsf{units left}\)
\(f(x-a) \implies f(x) \: \textsf{translated}\:a\:\textsf{units right}\)
\(f(x)+a \implies f(x) \: \textsf{translated}\:a\:\textsf{units up}\)
\(f(x)-a \implies f(x) \: \textsf{translated}\:a\:\textsf{units down}\)
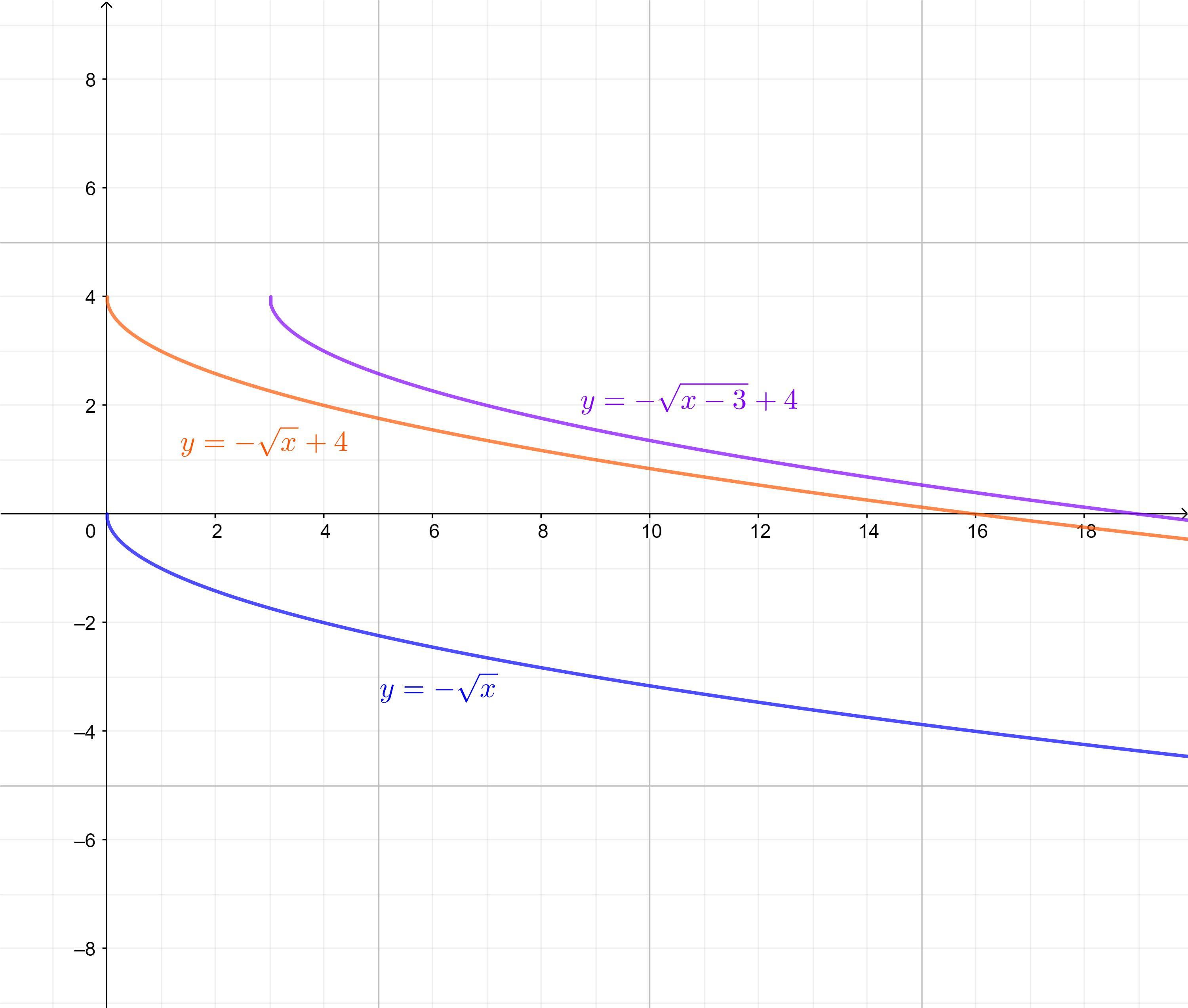
Parent function (shown in blue on attached diagram):
\(y=-\sqrt{x}\)
Shifted 4 units up (shown in orange on attached diagram):
\(\implies y=-\sqrt{x}+4\)
Shifted 3 units right (shown in purple on attached diagram):
\(\implies y=-\sqrt{x-3}+4\)
In a study, 8 people ate a total of 1,376 pounds of potatoes in 2 years.
If each person ate the same amount each year, how many pounds of potatoes did each person eat in 1 year?
Answers
Answer:
86 pounds of potatoes per 1 person
Step-by-step explanation:
Divide 1,376 by 2 to get how many potatoes were eaten in 1 year, answer is 688. Then divided 688 by 8 to find how many pounds of potatoes where eaten by 1 person in 1 year, answer is 86.
86 pounds of potatoes is how much 1 person ate in 1 year.
Plz help i need helpful plz

Answers
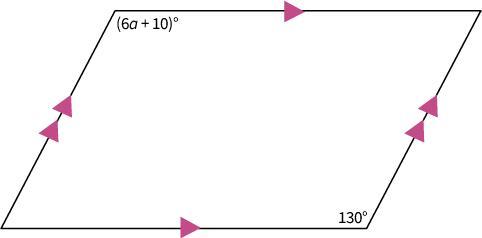
Find the value of a. a) 15 b) 10 c) 25 d) 20
Answers
Answer:
answer d) 20
Step-by-step explanation:
Because the two lines are parallel two by two, the figure is a parallelogram.
In a parallelogram the opposite corners are identical.
Given:
opposite corner1 = 130°
opposite corner2= (6a + 10)°
Because corner1 = corner2 we now have:
(6a + 10) = 130
6a + 0 = 130 -10
6a = 120
a = 20
Which is answer d).
One ratio you could use for converting units is 1.000 kilograms 1 gram O A. True O B. False SUB
Answers
The statement that the ratio 1.000 kilograms to 1 gram can be used for converting units is false. The correct Ratio is 1 kilogram to 1000 grams.
The statement "One ratio you could use for converting units is 1.000 kilograms to 1 gram" is false.
When converting units, it is important to use the correct conversion factors that relate the two units being converted. In this case, the ratio given is 1.000 kilograms to 1 gram, which implies that 1 kilogram is equal to 1 gram. However, this is incorrect.
The correct conversion factor between kilograms and grams is that 1 kilogram is equal to 1000 grams. This means that to convert kilograms to grams, you multiply the value in kilograms by 1000. Conversely, to convert grams to kilograms, you divide the value in grams by 1000.
So, the correct ratio for converting kilograms to grams is 1 kilogram to 1000 grams, or 1:1000. Therefore, the statement that the ratio 1.000 kilograms to 1 gram can be used for converting units is false. The correct ratio is 1 kilogram to 1000 grams.
For more questions on Ratio .
https://brainly.com/question/12024093
#SPJ8
Suppose the probability that a US resident has traveled to Canada is 0.12, to Mexico is 0.20, and to both
countries is 0.04. Round your answers to two decimal places. (11 pts)
a) Create a Venn diagram for the scenario above.
What is the probability that a US resident chosen at random has traveled to Canada but not Mexico?
c) What is the probability that a US resident chosen at random has traveled to Canada or Mexico?
d) What is the probability that a US resident chosen at random has not traveled to either Canada or
Mexico?
e) What is the probability that a US resident chosen at random has traveled to Mexico given they have
traveled to Canada?
Answers
Answer:
a is what I have for your answer
ALGEBRA please put a very small explanation to the awnser


Answers
Certainly! The problem can be solved using the Pythagorean theorem,
which states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
In this case, the ladder acts as the hypotenuse, and we need to find the length of the vertical side (height) it reaches up the wall.
The ladder forms the hypotenuse, and its length is given as 12 meters. The distance from the foot of the ladder to the base of the wall represents one side of the triangle, which is 4.5 meters.
By substituting the given values into the Pythagorean theorem equation: (12m)^2 = h^2 + (4.5m)^2, we can solve for the unknown height 'h'.
Squaring 12m gives us 144m^2, and squaring 4.5m yields 20.25m^2. By subtracting 20.25m^2 from both sides of the equation, we isolate 'h^2'.
We then take the square root of both sides to find 'h'. The square root of 123.75m^2 is approximately 11.12m.
Therefore, the ladder reaches a height of approximately 11.12 meters up the wall.
For more questions Pythagorean theorem:
https://brainly.com/question/343682
#SPJ8
what value of X makes the model true?

Answers
The value of x is -1 which makes the model true
The equation from the given model will be 5x+6=1
We have to find the value of x
5x+6=1
Subtract 6 from both sides
5x=-5
Divide both sides by 5
x=-1
Hence, the value of x is -1 which makes the model true
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ1
LESSON 17 SESSION 3
4 Ms. Duda's class is hanging 500 red lanterns around the
school for Lunar New Year. Before lunch, the class hangs
100 of the lanterns.
PART A Draw a model to show what percent of 500 lanterns
the class hangs before lunch.
Answers
The model should visually represent that Ms. Duda's class hung 100 lanterns before lunch, which is 20% of the total 500 lanterns.
To draw a model showing what percent of 500 lanterns Ms. Duda's class hangs before lunch, we can use a rectangular bar model.
Draw a rectangular bar to represent the total number of lanterns, which is 500. Label it as "Total Lanterns."
Divide the rectangular bar into two parts. One part should represent the number of lanterns hung before lunch, which is 100. Label this section as "Lanterns Before Lunch."
Calculate the percentage of lanterns hung before lunch by dividing the number of lanterns hung before lunch by the total number of lanterns and multiplying by 100. In this case, (100/500) * 100 = 20%.
Draw an arrow pointing to the "Lanterns Before Lunch" section, and write "20%" next to it to represent the percentage.
The model should visually represent that Ms. Duda's class hung 100 lanterns before lunch, which is 20% of the total 500 lanterns.
To learn more about the percentage;
https://brainly.com/question/24159063
#SPJ1
{Edmentum}Which operation should you perform last in the expression 12 × 4^2?
No sample answer, please?
Have good defined answer! :D
Also, If you put a sample answer put a warning and I'll mix it into my own words! :D
That's all, Open to suggestion work and support work!
Have a amazing Day!
__________________¶¶¶¶¶
_______________¶¶¶¶¶__¶¶________¶¶¶¶¶¶¶¶
__________¶¶¶¶__¶¶¶¶___¶¶_____¶¶¶¶¶____¶¶
______¶¶¶___¶¶¶¶________¶¶_¶¶¶______¶¶¶
___¶¶¶_¶¶¶¶______________¶¶_______¶¶¶
¶¶¶_¶¶¶¶________________¶¶______¶¶¶
¶¶¶¶_________________¶¶¶_____¶¶¶
¶¶________________¶¶¶_____¶¶¶
¶¶_____________¶¶¶_____¶¶¶
_¶¶________¶¶¶¶____¶¶¶¶
__¶¶____¶¶¶_____¶¶¶¶
___¶¶_¶¶¶¶___¶¶¶¶
____¶¶_____¶¶¶¶
__¶¶_____¶¶¶¶
¶¶____¶¶¶¶
¶¶_¶¶¶¶
¶¶¶¶¶_____¶¶¶¶¶___________¶¶¶¶¶
_________¶¶¶¶¶¶¶_________¶¶¶¶¶¶¶
_________¶¶¶¶¶¶¶_________¶¶¶¶¶¶¶
__________¶¶¶¶¶___________¶¶¶¶¶
__¶¶¶¶_____________________________¶¶¶¶
_¶¶¶¶¶¶___________________________¶¶¶¶¶
__¶¶¶¶¶¶_________________________¶¶¶¶¶¶
___¶¶¶¶¶¶_______________________¶¶¶¶¶¶
____¶¶¶¶¶¶¶___________________¶¶¶¶¶¶¶
______¶¶¶¶¶¶¶_______________¶¶¶¶¶¶¶
_________¶¶¶¶¶¶___________¶¶¶¶¶¶
____________¶¶¶¶¶¶¶¶¶¶¶¶¶¶¶¶¶
______________¶¶¶¶¶¶¶¶¶¶¶¶
Answers
Let f ( x ) = a x n − b x 2 + 14 c x m + d x 3 − 7 f(x)= cx m +dx 3 −7 ax n −bx 2 +14 f, left parenthesis, x, right parenthesis, equals, start fraction, a, x, start superscript, n, end superscript, minus, b, x, squared, plus, 14, divided by, c, x, start superscript, m, end superscript, plus, d, x, cubed, minus, 7, end fraction, where m mm and n nn are integers and a aa, b bb, c cc and d dd are unknown constants. Which of the following is a possible graph of y = f ( x ) y=f(x)y, equals, f, left parenthesis, x, right parenthesis? Choose 1 answer:
Answers
The graph in option C is the one that best satisfies the function y = f ( x ) y=f(x)y, equals, f, left parenthesis, x, right parenthesis
How to solveThe ultimate exponent of the equation, \(x^n or x^m\), is the key factor that determines the end behavior amid a graph.
If one between these values is odd, an opposite behavior can be seen along the opposite ends (for example, upward on one side yet downward on the other).
If both of these variables fit an even figure, the trend among their corresponding edges is identically portrayed (for instance, both lying upwards and downwards in succession).
The \(x^3\) term, however, will sway the overall form between such high-powered terms.
Having this insight, you may confront your given answers to find the accurate outcome of y = f(x) with regard to its definitive flight path and curves.
Solving the given problem:
f ( x ) = \(\frac{ax^2 - bx^2 + 14}{cx^2 + dx^2 -7}\)
At x= 0 on the y- axis
f(0) = \(\frac{0-0 + 14}{0 +0 - 7}\)
Thus, only option C satisfies this condition.
Read more about graphs here:
https://brainly.com/question/26233943
#SPJ1

What is the length segment of BC

Answers
A fish bowl contains blue, green and red plastic fish. When a fish is picked out at random, the probability of it being blue is 0.7 and the probability of it being green is 0.2. A prize is given if a red fish is picked out. What is the probability of Matt picking a red fish? (Give your answer as a decimal.) There are 60 fish in the fish bowl. How many of the fish are red?
Answers
Answer:
0.1 probability of Matt picking a red fish
6 of the fish are red.
Step-by-step explanation:
We have these following probabilities:
70% = 0.7 probability that the fish is blue.
20% = 0.2 probability that the fish is green.
p probability that the fish is red.
The sum of all these probabilities is 100% = 1. So
0.7 + 0.2 + p = 1.
p = 0.1
0.1 probability of Matt picking a red fish
There are 60 fish in the fish bowl. How many of the fish are red?
n trials with p probability of sucess. The expected value is
\(E(X) = np\)
Here we have \(n = 60, p = 0.1\). So
\(E(X) = np = 60*0.1 = 6\)
6 of the fish are red.
The probability of Matt at the time of picking a red fish is 0.1.
And, The number of fish that should be red is 6.
Calculation of the probability:Since
There is a 70% probability when the fish is blue
And, 20% probability when the fish is green.
Now
Here we assume p be the probability in the case when the fish is red.
So,
Here the sum of probabilities should be 100% i.e. equal to 1.
Now
The following calculation is to be done
0.7 + 0.2 + p = 1
0.9 + p = 1
So,
p = 0.1
Now for the red one it should be
= 60 (0.1)
= 6
Hence, The probability of Matt at the time of picking a red fish is 0.1.
And, The number of fish that should be red is 6.
Learn more about probability here: https://brainly.com/question/10695144
An 8-sided number cube is rolled 4000 times. The number 2 appeared 200 times. Determine the theoretical and experimental probability of rolling a 2 in order to determine the fairness of the number cube. Drag values or words to the boxes to correctly complete the statements.
Answers
Theoretical Probability of rolling a 2= 1/20
Experimental Probability of rolling a 2 = 1/20
Theoretical probability of rolling a 2:
The theoretical probability of an event is the ratio of the number of favourable outcomes to the total number of possible outcomes. Since there are 8 sides to the cube, the total number of possible outcomes is 8. Since the number 2 appeared 200 times out of 4000 rolls, the number of favorable outcomes is 200. Therefore, the theoretical probability of rolling a 2 is:
Theoretical Probability of rolling a 2 = Number of favourable outcomes / Total number of possible outcomes = 200/4000 = 1/20
Experimental probability of rolling a 2:
The experimental probability of an event is the ratio of the number of times the event occurred to the total number of trials. In this case, the event is rolling a 2, which occurred 200 times out of 4000 rolls.
Therefore, the experimental probability of rolling a 2 is:
Experimental Probability of rolling a 2 = Number of times the event occurred / Total number of trials = 200/4000 = 1/20
Comparing theoretical and experimental probability:
If the cube is fair, we would expect the theoretical probability and the experimental probability to be similar. In this case, both probabilities are 1/20, which means that the cube appears to be fair. However, we would need to conduct more trials to be more confident in our conclusion.
For such more questions on Probability
https://brainly.com/question/251701
#SPJ8
Can anyone help me in less than 5 minutes cuz I’m in school at the moment and still on unit 1 and supposed to be on unit 7 today
If ur available at anytime my number is

Answers
Answer:
I think C
Step-by-step explanation:
It has a whole number as numerator and denominator so it is rational and it is a real number, but it is not an integer because it is a fraction.
Answer:
Rational, and Real numbers.
Step-by-step explanation:
There's a certain overlapping sequence of categorizing:
Whole #, Integers, Rational, Real.
Fractions and decimals belong in Rational, so you could say they are real as well.
Hope this helps! (sorry about it being brief)
i need help really fast

Answers
John's monthly salary is $810. He spends 5/9 of it on rent, 1/3 of it on
food and saves the rest. How much money does he save in a year?
Answers
Answer:
$1080
Step-by-step explanation:
monthly salary = $810
money spent on rent = 810 × 5/9 = $450
money spent on food = 810 × 1/3 = $270
money saved in a month = monthly salary - (money spent on [rent + food])
= 810 - (450 + 270)
= 810 - 720 = $90
money saved in a year = money saved in a year × 12
90 × 12 = $1080
OR
monthly salary = $810
yearly salary = 810 × 12 = $9720
money spent on rent = 9720 × 5/9 = $5400
money spent on food = 9720 × 1/3 = $3240
money saved in one year =
yearly salary - (money spent on [rent + food] in an year )
= 9720 - (5400 + 3240)
= 9720 - 8640 = $1080
What’s the answer to If =3+23
, what is
when =1
and =2
?

Answers
The value of y when a = 1 and b = 2 is 22.
How to solve an equation?The equation of can be solved as follows: We will substitute the value of a and b in the equation to find the value of y.
Therefore,
y = 3ab + 2b³
Let's find y when a = 1 and b = 2
Hence,
y = 3(1)(2) + 2(2)³
y = 6 + 2(8)
y = 22
Therefore,
y = 22
learn more on equation here: https://brainly.com/question/29663159
#SPJ1
Bert's birthday party will cost $246 if he invites 41 guests. How many guests can there be, at most, if Bert can afford to spend a total of $534 on his birthday party? Solve using unit rates. guests
Answers
If Thiyo maintained a steady speed, how far did he drive after 3 h? Enter your answer into the box.


Answers
168 miles
Explanations:According to the given question, we have the following parameters:
Speed of Thiyo = 56mi/hr
If Thiyo drives for 3 hours, the distance covered is given as:
\(\begin{gathered} \text{Distance}=\text{Speed}\times\text{time} \\ \text{Distance}=\frac{56mi}{\cancel{hr}}\times3\cancel{\text{hrs}} \\ Distance=56mi\times3 \\ \text{Distance}=168\text{miles} \end{gathered}\)Therefore Thiyo covered a distance of 168 miles in 3hrs
Find the interest for one interest period. The account balance is $685, the APR is
5.1% and interest is quarterly. What is the amount of interest rounded to the
nearest cent?
Answers
Step-by-step explanation:
step 1. A = P(1 + r/n)^nt. this is the compounding equation where n is the number of compounds, t is the time in years, and r is the rate.
step 2. A = 685(1 + .051/1)^(1(1/4))
step 3. A = 693.57.
can you do 1 2 and 3

Answers
Answer: can you do 1 2 and 3
Step-by-step explanation:
Who knows these? Need them asap please

Answers
Answer:
7)55.6
9) 11.25
11)238.18
Step-by-step explanation:
7) ;et x be the number
so the price is $139 but there is a discount of 40%. how much does she save?
so, $139=100%
x=100%-40%( why we said like this? coz am trying to show how much she will pay, if there was 40% off then she will pay the 60% only of the price)
$139=100%
x=60%, criss cross
x=$139*60%/100%
x=83.4
then to find how much she saves, the original price - x
$139-83.4
=$55.6
9) let x be the number
the original price was $75 and there were a discount for the table for 15% off.
so,
$75=100% (why we make 100%?, coz it says the original price is 75, got it?)
x=100%-15%
x=85%
so , $75=100%
$x=85%, criss cross
100%x=85*75
x=63.75, but the question says how much does she save?|
so the original price minus x
75-63.75 = 11.25
11) let x be the number
she got a rise of 32% per hour. so 100%+32 is 132%
$314.40 for a 40-hour week
$314.4=132%
x=100%, criss cross
$314.4*100=132x
x=31440/132
x=238.18
and the 238.18 is what she used to earn for a 40-hour week before her rise.
Hope it helped:)
MATH 144 : College Math

Answers
Miguel will need to deposit approximately $3,261.25 into the annuity each year for 8 years in order for the annuity to have a total value of $24,000.
What is the annuity?
An annuity is a contract between you and an insurance company that requires the insurer to make payments to you, either immediately or in the future. You buy an annuity by making either a single payment or a series of payments.
We can use the formula for the future value of an annuity:
FV = PMT * \(((1 + r)^n - 1) / r\)
where FV is the future value, PMT is the regular payment, r is the interest rate per compounding period, and n is the number of compounding periods.
In this problem, we want to solve for PMT, given that FV = $24,000, r = 6.6%, n = 8, and payments are made at the end of each year.
First, we need to calculate the interest rate per year, since the annuity is compounded annually:
i = r / 100 = 6.6% / 100 = 0.066
Next, we can plug in the values and solve for PMT:
24000 = PMT *\(((1 + 0.066)^8 - 1) / 0.066\)
24000 = PMT * 7.3605
PMT = 24000 / 7.3605
PMT ≈ $3,261.25
Hence, Miguel will need to deposit approximately $3,261.25 into the annuity each year for 8 years in order for the annuity to have a total value of $24,000.
To learn more about annuity, Visit
https://brainly.com/question/25792915
#SPJ1
The output from a statistical software package indicates that the mean and standard deviation of a data set consisting of measurements are $ and $, respectively. a. What are the units of measurement of the variable of interest? A. Units B. Dollars Your answer is correct.C. Single measurements
Answers
Answer: dollars
Step-by-step explanation:
Mean means average and it's calculated by adding the numbers given and then dividing the sum by the amount of numbers that were given.
The standard deviation shows the amount of dispersion or amount of variation of a given set of values. From the question, the only unit of measurement we can see is the dollar sign($).
In response to the increasing weight of airline passengers, the Federal Aviation Administration in 2003 told airlines to assume that passengers average 190 pounds in the summer, including clothing and carry‑on baggage. But passengers vary, and the FAA did not specify a standard deviation. A reasonable standard deviation is 35 pounds. Weights are not normally distributed, especially when the population includes both men and women, but they are not very non‑Normal. A commuter plane carries 22 passengers. What is the approximate probability P that the total weight of the passengers exceeds 4500 pounds? Use the four‑step process to guide your work. Give your answer as a percentage precise to two decimal places. P=___?
Answers
The approximate probability P that the total weight of the passengers exceeds 4500 pounds is 10.03%.
Probability is a measure of the likelihood of an event to occur. Many events cannot be predicted with total certainty. We can predict only the chance of an event to occur i.e., how likely they are going to happen, using it. Probability can range from 0 to 1, where 0 means the event to be an impossible one and 1 indicates a certain event.
The probability formula is defined as the possibility of an event to happen is equal to the ratio of the number of favorable outcomes and the total number of outcomes.
Probability of event to happen P(E) = Number of favorable outcomes/Total Number of outcomes
Total of 22 is more than 4500 is equivalent to average of 22 is more than \($\frac{4500}{22}\)=204.545
\($$\begin{aligned}P(\bar{x} > 204.545) & =1-P(\bar{x} < 204.545) \\& =1-P\left(\frac{\bar{x}-\mu}{\sigma / \sqrt{u}} < \frac{204.545-195}{35 / \sqrt{22}}\right) \\& =1-P(z < 1.2792) \\\end{aligned}$$\)
= 1 - 0.8997
= 0.1003
= 10.03%
Therefore, the approximate probability P that the total weight of the passengers exceeds 4500 pounds is 10.03%.
For more such questions on Probability
https://brainly.com/question/12905909
#SPJ4
Find a and b using the factor theorem.
\(f(x)=x^3+ax^2+bx-12\) has factor \((x-1), (x+1)\)
Answers
The values of a and b using the factor theorem for the polynomial f(x), we set f(1) and f(-1) equal to zero. Solving the resulting system of equations, we find that a = 12 and b = -1.
To find the values of a and b using the factor theorem, we need to use the given factors (x - 1) and (x + 1) and the fact that they are roots of the polynomial f(x).
The factor theorem states that if (x - c) is a factor of a polynomial, then f(c) = 0. Therefore, we can set x = 1 and x = -1 in the polynomial f(x) to get two equations.
First, let's substitute x = 1 into f(x):
f(1) = (1)^3 + a(1)^2 + b(1) - 12
f(1) = 1 + a + b - 12
Next, let's substitute x = -1 into f(x):
f(-1) = (-1)^3 + a(-1)^2 + b(-1) - 12
f(-1) = -1 + a - b - 12
Since (x - 1) and (x + 1) are factors, f(1) and f(-1) must equal zero. Therefore, we can set the two equations equal to zero and solve for a and b:
1 + a + b - 12 = 0
-1 + a - b - 12 = 0
Rearraning the equations, we have:
a + b = 11
a - b = 13
Now, we can solve this system of equations. Adding the two equations, we get:
2a = 24
a = 12
Substituting the value of a into one of the equations, we find:
12 - b = 13
b = -1
Therefore, the values of a and b are 12 and -1 respectively.
For more such questions on polynomial
https://brainly.com/question/1496352
#SPJ8
Review the graph.
On a coordinate plane, a circle has center (4, 0) and radius 4. Another circle has center (2, negative 3) and radius 6. The area inside of the first circle and outside of the second circle between the 2 circles is shaded.
Which system of inequalities is shown in the graph?
36 > (x + 3)2 + (y – 2)2 and 16 > (x – 4)2 + y2
36 > (x – 2)2 + (y + 3)2 and 16 > (x – 4)2 + y2
36 < (x + 3)2 + (y – 2)2 and 16 > (x – 4)2 + y2
36 < (x – 2)2 + (y + 3)2 and 16 > (x – 4)2 + y2

Answers
Answer:
36 < (x - 2)² + (y + 3)² and 16 > (x - 4)² + y²
Step-by-step explanation:
This is because the shaded area is inside the first circle (centered at (4, 0) with a radius of 4) but outside the second circle (centered at (2, -3) with a radius of 6). The inequalities reflect these conditions by setting the inequality signs accordingly. The inequality with "<" for the first circle ensures that the shaded area is within the circle, and the inequality with ">" for the second circle ensures that the shaded area is outside the circle.