A linear function has a rate of change of 5 and initial value of 13. What is y when x=11?
Answers
Answer:
y=68
Step-by-step explanation:
y=5x+13
y=5(11)+13
y=55+13
y=68
Related Questions
write the equation of the line in slope-intercept form. It has a coefficient of m=-1 and pass through the point (9,4)
Answers
Answer:
y=-1x+13
Step-by-step explanation:
There is a negative slope we start at (9,4) and go up one and to the left one. Eventually we well pass the y-axis at 13.
1) A survey asked 200 Grade 4 students about their reading preferences. Based on Graph #1, about how many of them would you expect prefer comic books?
about how many students prefer literature (poems, plays, or novels)?
A. 45
B. 90
C. 100
D. 130
E. 180

Answers
answer:B. 90 good luck I hope you pass
The answer is B which is 90
What is the area of this parallelogram? A = 20 ft² A=2123 ft² A=3313 ft² A=4123 ft².
Answers
Answer:
Step-by-step explanation:
where's the parallelogram?
The figure below was made with a scale of 1 unit =9 m. You can place your figure anywhere on the grid on the right.

Answers
Answer & Step-by-step explanation:
I can't draw the image, but I can explain it to you.
Since 1 unit was 3 units and now it's 9, you would have to divide each side by 3. So, the width would be 1 unit and the length would be 2 units.
I hope this helped!!!
The scale of 1 unit = 9 m
The rectangle 1 unit = 3 m is similar to 1 unit = 9 m
Since the unit of the scale is reduced the image size will be smaller than the given diagram.
What is supposed by similarity in math?In Euclidean geometry, objects are comparable if they have an identical shape, or if one has the same form because they reflect a photograph of the other. more precisely, one can be obtained from the opposite by using uniformly scaling (enlarging or lowering), probably with extra translation, rotation and reflection.
Learn more about the unit here: https://brainly.com/question/25862883
#SPJ2

what is the product of 8.2 Ãâ€"" 109 and 4.5 Ãâ€"" 10-5 in scientific notation? 36.9 Ãâ€"" 10-45 12.7 Ãâ€"" 104 3.69 Ãâ€"" 105 3.69 Ãâ€"" 1014
Answers
The product of 8.2 × 10^9 and 4.5 × 10^-5 in scientific notation can be found by multiplying the coefficients and adding the exponents.
Step 1: Multiply the coefficients: 8.2 × 4.5 = 36.9.
Step 2: Add the exponents: 10^9 × 10^-5 = 10^(9-5) = 10^4.
So, the product is 36.9 × 10^4.
To express this in scientific notation, we need to move the decimal point to the right until there is only one non-zero digit to the left of the decimal point.
Step 3: Move the decimal point 4 places to the right: 36.9 × 10^4 = 3.69 × 10^5.
We can find the product of two numbers in scientific notation by multiplying the coefficients and adding the exponents. In this case, we multiplied 8.2 by 4.5 to get 36.9 and added 9 and -5 to get 4. The final answer is 3.69 × 10^5.
The product of 8.2 × 10^9 and 4.5 × 10^-5 in scientific notation is 3.69 × 10^5.
To know more about product visit
https://brainly.com/question/33332462
#SPJ11
Please answer question 14. A and B.

Answers
Answer:
A. ≈31.1
B. ≈19.7
Step-by-step explanation:
A. 245/798
B. 157/798
Answer:
Look at step-by-step explanation
Step-by-step explanation:
14a.
There are 798 students total and 245 freshman. To find the percent of freshman, divide 245 by 798:
245/789= 31.1%
Same process for part b. There are 798 students and 157 seniors:
157/789= 20.0%
students who score within 22 points of the number 78 will pass a particular test. write this statement using absolute value notation and use the variable x for the score.
Answers
The statement using absolute value notation will be x - 78 ≤ 22.
The student will pass the test which scores 22 points for the number 78
Absolute values are any digit's value without taking the sign into an account. Therefore, all negative numbers will be regarded as positive for absolute value. The absolute value of -5, for instance, will be 5, whereas that of -7, will be 7.
In essence, the absolute value calculates the distance from zero. Putting an absolute value on something does not imply that they are the same number but that they are the same distance from 0.
Le the score of student be = x
Forming the absolute value notation -
This can be expressed as,
x - 78 ≤ 22.
Read more about absolute value notation on:
https://brainly.com/question/24504417
#SPJ4
You can work no more than 20 hours next week. You need to earn at least $84 to cover your weekly expenses. Your tutoring job pays $6.50 per hour, and your job as a coffee shop barista pays $8 per hour. Set up a system of inequalities, and determine if doing 5 hours of tutoring and 8 hours of working as a barista is a viable combination.
A. x+y≤20 and 6.5x+8y≥84
Doing 5 hours of tutoring and 8 hours of working as a coffee shop barista is not a viable combination.
B.x+y≤20 and 6.5x+8y≤84
Doing 5 hours of tutoring and 8 hours of working as a coffee shop barista is not a viable combination.
C.x+y≤20 and 6.5x+8y≥84
Doing 5 hours of tutoring and 8 hours of working as a coffee shop barista is a viable combination.
D. x+y≤20 and 6.5x+8y≤84
Doing 5 hours of tutoring and 8 hours of working as a coffee shop barista is a viable combination
help please I have a F and I need it up
Answers
Answer:
x + y ≤20
6.5x + 8y ≥84
Step-by-step explanation:
Doing 5 hours of tutoring and 8 hours of working as a coffee shop barista is not a viable combination..
plz help will give brainliest
CDE is reflected over the Y- Axis

Answers
Answer:
The answer to this question is A
The new coordinates will be C( 3 ,0), D( 7,1) , E(2,4) , Option A is the correct answer.
What is the meaning of Reflection ?When a object or a figure is reflected , it means an mirror image if the object is being created , the shape and size of the object remains same , Only the coordinates change on the basis of the axis used for Reflection.
The figure is given in the question.
The coordinates of the figure is
C( -3 ,0)
D( -7,1)
E(-2,4)
When reflection is done along any axis , the coordinates of the other axis change sign.
so in this case ( x,y ) -----> ( -x,y)
The new coordinates will be
C( 3 ,0)
D( 7,1)
E(2,4)
Therefore Option A is the correct answer.
To know more about Reflection
https://brainly.com/question/15487308
#SPJ2
O
Given the following exponential function, identify whether the change represents
growth or decay, and determine the percentage rate of increase or decrease.
y = 40(0.97)
Growth
% increase Submit Answer
attempt 1 out of 2
Privacy Policy Terms of Service
Copyright © 2022 DeltaMath.com. All Rights Reserved.
NG
Answers
Therefore, the given function represents exponential decay with a percentage rate of decrease of approximately 3%.
What is percent?Percent is a way of expressing a number as a fraction of 100. The word "percent" means "per hundred" or "out of a hundred". It is denoted by the symbol "%". For example, if there are 100 apples and 25 of them are green, we can say that 25% of the apples are green. This means that out of 100 apples, 25 are green. Another example is if the price of a shirt increased from $20 to $25, we can say that the price increased by 25%. This means that the price increased by 25 out of 100 dollars, or 0.25 times the original price. Percentages are commonly used in everyday life, such as in calculating taxes, discounts, interest rates, and other financial calculations.
Here,
The given exponential function is:
y = 40(0.97)ⁿ
where n represents the time variable.
To determine whether the function represents growth or decay, we need to examine the base of the exponent, which is 0.97 in this case. Since the base is less than 1, the function represents exponential decay.
To determine the percentage rate of decrease, we can find the difference between the initial value of y (which is 40) and the value of y after one unit of time has passed (i.e., when n = 1):
y(1) = 40(0.97)¹ ≈ 38.8
The percentage rate of decrease can then be calculated as:
% decrease = [(initial value - final value) / initial value] x 100%
= [(40 - 38.8) / 40] x 100%
≈ 3%
To know more about percent,
https://brainly.com/question/29172752
#SPJ1
Express the answers to the following operations with the proper number of significant figures. (a) 8.370×1.3 ×10 (b) 4.265/2.0 (c) (1.2588×10 ^3)×(1.06×10 ^−2) (d) (1.11) ^1/2
Answers
The answers, rounded to the appropriate number of significant figures, are as follows:
(a) 1.088 ×\(10^2\)
(b) 2.132
(c) 1.3331 ×\(10^1\) and
(d) 1.05.
Let's calculate the answers to the given operations using the appropriate number of significant figures.
(a) 8.370×1.3×10
To perform this multiplication, we multiply the decimal numbers and add the exponents of 10:
8.370 × 1.3 × 10 = 10.881 × 10 = 1.0881 × \(10^2\)
Since the original numbers have four significant figures, we round the final answer to four significant figures:
1.088 × \(10^2\)
(b) 4.265/2.0
For division, we divide the decimal numbers:
4.265 ÷ 2.0 = 2.1325
Since both numbers have four significant figures, the answer should be rounded to four significant figures:
2.132
(c) (1.2588×\(10^3\))×(1.06×\(10^-^2\))
To multiply these numbers, we multiply the decimal numbers and add the exponents:
(1.2588 × \(10^3\)) × (1.06 × \(10^-^2\)) = 1.333128 × \(10^1\)
Since the original numbers have five significant figures, we round the final answer to five significant figures:
1.3331 × \(10^1\)
(d) \((1.11)^(^1^/^2^)\)
To calculate the square root, we raise the number to the power of 1/2:
\((1.11)^(^1^/^2^)\)= 1.0524
Since the original number has three significant figures, the answer should be rounded to three significant figures:
1.05
It's important to note that the significant figures in a result are determined by the original data and the operations performed. The final answers provided above reflect the appropriate number of significant figures based on the given information and the rules for significant figures.
For more such information on: significant figures
https://brainly.com/question/30169
#SPJ8
set s = 2z = {2x : x ∈ z}, the set of even integers. prove that s is equicardinal with z.
Answers
Consider the function f: Z → S defined as f(x) = 2x for every integer x ∈ Z. This function maps each integer to its corresponding even integer. For example, f(1) = 2, f(-1) = -2, and so on. To show that f is a bijection, we need to prove that it's both injective (one-to-one) and surjective (onto).
1. Injective: If f(x1) = f(x2), then 2x1 = 2x2. Dividing both sides by 2, we get x1 = x2. Thus, f is injective.
2. Surjective: For any even integer y ∈ S, there exists an integer x ∈ Z such that f(x) = y. Since y is even, y = 2x for some x ∈ Z. Thus, f(x) = 2x = y, and f is surjective.
To prove that set s, which is the set of even integers, is epicardial with set z, we need to show that there exists a one-to-one correspondence between the two sets.
We can define a function f: z → s as f(x) = 2x. This function maps each integer in z to its corresponding even integer in s.
To show that f is one-to-one, we need to show that if f(x) = f(y), then x = y. Suppose f(x) = f(y). This means that 2x = 2y, which implies that x = y. Therefore, f is one-to-one.
To show that f is onto, we need to show that for every element y in s, there exists an element x in z such that f(x) = y. Since y is an even integer, we can write it as y = 2x for some integer x. Therefore, f(x) = y, and f is onto.
Since f is one-to-one and onto, it is a bijection, which means that there exists a one-to-one correspondence between sets s and z. Therefore, s is epicardial with z.
Learn more about Function:
brainly.com/question/12431044
#SPJ11
moya picked 3 dozen apples she wents to share her apes in equal groups. show how many different way can she do this
Answers
Answer:
Groups of 12, Groups of 4, Groups of 6, Groups of 18
Step-by-step explanation:
12 x 3 = 36
36 splits evenly into 12, 4, 6, and 18 therefore that is your answer.
100 POINTS
Find the slope of the line passing through the points , −7−7 and , −36
i will make branlyst.
Answers
Answer:
The equation y = -0.24137931034483x – 8.6896551724138, assuming you meant (-36,0).
Step-by-step explanation:
What is the length of the hypotenuse of a triangle with vertices at(6,−9),(6,−10),and(10,−10)?
A. 10.82
B. 4.12
C. 3.61
D. 5.1
Answers
Answer:4.12
Step-by-step explanation: I need brainliest for next rank I’d appreciate it
According to Newton's Second Law, if two objects are pushed with the same force, which will accelerate
more, an object with more mass or an object with less mass?

Answers
Answer:
the one with more mass will accelorate less.
POSTING WHAT WASN'T ANSWERED PREVIOUSLY PLEASE ANSWER THESE
1. Let the market demand function for two companies namely, Coca-Cola and Pepsi be given by; Q(p) = 200 - P where Q = 9₁ +92. The cost function for each of the two firms in the industry is C(qi) = 2
Answers
The total Quantity demanded is:Q = 9 * (200 - P) + 92On simplifying this expression, we get:Q = 1828 - 9P
Substituting this value of Q in the profit function, we get:Pi = (198 - (1828 - 9P)) * qiOn
simplifying this expression, we get:Pi = (10P - 1630) * qi
This is the profit function for each firm in the industry.
The given market demand function for Coca-Cola and Pepsi is Q(p) = 200 - P. Here, Q denotes the total quantity demanded and P represents the price of the product.
The cost function for each of the two firms is C(qi) = 2q_i where q_i denotes the quantity produced by the ith firm.
Now, we need to determine the profit function for each firm in the industry.
To find out the profit function for each firm, we need to calculate the revenue function and subtract the cost function from it.The revenue function is the product of price and quantity. Therefore, the revenue function for both firms is:Ri = p * qi where Ri is the revenue of ith firm.
The price of each firm is determined by the market demand function as follows:p = 200 - QSubstituting this value of p in the above expression, we get:Ri = (200 - Q) * qi
Now, we need to calculate the profit function for each firm. It is given by the following expression:Pi = Ri - Ci where Pi is the profit of ith firm and Ci is the cost of production of ith firm. Substituting the value of Ri and Ci in the above equation, we get:
Pi = (200 - Q) * qi - 2qiOn simplifying this expression, we get:Pi = (198 - Q) * qiThis is the profit function for both firms in the industry. It is a function of quantity produced by each firm (qi) and total quantity demanded (Q). Hence, the profit of each firm depends on the total quantity demanded and the quantity produced by the firm.
The given demand function is Q(p) = 200 - P. Here, we are given Q = 9₁ + 92.
Therefore, the total quantity demanded is:Q = 9 * (200 - P) + 92On simplifying this expression, we get:Q = 1828 - 9P
Substituting this value of Q in the profit function, we get:Pi = (198 - (1828 - 9P)) * qiOn
simplifying this expression, we get:Pi = (10P - 1630) * qi
This is the profit function for each firm in the industry.
For more questions on Quantity .
https://brainly.com/question/29181693
#SPJ8
a band just recorded a new album with 13 tracks. the shortest song on the album is 1 minute and 14 seconds. The longest song is 5 minutes and 54 seconds. What is a reasonable estimate for the total time of the album?
Answers
To find a reasonable estimate for the total time of the album, we can add the times of the shortest and longest songs and divide by 2 to find the average time per song, and then multiply by the total number of songs on the album.
What is a reasonable estimate for the total time of the album?The shortest song on the album is 1 minute and 14 seconds, which is equivalent to 74 seconds.
The longest song on the album is 5 minutes and 54 seconds, which is equivalent to 354 seconds.
Therefore, the average time per song is:
(74 + 354) / 2 = 214 seconds
And the total time of the album is approximately:
13 songs x 214 seconds/song = 2,782 seconds
Converting this to minutes and seconds, we get:
2,782 seconds = 46 minutes and 22 seconds
So a reasonable estimate for the total time of the album is about 46 minutes and 22 seconds.
Learn more about time from
https://brainly.com/question/15418098
#SPJ1
Find the product of 4^2 x 3 ^6
Answers
Answer: 11664
I think
Answer:
11,664
Step-by-step explanation:
4^2 x 3^6
16 x 729
11,664
Solve the equation
3x-2
4
-
2x - 5- 1 + x
3 6

Answers
Answer:
\(\boxed{\sf x=12}\)Step-by-step explanation:
\(\sf \cfrac{3x-2}{4}-\cfrac{2x-5}{3}=\cfrac{1+x}{6}\)
First, let's find the LCM of 4, 3, and 6.
How to find the LCM:
→ List multiples of each number.
→ Find the smallest number on each list.
4: 4, 8, 12, 16, 20, 24..
3: 3, 6, 9, 12, 15, 18, 21, 24, 27....
6: 6, 12, 18, 24, 30, 36, 42...
LCM: 12
_________
Now, we'll Multiply by LCM:
\(\sf \cfrac{3x-2}{4}\times \:12-\cfrac{2x-5}{3}\times \:12=\cfrac{1+x}{6}\times \:12\)
Simplify:
\(\sf 3\left(3x-2\right)-4\left(2x-5\right)=2\left(x+1\right)\)
Now, expand, Apply the Distributive property:
\(\bold{ 3\left(3x-2\right)-4\left(2x-5\right)}\)
\(\sf 9x-6-8x+20\)
Combine like terms:
\(\sf x+14\)
________
\(\bold{ 2\left(x+1\right)}\)
\(\sf 2x+2\)
\(\sf x+14=2x+2\)
Subtract 14 from both sides:
\(\sf x+14-14=2x+2-14\)
Simplify:
\(\sf x=2x-12\)
Subtract 2x from both sides:
\(\sf x-2x=2x-12-2x\)
Simplify:
\(\sf -x=-12\)
Divide both sides by -1:
\(\sf \cfrac{-x}{-1}=\cfrac{-12}{-1}\)
\(\sf x=12\)
____________________________Rent expense in Volusia Company's 2014 income statement is $420,000. If Prepaid Rent was $70,000 at December 31, 2013, and is $95,000 at December 31, 2014, the cash paid for rent during 2014 is:A. $480,000B. $445,000C. $395,000D. $420,000
Answers
As per the mentioned informations, the cash paid for rent during 2014 is calculated to be $395,000. So, the correct answer is option (C) i.e. $395,000.
To calculate the cash paid for rent during 2014, we need to use the information given in the problem and apply the following formula:
Cash paid for rent = Rent expense + Prepaid rent at the beginning of the period - Prepaid rent at the end of the period
Substituting the values given in the problem, we get:
Cash paid for rent = $420,000 + $70,000 - $95,000
Cash paid for rent = $395,000
Therefore, it can be concluded that the correct answer is (C) $395,000.
Learn more about Cash :
https://brainly.com/question/13226199
#SPJ4
How many square feet of cement would be needed for a 7-foot wide continual sidewalk around the OUTSIDE EDGE of a 60 foot by 90 foot corner lot? Side A is 60' long and Side B is 90' long. A 1,050 square feet B 1,099 square feet C 420 square feet D 630 square feet
Answers
The amount of square feet of cement needed for the sidewalk is 1,050 square feet.
To calculate the square footage of the cement needed for the sidewalk around the outside edge of the lot, we need to find the perimeter of the lot and then subtract the inner area.
The perimeter of the lot can be calculated by adding up all four sides:
Perimeter = Side A + Side B + Side A + Side B
Perimeter = 60 + 90 + 60 + 90
Perimeter = 300 feet
Since the sidewalk is 7 feet wide and runs along the outside edge of the lot, we need to subtract the area of the inner rectangle (60 feet by 90 feet) from the area of the outer rectangle (74 feet by 104 feet) to find the area of the sidewalk.
Area of the outer rectangle = 74 * 104
= 7,696 square feet
Area of the inner rectangle = 60 * 90
= 5,400 square feet
Area of the sidewalk = Area of the outer rectangle - Area of the inner rectangle
Area of the sidewalk = 7,696 - 5,400
Area of the sidewalk = 2,296 square feet
To know more about amount,
https://brainly.com/question/29659440
#SPJ11
Show that the following equations have at least one solution on the given interval:
xcosx - 2x^2 + 3x - 1 = 0 on [1.2, 1.3]
x - (lnx)^x = 0 over [4, 5]
Answers
Main Answer:The equations :xcosx - 2x^2 + 3x - 1 = 0 on [1.2, 1.3]
x - (lnx)^x = 0 over [4, 5] have at least one solution on the given interval.
Supporting Question and Answer:
What is the Intermediate Value Theorem?
The Intermediate Value Theorem states that if a function is continuous on a closed interval and takes on values of opposite signs at the endpoints of the interval, then it must have at least one root (or solution) within that interval.
Body of the Solution:To show that the equations have at least one solution on the given intervals, we can use the Intermediate Value Theorem. According to the theorem, if a function is continuous on a closed interval and takes on values of opposite signs at the endpoints of the interval, then it must have at least one root within that interval.
Let's analyze each equation separately:
xcosx - 2x^2 + 3x - 1 = 0 on [1.2, 1.3]
To apply the Intermediate Value Theorem, we need to show that the function is continuous on the interval and takes on values of opposite signs at the endpoints.
First, let's check the continuity of the function. Both xcosx and -2x^2 + 3x - 1 are continuous functions on their respective domains. Thus, their sum, xcosx - 2x^2 + 3x - 1, is also continuous on the interval [1.2, 1.3].
Next, we evaluate the function at the endpoints:
f(1.2) = (1.2)cos(1.2) - 2(1.2)^2 + 3(1.2) - 1
≈ 0.0317
f(1.3) = (1.3)cos(1.3) - 2(1.3)^2 + 3(1.3) - 1
≈ -0.0735
Since f(1.2) is positive and f(1.3) is negative, the function changes sign within the interval [1.2, 1.3]. Therefore, by the Intermediate Value Theorem, the equation xcosx - 2x^2 + 3x - 1 = 0 has at least one solution within the interval [1.2, 1.3].
x - (lnx)^x = 0 over [4, 5]
Again, we need to verify the continuity of the function and the sign change at the endpoints.
The function x - (lnx)^x is continuous on the interval [4, 5], as both x and lnx are continuous functions on their respective domains.
Evaluating the function at the endpoints:
f(4) = 4 - (ln4)^4
≈ -3.9616
f(5) = 5 - (ln5)^5
≈ 3.0342
Since f(4) is negative and f(5) is positive, the function changes sign within the interval [4, 5]. By the Intermediate Value Theorem, the equation x - (lnx)^x = 0 has at least one solution within the interval [4, 5].
Final Answer:In both cases, we have shown that the equations have at least one solution within the given intervals using the Intermediate Value Theorem.
To learn more about the Intermediate Value Theorem from the given link
https://brainly.com/question/30557318
#SPJ4
The equations :xcosx - 2x² + 3x - 1 = 0 on [1.2, 1.3]
x - (lnx)^x = 0 over [4, 5] have at least one solution on the given interval.
What is the Intermediate Value Theorem?The Intermediate Value Theorem states that if a function is continuous on a closed interval and takes on values of opposite signs at the endpoints of the interval, then it must have at least one root (or solution) within that interval.
To show that the equations have at least one solution on the given intervals, we can use the Intermediate Value Theorem. According to the theorem, if a function is continuous on a closed interval and takes on values of opposite signs at the endpoints of the interval, then it must have at least one root within that interval.
Let's analyze each equation separately:
xcosx - 2x² + 3x - 1 = 0 on [1.2, 1.3]
To apply the Intermediate Value Theorem, we need to show that the function is continuous on the interval and takes on values of opposite signs at the endpoints.
First, let's check the continuity of the function. Both xcosx and -2x² + 3x - 1 are continuous functions on their respective domains. Thus, their sum, xcosx - 2x² + 3x - 1, is also continuous on the interval [1.2, 1.3].
Next, we evaluate the function at the endpoints:
f(1.2) = (1.2)cos(1.2) - 2(1.2)² + 3(1.2) - 1
≈ 0.0317
f(1.3) = (1.3)cos(1.3) - 2(1.3)² + 3(1.3) - 1
≈ -0.0735
Since f(1.2) is positive and f(1.3) is negative, the function changes sign within the interval [1.2, 1.3]. Therefore, by the Intermediate Value Theorem, the equation xcosx - 2x² + 3x - 1 = 0 has at least one solution within the interval [1.2, 1.3].
x - (lnx)ˣ = 0 over [4, 5]
Again, we need to verify the continuity of the function and the sign change at the endpoints.
The function x - (lnx)ˣ is continuous on the interval [4, 5], as both x and lnx are continuous functions on their respective domains.
Evaluating the function at the endpoints:
f(4) = 4 - (ln4)⁴
≈ -3.9616
f(5) = 5 - (ln5)⁵
≈ 3.0342
Since f(4) is negative and f(5) is positive, the function changes sign within the interval [4, 5]. By the Intermediate Value Theorem, the equation x - (lnx)^x = 0 has at least one solution within the interval [4, 5].
In both cases, we have shown that the equations have at least one solution within the given intervals using the Intermediate Value Theorem.
To learn more about the Intermediate Value Theorem
brainly.com/question/30557318
#SPJ4
8. Write an equation of the line perpendicular to y = x + 4 that contains (3,-3). Please write the
equation in point-slope form.
Answers
Answer:
y + 3 = - (x - 3)
Step-by-step explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
y = x + 4 ← is in slope- intercept form
with slope m = 1
given a line with slope m then the slope of a line perpendicular to it is
\(m_{perpendicular}\) = - \(\frac{1}{m}\) = - \(\frac{1}{1}\) = - 1
the equation of a line in point- slope form is
y - b = m(x - a)
where m is the slope and (a, b ) a point on the line
here m = - 1 and (a, b ) = (3, - 3 ) , then
y - (- 3) = - 1 (x - 3) , that is
y + 3 = - (x - 3)
HELP ME
A 6-foot tall man has a 9-foot shadow. At the same time, a tree he is standing next to has a 30-foot shadow.
A. 20 ft
B. 27 ft
C. 45 ft
D. 21 ft
E. 24 ft
Answers
Answer:
A.20 ft
Step-by-step explanation:
the shadow is double the height of the object.
Please help asap ty !!
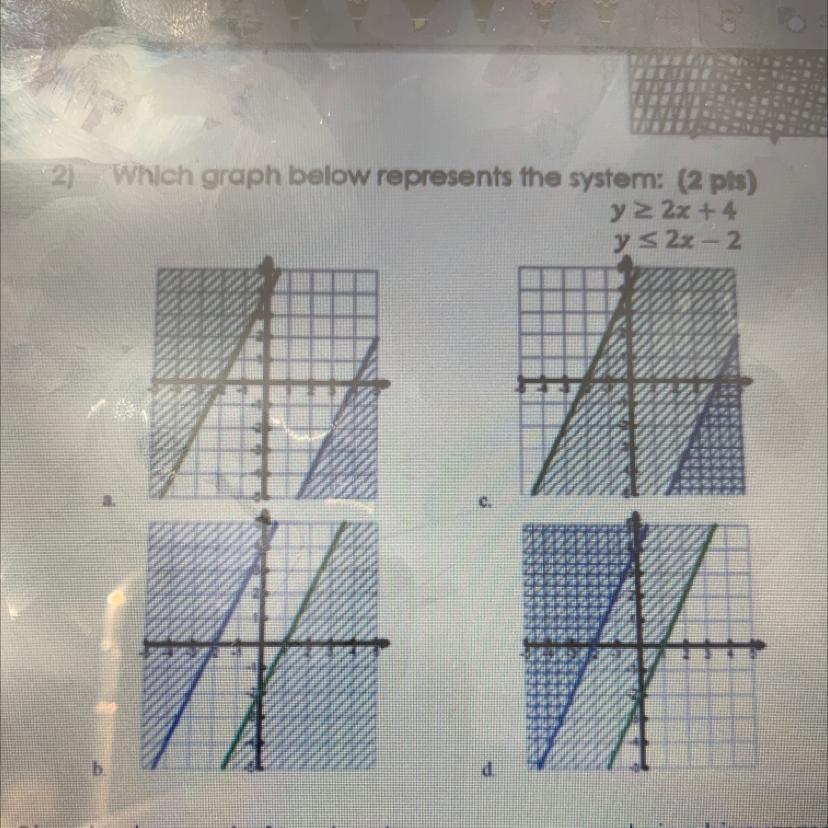
Answers
Answer:
B
Step-by-step explanation:
Answer:
The Graph located as B.
Step-by-step explanation:
:) Thank you i have done this before! I hope you have a great life?!
Thanks so much! Byes!
10. Walter drives 7 mph over the speed limit on a suburban street. In the time that Walter drives 4 miles, a car driving the posted speed limit could drive \( 31 / 3 \) miles. What is the speed limit
Answers
The speed limit on the suburban street is approximately 11.42 mph.
Let's assume the speed limit on the suburban street is x mph.
Walter drives 7 mph over the speed limit, so his speed is (x + 7) mph.
In the time it takes Walter to drive 4 miles, a car driving the posted speed limit could drive
31
3
3
31
miles.
We can set up the following equation to represent the relationship between time, speed, and distance:
Time = Distance / Speed
For Walter: Time = 4 miles / (x + 7) mph
For the car driving the speed limit: Time =
31
3
3
31
miles / x mph
Since the times are equal, we can equate the two expressions:
4 / (x + 7) =
31
3
3
31
/ x
To solve for x, we can cross-multiply and simplify:
4x =
31
3
3
31
* (x + 7)
12x = 31(x + 7)
12x = 31x + 217
31x - 12x = 217
19x = 217
x = 217 / 19
x ≈ 11.42
Know more about speed limit here;
https://brainly.com/question/10492698
#SPJ11
The width of a rectangle is 5 feet less than the length. The perimeter is 62. Find the length and width of the rectangle.
Variables: ___________________________
Model equation: ______________________________
Length of the rectangle: ______________________________
Width of the rectangle: ______________________________
Answers
Perimeter formula: p = 2(w + l)
The perimeter is 62.
p = 62
The width of a rectangle is 5 feet less than the length.
w = l - 5
Substitute and solve.
62 = 2[(l - 5) + l)]
62 = 2l + 2l - 10
62 = 4l - 10
72 = 4l
18 = l
Substitute and solve for the width
w = 18 - 5
w = 13
Therefore, the length is 18 and the width is 13.
Best of Luck!
Answer:
see below and attached.
Step-by-step explanation:
Perimeter (P) = 2 L (Length) + 2 W (Width)
where P = 62
W = L - 5
P = 2L + 2W
62 = 2L + 2(L -5)
62 = 2L + 2L - 10
72 = 4L
L = 72/4
L = 18
W = L - 5
W = 18 - 5
W = 15
Variables : P, L, W
Model equation: P = 2L + 2W
Length of the rectangle: 18
Width of the rectangle: 13

there are three highways in the county. the number of daily accidents that occur on these highways are poisson random variables with respective parameters . 3, . 5, and . 7 . find the expected number of accidents that will happen on any of these highways today.
Answers
There are three highways in the county. the number of daily accidents that occur on these highways are poison random variables with respective parameters . 3, . 5, and . 7 The expected number of accidents that will happen on any of these highways today is 1.5
There is a theorem that we can use to find the expected value of a random variable that is a sum of other random variables as follows.
If X= X₁ + X₂ +...... +Xₓ, then E( X)= E(X₁) +E( X₂) +...... +E(Xₓ),
In this case, let X = the number of accidents that will happen on any of those highways today,
are the numbers of accidents on each highway, respectively.
Then X= X₁ + X₂ +X₃ .
Since are Poisson variates, their expected values are the parameters given, .3, .5 and .7.
So E(X₁) = .3 E( X₂) = .5 E(X₃)= .7
Thus, E(X)= 1.5
A similar Poisson random variable problem is given at
https://brainly.com/question/28799409
#SPJ4
What is 105 kg to lbs?
Answers
105 kg to lbs is 231.485375 Pounds. To convert 105 kilograms to pounds, multiply that number by 2.205.
The International Prototype of the Kilogram (IPK), a block of platinum-iridium alloy created in 1889 and stored at the International Bureau of Weights and Measures in Sèvres, France, serves as the reference point for determining what a kilogram (kg) is equal to in terms of mass. It is the only SI unit that is determined by a physical feature that can be recreated in a lab rather than an actual thing. 1000g (grams) equals one kilogram. In the imperial system of mass measurement, the pound is a weight unit that is frequently used to denote mass.
Here is more information about kilograms: brainly.com/question/28844288
#SPJ4