A sample of the reading scores of 35 fifth-grade students has a mean of 82. The standard deviation of the sample is 15.
Requried:
a. Find the 95%% confidence interval of the true mean reading score for all fifth graders.
b. Find the 95% confidence interval of the mean reading scores of all fifth graders
c. find the 99% confidence interval of the mean reading scores of fifth graders
s. Which interval is larger? explain why?
Answers
a. 95% confidence Interval of the True Mean Reading Score for All Fifth Graders: (76.85, 87.15)
b. 95% Confidence Interval of the Mean Reading Scores of All Fifth Graders: (77.03, 86.97)
c. 99% Confidence Interval of the Mean Reading Scores of Fifth Graders:(75.85, 88.15)
s. The 99% confidence interval is wider than the 95% confidence intervals because a higher confidence level requires a larger margin of error and a wider interval to capture the true mean with a higher degree of certainty.
To find the confidence intervals, we'll use the formula:
Confidence Interval = Mean ± (Critical Value × Standard Error)
Where:
Mean is the sample mean
Critical Value is the value corresponding to the desired confidence level and degrees of freedom
Standard Error is the standard deviation of the sample divided by the square root of the sample size
a. 95% Confidence Interval of the True Mean Reading Score for All Fifth Graders:
Since the sample size is 35, the degrees of freedom (df) will be 35 - 1 = 34.
The critical value for a 95% confidence level and 34 degrees of freedom is approximately 2.032.
Standard Error (SE) = Standard Deviation (SD) / √n
SE = 15 / √35 = 2.533
= 82 ± 5.15
= (76.85, 87.15)
b. 95% Confidence Interval of the Mean Reading Scores of All Fifth Graders:
We consider the standard error as the standard deviation of the population divided by the square root of the sample size.
Confidence Interval = 82 ± (2.032 × (15 / √35))
= 82 ± 4.97
= (77.03, 86.97)
c. 99% Confidence Interval of the Mean Reading Scores of Fifth Graders:
The critical value for a 99% confidence level and 34 degrees of freedom is approximately 2.728.
Confidence Interval = 82 ± (2.728 × (15 / √35))
=82 ± 6.15
= (75.85, 88.15)
s. Comparing the Intervals:
The 99% confidence interval is larger than the 95% confidence intervals (both for the true mean reading score and the mean reading scores of all fifth graders).
Because a higher confidence level requires a wider interval to capture the true mean with a higher degree of certainty.
As the confidence level increases, the critical value increases, resulting in a larger margin of error and a wider confidence interval.
To learn more on Statistics click:
https://brainly.com/question/30218856
#SPJ4
Related Questions
Determine which consecutive integers do not have a real zero of f(x) = x3 - 4x2 - 4x+ 15 between them. a (4, 5) c. (2-1) b. (1, 2) d (-3,-2)
Answers
Answer: B
Step-by-step explanation: the answer is (0,1)
please help (AP Calc AB) will mark brainliest! image provided

Answers
Answer:
So I think your answer is Zero
I think it will help you.
I NEEED HELLLPP EASYYYYYYY
Answers
Answer:
With what!
Step-by-step explanation:
Answer:
66.666666666667%
Step-by-step explanation:
Which equation represents a line that passes through the two points in the
table?

Answers
Answer:
A. y-1=5/3(x-3)
Step-by-step explanation:
please look at the graph in my pic to see my answer is correct
hope it helps :)

please help me with these two questions

Answers
number 7 is B, number 8 is D.
Yo can yall answer this for me??

Answers
8 ÷ 640 x 100,000 = 12,500 defective computer chips
Scaling calculationWe can anticipate that a larger sample of 100,000 chips will exhibit the same rate of defects if the sample of 640 chips produced 8 defective ones.As a result, 8/640 Equals x/100,000, where x is the quantity of flawed chips. x = 8000 can be used to sum up this. As a result, we may anticipate that out of every 100,000 computer chips produced, there will be about 8,000 that are flawed.However, this presupposes that the defect rate stays constant and that the 640 chip sample is typical of the 100,000 chip population as a whole.Additionally, when the overall number of chips manufactured rises, the defect rate could either rise or fall.To ensure accuracy and reliability of this prediction, it is important to collect more data from larger sample sizes.To learn more about scaling calculation refer to:
https://brainly.com/question/2826496
#SPJ1
what is the distance from the point (12, 14, 1) to the y-z plane?
Answers
The problem involves finding the distance from a given point (12, 14, 1) to the y-z plane. The distance can be determined by finding the perpendicular distance from the point to the plane.
The equation of the y-z plane is x = 0, as it does not depend on the x-coordinate. We need to calculate the perpendicular distance between the point and the plane.
To find the distance from the point (12, 14, 1) to the y-z plane, we can use the formula for the distance between a point and a plane. The formula states that the distance d from a point (x₀, y₀, z₀) to a plane Ax + By + Cz + D = 0 is given by the formula:
d = |Ax₀ + By₀ + Cz₀ + D| / √(A² + B² + C²)
In this case, since the equation of the y-z plane is x = 0, the values of A, B, C, and D are 1, 0, 0, and 0 respectively. Substituting these values into the formula, we can calculate the distance from the point to the y-z plane.
To know more about distances click here: brainly.com/question/31713805
#SPJ11
22 The five-number summary for scores on a statistics exam is: 35, 68, 77, 83 and 97. In all, 196 students took this exam About how many students had scores between 68 and 83? a. 98 b. 39 c. 6
d. 148 e.49
Answers
The approximate number of students with Scores between 68 and 83 is 98.Answer: a. 98
The five-number summary for scores on a statistics exam is: 35, 68, 77, 83 and 97. In all, 196 students took this exam About how many students had scores between 68 and 83?
The five-number summary consists of the minimum value, the first quartile, the median, the third quartile, and the maximum value.
The interquartile range is the difference between the third and first quartiles. Interquartile range (IQR) = Q3 – Q1, where Q3 is the third quartile and Q1 is the first quartile. The 5-number summary for scores on a statistics exam is given below:
Minimum value = 35
First quartile Q1 = 68
Median = 77
Third quartile Q3 = 83
Maximum value = 97
The interval 68–83 is the range between Q1 and Q3.
Thus, it is the interquartile range.
The interquartile range is calculated as follows:IQR = Q3 – Q1 = 83 – 68 = 15
The interquartile range of the scores between 68 and 83 is 15. Therefore, the number of students with scores between 68 and 83 is roughly half of the total number of students. 196/2 = 98.
Thus, the approximate number of students with scores between 68 and 83 is 98.Answer: a. 98
For more questions on Scores .
https://brainly.com/question/32698527
#SPJ8
example 2 major premise: no dogmatists are scholars who encourage free thinking. minor premise: some theologians are scholars who encourage free thinking. conclusion: some theologians are not dogmatists. the major premise in example 2 is an proposition. the minor premise in example 2 is an proposition. the conclusion in example 2 is an proposition. therefore, the mood of the categorical syllogism in example 2 is .
Answers
The mood of the categorical syllogism in example 2 is AIO.
In your example, we have the following premises and conclusion:
1. Major Premise: No dogmatists are scholars who encourage free thinking.
2. Minor Premise: Some theologians are scholars who encourage free thinking.
3. Conclusion: Some theologians are not dogmatists.
The major premise in example 2 is an A proposition (All S are not P). The minor premise in example 2 is an I proposition (Some S are P). The conclusion in example 2 is an O proposition (Some S are not P).
To learn more about premises, refer here:
https://brainly.com/question/29699382#
#SPJ11
The measure of one acute angle of a right triangle is 6 less than twice the measure of the other acute angle. Find the measure of each acute angle.
Answers
The measure of each of the acute angles of the right triangle is 32° and 58°.
A right triangle is a kind of triangle which has a right angle (90°) and two acute angles (less than 90°).
Let x = measure of one of the acute angles
If the measure of one acute angle of a right triangle is 6 less than twice the measure of the other acute angle, then
measure of the other acute angle = 2x - 6
The sum of all the angles of any triangle is equal to 180°. Hence,
90° + x + 2x - 6 = 180°
Solve for the value of x.
3x = 96
x = 32
Solve for the measure of the other acute angle.
2x - 6 = 2(32) - 6 = 58
Hence, the two angles are 32° and 58°.
Learn more about right triangles here: https://brainly.com/question/1635412
#SPJ4
How does the graph of g(x) = (x − 8)3 + 3 compare to the parent function f(x) = x3?
a. g(x) is shifted 8 units to the left and 3 units up.
b. g(x) is shifted 3 units to the right and 8 units down.
c. g(x) is shifted 8 units to the right and 3 units up.
d. g(x) is shifted 3 units to the right and 8 units up.
Answers
Answer:
The right answer is C.
Step-by-step explanation:
The parent function is:
\(f(x)=x^3\)
If something is subtracted from variable \(x\) it means the graph shifted toward right and something is added to \(y\) value then the graph is shifted up.
\(f(x)=(x-8)^3\)
graph shifted toward right by \(8\) units right
\(f(x)=(x-8)^3+3\)
graph shifted toward right by \(3\) units up
Thus the new function is:
\(g(x)=(x-8)^3+3\)
1.) a.) Given the data representing test scores in a chemistry class, construct a grouped frequency distribution of
the data using classes 30-40, 40-50, and so on using the grid provided.
72
55
35
53
85
67
48
86
39
73
57
99
45
48
40
80
Classes
70
56
59
75
85
97
65
62
66
88
94
74
Frequency
92
74
98
81
100 87
76
89
84
73
85
80
Answers
Given statement solution is :- To construct a grouped frequency distribution for the given test scores data, we will use the provided classes: 30-40, 40-50, and so on. Here's the grouped frequency distribution:
Classes Frequency
30-40 2
40-50 3
50-60 4
60-70 8
70-80 9
80-90 7
90-100 7
To construct a grouped frequency distribution for the given test scores data, we will use the provided classes: 30-40, 40-50, and so on. Here's the grouped frequency distribution:
Classes Frequency
30-40 2
40-50 3
50-60 4
60-70 8
70-80 9
80-90 7
90-100 7
To create this distribution, we count the number of scores that fall within each class range. For example, the class 30-40 has 2 scores falling within that range (35 and 39), and the class 40-50 has 3 scores (45, 48, and 48).
Note: It seems there is an inconsistency in the data provided. The class range 70-80 has 9 scores, but the frequencies given for the other classes do not match the actual number of scores falling within those ranges. Therefore, I have used the actual counts from the data to construct the grouped frequency distribution.
For such more questions on Grouped Frequency Distribution
https://brainly.com/question/29115601
#SPJ8
a dolphin pool has a circumference of 38m. what is the area, to the nearest meter?
Answers
Answer:
hsjdnbd dmkdjnf
Step-by-step explanation:
atep by step
A train traveling at a speed of 160 km / hr will take 18 hours to cover between two cities . How long will it take a car travelling at 120 km/hr to cover the same distance
Answers
Answer:
24 hours
Step-by-step explanation:
160 x 18 = 2880
2880/120 = 24
what is the answer to this polynomial (5x-2)^2?
Answers
Answer:
Answer and Explanation: Given polynomial expression is: (5x2+3x−5)−(x2 −6x−4) ( 5 x 2 + 3 x − 5) − ( x 2 − 6 x − 4).
Step-by-step explanation:
Answer:
25x^2 -20x +4
Step-by-step explanation:
(5x-2)^2
FOIL
(5x-2)(5x-2)
25x^2 -10x -10x +4
25x^2 -20x +4
Round 771 to the nearest hundred
Answers
Answer:
800
Step-by-step explanation:
700________________750___________771________800
771 is over 750 so it would be rounded to 800
Answer: 800
Step-by-step explanation:
771 is 50+ thus it round over to 800.
There are 10 rulers, 6 erasers, and 8 red pens. Write the ratio for earaser to rulers in simplest
Answers
Answer:
The answer to the question is 5:3:4
Huang graphed (x – 1)2 > –2(y – 4). Which reasons could Huang use to justify that his graph is correct? Check all that apply. Because only the x quantity is squared, the curve is a parabola. The values subtracted from x and y in the equation are the coordinates of the vertex which is (1, 4). The parabola opens left because –2 is in front of the y-quantity. The shading is outside the parabola because (0, 0) doesn’t satisfy the inequality. There is a strict inequality so they boundary is not included in the solution set.
Answers
Answer:
1,2,4, & 5
Step-by-step explanation:
Got it right on Edge 2021
Answer:
A, B, D, and E
Step-by-step explanation:
Edge 2021
Expand and simplify the following. Show all the steps.
a. -4(a-4)
b. 3a(a+2)
c. 4x - 2(5 - x)
d (x-3)(x+2)
e (x+4)2
Answers
b) 3a^2+6a
c) 20x - 4x^2- 10 + 2x
-4x^2 + 22x -10
d) x^2+2x-3x-6
x^2-x-6
e) (x+4)(x+4)
x^2+8x+16
a. The expanded and simplified form is: -4a + 16
b. The expanded and simplified form is: 3a^2 + 6a
c. The expanded and simplified form is: 6x - 10
d. The expanded and simplified form is: x^2 - x - 6
e. The expanded and simplified form is: x^2 + 8x + 16
Sure, let's expand and simplify each expression step by step:
a. -4(a - 4)
Step 1: Apply the distributive property (multiply -4 by each term inside the parentheses).
-4(a) + -4(-4)
Step 2: Simplify the terms.
-4a + 16
So, the expanded and simplified form is: -4a + 16
b. 3a(a + 2)
Step 1: Apply the distributive property (multiply 3a by each term inside the parentheses).
3a * a + 3a * 2
Step 2: Simplify the terms.
3a^2 + 6a
So, the expanded and simplified form is: 3a^2 + 6a
c. 4x - 2(5 - x)
Step 1: Apply the distributive property (multiply -2 by each term inside the parentheses).
4x - 2 * 5 + 2 * x
Step 2: Simplify the terms.
4x - 10 + 2x
Step 3: Combine like terms.
6x - 10
So, the expanded and simplified form is: 6x - 10
d. (x - 3)(x + 2)
Step 1: Apply the distributive property (multiply x by each term inside the second parentheses and then multiply -3 by each term inside the second parentheses).
x * x + x * 2 - 3 * x - 3 * 2
Step 2: Simplify the terms.
x^2 + 2x - 3x - 6
Step 3: Combine like terms.
x^2 - x - 6
So, the expanded and simplified form is: x^2 - x - 6
e. (x + 4)^2
Step 1: Apply the square of a binomial formula: (a + b)^2 = a^2 + 2ab + b^2
(x)^2 + 2(x)(4) + (4)^2
Step 2: Simplify the terms.
x^2 + 8x + 16
So, the expanded and simplified form is: x^2 + 8x + 16
To know more about simplify:
https://brainly.com/question/17579585
#SPJ2
Neil rents a bike that costs $12 for 4 hours and $18 for 7 hours. Whats the slope?
Answers
Answer: 2
Step-by-step explanation:The slope of a line is the ratio of the change in y-values to the change in x-values between two points on the line.
To find the slope, we first need to find two points on the line, for example (4,12) and (7,18).
Then, the slope can be calculated as:
(18 - 12) / (7 - 4) = 6 / 3 = 2.
The slope is 2.
Of the pies that Lorenzo's Pie Shop sold last month, 1/2 were blueberry pies and 2/5 were blackberry pies. What fraction of the pies sold were either blueberry or blackberry?
Answers
Then the answer is 9/10
This problem involves adding fractions with different denominators. For this type of problem you can change the value of the denominators in each fraction to equal the same thing. Since they are fractions, the overall value will not change if you multiply the numerator and denominator by the same number.
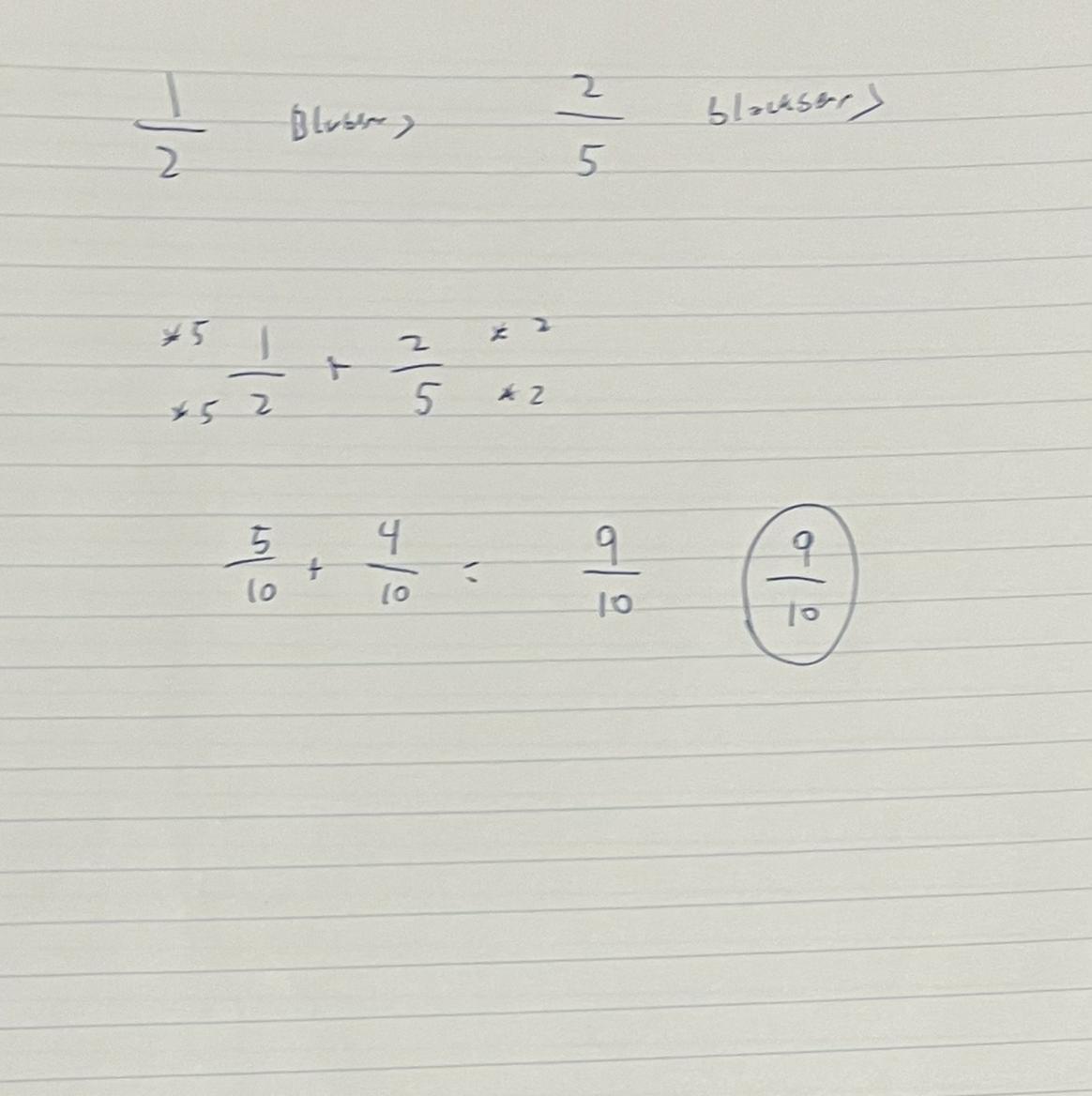
Mark me as brainliest plsssss
Hope I help
3) -7x - 3x + 2 = -8x - 8
Answers
-10x+2=-8x-8
-10x+8x+2=-8
-2x+2= -8
-2x = -8 + 2
-2x= -6
X= -6/-2
X= 3
I'd appreciate a thorough and clear step-by-step explanation with a proper picture. Thank you in advance!
Show transcribed data
Assume you have a position sensor with a transfer function H(s) 1 = S+1 Use a proportional (P) controller to control the position of the carriage x(t) when f(t) = 0. Find the value of the controller gain KP that makes the system marginally stable. Also find the poles of the system at this X(S) condition. Transfer Function of Plant: V(s) 53 +10.592 +555 10
Answers
A proportional (P) controller is used to regulate the position of the carriage x(t) when f(t) = 0, provided that a position sensor with a transfer function H(s) = S + 1 is available.
The transfer function of the plant is given by:
`V(s)/X(s) = 53s^2 + 10.592s + 555`We must first determine the closed-loop transfer function T(s).T(s) = H(s) G(s) / [1 + H(s) G(s)]
where G(s) = KP is the transfer function of the proportional controller.Hence, T(s) = KP (S + 1) / [KP (S + 1) + 53 S^2 + 10.592 S + 555]At s = jω (where j = sqrt(-1)), the magnitude of T(s) is given by:
|T(jω)| = K / √[(ω^4 + 107.184ω^2 + 2915.025) + (KPω^3 + 53ω^2 + 10.592ω + KP) ^2]Let's choose KP such that the system is marginally stable, that is, the closed-loop transfer function T(s) has a unit gain margin, i.e.|T(jω)| = 1, or|T(jω)|^2 = 1
From the above equation, we can calculate the value of KP that produces the unit gain margin for the given system. Substituting the above equation, we get:
KP^2 ω^6 + KPω^3 (53 - 1) + ω^4 + 107.184ω^2 + 2915.025 = 0
We are interested in finding the value of KP such that the root of the above polynomial has a multiplicity of two at s = jω, i.e. it is a double root or pole of the closed-loop system. By setting Δ = b^2 - 4ac = 0, we obtain the quadratic equation in KPω^3,0 = (52)^2 - 4 (1) (ω^4 + 107.184ω^2 + 2915.025)
Therefore, ω = 8.201 rad/sKP = 1.93
From the transfer function of the closed-loop system, we can now find the value of the pole(s).The characteristic polynomial of the closed-loop system is:
P(s) = KP (S + 1) + 53 S^2 + 10.592 S + 555By substituting KP = 1.93 in P(s), we obtain:
P(s) = 1.93 (S + 1) + 53 S^2 + 10.592 S + 555
This can be factored to obtain the poles of the system:
P(s) = (S + 11.18) (S + 0.132)
The poles of the system are -11.18 and -0.132.
To know more about polynomial visit:
https://brainly.com/question/11536910
#SPJ11
an oil company purchased an option on land in alaska. preliminary geologic studies assigned the following prior probabilities. What is the probability of finding oil?
Answers
If an oil company purchased an option on land in alaska with probabilities P(high - quality oil) = 0.5, P(medium quality oil) = 0.20 and P(no oil) = 0.30 , the probability of finding oil is 0.7, or 70%.
The probability of finding oil can be calculated by adding the probabilities of finding high-quality oil and medium-quality oil, as they are the only two scenarios in which oil is present. Therefore, the probability of finding oil is:
P(oil) = P(high-quality oil) + P(medium-quality oil)
P(oil) = 0.5 + 0.20
P(oil) = 0.7
There there is 0.7 or 70% probability that the oil is found in alaska using these given probabilities.
To learn more about probability click on,
https://brainly.com/question/30807592
#SPJ4
Complete question is:
An oil company purchased an option on land in alaska. preliminary geologic studies assigned the following prior probabilities.
P(high - quality oil) = 0.5 ,P(medium quality oil) = 0.20 ,P(no oil) = 0.30
What is the probability of finding oil?
What would an equation be for a line with a slope of 3 and a y-intercept of 7?

Answers
Answer:
y = 3x + 7
Step-by-step explanation:
Using the formula y = mx + b we can create this equation.
m = slope
b = y -intercept
based on the information provided I know that
Slope = 3
and
y-intercept = 7
Substitute:
y = mx + b
y = 3x + 7
y = 3x + 7 is the equation when the slope is 3 and the y intercept is 7.
Let us use the slope-intercept form for this, with m as the slope and b as a constant.
y = mx + b
7 = 3(0) + b [since the y-int is 7, the x value will be zero]
b = 7
y = 3x + 7
Pleaseeeeee helpppppp!
I will mark brainliest, but pls only if you know the answer
Its Geometry A

Answers
Answer:
see explanation
Step-by-step explanation:
A base angle
B leg
C vertex angle
D leg
E base angle
F base
in any isosceles triangle there are 2 congruent legs and 2 congruent base angles.
the base angles are opposite the congruent legs
the remaining side, the base is the 3rd side of the triangle
the vertex angle is formed by the 2 congruent legs
Which is the correct answer?

Answers
Answer:
a reflection in the y axis followed by a translation 1 unit down
Step-by-step explanation:
Reflection over the y-axis then a unit down
Chicago and Atlanta are cities with two of the busiest airports in the United States.
Unfortunately, both of these cities have frequent thunderstorms and other weather
problems that lead to flight delays. Henry flies frequently to both cities and suspects
that Chicago has a higher proportion of delayed flights. In two independent, random
samples he finds that Chicago has 37 out 119 flights were delayed, while Atlanta has
only 25 delayed flights out of 127 sampled flights. Is there statistically significant
evidence that the proportion of delayed flights from Chicago is higher than the
proportion of delayed flights from Atlanta? Use a = 0. 5.
Answers
There is statistically significant evidence to suggest that the proportion of delayed flights from Chicago is higher than the proportion of delayed flights from Atlanta.
To perform the test, we calculate the test statistic and compare it to the critical value from the appropriate distribution.
In this case, we'll use the normal distribution since the sample sizes are reasonably large.
First, let's calculate the proportions of delayed flights for each city:
Proportion of delayed flights from Chicago:
p₁ = 37 / 119 = 0.3109
Proportion of delayed flights from Atlanta:
p₂ = 25 / 127 = 0.1969
Next, we need to calculate the standard error of the difference in proportions:
SE = √(p₁× (1 - p₁) / n₁) + (p₂ × (1 - p₂) / n₂))
where n₁ and n₂ are the sample sizes.
SE = √(0.3109 × (1 - 0.3109) / 119) + (0.1969× (1 - 0.1969) / 127))
= 0.0452
Now, let's calculate the test statistic (z-score):
z = (p₁ - p₂) / SE
z = (0.3109 - 0.1969) / 0.0452
= 2.5298
Looking up the critical value in a standard normal distribution table, we find it to be approximately 1.645.
Since the calculated test statistic (z = 2.5298) is greater than the critical value (1.645), we reject the null hypothesis.
Therefore, there is statistically significant evidence to suggest that the proportion of delayed flights from Chicago is higher than the proportion of delayed flights from Atlanta.
To learn more on Statistics click:
https://brainly.com/question/30218856
#SPJ4
Use the quadratic formula to find the exact solutions of x2 − 9x + 5 = 0.
x equals negative b plus or minus the square root of b squared minus 4 times a times c, all over 2 times a
Answers
Answer:
\(\frac{9\pm\sqrt{61}}{2}\)
Step-by-step explanation:
\(\displaystyle x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}=\frac{-(-9)\pm\sqrt{(-9)^2-4(1)(5)}}{2(1)}=\frac{9\pm\sqrt{81-20}}{2}\\\\=\frac{9\pm\sqrt{61}}{2}\)
A sports club has 140 junior members, 695 adult members, and 210 senior members. What is the probability that the first member selected at random will not be a senior member?
Answers
Answer: The total number of members in the club is 140 + 695 + 210 = 1,045.
The number of non-senior members is 140 + 695 = 835.
The probability that the first member selected at random will not be a senior member is 835 / 1,045 = 0.798 or 79.8%.
So, the answer is 0.798 or 79.8%.
Step-by-step explanation: