Answers
7-3= 4
so x will equal 4 :)
Answer:
x = 4
Step-by-step explanation:
Method 1:
x + 3 = 7
x = 7 - 3
x = 4
Method 2:
x + 3 - 3 = 7 - 3
x = 7 - 3
x = 4
Related Questions
What is the probability that a randomly chosen young adult has at least a high school education? which rule of probability did you use to find the answer?
Answers
The probability that a randomly chosen young adult has at least a high school education can be found using the rule of probability called the "complement rule".
To find the answer, we need to subtract the probability that a randomly chosen young adult does not have at least a high school education from 1. In other words:
Probability of having at least a high school education = 1 - Probability of not having at least a high school education.
By using this rule, we can calculate the probability.
To know more about probability refer here:
https://brainly.com/question/31828911
#SPJ11
Select the correct answer Which is the correct simplified form of the expression (4m-2n^8)^1/2 ———— 9m^-6 n^-8
Answers
Answer:
\(= \frac{2m^2n^8}{3}\)
Step-by-step explanation:
Given expression is
\((\frac{4m^{-2}n^8}{9m^{-6}n^{-8}} )^{\frac{1}{2}\)
The correct simplified form is shown below:-
From the above equation, we will simplify
we will shift \(m^{-6}\) to the numerator and we will use the negative exponent rule, that is
\(= (\frac{4m^{-2}n^8m^6}{9n^{-8}} )^{\frac{1}{2}\)
now we will shift the \(n^{-8}\) to the numerator and we will use the negative exponent rule, that is
\(= (\frac{4m^{-2}n^8m^6n^8}{9} )^{\frac{1}{2}\)
here we will solve the above equation which is shown below
\(= (\frac{4m^4n^{16}}{9}) ^\frac{1}{2}\)
So,
\(= (\frac{(2)^2(m^2)^2(n^8)^2}{(3)^2} ^\frac{1}{2}\)
Which gives result
\(= \frac{2m^2n^8}{3}\)
Question 10 of 10
Which of the following is the surface area of the right cylinder below?
ge
OA. 192g units2
OB. 72 units2
OC. 176 units2
OD. 144g units
SUBMIT

Answers
The surface area of the right cylinder in terms of pi is 76π units².
What is the surface area of the right cylinder?A cylinder is simply a 3-dimensional shape having two parallel circular bases joined by a curved surface.
The surface area of a cylinder is expressed as;
Surface area = ( 2πr² ) + ( 2πrh )
Where r is the radius of the circular base, h is height and π is constant pi.
From the diagram:
Radius r = 8 units
Height h = 3 units
Surface area =?
Plug the given values into the above formula and solve for the surface area:
Surface area = ( 2πr² ) + ( 2πrh )
Surface area = ( 2π × 8² ) + ( 2π × 3 × 8 )
Surface area = ( 2π × 64 ) + ( 2π × 24 )
Surface area = 128π + 48π
Surface area = 176π units²
Therefore, the surface area is 176π units².
Option C) 176π units² is the correct answer.
Learn about volume of cylinder here: brainly.com/question/16788902
#SPJ1
the same 20 contestants on each of 3 days, answered 5 questions in order to when a prize. what is the probablity that they recieved a score of 5
Answers
The probability that each of the 20 contestants receives a score of 5 is 1 divided by 2 raised to the power of 20.
The question is asking for the probability that the same 20 contestants, over the course of 3 days, each answered 5 questions correctly in order to win a prize.
To find the probability, we need to consider the total number of possible outcomes and the favorable outcomes.
First, let's determine the total number of possible outcomes. Since there are 20 contestants and each contestant can answer each question in 2 ways (correct or incorrect), the total number of possible outcomes for each question is 2^20.
Now, let's consider the favorable outcomes. For each contestant to receive a score of 5, they need to answer all 5 questions correctly. There is only one way for each contestant to achieve this. So, the number of favorable outcomes is 1^20.
Therefore, the probability that each of the 20 contestants receives a score of 5 is:
P = Number of favorable outcomes / Number of possible outcomes
P = 1^20 / 2^20
Simplifying this expression, we have:
P = 1 / 2^20
So, the probability that each of the 20 contestants receives a score of 5 is 1 divided by 2 raised to the power of 20.
To learn more about probability
https://brainly.com/question/13604758
#SPJ11
A regular hexagonal prism has a base area of 84.3ft^2 and a Volume of 337.2ft^3. What is the height of the prism?
Answers
Answer:
Height = 4 ft
Step-by-step explanation:
Base are : 84.3 ft square
Volume : 337.2 square cuboid
The auxiliary equation for the given differential equation has complex roots. Find a general solution. 12y" - 12y' + 30y = 0 y(t) =
Answers
Answer:
The given differential equation is:
12y" - 12y' + 30y = 0
To find the general solution, we first need to find the auxiliary equation. We assume a solution of the form:
y(t) = e^(rt)
where r is a constant. Differentiating this equation twice with respect to t, we get:
y'(t) = re^(rt)
y''(t) = r^2 e^(rt)
Substituting these into the differential equation, we get:
12r^2 e^(rt) - 12re^(rt) + 30e^(rt) = 0
Dividing both sides by e^(rt), we get:
12r^2 - 12r + 30 = 0
Simplifying this equation by dividing both sides by 6, we get:
2r^2 - 2r + 5 = 0
This is a quadratic equation with complex roots, which are given by the formula:
r = (2 ± sqrt(-4))/4 = (1 ± i√6)/2
Therefore, the general solution to the differential equation is:
y(t) = c1 e^((1+i√6)/2)t + c2 e^((1-i√6)/2)t
where c1 and c2 are constants determined by the initial conditions or boundary conditions of the problem.
Therefore , the solution of the given problem of equation comes out to be c1*e((1/2)*t)*cos((3/2)t) + c2e((1/2)*t)*sin((3/2)*t) = y(t).
What is an equation?The equation y=mx+b serves as the basis for a linear regression model. B is the slope, and m is the y-intercept. The above line is commonly referred to as the "mathematical problems with two variables," even though y and y are distinct components. Bivariate linear equations only contain two variables. The application areas of linear functions do not have clear-cut solutions.
Here,
For the specified differential equation, the auxiliary equation is:
=> 12r² - 12r + 30 = 0
When we multiply both parts by 6, we get:
=> 2r² - 2r + 5 = 0
Given that the discriminant is negative, the solutions of this quadratic equation are complicated:
=> b² - 4ac = (-2) ² - 4(2)(5) = -36
The following are the roots:
=> r = (2 ± √(-36))/(4) = (1 ± 3i)/2
The differential equation has the following general solution:
=> Y(t) = C1E + C2E (R1T) (r2t)
where c1 and c2 are arbitrary values and r1 and r2 are the auxiliary equation's roots.
When we replace the stems, we obtain:
=> c1*e((1/2)*t)*cos((3/2)t) + c2e((1/2)*t)*sin((3/2)*t) = y(t).
As a result, the differential equation has the following general solution:
=> c1*e((1/2)*t)*cos((3/2)t) + c2e((1/2)*t)*sin((3/2)*t) = y(t).
To know more about linear equation visit:
https://brainly.com/question/11897796
#SPJ1
the spinner below is spun.What is the probability of spinning

Answers
WHO HAS THE ANSWER!! I DONT GET IT. PLEASE COMMENT THE ANSWER ON MY POST
Find an equation of the plane.
The plane through the origin and the points (2, –4, 6) and (5, 1, 3)
Answers
The equation of the plane through the origin and the points (2, –4, 6) and (5, 1, 3) is - 9x + 12y + 11 x = 0.
The general equation of a plane through (0, 0, 0) is a(x - 0) + b(y - 0) + c(z - 0) = 0
Since the plane passes though the origin, the equation of the plane is given by ( x, y, z ) = 0. Simplify it so that you write the equation of the plane in the form a x + b y + c z = 0
ax + by + cx = 0...(1)
It will pass through B(2, -4, 6) and C(5, 1, 3) if
a(2) + b(-4) + c(6) = 0
2a - 4b + 6c = 0
a - 2b + 3c = 0 ...(2)
a(5) + b(1) + c(3) = 0
5a + b + 3c = 0 ... (3)
Solving (2) and (3) by cross-multiplication, we have
\(& \frac{a}{-6-3}=\frac{b}{15-3}=\frac{c}{1+10} \\\)
\(& \Rightarrow \frac{a}{-9}=\frac{b}{12}=\frac{c}{11}=\lambda\) (say) }
\(& \Rightarrow\) a = - 9 \(\lambda\), b = 12 \(\lambda\) and c = 11 \(\lambda\)
Substituting the values of a, b and c in (1), we get
- 9 \(\lambda\) x + 12 \(\lambda\) y + 11 \(\lambda\) x = 0
- 9x + 12y + 11 x = 0
which is the required equation of the plane.
For more questions on equation of the plane
https://brainly.com/question/15683790
#SPJ4
describe in words the set of all points (x;y) in the plane that satisfy the equation (x1) 2 (y 5) 2
Answers
The equation you provided, (x²)(y⁵) = 2, represents a curve in the plane. To describe the set of all points (x, y) that satisfy this equation, we need to analyze the behavior of the equation and examine the properties of the curve it represents.
The equation is a product of two terms: (x²) and (y⁵). This means that for any point (x, y) on the curve, both of these terms must multiply together to equal 2. As a result, the equation does not represent a simple geometric shape like a line or a circle but rather a more complex curve.
Since the term (x²) is squared, it will always be positive or zero, regardless of the value of x. On the other hand, the term (y⁵) is raised to an odd power, which means it can take positive, negative, or zero values depending on the sign of y.
Considering the equation (x²)(y⁵) = 2, there are multiple ways for the product of (x²) and (y⁵) to equal 2. For instance, we could have (x²) = 1 and (y⁵) = 2, or (x²) = 2 and (y⁵) = 1, or even (x²) = 0.5 and (y⁵) = 4, and so on. The possibilities for x and y values are infinite.
Overall, the set of all points (x, y) in the plane that satisfy the equation (x²)(y⁵) = 2 is a complex curve with various branches and regions, where the x-coordinate squared and the y-coordinate to the power of five combine to produce a product of 2. Without further constraints or limits, it is difficult to provide a more specific description of this set of points.
Learn more about equation here
https://brainly.com/question/10238407
#SPJ4
Algebra 2 Problem! Rational Roots
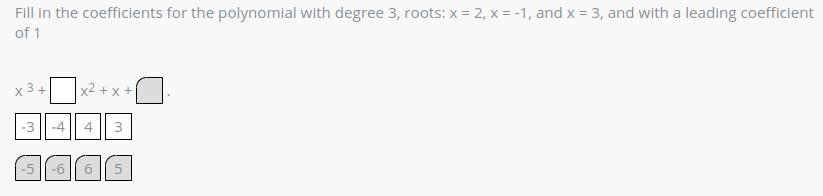
Answers
Answer:
este no hablo inglés
The temperatures (in degrees Fahrenheit) observed during seven days of summer in Los Angeles are:
78 99 68
91
95 75 85
The range of these temperatures is:
The variance of these temperatures, rounded to three decimals, is:
The standard deviation, rounded to three decimals, of these temperatures is:
Answers
The range, variance, and standard deviation of these temperatures is 31, 127.953, and 11.312, respectively.
The range of temperatures is the difference between the highest and lowest temperatures. With the given data, the range can be calculated as follows:
Range = Maximum temperature - Minimum temperature
= 99 - 68
= 31
So, the range of temperatures during the seven days of summer in Los Angeles is 31 degrees Fahrenheit.
The variance is a measure of how spread out the data is. The formula for variance for a sample of n observations is given by:
Variance = (Σ(x - μ)²)/n
Where x is the temperature on the i-th day, and μ is the mean of the temperatures
Upon calculation, the variance is equal to 127.9533.
Rounding the variance to three decimals, the variance is 127.953.
The standard deviation is the square root of the variance and it provides a measure of the spread of the data. The formula for standard deviation is given by:
Standard deviation = √(variance)
So, the standard deviation can be calculated as follows:
Standard deviation = √(127.9533) = 11.3116
Rounding the standard deviation to three decimals, the standard deviation is 11.312 degrees Fahrenheit.
Learn more about standard deviation here: https://brainly.com/question/475676
#SPJ4
An inclined plane that forms a 30° angle with the horizontal is thus released from rest, allowing a thin cylindrical shell to roll down it without slipping. Therefore, we must determine how long it takes to travel five metres. Given his theta, the distance here will therefore be equivalent to five metres (30°).
Answers
The transformation of System A into System B is:
Equation [A2]+ Equation [A 1] → Equation [B 1]"
The correct answer choice is option D
How can we transform System A into System B?
To transform System A into System B as 1 × Equation [A2] + Equation [A1]→ Equation [B1] and 1 × Equation [A2] → Equation [B2].
System A:
-3x + 4y = -23 [A1]
7x - 2y = -5 [A2]
Multiply equation [A2] by 2
14x - 4y = -10
Add the equation to equation [A1]
14x - 4y = -10
-3x + 4y = -23 [A1]
11x = -33 [B1]
Multiply equation [A2] by 1
7x - 2y = -5 ....[B2]
So therefore, it can be deduced from the step-by-step explanation above that System A is ultimately transformed into System B as 1 × Equation [A2] + Equation [A1]→ Equation [B1] and 1 × Equation [A2] → Equation [B2].
The complete image is attached.
Read more equations:
brainly.com/question/13763238
#SPJ1
9.11 algebra 2x2 linear equations pg. 363 (15 points) (no uml required) design a class named linearequation for a 2-by-2 system of linear equations: ax by
Answers
A class named linear equation for a 2-by-2 system of linear equations given below:
Source Code in C++:
#include <iostream>
using namespace std;
class LinearEquation
{
private:
double a,b,c,d,e,f; //private data fields
public:
LinearEquation(double a,double b,double c,double d,double e,double f) //parametrized constructor
{
this->a=a;
this->b=b;
this->c=c;
this->d=d;
this->e=e;
this->f=f;
}
//getter methods
double getA()
{
return a;
}
double getB()
{
return b;
}
double getC()
{
return c;
}
double getD()
{
return d;
}
double getE()
{
return e;
}
//solution functions
double getF()
{
return f;
}
double getX()
{
return (e*d-b*f)/(a*d-b*c);
}
double getY()
{
return (a*f-e*c)/(a*d-b*c);
}
bool isSolvable()
{
if(a*d-b*c==0)
return false;
return true;
}
};
int main()
{
double a,b,c,d,e,f;
cout << "Enter the value of a: "; //input prompt
cin >> a; //input
cout << "Enter the value of b: "; //input prompt
cin >> b; //input
cout << "Enter the value of c: "; //input prompt
cin >> c; //input
cout << "Enter the value of d: "; //input prompt
cin >> d; //input
cout << "Enter the value of e: "; //input prompt
cin >> e; //input
cout << "Enter the value of f: "; //input prompt
cin >> f; //input
LinearEquation ob(a,b,c,d,e,f); //creating new object
if(ob.isSolvable())
cout << "x: " << ob.getX() << " y: " << ob.getY() << endl; //output
else
cout << "The equation has no solution" << endl; //output
return 0;
}
Output:
Learn more about linear equation here;
https://brainly.com/question/33237313
#SPJ4
Complete Question:


Vector a is expressed in magnitude and direction form as a = (V30, 110°). What is the component form a? Enter your answer, rounded to the nearest hundredth, by filling in the boxes.
Answers
The component form of vector a is approximately (-10.26, 25.86).
To find the component form of vector a, we need to use trigonometry.
The magnitude V of the vector a is given by the first component of the magnitude and direction form, which is V = 30.
The angle θ between the vector and the positive x-axis is given by the second component of the magnitude and direction form, which is 110°.
To find the x-component, we use the formula:
x = V cos(θ)
Substituting the values we get:
x = 30 cos(110°) ≈ -10.26
To find the y-component, we use the formula:
y = V sin(θ)
Substituting the values we get:
y = 30 sin(110°) ≈ 25.86.
For similar question on vector.
https://brainly.com/question/30556898
#SPJ11
Select all of the expressions that are equivalent to 5% of 60. 1/20(60), 1/5 times 60, 0.05 times 60, 0.5 times 60, 0.5(60), 5/100 times 60
Answers
The expressions that are equivalent to 5% of 60 are 5/100 * 60, 0.05 * 60 and 1/20 * 60
How to determine the expressions that are equivalent to 5% of 60?The expression is given as:
5% of 60
Express as fraction and decimal
5% of 60 = 5/100 * 60
5% of 60 = 0.05 * 60
This gives
5% of 60 = 1/20 * 60
Hence, the expressions that are equivalent to 5% of 60 are 5/100 * 60, 0.05 * 60 and 1/20 * 60
Read more about expressions at:
https://brainly.com/question/723406
#SPJ4
the transformation shown is a reflection
true or false

Answers
Answer:
False.
Step-by-step explanation:
False. In a reflection, either the x coordinate or the y coordinates of the shape have to be multiplied by -1.
This is a rotation.
solve the system of differential equations dx/dt = 4x 7y dy/dt= x-2y
Answers
The general solution to this system of differential equations is given by: x(t) = C1 * \(e^3^t\) + C2 * (-7t * \(e^t\) ), y(t) = C1 * \(e^3^t\) - C2 * 4t * \(e^t\) , where C1 and C2 are constants.
To solve this system, we follow these steps:
1. Write the given system in matrix form: d/dt [x, y] = [A] * [x, y], where A = [4, 7; 1, -2].
2. Calculate the eigenvalues of matrix A: det(A - λI) = 0. The eigenvalues are λ1 = 3, λ2 = -1.
3. Find the eigenvectors associated with each eigenvalue: (A - λI)v = 0. For λ1 = 3, v1 = [1; 1]. For λ2 = -1, v2 = [-7; 4].
4. Form the general solution using the eigenvectors and eigenvalues: x(t) = C1 * \(e^\lambda^_1t\)* v1 + C2 * \(e^\lambda^_2t\) * v2. In this case, x(t) = C1 * \(e^3^t\) + C2 * (-7t * \(e^t\) ) and y(t) = C1 * \(e^3^t\) - C2 * 4t * \(e^t\) .
To know more about differential equations click on below link:
https://brainly.com/question/31583235#
#SPJ11
Circles. Transition Math HELP ??

Answers
Answer: Choice B) 50 square meters
Work Shown:
A = pi*r^2
A = 3.14*4^2
A = 50.24
A = 50
A 5-card poker hand is said to be a full house if it consists of 3 cards of the same denomination and 2 other cards of the same denomination (of course, different from the first denomination). Thus, a full house is three of a kind plus a pair. What is the probability that one is dealt a full house
Answers
Therefore, the probability of being dealt a full house in a 5-card poker hand is approximately 0.00144 or 0.144%.
To calculate the probability of being dealt a full house in a 5-card poker hand, we need to consider the total number of possible hands and the number of favorable hands (full houses).
Total number of possible hands:
There are 52 cards in a standard deck, and we choose 5 cards for our hand. So, the total number of possible hands is given by the combination formula:
C(52, 5) = 52! / (5! * (52 - 5)!)
= 2,598,960
Number of favorable hands (full houses):
To form a full house, we need to consider the choices for the three cards of one denomination and the two cards of another denomination.
Number of choices for the denomination of three cards: We have 13 denominations (2, 3, 4, ..., 10, J, Q, K, A) to choose from.
Number of ways to choose the three cards of one denomination: We have 4 cards of each denomination in a deck. Therefore, we have C(4, 3) = 4 ways to choose three cards of one denomination.
Number of choices for the denomination of two cards: We have 12 remaining denominations (since we already used one for the three cards).
Number of ways to choose the two cards of another denomination: We have C(4, 2) = 6 ways to choose two cards of another denomination.
To calculate the total number of favorable hands, we multiply these choices:
Number of favorable hands = 13 * C(4, 3) * 12 * C(4, 2) = 13 * 4 * 12 * 6
= 3,744
Now we can calculate the probability by dividing the number of favorable hands by the total number of possible hands:
Probability of getting a full house = Number of favorable hands / Total number of possible hands
= 3,744 / 2,598,960
≈ 0.00144
To know more about probability,
https://brainly.com/question/29580548
#SPJ11
HELPPPPP PLEASEEEEEEEE !!!!!!!!!!!!!!!!!!!!!
Penelope is moving and must rent a truck. There is an initial charge for the rental plus a fee per mile driven. Let C represent the total cost of renting the truck when the truck is driven m miles. A graph of C is shown below. Write an equation for C then state the y-intercept of the graph and determine its interpretation in the context of the problem.
Answers
Answer:
Step-by-step explanation:
I don't see a graph, but I'll answer what I can.
C = total cost of truck rental
. . will be equal to the initial charge, which I'll call IC, and a fee per mile, which I'll call F. m is the miles driven.
C = IC + Fm [Total cost is the initial cost plus mileage charge for m miles].
Rewrite this in standard format of y = mx + b, where m is the slope and b is the y-intercept.
C = Fm + IC
The graph will be a straight line with slope F and y-intercept IC. The x axix is miles driven, and the y axis is Total Cost. If the mileage fee were $0.20/mile, the slope would be 0.20.
The attached graph is the result for IC = $100 and F is $0.20/mile. Miles are on the x axis and total cost on the y.

Divide Whole Numbers - Tutorial - Level U
The first section has 90 sheep sorted into 3 rows. How many sheep are
in each row of the first section?

Answers
Answer:
30 sheep
Step-by-step explanation:
The first section has 90 sheep sorted into 3 rows. How many sheep are
in each row of the first section?
From the above question:
3 rows = 90 sheep
1 row = x
Cross Multiply
3 rows × x = 1 row × 90 sheep
x = 1 row × 90 sheep/3 rows
x = 30 sheep
Therefore, there are 30 sheep in each row of the first section
what’s the area besties?

Answers
Answer:
36
Step-by-step explanation:
2(4.5*3)=13.5
2(3+7.5)=22.5
13.5+22.5=36
The area of a garden can be represented by the expression x2 - 6x - 27. What are the dimensions of the rectangle in terms of x?
Answers
Answer:
Step-by-step explanation:
x² - 6x - 27
x² - 9x + 3x - 27
x(x - 9) + 3(x - 9)
(x - 9) (x + 3) = 0
x = 9
x = -3
The dimensions are 9 and 3
What is this number in standard form? (3×100)+(1×1/10)+(4×1/1,000) Enter your answer in the box. please help fast . im panicking . btw it has to be decimal form
Answers
Answer:
300.104
Step-by-step explanation:
I posted a photo what the difference between expanded and standard form.
Hope this helped

Jill wants to have ride at least 144 miles on her bike. Her riding speed is 9 miles per hour. Which inequality(s) represents how many h hours she needs to ride?
Answers
Hey there!
Let's make an equation
=> 9h = 144
{ Make h the subject of formula}
=> 9h = 144
=> 9h/9 = 144/9
=> h = 144/9
=> h = 16
Is -18/6 > -4? Sorry if it’s a simple answer I got a new calculator and am trying to get use to it so
Answers
Answer:
Yes, because -18/6 is -3, which is a higher value than -4 :)
Define convenience purchases, shopping purchases, and specialty purchases. Describe three specific brand name products in the consumer marketplace today that would correspond to these three types of purchases.
Answers
Convenience purchase: Coca-Cola. Shopping purchase: Apple iPhone. Specialty purchase: Rolex. These brand name products correspond to their respective purchase types based on convenience, shopping involvement, and specialty appeal in the consumer marketplace.
Convenience purchases refer to low-involvement purchases made by consumers for everyday items that are readily available and require minimal effort to obtain. These purchases are typically driven by convenience and habit rather than extensive consideration or brand loyalty.
Shopping purchases involve higher involvement and more deliberate decision-making. Consumers invest time and effort in comparing options, seeking the best value or quality, and may consider multiple brands before making a purchase. These purchases often involve durable goods or products that require more consideration.
Specialty purchases are distinct and unique purchases that cater to specific interests, preferences, or hobbies. These purchases are driven by passion, expertise, and a desire for premium or specialized products. Consumers are often willing to invest more in these purchases due to their unique features, quality, or exclusivity.
Three specific brand name products in the consumer marketplace that correspond to these types of purchases are
Convenience Purchase: Coca-Cola (Soft Drink)
Coca-Cola is a widely recognized brand in the beverage industry. It is readily available in various sizes and formats, making it a convenient choice for consumers seeking a refreshing drink on the go.
With its widespread availability and strong brand presence, consumers often make convenience purchases of Coca-Cola without much thought or consideration.
Shopping Purchase: Apple iPhone (Smartphone)
The Apple iPhone is a popular choice for consumers when it comes to shopping purchases. People invest time researching and comparing features, pricing, and user reviews before making a decision.
The shopping process involves considering various smartphone brands and models to ensure they select a product that meets their specific needs and preferences.
Specialty Purchase: Rolex (Luxury Watches)
Rolex is a well-known brand in the luxury watch industry and represents specialty purchases. These watches are associated with high-quality craftsmanship, precision, and exclusivity.
Consumers who are passionate about luxury watches and seek a premium product often consider Rolex due to its reputation, heritage, and unique features. The decision to purchase a Rolex involves a significant investment and is driven by the desire for a prestigious timepiece.
These examples illustrate how different types of purchases align with specific brand name products in the consumer marketplace, ranging from convenience-driven choices to more involved shopping decisions and specialty purchases driven by passion and exclusivity.
To know more about Convenience purchases:
https://brainly.com/question/30247858
#SPJ4
consider rolling dice and getting a total of 8 which is more likely: rolling a total of 8 when two dice are rolled or rolling a total of 8 when three dice are rolled?
Answers
Rolling a total of 8 when two dice are rolled is more likely than rolling a total of 8 when three dice are rolled.
This is because there are more combinations of two dice that can add up to 8 (four combinations; 1-7, 2-6, 3-5, 4-4) than there are combinations of three dice (three combinations; 1-3-4, 2-2-4, 3-3-2).
Therefore, the probability of rolling a total of 8 with two dice is greater than the probability of rolling a total of 8 with three dice.
Additionally, the odds of rolling a total of 8 with two dice can be calculated using the formula (Number of favourable outcomes/Total number of outcomes) x 100%.
In this case, the formula would be (4/36) x 100%, which equals 11.11%. The odds of rolling a total of 8 with three dice is calculated using the same formula, which would be (3/216) x 100%, which equals 1.39%.
This shows that the odds of rolling a total of 8 with two dice is much greater than the odds of rolling a total of 8 with three dice.
To learn more about combinations visit:
https://brainly.com/question/28065038
#SPJ4
In a class of students, the following data table summarizes how many students play
an instrument or a sport. What is the probability that a student chosen randomly
from the class plays a sport?
Plays a sport
Does not play a sport
Plays an instrument Does not play an instrument
3
8
10
9
Answers
Answer:
3 OR 8 hope this helps!
Step-by-step explanation:
Gilbert purchased a car for 34000. The car depreciates at a rate of 14% per year. The exponential function that represents this situation is y = 34000(0.86)^x.
What is the change factor for this function?

Answers
Answer:
.86
Step-by-step explanation:
Exponential function formula
\(y = a ( 1 + or - r ) ^t\)
where a = initial value
r = rate of change
and t = number of years
given the equation y = 34000(0.86)^x.
r = .86
Hence the change factor is .86
