Find an expression which represents the sum of (4x-2) and (x−8) in simplest terms.

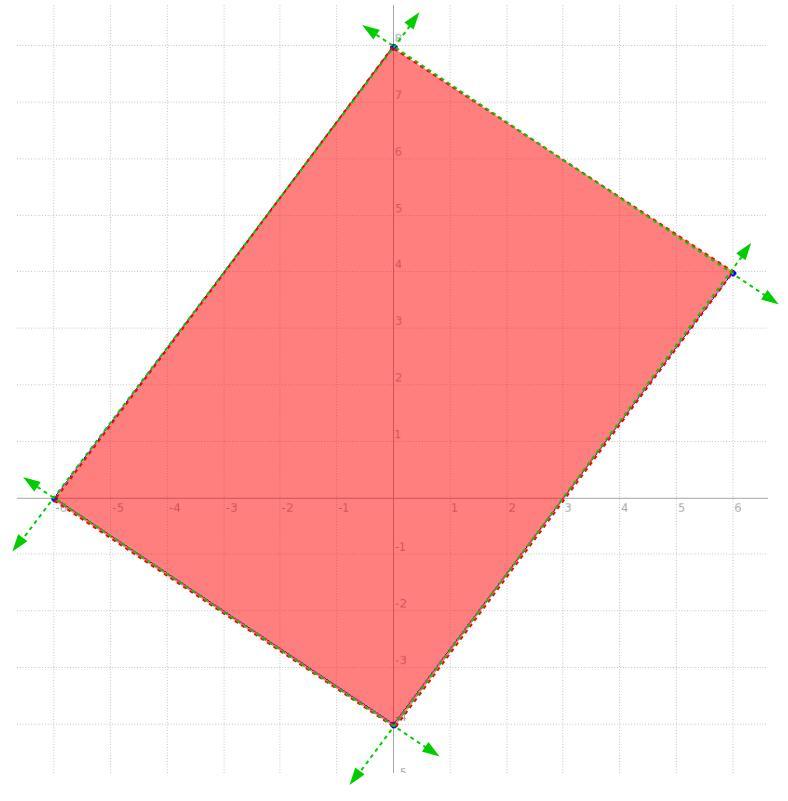
so the idea being, we have a system of equations of two variables and 4 equations, each one rendering a line, for this case these aren't equations per se, they're INEquations, so pretty much the function will be the same for an equation but we'll use > or < instead of =, but fairly the function is basically the same, the behaviour differs a bit.

we have a line passing through (-6,0) and (0,8), side one

we have a line passing through the x-axis and -6, namely (-6,0) and the y-axis and -4, namely (0,-4), side two

we have a line passing through (0,-4) and (6,4), side three

now, side four is simply the line connecting one and three.

the intersection of all four lines looks like the one in the picture below, so what are those lines with their shading producing that quadrilateral?

well, we have two points for all four, and that's all we need to get the equation of a line, once we get the equation, with its shading like that in the picture, we'll make it an inequality.

\((\stackrel{x_1}{-6}~,~\stackrel{y_1}{0})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{8}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{8}-\stackrel{y1}{0}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{(-6)}}} \implies \cfrac{8 -0}{0 +6} \implies \cfrac{ 8 }{ 6 } \implies \cfrac{4}{3}\)

\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{0}=\stackrel{m}{ \cfrac{4}{3}}(x-\stackrel{x_1}{(-6)}) \implies y -0 = \cfrac{4}{3} ( x +6) \\\\\\ y=\cfrac{4}{3}x+8\hspace{5em}\stackrel{\textit{side one} }{\boxed{y < \cfrac{4}{3}x+8}}\)

\(\rule{34em}{0.25pt}\\\\ (\stackrel{x_1}{-6}~,~\stackrel{y_1}{0})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{-4}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{-4}-\stackrel{y1}{0}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{(-6)}}} \implies \cfrac{-4 -0}{0 +6} \implies \cfrac{ -4 }{ 6 } \implies - \cfrac{2}{3}\)

\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{0}=\stackrel{m}{- \cfrac{2}{3}}(x-\stackrel{x_1}{(-6)}) \implies y -0 = - \cfrac{2}{3} ( x +6) \\\\\\ y=-\cfrac{2}{3}x-4\hspace{5em}\stackrel{\textit{side two} }{\boxed{y > -\cfrac{2}{3}x-4}} \\\\[-0.35em] \rule{34em}{0.25pt}\)

\(\stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{4}-\stackrel{y1}{(-4)}}}{\underset{\textit{\large run}} {\underset{x_2}{6}-\underset{x_1}{0}}} \implies \cfrac{4 +4}{6 -0} \implies \cfrac{ 8 }{ 6 } \implies \cfrac{4}{3}\)

\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-4)}=\stackrel{m}{ \cfrac{4}{3}}(x-\stackrel{x_1}{0}) \implies y +4 = \cfrac{4}{3} ( x -0) \\\\\\ y=\cfrac{4}{3}x-4\hspace{5em}\stackrel{ \textit{side three} }{\boxed{y > \cfrac{4}{3}x-4}} \\\\[-0.35em] \rule{34em}{0.25pt}\)

\((\stackrel{x_1}{6}~,~\stackrel{y_1}{4})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{8}) ~\hfill~ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{8}-\stackrel{y1}{4}}}{\underset{\textit{\large run}} {\underset{x_2}{0}-\underset{x_1}{6}}} \implies \cfrac{ 4 }{ -6 } \implies - \cfrac{2}{3}\)

\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{4}=\stackrel{m}{- \cfrac{2}{3}}(x-\stackrel{x_1}{6}) \\\\\\ y=-\cfrac{2}{3}x+8\hspace{5em}\stackrel{ \textit{side four} }{\boxed{y < -\cfrac{2}{3}x+8}}\)

now, we can make that quadrilateral a trapezoid by simply moving one point for "side four", say we change the point (0 , 8) and in essence slide it down over the line to  (-3 , 4).  Notice, all we did was slide it down the line of side one, that means the equation for side one never changed and thus its inequality is the same function.

now, with the new points for side for of (-3,4) and (6,4), let's rewrite its inequality

\((\stackrel{x_1}{-3}~,~\stackrel{y_1}{4})\qquad (\stackrel{x_2}{6}~,~\stackrel{y_2}{4}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{4}-\stackrel{y1}{4}}}{\underset{\textit{\large run}} {\underset{x_2}{6}-\underset{x_1}{(-3)}}} \implies \cfrac{4 -4}{6 +3} \implies \cfrac{ 0 }{ 9 } \implies 0\)

\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{4}=\stackrel{m}{ 0}(x-\stackrel{x_1}{(-3)}) \implies y -4 = 0 ( x +3) \\\\\\ y=4\hspace{5em}\stackrel{ \textit{side four changed} }{\boxed{y < 4}}\)

Answer:

B = 900 Libros

A = 2700 Libros

C = 1800 Libros

Step-by-step explanation:

A = 3B

2B = C

A + B + C = 5400

3B + B + 2B = 5400

6B = 5400

B = 5400 / 6

B = 900 Libros

A = 3B

A = 3(900)

A = 2700 Libros

C = 2B

C = 2(900)

C = 1800 Libros

The linear equation for the cost of lemonades is 1.50*x+6 where x=5 i.e. A   and he spends $54.75 in total.

What is a linear equation ?

A linear equation is an equation in which the highest power of the variable is always 1. It is also known as a one-degree equation. The standard form of a linear equation in one variable is of the form

Ax + B = 0

e.g. x-10=0. Here, x is a variable, A is a coefficient and B is constant.

The standard form of a linear equation in two variables is of the form

Ax + By = C

e.g. 2x-4y=10. Here, x and y are variables, A and B are coefficients and C is a constant.

Now,

Cost of lemonade=$1.5, number of lemonades=5

Cost of hamburger=$8.25, number of hamburgers=5

Tip=$6

Hence,

        Total cost=5*1.5+5*8.25+6

          Total cost =$54.75

Cost of lemonades only = 5*1.5+6

In type of linear equation  1.50*x+6 where x=5

To know more about linear equations visit the link

https://brainly.com/question/29739212?referrer=searchResults

#SPJ1

Answer:

3(−x40000000000000000000+1.1000000033333267e+25)

Step-by-step explanation:

Factor −200000000000+100000000000000000−3x40000000000000000000−2+3.3e+25

−3x40000000000000000000+3.30000000999998e+25

=3(−x40000000000000000000+1.1000000033333267e+25)

Answer:

some big obnoxious number lol

Step-by-step explanation:

The time taken by the person to cover 260 miles will be 3 hours and 15 minutes.

Speed is defined as the ratio of the time distance travelled by the body to the time taken by the body to cover the distance. Speed is the ratio of the distance travelled by time. The unit of speed in miles per hour.

Given that a person to drive 260 miles on a highway if she merges onto a highway at 7 p.m. and drives nonstop with her cruise control set at 80 mph.

The amount of time taken by the person to cover the distance of 260 miles with a speed of 80mph is,

Speed = Distance / Time

Time = Distance / Speed

Time = 260 / 80

Time = 3.25 or 3 hours 15 minutes

Therefore, the time taken by the person to cover 260 miles will be 3 hours and 15 minutes.

To know more about Speed follow

brainly.com/question/6504879

#SPJ1

The value of the underlined digit in the number 27,416,385.( 4 is the underlined number.) is the hundred thousandths place.

The symbols, from 0 to 9 can be described as a digit. For instance, the numbers 2 and 3 are used to represent the number 23.  however amount is represented by a number.

It should be noted that It may be expressed using one, two, three, or even more digits however only single symbol used to represent a number is a digit in the case above we can see that 4 is the hundred thousandths place.

Learn more about digit at:

https://brainly.com/question/26856218

#SPJ1

Answer:

Within 0.5 of ;

is not ;

Step-by-step explanation:

Given the data:

The actual standard deviation, = 1

;

The range rule of thumb to estimate the value if standard deviation is ;

Estimated standard deviation = Range / 4

The range = (maximum - minimum) values

The estimated standard deviation = 4 / 4 = 1

Hence, the estimated standard deviation is with 0.5 of the actual standard deviation, Thus, the estimated standard deviation is not substantially different from the actual standard deviation.

Answer: is 28080

Step-by-step explanation:

Answer:

soln,

we know that;

(n)=(4n+10)then;

(n)=13(4×2+6)

(n)=18(4 × 3 + 6)

The expected value of the car representing the delay of the car at one of the light as per distribution of time is given by option d. 2/3.

For the probability density function of X.

Divide the interval from 0 to 3 minutes into three sub-intervals,

The first minute, during which the car will pass the intersection if the light is green.

The second minute, during which the car will be delayed by one minute if the light is red.

The third minute, during which the car will be delayed by two minutes if the light is red.

The probability of the car arriving during the first sub-interval is 1/3.

If the light is green, the car will pass immediately with no delay.

If the light is red, the car will be delayed by one minute.

So the probability density function of the delay during this sub-interval is,

f(x) ={  1/3, if 0 ≤ x ≤ 1

         0,     otherwise  }

Probability of the car arriving during the second sub-interval is also 1/3.

If the light is red, the car will be delayed by one minute.

If the light is green, the car will be delayed by two minutes.

So the probability density function of the delay during this sub-interval is,

f(x) = { 1/6,      if 1 ≤ x ≤ 2

         1/3,       if 2 ≤ x ≤ 3

         0,          otherwise }

Probability of the car arriving during the third sub-interval is also 1/3.

If the light is red, the car will be delayed by two minutes.

If the light is green, the car will be delayed by three minutes.

But since the car cannot wait for more than three minutes, the delay during this sub-interval is bounded by 2 minutes.

So the probability density function of the delay during this sub-interval is,

f(x) = {  1/6,     if 2 ≤ x ≤ 3

             0,      otherwise  }

Now,

calculate the expected value of X by integrating the product of the delay and the probability density function over the entire range of possible delays

E(X) = \(\int_{0}^{3}\) x f(x) dx

= \(\int_{0}^{1}\)0 dx + \(\int_{1}^{2}\) x (1/6) dx + \(\int_{2}^{3}\) x(1/6) dx

= (1/6)(1/2)  [(2^2 - 1^2) + (3^2 - 2^2)]

= (1/12) [ 3 + 5 ]

= 8/12

= 2/3

Therefore, the expected value of the delay of the car at the light is equal to option d. 2/3.

Learn more about expected value  here

brainly.com/question/15055541

#SPJ4

Answer:

6.0

Step-by-step explanation:

practice many times

Answer:

2 times the square root of 10

Step-by-step explanation:

If you make a right triangle and solve for the hypotenuse (the distance between P1 and P2), you will get 2 times the square root of 10.

Please mark this brainliest.

Answer: \(2\sqrt{10}\)

Step-by-step explanation:

if you draw a triangle starting from P1 and go up to the y value of P2, the change in y is equal to 6.

From that point, go to the right until you hit P2 to get a change in x of 2.

Youre basically missing the hypotenuse of this triangle that you drew. Which is where the distance formula is derived from. 6^2 + 2^2 = s^2

You get √40 = s. It appears that they want you to simplify this square root. What are the two greatest numbers that multiply to equal 40 and atleast one of them has a perfect square root? That's 10 and 4. you can perfectly take the square root of 4, so go ahead and do that. Put that 2 outside of the square root. That gives you \(2\sqrt{10}\)

Answer:

$26.87

Step-by-step explanation:

if the shirt was 35% off, then you paid 65% of the cost

that value can be found by:

39 x .65 = 25.35 (this is the amount paid for the shirt)

sales tax of 6% on 25.35 is:

.06 x 25.35 which equals 1.52

25.35 + 1.52 = 26.87

Answer:

x=1/40

Step-by-step explanation:

1/4 :100= 25 so x: 1000 is just figureing out what amout 25 is of 1000

The value of the probability is P(Large or Blue) = 7/10

The given parameters are represented on the table

Using the table parameters, we have

P(Large or Blue) = [(Large) + (Blue) - (Large and Blue)]/Total

This gives

P(Large or Blue) = ((17 + 8) + (17 +3) - 17)/(17 + 3 + 8 + 12)

This gives

P(Large or Blue) = 28/40

Simplify

P(Large or Blue) = 7/10

Hence, the value of the probability is P(Large or Blue) = 7/10

Read more about probability at:

https://brainly.com/question/24756209

#SPJ1

Answer:

inches

Step-by-step explanation:

well depends on how big your foot is

Answer:

  5.03

Step-by-step explanation:

Answer:

5.03 = AC

Step-by-step explanation:

Since this is a right triangle, we can use trig functions

tan theta = opp/ adj

tan 40 = AC /6

6 tan 40 = AC

5.034597787 = AC

To the nearest hundredth

5.03 = AC

The solution of Equation are (5/2, 4/3).

Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.

It demonstrates the equality of the relationship between the expressions printed on the left and right sides. LHS = RHS is a common mathematical formula.

Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.

Given:

3x+5y=14..........(1)

6x - 4y=9..............(2)

Solving equation (1) and (2) we get

3x + 5y = 14

Subtract 3x from both sides.

5y = 14 - 3x

Divide by 5 on both sides.

y = -3/5x + 14/5

and, 6x - 4y = 9

Subtract 6x from both sides.

-4y = 9 - 6x

Divide by -4 on both sides.

y = 3/2x - 9/4

From the graph we get

x = 2.405

y= 1.375

Learn more about Equation here:

https://brainly.com/question/29657983

#SPJ1

Answer:

There would be a 56% increase

Step-by-step explanation:

We need to find the amount of change before we can find the percent of change. We'll take the greater value, 78, and subtract the lesser value, 50. 78 - 50 = 28. We then take this amount of change and put it over the original amount, Percent of change = Amount of change/ original amount or for this problem, 28/50. We then use that as a division equation for 28 divided by 50. 28 divided by 50 = 0.56. Finally we move the decimal to the right two times and we can then find the percentage increase.

Answer:

<E, <F, <G

Step-by-step explanation:

The equation of the line that passes through point (-3,-7) and point (-3,10) is x = -3.

The formula for equation of line is expressed as;

y = mx + b

Where m is slope and b is y-intercept.

Given the points through which the line passes: (-3,-7) and (-3,10).

The two given points (-3, -7) and (-3, 10) have the same x-coordinate -3

Hence, the two lines  lie on a vertical line.

since the slope of the vertical line is undefined.

The equation of the line passing through these two points is simply the equation of the vertical line:

x = -3

Learn more about equation of line here: brainly.com/question/2564656

#SPJ1

The value that would have the most dots on a line plot is given as follows:

4.25.

The dot plot gives a dot to each measure for each time that it appears, hence it says the same thing as a table, in a different format.

A line plot is built from the dot plot, in which:

Hence the value 4.25 is the value in this problem that would have the most dots in a line plot, as it is the value that appears the most times in the data-set (only value to appear three times).

More can be learned about dot plot at brainly.com/question/29660457

#SPJ1

The Amy has 42 books, Betty has 36 books, and Carol has 18 books.

Let's set up equations to represent the given information:

Let A represent the number of books Amy has.

Let B represent the number of books Betty has.

Let C represent the number of books Carol has.

Let's say Amy has x books.

Betty has 6 books less than Amy, so Betty has (x - 6) books.

Carol has half as many books as Betty, so Carol has (x - 6)/2 books.

According to the problem, the total number of books they have is 96.

So, we can write the equation:

x + (x - 6) + (x - 6)/2 = 96

To solve the equation, we can simplify it by multiplying through by 2 to remove the fraction:

2x + 2(x - 6) + (x - 6) = 192

2x + 2x - 12 + x - 6 = 192

5x - 18 = 192

5x = 210

x = 42

Amy has 42 books.

Betty has (42 - 6) = 36 books.

Carol has (36)/2 = 18 books.

For more such questions on Amy:

https://brainly.com/question/25319846

#SPJ8

Given:

There are given that the initial amount, time period, and rate are:

Explanation:

To find the present value, we need to use the present value formula:

So,

From the formula of present value:

Then,

Put all the given values into the above formula:

So,

Then,

Final answer:

Hence, the amount is $137023.84

Answer:

None of the above.

No assumptions can be made because we do not know if the function is continuous or differentiable on those intervals.

Answer:

Step-by-step explanation:

18 * 10 - 8 * 4    (remember pemdas)

180 - 32 =

148 cm²

Answer:

37 shots

Step-by-step explanation:

48% = 48/100

Set the ratios equal to each other so that we can find "x" the number of shots she made.

48/100 = x/78

78*48 = 3744

3744/100 = 37.44

She made 37 shots

The remaining Kit volume in the syringe is sufficient to correct the dose to 20 mCi.

To solve this problem, we can use the concept of radioactive decay and the decay factor. Here's how we can calculate the required volume to correct the dose:

Determine the initial activity of the kit:

Initial activity = 180 mCi

Calculate the decayed activity at 9:30 (after 1.5 hours):

Decay factor = 0.841

Decay activity = Initial activity * Decay factor

Calculate the remaining activity after withdrawing 20 mCi at 8 am:

Remaining activity = Initial activity - 20 mCi

Calculate the remaining activity at 9:30:

Remaining activity at 9:30 = Remaining activity * Decay factor

Calculate the desired activity at 9:30 (20 mCi):

Desired activity at 9:30 = 20 mCi

Calculate the volume needed to achieve the desired activity:

Volume needed = Desired activity at 9:30 / Remaining activity at 9:30 * Volume at 9:30

Calculate the remaining volume at 9:30:

Remaining volume = Volume at 8 am - Volume withdrawn - Volume accidentally discharged

Calculate the volume that needs to be added:

Volume to be added = Volume needed - Remaining volume

Let's perform the calculations step by step:

Determine the initial activity of the kit:

Initial activity = 180 mCi

Calculate the decayed activity at 9:30 (after 1.5 hours):

Decay factor = 0.841

Decay activity = 180 mCi * 0.841 = 151.38 mCi

Calculate the remaining activity after withdrawing 20 mCi at 8 am:

Remaining activity = 180 mCi - 20 mCi = 160 mCi

Calculate the remaining activity at 9:30:

Remaining activity at 9:30 = 160 mCi * 0.841 = 134.56 mCi

Calculate the desired activity at 9:30 (20 mCi):

Desired activity at 9:30 = 20 mCi

Calculate the volume needed to achieve the desired activity:

Volume needed = (Desired activity at 9:30 / Remaining activity at 9:30) * Volume at 9:30

Volume at 9:30 = Remaining volume = 30 ml - (30 ml / 2) = 15 ml

Volume needed = (20 mCi / 134.56 mCi) * 15 ml = 2.236 ml

Calculate the remaining volume at 9:30:

Remaining volume = 30 ml - (30 ml / 2) = 15 ml

Calculate the volume that needs to be added:

Volume to be added = Volume needed - Remaining volume = 2.236 ml - 15 ml = -12.764 ml

Since the calculated volume to be added is negative, it means that no additional volume is required. The remaining Kit volume in the syringe is sufficient to correct the dose to 20 mCi.

For such more questions on Kit Volume Correction

https://brainly.com/question/22971212

#SPJ8

The volume of the composite figure in this problem is given as follows:

76 ft³.

The volume of a rectangular prism, with dimensions defined as length, width and height, is given by the multiplication of these three defined dimensions, according to the equation presented as follows:

Volume = length x width x height.

The figure in this problem is composed by two prisms, with dimensions given as follows:

Hence the volume is given as follows:

2 x 6 x 3 + 2 x 4 x 5 = 76 ft³.

A similar problem about the volume of rectangular prisms is presented at brainly.com/question/22070273

#SPJ1