Find the slope using the following two points:
(2,-7) and (-1,6)
Answers
Answer:
13/-3
Step-by-step explanation:
Y2-Y1/X2-X1
Related Questions
The table of paired values represents a proportional relationship.
x 1 3 6 7
y 4 y 24 28
What is the missing y-value in the table?
Responses
8
8
12
12
16
16
I don't know.
I don't know.

Answers
Answer:
12
Step-by-step explanation:
because you can see that in the first column, the y value is 4 times the x value
and in the third column, the y value is still 4 times greater than the x value
meaning that you need to find a number that is 4 times the value of 3 (because that is the x value)
3 times 4 is 12
Steve is 6 years older then Kim . Their age is total is 22
How old is Steve
Answers
Answer:
16
Step-by-step explanation:
22-6=16
The random variable x is the number of occurrences of an event over an interval of ten minutes. It can be assumed that the probability of an occurrence is the same in any two time periods of an equal length. It is known that the mean number of occurrences in ten minutes is 5.
Question: The probability that there are 8 occurrences in ten minutes is
A) 0.0652
B) 0.9319
C) 0.0771
D) 0.1126
Answers
Option C. which corresponds to the probability of approximately 0.0771 that there will be 8 occurrences within a period of ten minutes.
This problem follows a Poisson distribution, where the mean and variance of the distribution are equal to λ. Here, λ = 5, and we need to find the probability of having 8 occurrences in 10 minutes. The probability mass function of Poisson distribution is:
P(X = k) = (e⁽⁻λ⁾ * λᵏ) / k!
Substituting the given values, we get:
P(X = 8) = (e⁽⁻⁵⁾ * 5⁸) / 8!
P(X = 8) ≈ 0.0771
Therefore, the probability that there are 8 occurrences in ten minutes is approximately 0.0771, which corresponds to option C.
This problem follows a Poisson distribution, where the mean and variance of the distribution are equal to λ. Here, λ = 5, and we need to find the probability of having 8 occurrences in 10 minutes. The probability mass function of Poisson distribution is:
P(X = k) = (e⁽⁻λ⁾ * λᵏ) / k!
Substituting the given values, we get:
P(X = 8) = (e⁽⁻⁵⁾ * 5⁸) / 8!
P(X = 8) ≈ 0.0771
Therefore, the probability that there are 8 occurrences in ten minutes is approximately 0.0771, which corresponds to option C.
Learn more about probability here: brainly.com/question/30034780
#SPJ4
Q2: Use Euler's method to approximate y' = y - x for the initial condition y(0) = 1.5,0 ≤x≤ 1.5,h=0.5 with accuracy e=0.0001
Answers
The value of given differential equation \(y' = y - x\) with the initial condition \(y(0) = 1.5\), on the interval \(0 \leq x \leq 1.5\), is \(y(1.5) = y_4 = 5.4296875\).
The differential equation we are given is \(y' = y - x\), with the initial condition \(y(0) = 1.5\). We are asked to approximate the solution on the interval \(0 \leq x \leq 1.5\) with a step size of \(h = 0.5\), and we want to achieve an accuracy of \(e = 0.0001\).
We start by calculating the first two values, \(y_0\) and \(y_1\), using the formula:
\(y_1 = y_0 + h \cdot f(x_0, y_0)\)
Here, \(h\) represents the step size, \(f(x, y)\) represents the derivative \(y'\) in terms of \(x\) and \(y\), and \((x_0, y_0)\) is the initial condition.
Using the given values, we can calculate \(y_1\) as:
\(y_1 = 1.5 + 0.5 \cdot (1.5 - 0) = 2.25\)
Next, we calculate \(y_2\) using the same formula:
\(y_2 = y_1 + h \cdot f(x_1, y_1)\)
Substituting the values \(x_1 = 0.5\) and \(y_1 = 2.25\), we get:
\(y_2 = 2.25 + 0.5 \cdot (2.25 - 0.5) = 3.375\)
Similarly, we can calculate \(y_3\) and \(y_4\) as:
\(y_3 = 3.375 + 0.5 \cdot (3.375 - 1) = 4.3125\)
\(y_4 = 4.3125 + 0.5 \cdot (4.3125 - 1.5) = 5.4296875\)
So, the value of \(y\) at \(x = 1.5\) is \(y(1.5) = y_4 = 5.4296875\).
Using Euler's method with a step size of \(h = 0.5\) and an accuracy of \(e = 0.0001\), the solution to the given differential equation \(y' = y - x\) with the initial condition \(y(0) = 1.5\), on the interval \(0 \leq x \leq 1.5\), is \(y(1.5) = y_4 = 5.4296875\).
To know more about Euler's method, click here
https://brainly.com/question/30699690
#SPJ11
Find all 3 solutions: 3 − 42 − 4 + 5 = 0
Answers
Answer:
Step-by-step explanation:
If you mean 3x^3 - 42x^2 - 4x + 5 = 0 you can graph it manually or with technology
The roots are 14.09, 0.30 and -0.39 to nearest hundredth.
What must be added to 70 so it will divide exactly into five groups of 16
Answers
Answer:
10
Step-by-step explanation:
\(x+70=16(5)\\\\x+70=80\\\\x=10\)
Therefore, the number is 10
Please please please please please please please SOMONE help please

Answers
Answer:
all real numbers greater than or equal to 2
Step-by-step explanation:
the range of a function is the values that y can have.
the minimum value of y is at y = 2
the solid blue circle indicates that y can equal 2.
above y = 2 the values of y keep increasing
range is y ≥ 2 , y ∈ R
The graph shows total cost of a whitewater rafting trip and the corresponding number of passengers on the trip. Find ƒ(8), and explain what it represents.

Answers
Answer:f(n)=259
Step-by-step explanation:
F(n)=75+25(n-1)
F(n)= 75+25(7)
F(n)=75+175
F(n)=250
Find the circumference and area of Circle A and Circle X if each unit on the graph measures 1 centimeter. Round answers to the Nearest tenth, if necessary.
~NUMBER'S 3 AND 4~


Answers
The area and circumference of the circle will be 28.26 square units and 18.84 units, respectively.
What is the circumference and area of a circle?Let r be the radius of the circle. Then the area of the circle will be
A = πr² square units
The circumference of the circle will be
C = 2πr units
From the diagram, the radius of the circle is 3 units. Then the area of the circle will be
A = πr²
A = 3.14 x 3²
A = 3.14 x 9
A = 28.26 square units
Then the circumference of the circle will be
C = 2πr
C = 2 x 3.14 x 3
C = 18.84 units
The area and circumference of the circle will be 28.26 square units and 18.84 units, respectively.
More about the circumference and area of a circle link is given below.
https://brainly.com/question/16125353
#SPJ1
Solve using the quadratic formula. Show all work. Write each solution in simplest form. No decimals.
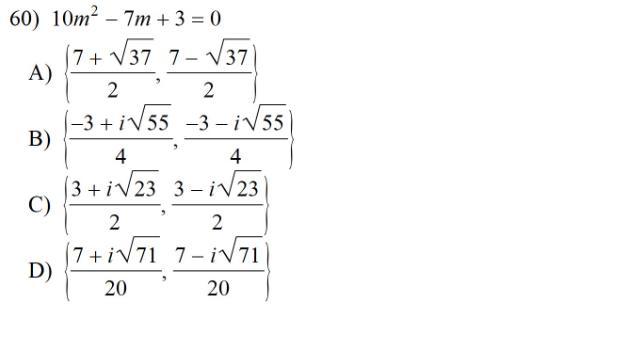
Answers
Given:
The quadratic equation is:
\(10m^2-7m+3=0\)
To find:
The solutions for the given equation by using the quadratic formula.
Solution:
If a quadratic equation is \(ax^2+bx+c=0\), then the quadratic formula is:
\(x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}\)
We have,
\(10m^2-7m+3=0\)
Here, \(a=10,b=-7,c=3\). Using the quadratic formula, we get
\(m=\dfrac{-(-7)\pm \sqrt{(-7)^2-4(10)(3)}}{2(10)}\)
\(m=\dfrac{7\pm \sqrt{49-120}}{20}\)
\(m=\dfrac{7\pm \sqrt{-71}}{20}\)
\(m=\dfrac{7\pm i\sqrt{71}}{20}\) \([\because \sqrt{-a}=i\sqrt{a},a>0]\)
Therefore, the solution set of the given equation is \(\left\{\dfrac{7- i\sqrt{71}}{20},\dfrac{7+ i\sqrt{71}}{20}\right\}\). Hence, the correct option is D.
5.975 x 1024 plsss solve it
Answers
Question 15
2 pts
The playing time X of jazz CDs has the normal distribution with mean 52 and standard deviation 7;
N(52,7).
According to the 68-95-99.7 rule, what percentage of jazz CDs play exactly 50 minutes?
Answers
A paper company needs to ship paper to a large printing business. The paper will be
shipped in small boxes and large boxes. Each small box of paper weighs 50 pounds
and each large box of paper weighs 80 pounds. There were 4 more large boxes
shipped than small boxes and the total weight of all boxes was 1750 pounds. Write a
system of equations that could be used to determine the number of small boxes
shipped and the number of large boxes shipped. Define the variables that you use to
write the system.
Answers
The system of equations that could be used to determine the number of small boxes shipped and the number of large boxes shipped are:
50x+80y=1750
y = x+4 ,
where x represent the number of small boxes of paper and y represent the number of large boxes of paper.
We have:
Weight of small box of paper = 50 pounds
Weight of large box of paper = 80 pounds
Total weight of boxes = 1750 pounds
Let us consider that the number of small boxes of papers be x.
The number of large boxes of papers be y.
Then, according to question
50x+80y=1750
y = x+4
Therefore, the equations 50x+80y=1750 and y = x+4 can be used to determine the number of small boxes and large boxes of paper shipped.
where, x represent the number of small boxes of paper and y represent the number of large boxes of paper.
Statement 1: If √12 - √8 = a, then √12 + √8 is equal to 4/a.
Statement 2: a + √b is called the rationalizing factor of c + √d if their product is 1.
• Statement 1 is true; Statement 2 is true; Statement 2 is the correct explanation of Statement 1.
• Statement 1 is true; Statement 2 is true; 2 is not the correct explanation of Statement 1.
• Statement 1 is true; Statement 2 is false.
• Statement 1 is false; Statement 2 is true.
It is an assertion-reasoning question. Please help me to solve this. Need step-by-step explanation as well. Thank you.
Answers
Answer:
Statement 1 is true; Statement 2 is false.
Step-by-step explanation:
Statement 1:
√12 - √8 = a
Let's use the given value of √12 + √8 ,that is, 4/ a.
If we multiply both the expressions such that their Left Hand Sides get multiplies together and Right Hand Sides together:
=> (√12- √8)(√12 + √8) = a × 4/a
On the LHS,
identity used:
(a-b)(a+b) = a²-b²
On the RHS:
a gets canceled due to its presence in both the numerator as well as the denominator.
=> 12 - 8 = 4
=> 4 = 4
That's it!
We got LHS = RHS, that approves the existence of the given statement.
___________________
Statement 2:
"a + √b is called the rationalizing factor of c + √d if their product is 1"
That's not entirely right!
The correct statement would be:
" a + √b is called the rationalizing factor of c + √d if their product is a rational number ."
Since, rationalizing has got nothing to do with 1, (1 is just another rational number), even if we get 2 by their multiplication, it will be called rationalizing as long as we're getting a rational number.
___________________
Answer:
Hence, I'd say:
Statement 1 is correct but Statement 2 isn't.
That's the third option.
Part A:
A circle is inscribed in a square. Each side of the square is 10 centimeters long.
What is the area of the circle?
Part B:
Find area of the shaded region that is outside the circle but inside the square

Answers
Answer:i think it is 5
Step-by-step explanation:
What is shifted ramp signal?
Answers
A shifted ramp signal is a type of analog signal that starts from a specific value and gradually increases in a linear manner until it reaches another value, at which point it remains constant.
The "shifted" part refers to the starting value, which is not necessarily zero but can be any arbitrary value. This type of signal is commonly used in electronics and signal processing applications, such as in voltage-controlled oscillators and analog-to-digital converters. In essence, a shifted ramp signal is a linearly increasing signal that has been shifted up or down to start from a non-zero value.
You can learn more about analog signal at
https://brainly.com/question/27778793
#SPJ11
quality control for many products involves breaking, destroying, or wearing out a number of the products in order to see exactly what it takes to make the product stop working. suppose that, for one product, 98% of all the units made at a particular factory can hold at least 400 lbs. of weight before breaking. to check the product, quality control selects a random sample of 300 units made at the factory and determines whether or not the product can hold at least 400 lbs. of weight before breaking. what is the probability that the randomly selected sample will have less than 97.5% of the units that can hold at least 400 lbs. of weight before breaking?
Answers
The probability that the randomly selected sample will have less than 97.5% of the units that can hold at least 400 lbs of weight before breaking is 2.4249.
What is the binomial distribution?
In probability theory and statistics, the discrete probability distribution of the number of successes in a series of n separate experiments, each asking a yes-or-no question and each with its own Boolean-valued outcome: success or failure, is known as the binomial distribution with parameters n and p.
Here, we have
Given: For one product, 98% of all the units made at a particular factory can hold at least 400 lbs. of weight before breaking to check the product, quality control selects a random sample of 300 units made at the factory and determines whether or not the product can hold at least 400 lbs.
p = 0.98
q = 1 - p = 1 - 0.98 = 0.02
n = 300
Using the binomial distribution,
Standard deviation = σ = √npq = √300 × 0.98 × 0.02 = 2.4249
Standard deviation = σ = 2.4249
Hence, the probability that the randomly selected sample will have less than 97.5% of the units that can hold at least 400 lbs of weight before breaking is 2.4249.
To learn more about the binomial distribution from the given link
https://brainly.com/question/9325204
#SPJ4
PLEASE HELP!!! I WILL RATE YOU BRAINLIEST
The first laptop ever was sold was the Osborne 1. It came onto the market in 1981, and it had a mass of 11 kg. Suppose that since 1981 the mass of laptops has decreased at an average rate of 4.7% per year. What was the approximate weight of a laptop in 2019?
a. 6.43 kg
b. 8.10 kg
c. 4.62 kg
d. 1.76 kg
Answers
Answer: (d)- 1.76 kg
Step-by-step explanation:
Given
The first laptop mass was 11 kg
The rate of mass decreases by 4.7% per year
In 1982, it was
\(\Rightarrow 11-11\times 4.7\%=11-11\times 0.047\\\Rightarrow 11(1-0.047)\ kg\)
In 1983, it was
\(\Rightarrow 11(1-0.047)-11(1-0.047)\times 0.047=11(1-0.047)^2\)
In 2019 i.e. after 38 years, it is
\(\Rightarrow 11(1-0.047)^38=11\times 0.953^{38}=1.76\ kg\)
Jalen and his 2 brothers each ate 3/4 of a cupcake. How many cupcakes did they eat altogether?
2 cupcakes
1 1/4 cupcakes
2 1/4 cupcakes
2 3/4 cupcakes
Answers
The answer is 2 1/4 cupcakes
Answer:
2 1/4 cupcakes
Step-by-step explanation:
Step 1: State what is know
There are 3 people Jake, Brother 1, and Brother 2. They all ate 3/4 of a cup cake each
Step 2: Solve
Multiple 3 by 3/4
3 x 3/4 = \(C_{Total}\)
2.25 = \(C_{Total}\\\)
0.25=1/4
2 1/4 cupcakes
Step 3: Therefore Statement
Therefore the 3 brothers ate 2 1/4 cupcakes
What is 60 000 in standard form
Answers
Answer:
60.000 x 10 to the power of 3
Step-by-step explanation:
Find the measure of each missing angle explain work

Answers
angle 2: 79 degrees
angle 3: 38 degrees
explanation:
angle 1: 180 - 90 - 38 = 52
angle 2: 180 - 63 - 38 = 79
angle 3: 90 - 52
two points are marked at random on a unit segment. what is the probability that the three obtained segments can be arranged into a triangle?
Answers
The probability that the three segments can be arranged to form a triangle is 1 - 1/6 = 5/6. Answer: 5/6
Let's consider a unit segment that is 1 unit in length. Assume two points A and B are chosen arbitrarily on the segment. Now, we need to determine the probability that the three segments formed by these two points can be arranged to form a triangle. Let these segments be AB, AC, and BC,
where C is any point that lies between A and B.There are several techniques for solving this problem. We'll use the geometric probability approach.
First, we'll draw a diagram of the segment AB and then a point C between A and B. Let the lengths of segments AB, AC, and BC be represented by x, y, and z, respectively, as shown in the figure below. \(\overline{AB}\) is a unit segment and C lies between A and B.
The lengths of \(\overline{AC}\) and \(\overline{BC}\) are x and y units respectively.Let's use the Triangle Inequality theorem to see if these segments can form a triangle.
According to the theorem, the sum of the lengths of any two sides of a triangle must be greater than the length of the third side, or a + b > c, where a, b, and c are the lengths of the sides.
Using this theorem, we can write the following inequalities:x + y > zx + z > yz + y > xAdding these three inequalities together, we get:2x + 2y + 2z > x + y + z, orx + y + z > 1.
Hence, the probability that the three segments can be arranged to form a triangle is 1 - P(x + y + z ≤ 1). Let's compute P(x + y + z ≤ 1) by determining the area of the region where x + y + z ≤ 1. This area is a tetrahedron with a base of area 1/2 and a height of 1/3, giving a volume of 1/6.
To learn more about : probability
https://brainly.com/question/251701
#SPJ8
CAN SOMEONE PLS HELP MEEE(12 questions)

Answers
n = -16 - √336÷2=-8-2√21= 17•165
n=-16+√336
_______
2. = -8+2√21 = 1•165
A candy box is made from a piece of cardboard that measures by inches. Squares of equal size will be cut out of each corner. The sides will then be folded up to form a rectangular box. What size square should be cut from each corner to obtain maximum volume?.
Answers
The maximum volume square candy box to be cut out is 2.88 inches.
What is termed as the maximum volume?The highest values of a dimensions when taking account for measurement error provide the greatest volume of a shape with measured dimensions.If the size of the squares to also be cut out is x, then
the length of the rectangular candy box to also be formed will become 25 - 2x, the width 14 - 2x, and the height x after the squares have been cut out from each corner.A rectangular box's volume is provided by length x width x height.
V = (25 - 2x)(14 - 2x)x = x(350 - 78x + 4x²)
V = 350x - 78x² + 4x³
For the maximum volume of the candy box.
dV/ dt = 0
Differentiate the volume with respect to time.
dV/ dt = 350 - 156x + 12x².
Then,
350 - 156x + 12x² = 0
Solve the above quadratic equation by the quadratic formula and find the roots as-
x = 10.12 and 2.88
However, the size of a square cut out cannot be 10.12 because 10.12 inches cannot be cut from both sides of a 14-inch width.
As a result, the maximum volume square to be cut out is 2.88 inches.
To know more about the maximum volume, here
https://brainly.com/question/17219343
#SPJ4
A company or did copy paper for the office the cost is $52 per box of paper they also had to pay $48 to have it shipped
Answers
Simplify.
N4 x N7 over n5
Answers
Answer:
\(n^6\).
Step-by-step explanation:
\(n^4 * \frac{n^7}{n^5}\)
= \(n^4 * n^{7 - 5}\)
= \(n^4 * n^2\)
= \(n^{4 + 2}\)
= \(n^6\).
Hope this helps!
give the geometrical representation of y=3 as an equation in
a) one variable
b) in two variables.
Answers
The geometrical representation of y=3 as an equation in
a) one variable is y = 3
b) in two variables is 0x + y = 3.
How to illustrate the information?Based on the information illustrated, the geometrical representation of y=3 as an equation in one variable is y = 3.
Also, the geometrical representation of y=3 as an equation in two variables is:
y = 3.
0x + y = 3
0x + y - 3 = 0
Therefore, y = 3.
Learn more about equations on:
brainly.com/question/18831322
#SPJ1
What is the value of X in the equation below?

Answers
Answer:
1/3 is the correct answer...
Hope it helps!!!!
an exam grade data for a statistics class has been observed to have a mean of 36.12 and standard deviation of 3.53. what is the probability that the exam scores are at least 37?
Answers
The probability that the exam scores are at least 37 is 0.4013 or 40.13%
The probability that the exam scores are at least 37 can be calculated using the normal distribution function. To calculate the probability, we first need to standardize the variable using the formula z = (x - μ) / σ, where x is the value of interest (in this case, x = 37), μ is the mean, and σ is the standard deviation.
z = (37 - 36.12) / 3.53 = 0.25
Using a standard normal distribution table or a calculator, we can find the probability that a standard normal random variable is greater than or equal to 0.25, which is approximately 0.4013.
Therefore, the probability that the exam scores are at least 37 is 0.4013 or 40.13%
To learn more about probability here;
brainly.com/question/30034780#
#SPJ11
Ciara measured the length, x, of each of the insects she found underneath a rock. She recorded the lengths in the table below. Calculate an estimate of the mean length of the insects she found. Give your answer in millimetres (mm). Length (mm) 0≤x≤10 10≤x≤20 20≤x≤30 Frequency 5 6 9
Answers
The estimate of the mean length of the insects Ciara found is 17 millimeters (mm).
To calculate an estimate of the mean length of the insects Ciara found, we need to find the weighted average of the lengths using the given frequencies.
Let's denote the lower limits of the length intervals as L1 = 0, L2 = 10, and L3 = 20.
Similarly, denote the upper limits as U1 = 10, U2 = 20, and U3 = 30.
Next, we calculate the midpoints of each interval by taking the average of the lower and upper limits.
The midpoints are M1 = (L1 + U1) / 2 = 5, M2 = (L2 + U2) / 2 = 15, and M3 = (L3 + U3) / 2 = 25.
Now, we can calculate the sum of the products of the frequencies and the corresponding midpoints.
This gives us (5 \(\times\) 5) + (6 \(\times\) 15) + (9 \(\times\) 25) = 25 + 90 + 225 = 340.
Next, we calculate the sum of the frequencies, which is 5 + 6 + 9 = 20.
Finally, we divide the sum of the products by the sum of the frequencies to find the weighted average, which is 340 / 20 = 17.
Therefore, the estimate of the mean length of the insects Ciara found is 17 millimeters (mm).
Thus, the mean length of the insects Ciara found is approximately 17 millimeters (mm).
For similar question on mean length.
https://brainly.com/question/16971437
#SPJ8