Answers
Answer:
358.5 sq-in
Step-by-step explanation:
This is the answer.





Related Questions
To solve the system of linear equations 3 x minus 2 y = 4 and 9 x minus 6 y = 12 by using the linear combination method, Henry decided that he should first multiply the first equation by –3 and then add the two equations together to eliminate the x-terms. When he did so, he also eliminated the y-terms and got the equation 0 = 0, so he thought that the system of equations must have an infinite number of solutions. To check his answer, he graphed the equations 3 x minus 2 y = 4 and 9 x minus 6 y = 12 with his graphing calculator, but he could only see one line. Why is this?
Answers
Henry could only see one line since both lines had the same slope, which means that the graphs of both equations will be identical and hence overlap.
Identify the linear equation?Linear equations in a system 3x + 2y = 4, and 9x + 6y = 12
We must demonstrate why Henry could only make out one line when he plotted the equations 3x-2y=4 and 9x-6y=12 on a graph.
Take the provided linear equation system into consideration.
3x - 2y = 4 ................(1)
9x - 6y = 12 ..................(2)
Due to the fact that equation (2) is a multiple of equation (1), 3 (3x - 2y = 4) = 9x - 6y = 12
The slopes of the provided equations are also same.
Difference with regard to x for equation (1) yields,
additional to equation (2),
With regard to x, we can differentiate to get,
The graphs of both equations will overlap since both lines have the same slope and hence have the same appearance on the graph.
To learn more about linear equations refer to:
https://brainly.com/question/2030026
#SPJ1
Please help me I really need this

Answers
Answer:
yes
Step-by-step explanation:
In a recent survey, 45% indicated chocolate was their favorite flavor of ice cream. Suppose we select a sample of fourteen people and ask them to name their favorite flavor of ice cream. (a) How many of those in the sample would you expect to name chocolate? (Round your answer to 2 decimal places.) Expected number of people (b) What is the probability exactly eight of those in the sample name chocolate? (Round your answer to 4 decimal places.) Probability (c) What is the probability eight or more name chocolate? (Round your answer to 4 decimal places.) Probability
Answers
a) The expected number of people who would name chocolate in the sample is approximately 6.30. b) The probability of exactly eight people naming chocolate is given by \(P(X = 8) = (14 C 8) (0.45^8) (1 - 0.45)^{(14 - 8)\)
c) The probability of eight or more people naming chocolate sum the probabilities of exactly eight, nine, ten, eleven, twelve, thirteen, and fourteen people naming chocolate
(a) To find the expected number of people who would name chocolate in the sample, we multiply the percentage of people who prefer chocolate by the sample size. In this case, 45% is equivalent to 0.45, so we calculate the expected number as 0.45 * 14 = 6.30. Rounding to two decimal places, we expect approximately 6.30 people in the sample to name chocolate.
(b) To calculate the probability of exactly eight people naming chocolate, we use the binomial probability formula. The formula is \(P(X = k) = (n C k) * p^k * (1 - p)^{(n - k)\), where n is the sample size, k is the number of successes (people naming chocolate), p is the probability of success (45% or 0.45), and (n C k) represents the number of combinations. Substituting the values, we have \(P(X = 8) = (14 C 8) * (0.45^8) * (1 - 0.45)^{(14 - 8)\). Evaluating this expression gives us the probability of exactly eight people naming chocolate.
(c) To find the probability of eight or more people naming chocolate, we sum the probabilities of exactly eight, nine, ten, eleven, twelve, thirteen, and fourteen people naming chocolate. Using the same binomial probability formula as before, we calculate the probabilities for each number of successes and add them together to obtain the probability of eight or more people naming chocolate.
Note: Without additional information about the distribution or assumptions, we assume that the survey results are representative of the population and that the responses are independent and identically distributed.
Learn more about probability here: https://brainly.com/question/31828911
#SPJ11
13. In one week, Andy delivered 114 newspapers.
The new pr
He delivered the same number of newspapers on Monday, Tuesday and Wednesday.
Work
On Thursday he delivered half the number of papers he had delivered on Monday.
He delivered 10 newspapers each day on Friday, Saturday and Sunday.
How many newspapers did he deliver on Tuesday?
Answers
Answer: 24
Step-by-step explanation:
Let x be the number of newspapers he derlivered on Tuesday.
3.5x+30=114
Then
3.5x=114-30=84
x=24
abc is a right triangle with ab=ac. bisector of <a meets bc at d. prove that bc = 2ad.
Answers
Answer:
Let ac=ab=5
With this, bc= 5√2
Step-by-step explanation:
So to find ad, Let ad be x
5√2=(2)(x)
(5√2/2)= x
This proves that bc=2ad

type the correct answer in the box. simplify the following expression into the form a bi, where a and b are rational numbers. ( 4 − i ) ( − 3 7 i ) − 7 i ( 8 2 i )
Answers
The final simplified expression is: -211/7i - 3/7
To simplify the given expression, let's work step by step:
(4 - i)(-3/7i) - 7i(8/2i)
First, let's simplify each multiplication:
(4 * -3/7i - i * -3/7i) - (7i * 8/2i)
Now, simplify further:
(-12/7i + 3/7i^2) - (56/2)
Remember that i^2 is equal to -1:
(-12/7i + 3/7(-1)) - (28)
Simplify the expression:
(-12/7i - 3/7) - 28
Combining like terms:
-12/7i - 3/7 - 28
Now, let's express the terms as a single fraction:
-12/7i - 3/7 - 196/7
Combine the numerators:
(-12 - 3 - 196)/7i - 3/7
Simplify further:
(-211)/7i - 3/7
The final simplified expression is:
-211/7i - 3/7
To know more about Expression related question visit:
https://brainly.com/question/28170201
#SPJ11
2. 118 A certain form of cancer is known to be found
in women over 60 with probability 0. 7. A blood test
exists for the detection of the disease, but the test is
not infallible. In fact, it is known that 10% of the time
the test gives a false negative (i. E. , the test incorrectly
gives a negative result) and 5% of the time the test
gives a false positive (i. E. , incorrectly gives a positive
result). If a woman over 60 is known to have taken
the test and received a favorable (i. E. , negative) result,
what is the probability that she has the disease?
Answers
the probability that a woman has cancer given that she has a negative test result is 0.964.
A certain form of cancer is known to be found in women over 60 with probability 0.7. A blood test exists for the detection of the disease, but the test is not infallible. In fact, it is known that 10% of the time the test gives a false negative and 5% of the time the test gives a false positive.
For a woman over the age of 60, the probability of having cancer is 0.7.
Let A be the occurrence of a woman having cancer, and let B be the occurrence of a woman receiving a favorable test result. We need to calculate the probability that a woman has cancer given that she has a negative test result.
Using Bayes’ theorem, we can calculate
P(A | B) = P(B | A) * P(A) / P(B).P(B | A) = probability of receiving a favorable test result if a woman has cancer = 0.9 (10% false negative rate).
P(A) = probability of a woman having cancer = 0.7.P(B) = probability of receiving a favorable test result = P(B | A) * P(A) + P(B | ~A) * P(~A).
The probability of receiving a favorable test result if a woman does not have cancer is P(B | ~A) = 0.05.
The probability of a woman not having cancer is P(~A) = 0.3.P(B) = (0.9 * 0.7) + (0.05 * 0.3) = 0.655.P(A | B) = (0.9 * 0.7) / 0.655 = 0.964.
Hence, the probability that a woman has cancer given that she has a negative test result is 0.964.
To know more about probability visit:
brainly.com/question/31828911
#SPJ11
what is the greatest common factor of 20x6y 40x4y2−10x5y5? 10x4y 10 x begin power 4 end power y 5x2y5 5 x squared y begin power 5 end power 5x4y 5 begin power 4 end power y 20x6y
Answers
The greatest common factor of \(20x^{6} y+40x^{4} y^{2} -10x^{5} y^{5}\) is \(10x^{4} y\) .
The greatest common factor of a set of numbers is defined as the largest number that divides all the numbers in that given set and leaves 0 as remainder in each case.
In the given expression
\(20x^{6} y+40x^{4} y^{2} -10x^{5} y^{5}\)
Applying Prime Factorization and Writing all the terms in the above expression as
\(20x^{6} y=10x^{4}y *2x^{2}\)
\(40x^{4} y^{2} =10x^{4} y*4y\)
\(10x^{5} y^{5} =10x^{4}y*xy^{4}\)
As we can see that \(10x^{4} y\) is common and greatest in all the terms .
Hence \(10x^{4} y\) is the Greatest common factor.
Therefore , the greatest common factor of \(20x^{6} y+40x^{4} y^{2} -10x^{5} y^{5}\) is \(10x^{4} y\) , the correct option is (a)\(10x^{4} y\).
The given question is incomplete , the complete question is
What is the greatest common factor of \(20x^{6} y+40x^{4} y^{2} -10x^{5} y^{5}\)
(a)\(10x^{4} y\)
(b)\(5x^{2} y^{5}\)
(c)\(5x^{4} y\)
(d)\(20x^{6} y\)
Learn more about Greatest Common Factor here https://brainly.com/question/207329
#SPJ4
Questions regarding Boundary Conditions Section 4-8) = 262, E2 = 18€, and the boundary has 5. Question 4.48 With reference to Fig. 4-19, E = *3 - y2 +226 a surface charge density Ps = 3.54 x 10-11 a. What is E,? b. What angle does Eą make with the z axis? - plane Figure 4-19 Application of boundary conditions at the interface between two dielectric media (Example 4-10). 6. Derived from Question 4.49 An infinitely long conducting cylinder of radius a (medium 2) has a surface charge density P The cylinder is surrounded by a dielectric (Er = 4, medium 1) that contains no free charges (that is to say p = 0 inside the dielectric). Defining 2 as the axis of the conducting cylinder, the electric field, E, inside the dielectric medium (whenra) is found as: Ersin - 0,.co a. What is the normal vector, f, to the surface of the inner conductor? b. What is the boundary condition at the surface of the conductor (medium 2)? c. What is the boundary condition in the dielectric (medium 1)? d. What is the surface charge density, Ps, at the surface of the conducting cylinder?Previous question
Answers
The normal vector, f, to the surface of the inner conductor is a unit vector in the radial direction, pointing away from the conductor.
a. The normal vector, f, to the surface of the inner conductor is a unit vector in the radial direction, pointing away from the conductor.
b. The boundary condition at the surface of the conductor (medium 2) is that the normal component of the electric field is equal to the surface charge density.
c. The boundary condition in the dielectric (medium 1) is that the tangential component of the electric field is equal to zero.
d. The surface charge density, Ps, at the surface of the conducting cylinder is P.
The complete question is:
An infinitely long conducting cylinder of radius a (medium 2) has a surface charge density P. The cylinder is surrounded by a dielectric (Er = 4, medium 1) that contains no free charges (that is to say p = 0 inside the dielectric). Defining 2 as the axis of the conducting cylinder, the electric field, E, inside the dielectric medium (whenra) is found as: E = Er*sin(θ)/r.
a. What is the normal vector, f, to the surface of the inner conductor?
b. What is the boundary condition at the surface of the conductor (medium 2)?
c. What is the boundary condition in the dielectric (medium 1)?
d. What is the surface charge density, Ps, at the surface of the conducting cylinder?
Learn more about vector here
https://brainly.com/question/15709504
#SPJ4
Al dividir "D" entre "d" se obtuvo 12 de
cociente y 8 de residuo. Si: D + d = 203.
Hallar: D
Answers
El valor que satisface D es 188.
El modelo matemático será así:
D/d = 12(resto 8)
si escribimos 8 como resto de D, entonces:
(D-8) /d=12
D-8= 12d o se puede escribir D= 12d+8
luego sustituya D= 12d+8 por D+d= 203
D+d= 203
(12d +8) +d= 203
13d= 203-8
13d= 195
re=15
sustituir d=15 en D+d= 203
D+d= 203
D+15=203
D=203-15
D=188
Sobre el modelo matemáticoEl modelo matemático es una forma de interpretación humana al traducir o formular problemas existentes en forma matemática, de modo que el problema pueda resolverse utilizando las matemáticas.
El uso principal de los modelos matemáticos es ayudar a las personas a comprender los problemas y simplificarlos para que puedan resolverse.
, los siguientes son algunos de los usos que se obtienen al utilizar un modelo matemático, a saber:
Agrega velocidad, claridad y poder de ideas en un período de tiempo relativamente corto. La descripción del problema ocupa un lugar central. Obtener una comprensión o claridad del mecanismo en el problema. Se puede utilizar para predecir eventos que surgirán de un fenómeno o su expansión. Como base para la planificación y el control en la formulación de políticas, entre otros.Obtenga más información sobre el modelo matemático en
https://brainly.com/question/30517381
#SPJ1
Find the Volume of the shape below.
4 ft
2 ft
2 ft
Answers
Answer:
16 ft³
Step-by-step explanation:
4ft x 2ft x 2ft = 4ft x 4ft = 16 ft³
The measure of an angle is 39.9°. What is the measure of its complementary angle?
Answers
Answer:
50.1°
Step-by-step explanation:
What is an angle?An angle is a measure of a turn, measured in degrees or °. Angles are made up of two rays, making the sides of the angle.
What is a complementary angle?For two angles to be complementary, they need to add up to 90°.
If we now know that two complementary angles add up to 90°, we can use this equation to solve for the missing degree:
90 - 39.9 = 50.1To check, we can use this equation:
39.9 + 50.1 = 90Therefore, the measure of the missing angle is 50.1°.
531
x 47
Long multiplication :) please help
Answers
A wall has been built in such a way that the top row contains one block, the next lower row contains 3 blocks, the next lower row contains 5 blocks, and so on, increasing by two blocks in each row. How many rows high is the wall if the total number of blocks used was 900 ?
Answers
Answer:
The answer is 30 ROWS.
Step-by-step explanation:
Please give brainlyest

discuss any two advantages of superposition theorem
compared to other circuit theorms
Answers
The advantages of the superposition theorem compared to other circuit theorems are its simplicity and modularity in circuit analysis, as well as its applicability to linear circuits.
Superposition theorem is a powerful tool in circuit analysis that allows us to simplify complex circuits and analyze them in a more systematic manner. When compared to other circuit theorems, such as Ohm's Law or Kirchhoff's laws, the superposition theorem offers several advantages. Here are two key advantages of the superposition theorem:
Simplicity and Modularity: One major advantage of the superposition theorem is its simplicity and modular approach to circuit analysis. The theorem states that in a linear circuit with multiple independent sources, the response (current or voltage) across any component can be determined by considering each source individually while the other sources are turned off. This approach allows us to break down complex circuits into simpler sub-circuits and analyze them independently. By solving these individual sub-circuits and then superposing the results, we can determine the overall response of the circuit. This modular nature of the superposition theorem simplifies the analysis process, making it easier to understand and apply.
Applicability to Linear Circuits: Another advantage of the superposition theorem is its applicability to linear circuits. The theorem holds true for circuits that follow the principles of linearity, which means that the circuit components (resistors, capacitors, inductors, etc.) behave proportionally to the applied voltage or current. Linearity is a fundamental characteristic of many practical circuits, making the superposition theorem widely applicable in real-world scenarios. This advantage distinguishes the superposition theorem from other circuit theorems that may have limitations or restrictions on their application, depending on the circuit's characteristics.
It's important to note that the superposition theorem has its limitations as well. It assumes linearity and works only with independent sources, neglecting any nonlinear or dependent sources present in the circuit. Additionally, the superposition theorem can become time-consuming when dealing with a large number of sources. Despite these limitations, the advantages of simplicity and applicability to linear circuits make the superposition theorem a valuable tool in circuit analysis.
To learn more about superposition theorem visit : https://brainly.com/question/25329462
#SPJ11
Ben rolls a number cube 50 times. He records the result of each roll in the table below. RESULTS OF ROLLING NUMBER CUBE Outcome 1 2 3 4 5 6 Frequency 7 6 5 11 10 11 Based on the data, which statement is true? Ben will roll an even number about 250 times if the number cube is rolled 500 times. Ben will roll an even number about 220 times if the number cube is rolled 500 times. Ben will roll an even number about 700 times if the number cube is rolled 1,000 times. Ben will roll an even number about 560 times if the number cube is rolled 1,000 times.
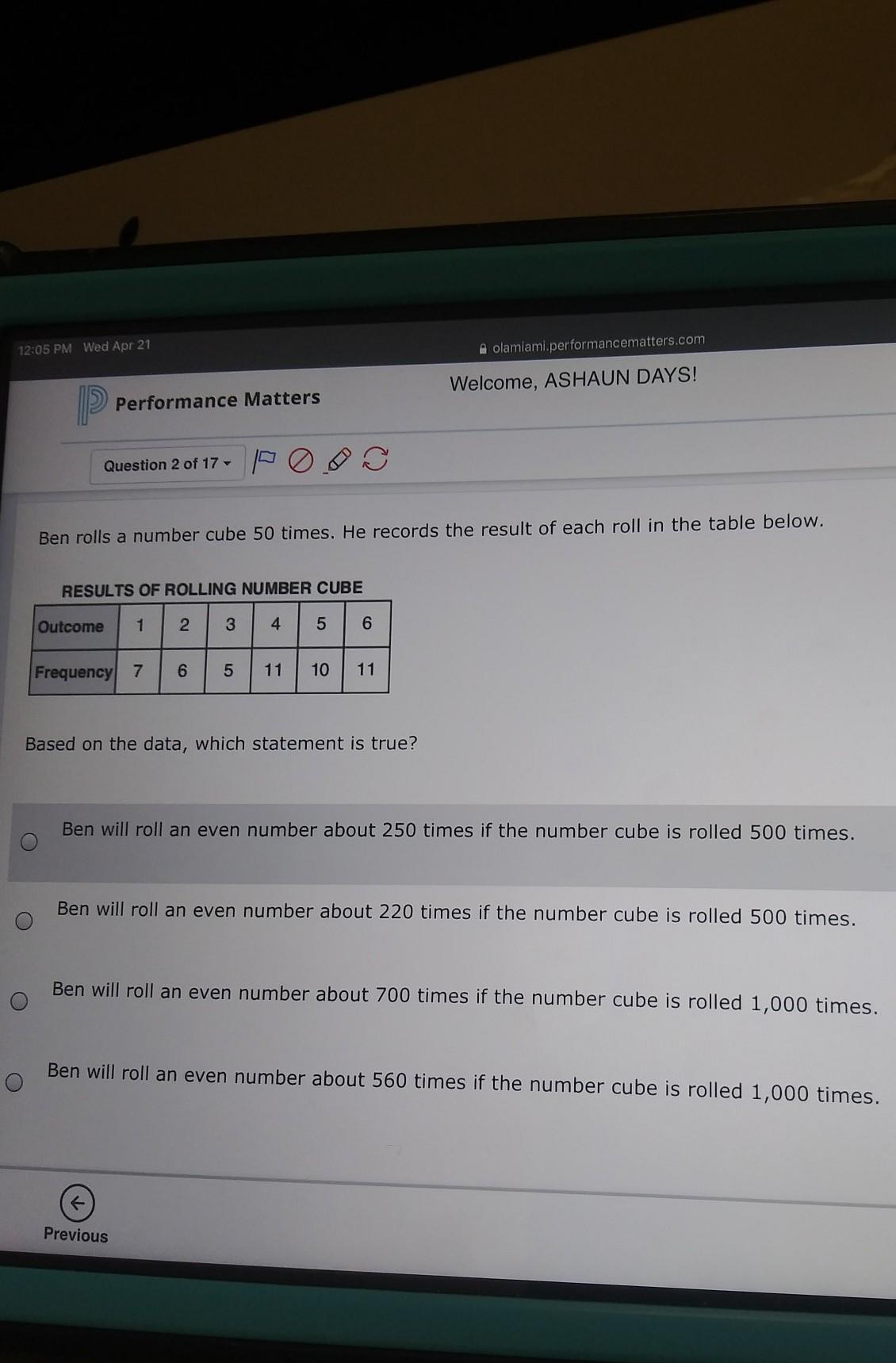
Answers
Answer:Ben will roll an even number about 560 times if the number cube is rolled 1,000 times.
Step-by-step explanation:
compare the row for 20 degrees and the row 70 degrees in the right triangle table. what is the same? what is different?

Answers
The row for 20 degrees and the row for 70 degrees in the right triangle table have the same values, but in reverse order.
How to explain the informationSpecifically, the sine, cosine, and tangent of 20 degrees are the same as the cosine, sine, and tangent of 70 degrees, respectively. The same holds true for their reciprocals, the cosecant, secant, and cotangent.
It should be noted that to complete the row for 35 degrees in the right triangle table, we can use the same ratios as for the complementary angle of 55 degrees, but in reverse order. Specifically:
The adjacent leg ÷ hypotenuse ratio for 35 degrees is equal to the opposite leg ÷ hypotenuse ratio for 55 degrees, which is 0.819.
Learn more about triangles on
https://brainly.com/question/17335144
#SPJ1
A fair coin is tossed 12 times. Which of the following outcomes (i, ii, iii, or iv) is most likely?
(i) H T H T H T H T H T H T
(ii) H T T H H T T H T H H T
(iii) H H H H H H H H H H H H
(iv) T T T H T H H H H T H H
A. (i) because there are an equal number of heads and tails.
B. (ii) because there are an equal number of heads and tails but in a random order
C. (iii) because heads are just as likely as tails
D. (iv) because you won’t necessarily get the same number of heads and tails with a fair coin
E. They are all equally likely.
Answers
Answer:
I want to say that it is E
Step-by-step explanation:
Well in terms of probability there is a 50% chance the coin will land heads and a 50% chance the coin will land tails. Since probability isn't definite you can never really get a precise number of each side. the most you could do is predict/guess
The most likely outcome is: E. They are all equally likely.
Each individual toss of a fair coin has an equal probability of being a heads or tails, regardless of what the previous tosses were. Therefore, all of the outcomes listed are equally likely. The order in which the heads and tails occur does not affect the probability of the overall outcome.
So, even though (i) has an equal number of heads and tails in an alternating pattern and (iii) has all heads, they are both equally likely to occur. The same goes for (ii) and (iv), which have an equal number of heads and tails but in a random order.
Therefore, The most likely outcome is: E. They are all equally likely.
To know more about outcomes refer here:
https://brainly.com/question/30882384#
#SPJ11
giúp mìn vs mngggggg

Answers
Answer:
136.99
Step-by-step explanation:
Đây là một câu hỏi dễ chỉ cần sử dụng máy tính
Find the exact values of x and y.

Answers
Answer:
x = 13 unitsy = 18.4 units
Step-by-step explanation:
from the angles we understand that it is an isosceles right triangle, therefore x is also 13, we find y with the Pythagorean theorem
y = √(13² + 13²)
y = √(169 + 169)
y = √338
y = 18.38 (you can round to 18.4)

Answer:
x = 13 , y = 18.38
Step-by-step explanation:
p.s. There is two ways to answer it.
In Triangle,
if there is a right angle, other angles are the same.
It the angles are the same, the two sides are the same.
So, x = 13
By the Converse of the Pythagorean Theorem , these values make the triangle a right triangle.
(hypotenuse)² = (side of right triangle)² + (other side of right triangle)²
(hypotenuse)² = 13² + 13²
(hypotenuse)² = 169 + 169
(hypotenuse)² = 338
hypotenuse = 18.38
so y = 18.38
which of the following calculations is not derived from the confidence interval? question content area bottom part 1 choose the correct answer below. a. difference between the limits, 2e b. the population mean, c. the margin of error, e d. the point es
Answers
Among the following, the population mean u = (upper confidence limit) + (lower confidence limit) is not derived from the confidence interval.
A confidence interval is defined as the range of values that we observe in our samples and for which we expect to find the value that accurately reflects the population.
In frequentist statistic, a confidence interval is a range of estimates for an unknown parameter.
To find a confidence level for a data set by taking half of the size of the confidence interval, multiplying it by the square root of the sample size and then dividing by the sample standard deviation.
Confidence level refers to the percentage of probability,or certainty, that the confidence interval would contain the true population parameter when you draw a random sample many times. The most common confidence levels are 90%, 95% and 99%.
To know more about confidence interval here
https://brainly.com/question/22424026
#SPJ4
define a regular $n$-pointed star to be the union of $n$ line segments $p 1p 2, p 2p 3,\ldots, p np 1$ such that the points $p 1, p 2,\ldots, p n$ are coplanar and no three of them are collinear, each of the $n$ line segments intersects at least one of the other line segments at a point other than an endpoint, all of the angles at $p 1, p 2,\ldots, p n$ are congruent, all of the $n$ line segments $p 1p 2, p 2p 3,\ldots, p np 1$ are congruent, and the path $p 1p 2, p 2p 3,\ldots, p np 1$ turns counterclockwise at an angle of less than 180 degrees at each vertex. there are no regular 3-pointed, 4-pointed, or 6-pointed stars. all regular 5-pointed stars are similar, but there are two non-similar regular 7-pointed stars. how many non-similar regular 1000-pointed stars are there?
Answers
The number of non-similar 1000-pointed stars is
\($\frac{1000-600-2}{2}= \boxed{199}.$\)
If we join the adjacent vertices of the regular \($n$\)-star, we get a regular \($n$\)\(-gon\). We number the vertices of this \($n$\)\(-gon\) in a counter clockwise direction: \($0, 1, 2, 3, \ldots, n-1.$\)
A regular \($n$\)-star will be formed if we choose a vertex number m where \($0 \le m \le n-1$\), and then form the line segments by joining the following pairs of vertex numbers:\($(0 \mod{n}, m \mod{n}),$ $(m \mod{n}, 2m \mod{n}),$ $(2m \mod{n}, 3m \mod{n}),$ $\dots,$ $((n-2)m \mod{n}, (n-1)m \mod{n}),$ $((n-1)m \mod{n}, 0 \mod{n}).$\)
If \($\gcd(m,n) > 1$\), then the star degenerates into a regular \($\frac{n}{\gcd(m,n)}$-gon\) or a (2-vertex) line segment if \($\frac{n}{\gcd(m,n)}= 2$\). Therefore, we need to find all $m$ such that \($\gcd(m,n) = 1$.\)
Note that \($n = 1000 = 2^{3}5^{3}.$\)
\(Let $S = \{1,2,3,\ldots, 1000\}$, and $A_{i}= \{i \in S \mid i\, \textrm{ divides }\,1000\}$. The number of $m$'s that are not relatively prime to $1000$ is: $\mid A_{2}\cup A_{5}\mid = \mid A_{2}\mid+\mid A_{5}\mid-\mid A_{2}\cap A_{5}\mid$ $= \left\lfloor \frac{1000}{2}\right\rfloor+\left\lfloor \frac{1000}{5}\right\rfloor-\left\lfloor \frac{1000}{2 \cdot 5}\right\rfloor$ $= 500+200-100 = 600.$\)
\(Vertex numbers $1$ and $n-1=999$ must be excluded as values for $m$ since otherwise a regular n-gon, instead of an n-star, is formed.\)
The cases of a 1st line segment of (0, m) and (0, n-m) give the same star. Therefore we should halve the count to get non-similar stars.
Therefore, the number of non-similar 1000-pointed stars is
\($\frac{1000-600-2}{2}= \boxed{199}.$\)
\(Note that in general, the number of $n$-pointed stars is given by $\frac{\phi(n)}{2} - 1$ (dividing by $2$ to remove the reflectional symmetry, subtracting $1$ to get rid of the $1$-step case), where $\phi(n)$ is the Euler's totient function.\) \(It is well-known that $\phi(n) = n\left(1-\frac{1}{p_1}\right)\left(1-\frac{1}{p_2}\right)\cdots \left(1-\frac{1}{p_n}\right)$, where $p_1,\,p_2,\ldots,\,p_n$ are the distinct prime factors of $n$.\) \(Thus $\phi(1000) = 1000\left(1 - \frac 12\right)\left(1 - \frac 15\right) = 400$, and the answer is $\frac{400}{2} - 1 = 199$.\)
To know more about vertex numbers visit brainly.com/question/1689812
#SPJ4
Please show all work and not just the answers.

Answers
Answer:
(-1, 6)
Step-by-step explanation:
Midpoint formula:
xm = (x1 +x2)/2ym = (y1+y2)/2For G(-7, 3) and H(5, 9) the midpoint:
((-7+5)/2, (3+9)/2) = (-1, 6)Answer:
(-1,6)
Step-by-step explanation
use the midpoint formula:
(x 1 + x2 /2 , y1 + y2/2)
(-7+ 5 /2, 3+ 9 /2)
after simplfying
(-1,6)
Find 3/8(3/4+5/6)−1/2. Write your answer as a fraction in simplest form.
Answers
which equation justifies why 27 1 3 is equivalent to the cube root of 27?
Answers
The equation that justifies why\(27^{(1/3)}\) is equivalent to the cube root of 27 is:\(27^{(1/3)} = (27^{1)^{(1/3)}} = 27^{(1/3)}\)
The definition of cube rootThe cube root symbol is represented by the number "3". In the square root case, only the root symbol—also known as a radical—was employed. Therefore, the cube root of different numbers can be symbolically represented as follows: 5 divided by its cube = 3. 11 has a cube root of 311 and so on.
What does a cube of 3 inches mean?The cube root of three is the same as the number 1.442224957031. The cube root of three has the radical representations 33 and 31/3. " denotes the square root.
The cube root formula aids in computing the cube root of any given number that is represented by the symbol in radical form. It can be determined by first determining the number's prime factorization and then using the cube root formula. Assume that x is any number such that it equals y, y, and y.
To know more about Cube Root visit:
brainly.com/question/30038389
#SPJ1
please help me again

Answers
The polynomial that shows that the left side is rising and the right side is falling is: Option D: -2x⁷ + ¹/₂x⁶ - 8x⁵ + 3x⁴ + 2x³ - 5x² + x - 7
How to find the end behavior of a polynomial?The end behavior of a polynomial function is defined as the behavior of the graph of f(x) as x approaches positive infinity or negative infinity. The degree and the leading coefficient of a polynomial function determine the end behavior of the graph.
Now, we are told that the left side is rising and the right side is falling. This means that both beginning and the end terms will have a negative sign attached to them.
The only option that shows both first and last terms having negative numbers is option D.
Read more about Polynomial End behavior at: https://brainly.com/question/1365136
#SPJ1
Please help me it’s a drag and drop

Answers
step 2) multiply all terms in equation 1 by -3
step 3) multiply all terms in equation 2 by 5
step 4) add the sum of the equations together to eliminate x
Last year you mowed grass and shoveled snow for 12 houses. You earned $225 for each lawn you mowed
and $200 for each house you shoveled for a total of $2600. How many lawns did you mow? How many
driveways did you shovel?
Answers
1800 lawns were mowed. 800 driveways were shoveled.
What is equation?A formula that expresses the connection between two expressions on each side of a sign. Typically, it has a single variable and an equal sign. Like this: 2x - 4 Equals 2. In the above example, the variable x exists. The definition of an equation in algebra is a mathematical statement that demonstrates the equality of two mathematical expressions.
Given Data
Let mowed grass be x
Let shoveled snow be y
Last year you mowed grass and shoveled snow for 12 houses
x + y = 12
y = 12 -x
You earned $225 for each lawn you mowed and $200 for each house you shoveled for a total of $2600.
225x + 200y = 2600
Equating value of y
225x + 200(12-x) = 2600
225x + 2400 - 200x = 2600
225x - 200x = 2600 - 2400
25x = 200
x = 8
For value of y,
y= 12 -x
y = 12 - 8
y = 4
Lawn mowed = 225(8)
Lawn mowed = 1800
Shoveled snow = 200(4)
Shoveled snow = 800
1800 lawns were mowed. 800 driveways were shoveled.
To learn more about equation, visit:
https://brainly.com/question/10413253
#SPJ13
write the reciprocal of the following numbers.
Number: 7/10. Reciprocal______
Number: 1/2. Reciprocal______
Number: 5. Reciprocal_______
Answers
Answer:
7/10 = 10/7
1/2 = 2/1
5 = 1/5
Step-by-step explanation:
The reciprocal is the flip of a fraction. 1/2 = 2/1
For a whole number (like 5) you put it over 1 (5/1) and then flip it (1/5)
Have a nice day! :)
Make me brainliest.
pls help reward brainleist




Answers
Answer:
number 1: {0,-6) number 2: f(-2)=25 number 3: x=±10 number 4:B, or x=-2, x=3
number 5:36 i really hope this helps! have a good day!
Step-by-step explanation:
1: 2x^2+12x +0=0
this is how you set it up
next, you have to find the a,b,and c. This is my personal favorite way of doing this.
a=2 b=12, c=0
you plug it in to the quadratic formula which is
-b±√b^2-4ac/2a
(-12)±√(12)^2-4(2)(0)/2(2)
next you have to simplify
-12±√144-0/4
take the square root of 144
-12±12/4-
then, find the solutions of them
-12+12=0
0/4=0
x=0
we are not done yet
-12-12=-24
-24/4
x=-6
your solutions are 0,-6, which is C
2: it is giving us x, which is -2
plug in -2 to the right side of the equation.
2(-2)^2-4(-2)+9
2(4)-8+9
8-8+9
f(-2)=9
3: this one is fairly simple
x^2=100
take the square root of each side
x=±10
4: you have to replace y for 0 in this one
x^2-x-6=0
all you have to do is factor it out, and it turns into
(x+2)(x-3)
then turn these so they equal 0
x+2=0, x-3=0
x=-2 x=3
your answer would be B
5: this one is fairly simple too
the formula to completing the square is (b/2)^2
you plug in b, which is 12
12/2=6
6^2=36
you would add 36 to each side.
Answer:
7) {0, -6}
1) 25
2) x= ±10
3) x= 3, -2
4) 36
5) 225/4
6) x = -3±\(2\sqrt{3}\)
Step-by-step explanation:
1) 2x^2 -4x + 9
2(-2)^2 - 4(-2) + 9
8+ 8 + 9
25
