I NEED HELP PLEASE THIS IS DUE IN 14 MINUTES. I’LL MARK YOUR ANSWER BRAINLIEST!!!
1: Louisa (L) is five years less than three times Brie’s age. Together, their age totals 43. How old is Louisa?
2: If the perimeter of the rectangular field is 84, where the length is x + 7 and the width is 3x - 1, determine the value of x.
3: If the perimeter of the rectangular field is 84, where the length is x + 7 and the width is 3x - 1. Determine the width.
4: If the perimeter of the rectangular field is 84, where the length is x + 7 and the width is 3x - 1. Determine the length.
Answers
Answer:
1) 12
2) x=9
3) width=26
4) length=16
Step-by-step explanation:
Related Questions
The product of two numbers is 161 , one of number is 7,find the other number.
Answers
let the other number be " n "
now, according to above condition :
n × 7 = 161 n = 161 ÷ 7 n = 23therefore, the other number would be 23.
From a point P, the bearings of two points Q and R are N67°W and N23°E respectively. If the bearing of R from Q
is N68° E and PQ = 150m, calculate PR
Answers
Answer:
He does S3423163 miles plus average calculas. Auto-correct
Step-by-step explanation:
The demand equation for a popular brand of fruit drink is given by the equation:
Qx=10-5px+0.001M + 10Py
where:
Qx= monthly consumption per family in liters
Px= price perlite of the fruit drink =$2.00
M= median annual family income =$20,000
Py= price per liter of a competing brand of fruit drink = $2.50.
1. Interpret parameter estimates.
2. Calculate the monthly consumptioliterslitres) of the fruit.
3. Suppose that the median annual family income increased to ¢30,000. How does this change your answer to part (b)?
4. Determine the demand function and the inverse demand function.
Answers
Answer:
Parameter estimates
The coefficient for Px (-5) suggests that there is an inverse relationship between the price of the fruit drink and the quantity demanded. In other words, as the price of the drink increases, the quantity demanded decreases.
The coefficient for M (0.001) suggests that there is a positive relationship between the median annual family income and the quantity demanded. In other words, as the median income increases, the quantity demanded also increases.
The coefficient for Py (10) suggests that there is a positive relationship between the price of the competing brand of fruit drink and the quantity demanded for this brand. In other words, as the price of the competing brand increases, the quantity demanded for this brand also increases.
Step-by-step explanation:
To calculate the monthly consumption of the fruit drink, we plug in the given values into the demand equation,
Qx = 10 - 5(2) + 0.001(20,000) + 10(2.5)
Qx = 10 - 10 + 20 + 25
Qx = 45 liters per family per month.
Therefore, the monthly consumption of the fruit drink per family is 45 liters.
If the median annual family income increased to $30,000, then the new monthly consumption of the fruit drink per family can be calculated as follows,
Qx = 10 - 5(2) + 0.001(30,000) + 10(2.5)
Qx = 10 - 10 + 30 + 25
Qx = 55 liters per family per month.
Therefore, the monthly consumption of the fruit drink per family would increase from 45 liters to 55 liters per family per month.
To determine the demand function, we need to solve for Qx in terms of the other variables,
Qx = 10 - 5Px + 0.001M + 10Py
Qx - 10Py = 10 - 5Px + 0.001M
Qx = (10 - 5Px + 0.001M) / 10Py
Therefore, the demand function is:
Qx = (10 - 5Px + 0.001M) / 10Py
To find the inverse demand function, we need to solve for Px in terms of Qx.
Qx = 10 - 5Px + 0.001M + 10Py
5Px = 10 - Qx - 0.001M - 10Py
Px = (10 - Qx - 0.001M - 10Py) / 5
Therefore, the inverse demand function is,
Px = (10 - Qx - 0.001M - 10Py) / 5
If a firm’s total fixed costs are $11,639, total revenues are $28,200, and profit is $4,776, what must the firm’s total variable cost be?
Answers
Answer:
Step-by-step explanation:
PLEASE HELP ME THE QUESTION IS ON THE PICTURE!!!!!

Answers
But not sure about the rest, sorry
Help help help math math

Answers
Answer:
gradient M = 4
Step-by-step explanation:
pick any two pairs
M= change in Y / change in X
considering the last pairs
3--1/0--1=4✓
considering first pair
-1--5/-1--2 is also 4✓
I hope it helps
Suppose the prices of a certain model of new homes are normally distributed with a mean of 150,000. Use the 68-95-99.7 rule to find the percentage of buyers who paid between $149,000 and $151,000 if the standard deviation is $1000
Answers
The percentage of buyers is approximately 68.26% of buyers of new houses paid between \($149,000\) and \($151,000\) .
We are given that the prices of the new homes are normally distributed with a mean of \($150,000\) and a standard deviation of $1000.
Using the 68-95-99.7 rule, we know that: approximately 68% of the data falls within one standard deviation of the mean approximately 95% of the data falls within two standard deviations of the mean, approximately 99.7% of the data falls within three standard deviations of the mean.
In order to determine the proportion of customers who spent between $149,000 and , we must first determine the z-scores for these values:
z1 = (149,000 - 150,000) / 1000 = -1 z2 = (151,000 - 150,000) / 1000 = 1
Now, we can determine the proportion of data that falls between z1 and z2 using the z-table or a calculator. The region to the left of z1 is 0.1587, and the area to the left of z2 is 0.8413, according to the z-table. Thus, the region bounded by z1 and z2 is:
0.8413 - 0.1587 = 0.6826
We can get the percentage of consumers who spent between by multiplying this by 100% is \($149,000\) and \($151,000\):
0.6826 x 100% = 68.26%
Therefore, the standard deviation of customers who paid between is \($149,000\) and \($151,000\) for this model of new homes.
For such more questions on standard deviation
https://brainly.com/question/30557671
#SPJ11
5.2 × _______ = 5.2 whats the answer
Answers
Answer:
1
Step-by-step explanation:
Emma and her aunt shared 9 oranges each, how many oranges did they each get?
Answers
Answer:
4 and 1/2.
Step-by-step explanation:
There are 9 oranges, so there are not enough for both to get a whole amount.
They will split the last one into half, so they has 4 and 1/2 oranges each.
Answer: 4 and 1/2
P.S Can I get a Brainliest? Thanks!
Solve 2-3 cos x=5+3 cosx for 0° ≤ 180°
Answers
The equation 2-3cos(x) = 5+3cos(x) has no solution in the range of 0° to 180°.
1. Start with the given equation: 2-3cos(x) = 5+3cos(x).
2. Subtract 3cos(x) from both sides to isolate the constant term: 2-3cos(x) - 3cos(x) = 5.
3. Combine like terms: 2-6cos(x) = 5.
4. Subtract 2 from both sides: -6cos(x) = 3.
5. Divide both sides by -6: cos(x) = -1/2.
6. To find the solutions for cos(x) = -1/2 in the range of 0° to 180°, we need to determine the angles where cos(x) equals -1/2.
7. These angles are 120° and 240°, as cos(120°) = cos(240°) = -1/2.
8. However, the given equation states that 2-3cos(x) equals 5+3cos(x), which is not satisfied by cos(x) = -1/2.
9. Therefore, the equation 2-3cos(x) = 5+3cos(x) has no solution in the range of 0° to 180°.
For more such questions on equation, click on:
https://brainly.com/question/17145398
#SPJ8
For each function, find f(−x) and −f(x) and then determine whether it is even, odd, or neither. Justify your answer. f(x)=2x^2-7x+10
Answers
The function f(x) = 2x² - 7x + 10 is an odd function.
f(-x) = 2(-x)² - 7(-x) + 10
= 2x² + 7x + 10
-f(x) = -[2x²- 7x + 10]
= -2x² + 7x - 10
To determine whether the function f(x) = 2x² - 7x + 10 is even, odd, or neither, we compare f(-x) and -f(x).
1. f(-x) = 2x² + 7x + 10
2. -f(x) = -2x² + 7x - 10
To determine if f(-x) = -f(x) (even function), we substitute -x for x in f(x) and check if the equation holds.
1. f(-x) = 2x² + 7x + 10
= f(x) (not equal to -f(x))
Since f(-x) is not equal to -f(x), the function is not even.
Next, to determine if f(-x) = -f(x) (odd function), we substitute -x for x in f(x) and check if the equation holds.
2. -f(x) = -2x² + 7x - 10
= -(2x² - 7x + 10)
= -(f(x))
Since -f(x) is equal to -(f(x)), the function is odd.
For more such questions on odd, click on:
https://brainly.com/question/2263958
#SPJ8
Height of redwood trees is normally distributed, with a mean of 360 feet, and a standard deviation of 10 feet. Using this information and a z-score table, find the percentile for a redwood tree that is 375 feet tall. a. 13thb. 95th c. 80thd. 93rd
Answers
The percentile for a redwood tree that is 375 feet tall would be 93rd percentile. This is because the z-score of 1.5 (375-360/10) corresponds to a percentile of 93.
Step 1: Find z-score
z-score = (375-360)/10 = 1.5
Step 2: Find percentile
Using a z-score table, the percentile corresponding to a z-score of 1.5 is 93.
Therefore, the percentile for a redwood tree that is 375 feet tall is 93rd percentile.
The percentile of a redwood tree that is 375 feet tall can be determined using a z-score table. The z-score of a data point is the difference between the data point and the mean, divided by the standard deviation. In this case, the z-score is (375-360)/10 = 1.5. This z-score corresponds to a percentile of 93 on a z-score table. Therefore, the percentile for a redwood tree that is 375 feet tall is 93rd percentile. This means that 93% of redwood trees are shorter than 375 feet tall. It also means that only 7% of redwood trees are taller than 375 feet tall. This information can be used to compare the size of a particular redwood tree to other redwood trees.
Learn more about z score here
https://brainly.com/question/15016913
#SPJ4
I NEED HELP WITH THIS QUESTION PLEASE NO LINKS!!!

Answers
Answer:
\( \longmapsto - 3 \frac{3}{8} - \frac{7}{8} \\ = - \frac{27}{8} - \frac{7}{8} \\ = \frac{ (- 27 - 7)}{8} \\ = \frac{( - 34)}{8} \\ = \frac{ (- 34) \div 2}{(8) \div 2} \\ = \frac{ - 17}{4} \\ = \boxed{ - 4 \frac{1}{4} }✓\)
- 4¼ is the right answer.Ninety-nine is what percent of 150?
Answers
Answer:
66
Step-by-step explanation:
Answer:
66
Step-by-step explanation:
Simon started for school at 8:30 he got there 15minuter later. what time did he get to school
Answers
Answer:
8:45
Step-by-step explanation:
XD 8:30+15 mins =8:45
In a certain board game, a player rolls two fair six-sided dice until the player rolls doubles (where the value on each die is the same). The probability of rolling doubles with one roll of two fair six-sided dice is What is the probability that it takes three rolls until the player rolls doubles?
(a) (1/5)^3
(b) (5/6)^3
(c) (1/5) (5/6)^3
(d) (1/6) (5/6)^2
(e) (5/6) (1/6)^2
Answers
The probability of not rolling doubles on one roll of two fair six-sided dice is 5/6.
Hence, the probability of rolling doubles is 1/6. The probability of not rolling doubles in three rolls is (5/6)^3. So, the probability of rolling doubles on the third roll is 1 - (5/6)^3. This is the same as (1/6) (5/6)^2. So the correct answer is (d) (1/6) (5/6)^2.
The probability of rolling a specific number on one fair six-sided die is 1/6.
In this problem, we are looking for the probability of rolling doubles (i.e. getting the same number on both dice) in three rolls.
The probability of not rolling doubles in one roll is 5/6 (since there are five outcomes that are not doubles, out of a total of 6 possible outcomes).
The probability of not rolling doubles in three rolls is (5/6)^3, which represents the chance of not rolling doubles in three independent rolls, each with a 5/6 probability of not rolling doubles.
To find the probability of rolling doubles in three rolls, we subtract the probability of not rolling doubles in three rolls from 1:
P(rolling doubles in three rolls) = 1 - (5/6)^3 = (1/6) (5/6)^2
So, the correct answer is (d) (1/6) (5/6)^2.
To Know More about Probability
https://brainly.com/question/13604758
#SPJ4
which statement is true of the Y value of function I would ask equals -2 is greater than the Y value function be when I ask equals negative to the Y value function a 1X equals -2 is less than the Y value a function be one x was -2
Answers
The statement "the Y value of function I would ask equals -2 is greater than the Y value function be when I ask equals negative to the Y value function a 1X equals -2 is less than the Y value a function be one x was -2" is true.
Given, two functions y = -2f(x) = 1/x
To determine whether the statement "the Y value of function I would ask equals -2 is greater than the Y value function be when I ask equals negative to the Y value function a 1X equals -2 is less than the Y value a function be one x was -2" is true or false, we need to find the value of Y for both functions when x = -2.
Substituting x = -2 in the functions we get:I would ask y = -2(-2) = 4f(-2) = 1/(-2) = -1/2Therefore, the Y value of the function I would ask is greater than the Y value function be when I ask equals negative to the Y value function a 1X equals -2 is less than the Y value a function be one x was -2. Hence, the given statement is true.
Therefore, the statement "the Y value of function I would ask equals -2 is greater than the Y value function be when I ask equals negative to the Y value function a 1X equals -2 is less than the Y value a function be one x was -2" is true.
For more questions on value .
https://brainly.com/question/843074
#SPJ8
The graph of a cube root function f is shown.
The graph of g is a vertical shrink by a factor of 1/2 of the graph of f. Graph the function g.

Answers
A graph of the cube root function g(x) = 1/2x³ is shown in the image below.
What is a dilation?In Geometry, a dilation is a type of transformation which typically transforms the dimension (size) or side lengths of a geometric object, without affecting its shape.
This ultimately implies that, the dimension (size) or side lengths of the dilated geometric object would be stretched or shrunk depending on the scale factor that is applied.
When the parent cube root function f(x) = x³ is vertically shrunk by a scale factor of 1/2, the transformed function g(x) is given by;
g(x) = kf(x)
g(x) = 1/2f(x)
g(x) = 1/2x³.
Read more on dilation and scale factor here: brainly.com/question/4421026
#SPJ1

Determine whether the following statement is true or false.
Generally, the goal of an experiment is to determine the effect that the treatment will have on the response variable.
Answers
True, Generally, the goal of an experiment is to determine the effect that the treatment will have on the response variable.
What does a response variable in an experiment mean?
Response Continuum In an experimental investigation, this is the result that is assessed after manipulating the explanatory variable; it is also referred to as the dependent or outcome variable.
Its value is expected or its variation is explained by the explanatory variable.
What other name would you give the answer variable?
The term "dependent variable" is one more typical moniker for the response variable. The response variable is frequently referred to as just "the response" for short.
There are several more terms for the predictor variables, including "explanatory variables," "independent variables," "predictors," and "regressors."
Learn more about the response variable
brainly.com/question/14662435
#SPJ4
if cos 0 =8/17, what is sin 0?
Answers
Answer:
sin=15/17
Step-by-step explanation:
Use the definition of sine to find the value of
sin (0)
sin (0) = opp/hyp
THEN
Substitute in the known values.
sin (0) = 15/17
The following table represents a relation.x y−3 00 −25 −311 −2Does the table represent y as a function of x?Why or why not?

Answers
Given the table:
x y
-3 0
0 -2
5 -3
11 -2
Let's determine if the table represents y as a function of x.
When we say y as a function of x, it means the y value depends on x values.
For a relation to be a function, there must be one value of y for every unique value of x. This means one value of x must not appear twice.
From the given table, no value of x is repeated. Hence, we can say there is one value of y for every value of x.
Therefore, the table represents a function because there are no x-values with more than one y-value.
ANSWER:
Yes, because there are no x-values with more than one y-value.
Complete the table and fill in the last

Answers
Answer:
Its will be 2/3
Step-by-step explanation:
hope it helps you
Answer:
3/5…...........….........
34+35? :)))) answer immediately
Answers
Answer:
69
Step-by-step explanation:
30+30=60
4+5=9
60+9=69!
You have a choice between going to an in-state college where you would pay $3000 per year for tuition and an out-of-state college where the tuition is $6500 per year. The cost of living is much higher at the in-state college, where you can expect to pay $1000 per month in rent, compared to $450 per month at the other college. Assuming all other factors are equal, which is the less expensive choice on an annual (12-month) basis?
Answers
Answer:
The less expensive choice is the out-of-state college
Step-by-step explanation:
in-state-college: 1000(12)+3000=15000
out-of-state-college:450(12)+6500=11900
consider the verizon data. find a 95% ci for the ratio of medians. estimate the percent bias (relative to the standard error) and compare with the results for the ratio of means
Answers
95% confidence interval for the ratio of medians is a range of values that we are confident contains the true population ratio, with a specified level of confidence.
A confidence interval is a range of values that we are confident contains the true population parameter, with a specified level of confidence. In this case, we are looking at the ratio of medians in the Verizon data and finding a 95% confidence interval for the ratio.
Let's say the sample median for the first data set is M1 and the sample median for the second data set is M2. The standard error for M1 and M2 can be calculated using the formula for the standard error of the median.
Next, we use the formula for a confidence interval for the ratio of medians:
=> (M1/M2) +/- (Z * SE(M1/M2)),
where Z is the critical value from a standard normal distribution for a 95% confidence level.
The percent bias is the difference between the estimated value and the true value, divided by the true value and expressed as a percentage. In this case, we will calculate the percent bias of the confidence interval for the ratio of medians relative to the standard error.
Finally, we compare the results for the ratio of medians with the results for the ratio of means. This comparison can give us an idea of the difference in the level of accuracy and precision between the two estimates.
Complete Question:
Consider the Verizon data. find a 95% confidence interval for the ratio of medians. estimate the percent bias (relative to the standard error) and compare with the results for the ratio of means
To know more about confidence interval here.
https://brainly.com/question/24131141
#SPJ4
Renata is purchasing a condominium for $125,000. She wants to put down a down payment of 20%. Select all the true statements. The proportion that represents the down payment is 20100=125,000 20 100 = 125 , 000 x . The down payment is $25,000. The proportion that represents the down payment is 20100=125,000 20 100 = x 125 , 000 . The down payment is $50,000. The down payment is 15 1 5 of the cost of the house.
Answers
The correct options are -
The proportion that represents the down payment is : 20/100 x 125000.The down payment is $25,000What is down payment?When something is bought on credit, an initial payment is made in the form of a down payment.
Given is that Renata is purchasing a condominium for $125,000. She wants to put down a down payment of 20%.
We can calculate the amount she is putting in down payment as -
{x} = 20% of 125000
{x} = 20/100 x 125000
{x} = 20 x 1250
{x} = 25000
Therefore, the correct options are -
The proportion that represents the down payment is : 20/100 x 125000.The down payment is $25,000To solve more questions on functions & equations, visit the link-
https://brainly.com/question/29014197
#SPJ9
convert from rectangular to spherical coordinates. (use symbolic notation and fractions where needed. give your answer as a point's coordinates in the form (*,*,*).)(5, π/8, 0) ->
Answers
The spherical coordinates of the given rectangular coordinates are (10, 0, 60).
The cartesian coordinate or rectangular coordinates describes the location of a point in space using an ordered triple where each coordinate represents a distance. The spherical coordinate system describes the location of a point in space using an ordered triple where coordinate describes one distance and two angles. In the spherical coordinate system, a point is represented by the ordered triple (ρ, θ, φ).
The equations which are used to convert from rectangular coordinates to spherical coordinates are:
ρ^2=x^2+y^2+z^2
tan〖θ= y/x〗
φ=arccos〖z/√(x^2+y^2+z^2 )〗
The given rectangular coordinates are (5√3, 0, 5). Hence,
ρ^2=〖(5√3)〗^2+0^2+5^2 ≈ 100
ρ ≈ √100 ≈ 10
tan〖θ= 0/(5√3)=0〗
θ= tan^(-1)0=0
φ=arccos〖5/√(〖(5√3)〗^2+0^2+5^2 )〗= arccos 5/10=arccos0.5 ≈ 60
Note: The question is incomplete. The complete question probably is: Convert from rectangular to spherical coordinates. (Use symbolic notation and fractions where needed. Give your answer as a point's coordinates in the form (*,*,*). (5√3, 0, 5)
Learn more about Spherical coordinates:
https://brainly.com/question/4465072
#SPJ4
Rajani is carrying 9.725 kg of vegetables and Mamta is carrying 8.50 kg of vegetables. Who is carrying more and how much?
Answers
To find out how much more vegetables Rajini is carrying, you have to SUBTRACT Mamta’s amount from it.
So: 9725 g - 8500 g = 1025 g
and 1025 g = 1.025 kg
Answer: Rajini is carrying 1.025 kg more vegetables than Mamta.
Answer:
Step-by-step explanation:
let Rajani be carrying r = 9.725kg
let Mamata be carrying m = 8.500kg
difference = r - m = 9.725 - 8.500 = 1.225kg
hence Rajani is carrying 1.225kg more than Mamata
The tree diagram represents an experiment consisting of two trials
P(A)=

Answers
Based on the parameters in the question, the value of probability P(A) is 0.60
How to determine the probability?The given parameters from the tree diagram are:
Probability of event A: P(A only) = 0.6Probability of event A: P(A and C) = 0.3Probability of event A: P(A and D) = 0.7The probability is calculated using the following probability formula
P(A) = P(A and D) + P(A and C)
Substitute the known values in the above equation
P(A) = 0.6 * 0.7 + 0.6 * 0.3
Evaluate the products
P(A) = 0.42 + 0.18
Evaluate the sum
P(A) = 0.60
Hence, the value of the probability of A is 0.60
Read more about probability at:
brainly.com/question/795909
#SPJ1
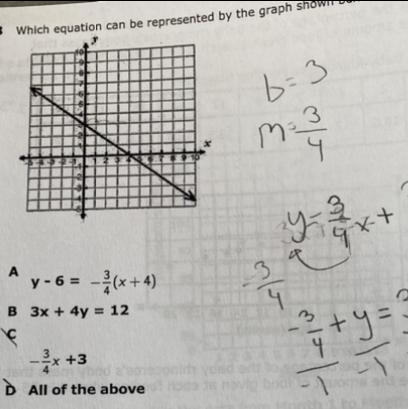
which equation can be represented by the graph below (alegbra help)
Answers
Answer:
Option D) All of the above.
Step-by-step explanation:
Given the two points on the graph:
Let (x1, y1) = (0, 3)
(x2, y2) = (4, 0)
Substitute these values into the slope formula:
m = (y2 - y1)/(x2 - x1)
m = (0 - 3)/(4 - 0)
m = -¾
Next, we need to determine the y-intercept, which is the point on the graph where it crosses the y-axis. Looking at the graph, the line crosses at point (0, 3), which happens to be one of the points we used in solving for the slope. Its y-coordinate is the value of b.
Therefore, the linear equation of the graph is y = -¾ + 3, which matches Option C.
Test Option A:We need to determine whether Option A is also a correct answer. Transform the equation into its slope-intercept form:
y - 6 = -¾(x + 4)
y - 6 = -¾x - 3
y - 6 + 6 = -¾x - 3 + 6
y = -¾x + 3 ⇒ also matches the given equation. Therefore, Option A is also correct.
Test Option B:To find out whether Option B is also a correct answer, transform its equation into its slope-intercept form, y = mx + b:
3x + 4y = 12
3x - 3x + 4y = -3x + 12
4y = -3x + 12
Divide both sides by 4:
\(\frac{4y}{4} = \frac{-3x + 12}{4}\)
y = -¾ + 3 ⇒ also matches the given equation. Therefore, Option B is also correct.
Thus, the correct answer is Option D) All of the above.