Answers
Answer:
irratrrational Numbers
whole
real
Step-by-step explanation:
Related Questions
y=9x
y= 2x+49
plz help

Answers
Answer:
(7, 63)
Step-by-step explanation:
X= 7 and Y=63
Hope this helps!!!
Answer:
(7,63)
Step-by-step explanation:
first subsititute the y into the second equation making it 9x=2x+49
second you can solve that to get x=7
next plug in x=7 into the first equation y=9(7)
9*7= 63
therefore y =63
and x= 7
hope this makes sense
Billy has 5 1/4 yards of wire if he uses for is 4 7/8 yards to make a fence how much would he have left
Answers
Reasoning: 5.25 – 4.875 = 0.375, transferred back into a fraction would be 3/8
olivia can run 100 yards in 15 seconds. what is her speed in miles per hour? round to the nearest whole nimber
Answers
14 mph
Step-by-step explanation:
13.636364
is what you get by doing
100/15 then you get 6.6666......7
after that you multiply that by 3600 because thats how many seconds in that hour.
Then you get 24000 and transfer it to miles and get 13.636364 and you round it and get 14mph
PLEASE MARK MY ANSWER BRAINLIEST
Write three rational numbers between −1 /5 and 1 /2
Answers
Answer:
-1/10, 2/10, and 4/10
Step-by-step explanation:
A rational number is a number that is in the form of p/q, where p and q are integers, and q is not equal to 0.
First, what is the lcm of 5 and 2? the lcm is 10, because that is the lowest number than can be divided separately by 5 and 2 and the results would still be a whole number.
We now need to find 3 rational numbers between -2/10 and 5/10. It's easy now that I've explained it, right?
-1/10, 2/10, and 4/10 are between -1/5 and 1/2 and are integers with the given explanation.
Hope this helps.
the average car can go 25 miles on one gallon of gas. You can write an equation to show the relationship between the amount of gas you buy and how far you can travel
Answers
Answer:
Step-by-step explanation:
the inword
write 0.00086 in standard form
Answers
Answer:
8.6 × 10-4
Step-by-step explanation:
All numbers in scientific notation or standard form are written in the form m × 10n, where m is a number between 1 and 10 ( 1 ≤ |m| < 10 ) and the exponent n is a positive or negative integer. Therefore, the decimal number 0.00086 written in scientific notation is 8.6 × 10-4 and it has 2 significant figures.
In inferential statistics, we calculate statistics of sample data to:.
Answers
In inferential statistics, we calculate statistics of sample data to estimate the characteristics of the entire population from which the sample was taken. The process involves drawing inferences about a population from a random sample of data taken from that population.
The sample statistics are used to estimate the parameters of the population. To make an inference, we use a hypothesis test or confidence interval based on the sample statistics. The key to inferential statistics is random sampling, which allows us to make generalizations about the population based on the characteristics of the sample.
In order to ensure that the sample is representative of the population, we use a variety of sampling techniques, including simple random sampling, stratified sampling, cluster sampling, and systematic sampling.
Each of these techniques has its own advantages and disadvantages, and the choice of technique depends on the characteristics of the population being studied and the research questions being asked.
Once we have a representative sample, we use statistical methods to draw conclusions about the population. This allows us to make predictions and to test hypotheses about the population with a high degree of confidence.
To know more about Statistics visit :
https://brainly.com/question/32237714
#SPJ11
PLEASE HELP!!!!
Quadrilateral ABCD is similar to quadrilateral EFGH. What is the value for x, the length
of side CD?
A-10
B-16
C-14
D-18

Answers
-》D
Answer:
D 18
Step-by-step explanation:

PLEASE HELP 75 POINTS

Answers
Answer:
A because a prism is the only solid they can be used in that way
The price of a computer component is decreasing at a rate of 10% per year. State whether this decrease is linear or exponential. If the component costs $100 today, what will it cost in three years?
Answers
the computer component will cost approximately $72.90 in three years.
The decrease in the price of the computer component at a rate of 10% per year indicates an exponential decrease. This is because a constant percentage decrease over time leads to exponential decay.
To calculate the cost of the component in three years, we can use the formula for exponential decay:
\[P(t) = P_0 \times (1 - r)^t\]
Where:
- \(P(t)\) is the price of the component after \(t\) years
- \(P_0\) is the initial price of the component
- \(r\) is the rate of decrease per year as a decimal
- \(t\) is the number of years
Given that the component costs $100 today (\(P_0 = 100\)) and the rate of decrease is 10% per year (\(r = 0.10\)), we can substitute these values into the formula to find the cost of the component in three years (\(t = 3\)):
\[P(3) = 100 \times (1 - 0.10)^3\]
\[P(3) = 100 \times (0.90)^3\]
\[P(3) = 100 \times 0.729\]
\[P(3) = 72.90\]
to know more about exponential visit:
brainly.com/question/29631075
#SPJ11
Write an equation of the line with the given slope, m, and y-intercept (0,b), m=7, b=5
Answers
Answer: y = 7x + 5 (maybe, please make sure, I'm very doubtful of myself sometimes)
Step-by-step explanation:
1. With the given numbers, m is slope, so 7 is the slope and b is y-intercept, and 5 is the y-int in this case.
2. This is hinting that the equation is in slope intercept form, which is y = mx + b.
3. Since y = mx + b is the formula, then it means y = 7x + 5 is the likely answer
Use the pigeonhole principle to prove each of the following statements about numbers: (a) Given any seven integers, there will be two that have a difference divisible by 6. (b) Given any five integers, there will be two that have a sum or difference divisible by 7.
Answers
The pigeonhole principle states that if there are more pigeons than pigeonholes, then at least one pigeonhole must contain more than one pigeon. We can apply this principle to prove the following statements:
(a) Given any seven integers, there will be two that have a difference divisible by 6.
We can divide the integers into six pigeonholes based on their remainders when divided by 6: {0}, {1}, {2}, {3}, {4}, and {5}. Since there are seven integers, by the pigeonhole principle, at least two integers must belong to the same pigeonhole. If two integers belong to the same pigeonhole, then their difference will be divisible by 6.
(b) Given any five integers, there will be two that have a sum or difference divisible by 7.
We can divide the integers into six pigeonholes based on their remainders when divided by 7: {0}, {1}, {2}, {3}, {4}, {5}, and {6}. Since there are five integers, by the pigeonhole principle, at least two integers must belong to the same pigeonhole. If two integers belong to the same pigeonhole, then their sum or difference will be divisible by 7.
Note that if the two integers have the same remainder when divided by 7, then their difference will be divisible by 7. If they have different remainders, then their sum will be divisible by 7.
Visit here to learn more about pigeonhole principle brainly.com/question/31687163
#SPJ11
is 9 x 1/9 greater than one , less than one or equal to one
Answers
Answer:
equal to 1
Step-by-step explanation:
9 x 1/9 = 9/9 = 1
If my answer is incorrect, pls correct me!
If you like my answer and explanation, mark me as brainliest!
-Chetan K
Answer:
equal to one
Step-by-step explanation:
9 times 1/9 is one
Someone can help me with this

Answers
Answer:
hrhrh4vguaiwjnbbbhhhhh
Step-by-step explanation:
jrrjbbdjhtvb4sjjfjjjejsjuhfhrbdhksopapdkbrbhfhhxizidjjdjkkwkalqlpqpwkjdhbdnMsmnznxbbfjsjddheb5vgguyy5
write a program that draws a pyramid of circles based on user input 2.19.5
Answers
Here is the program that draws a pyramid of circles based on user input. The user is asked to input the number of rows for the pyramid. Each row has an increasing number of circles as you go down the pyramid.```# Importing turtle module import turtle# Function to draw circledef draw_circle(radius): turtle.circle(radius)
# Function to move turtle to specified coordinatesdef move_turtle(x, y): turtle.penup() turtle.goto(x, y) turtle.pendown()# Main function def main(): # User input for number of rows in pyramid rows = int(input("Enter the number of rows for the pyramid: ")) x = -50 y = 0 radius = 10 distance = 30 for i in range(rows): for j in range(i+1): draw_circle(radius) move_turtle(x, y) x += distance x = -50 y -= distance turtle.done()# Calling main function if __name__ == '__main__': main()```
The program starts by importing the turtle module, which is used to draw the circles. The program then defines two functions: `draw_circle()` and `move_turtle()`. The `draw_circle()` function takes a radius as an argument and uses the turtle module to draw a circle with that radius.
To know more about program visit:
https://brainly.com/question/30613605
#SPJ11
SOMEONE TELL ME WHAT THIS IS PLEASE ( much appreciated if you do help with this question )

Answers
Answer:
6x^8 y^5
Step-by-step explanation:
What is the slope of the line that passes through the points (-4, 8)(−4,8) and (-14, 8) ?(−14,8)? Write your answer in simplest form.
Answers
Answer:
Slope is 0
Step-by-step explanation:
To find it subtract the x and y values of both points.
-4 + 14 = 10
8 - 8 = 0
Now since the y value is 0
That means the whole slope is 0
The slope is 0!
Suppose a triangle has sides a, b, and c, and let e be the angle opposite the side of length a. If cose < 0, what must be true? O A. a² + b² = ² O B. b² + c²> a² O c. b² + 2² ²
Answers
In the given triangle the statement that holds true is \(b^2+c^2 < a^2\). Therefore, the option (c) is the correct option.
What are cosine formulas?In the cosine formulas, the cosine (cos) function is discussed. Consider a right-angled triangle with one acute angle, x. The cosine formula is cosx = (adjacent side) / (hypotenuse), where "adjacent side" refers to the side adjacent to angle x and "hypotenuse" refers to the longest side of the triangle.
As per cosine rule fore given \($\triangle$\)ABC:
\($\cos \theta=\frac{b^2+c^2-a^2}{2 b c}$$$\)
According to the question;
For a given \($\triangle$\)ABC;
cos e < 0.
Therefore, \(\quad \frac{b^2+c^2-a^2}{2 b c} < 0 \\\)
\(b^2+c^2 < a^2\)
To know more about cosine formula visit:
https://brainly.com/question/17171751
#SPJ9
solve for x. Math question.

Answers
Answer:
x - 13+7=180
x=13+7-180 =160
What is a danger that would stop us from using an AED?.
Answers
Automated External Defibrillator(AEDs) administer an electrical shock. So it is dangerous to use n a victim who is lying on a conductive surface.
In the given question we have to explain what is a danger that would stop us from using an AED.
AEDs can be hazardous to use in damp settings, endangering the patient or the person supplying care. When treating the cardiac arrest sufferer, you must be especially careful because AEDs administer an electrical shock. When submerged in water, never use an AED.
Do not use an AED on a victim who is laying on conductive material. If other people are close to conductive items like metal bleachers or sheet metal, they could also get shocked.
To learn more about Automated External Defibrillator(AEDs) link is here
brainly.com/question/4472635
#SPJ4
....................
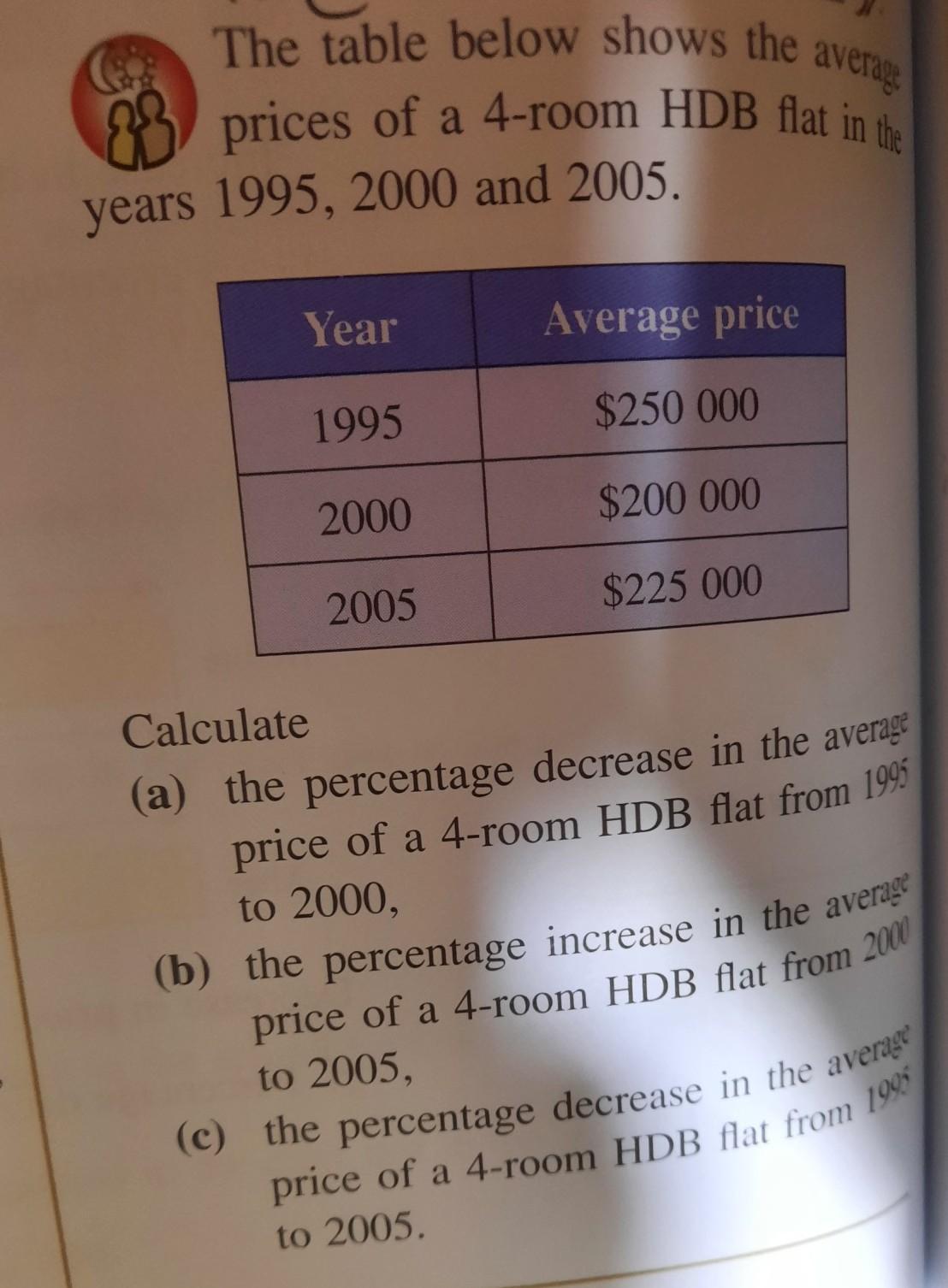
Answers
................................................i dont know
suppose that f(0)=−3 and f′(x)≤8 for all values of x. use the mean value theorem to determine how large f(4) can possibly be. answer: f(4)≤
Answers
The largest value that f(4) can possibly be is 29.
The mean value theorem states that for a function f(x) that is continuous on the closed interval [a, b] and differentiable on the open interval (a, b), there exists a number c in the open interval (a, b) such that:
f(b) - f(a) = f'(c)(b - a)
In this case, we are given that f(0) = -3 and that f'(x) ≤ 8 for all values of x. To determine how large f(4) can possibly be, we can use the mean value theorem with a = 0 and b = 4:
f(4) - f(0) = f'(c)(4 - 0)
Substituting the given values:
f(4) - (-3) = f'(c)(4)
f(4) + 3 = 4f'(c)
Since f'(x) ≤ 8 for all values of x, we can say that f'(c) ≤ 8. Therefore:
f(4) + 3 ≤ 4f'(c) ≤ 4(8) = 32
Therefore, we have:
f(4) ≤ 32 - 3 = 29
Learn more about the differentiation here:
brainly.com/question/954654
#SPJ11
Which list is in order from least to greatest
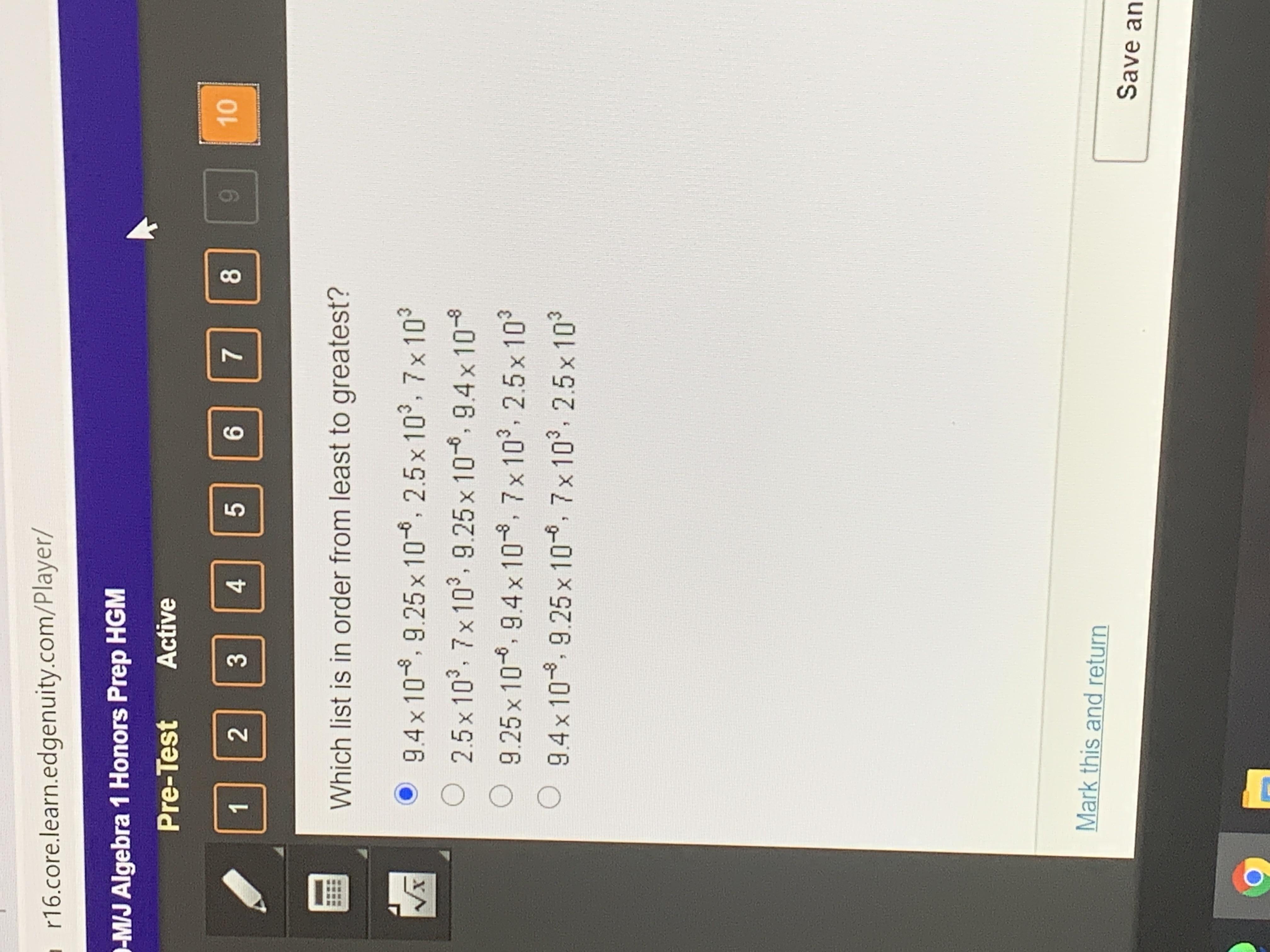
Answers
The correct answer to this question is A. 9.4 x \(10^{-8}\), 9.25 x \(10^{-6}\), 2.5 x \(10^{3}\), 7 x
Explanation:
These numbers are written in scientific notation. In this system, the exponent shows the number of spaces the period has been moved to make the number shorter. Additionally, a positive exponent shows the number has a certain number of digits to the right, while a negative exponent shows the number has digits to the left. In this way, the numbers presented can be converted as:
9.4 x \(10^{-8}\) = 0.000000094 (Exponent indicates eight spaces to the left)
9.25 x \(10^{-6}\) = 0.00000925 (Exponent indicates six spaces to the left)
2.5 x \(10^{3}\) = 2500 (Exponent indicates three spaces to the right)
7 x \(10^{3}\) = 7000 (Exponent indicates three spaces to the right)
given the function of f(x)=-4x(x 3)(x-4), determine the local behavior
Answers
To determine the local behavior of the function f(x) = -4x(x^2)(x-4), we can examine the signs and multiplicity of the factors involved.
This will help us identify the intervals where the function is increasing or decreasing, as well as locate any local extrema (maximum or minimum points).
Let's analyze the factors of the function:
x:
The factor x appears once, so it changes signs at x = 0.
It is a linear factor, so it has a slope of 1 and passes through the origin.
(x^2):
The factor (x^2) appears with an even power, which means it is always non-negative.
It is a quadratic factor, so its graph is a parabola that opens upwards.
(x-4):
The factor (x-4) appears once, so it changes signs at x = 4.
It is a linear factor, so it has a slope of 1 and passes through the point (4, 0).
Now, let's consider the local behavior of the function:
At x = 0:
The factor x is zero, so f(0) = 0.
Since (x^2) and (x-4) are non-zero, their effect does not change the sign of the overall function.
Therefore, we have a potential local minimum at x = 0.
Between x = 0 and x = 4:
The factor x remains non-zero and positive in this interval.
The factor (x-4) changes signs from negative to positive.
The overall function f(x) will be negative in this interval.
At x = 4:
The factor (x-4) is zero, so f(4) = 0.
Since x and (x^2) are non-zero, their effect does not change the sign of the overall function.
Therefore, we have a potential local maximum at x = 4.
For x > 4:
The factor (x-4) remains non-zero and positive in this interval.
The factor x changes signs from positive to negative.
The overall function f(x) will be positive in this interval.
Based on this analysis, we can summarize the local behavior of the function f(x) = -4x(x^2)(x-4) as follows:
There is a potential local minimum at x = 0.
There is a potential local maximum at x = 4.
The function is negative between x = 0 and x = 4.
The function is positive for x > 4.
Please note that these conclusions are based on the factors and their signs, and additional analysis might be necessary to confirm the nature of the local extrema.
Learn more about function here:
https://brainly.com/question/30721594
#SPJ11
How many positive integers have exactly three proper divisors (positive integral divisors excluding itself), each of which is less than 50
Answers
The total number of positive integers with exactly three proper divisors and each divisor less than 50 is \(7+18=\boxed{25}$.\)
To have exactly three proper divisors, a number must be of the form \(p_1^2$ or $p_1p_2$\), where \($p_1$\) and \($p_2$\) are prime numbers.
For the case of \(p_1^2$,\) there are only 7 prime numbers less than 50. So, there are 7 possible numbers of the form \(p_1^2$.\)
For the case of \($p_1p_2$\), we can choose 2 prime numbers from the 7 available prime numbers, which can be done in \($\binom{7}{2} = 21$\) ways. However, we must exclude the numbers that are squares of primes, which are already counted in the previous case. There are 3 such numbers: \(2^2$, $3^2$,\)and $5^2$. So, there are \($21-3=18$\) possible numbers of the form \(p_1p_2$.\)
Therefore, the total number of positive integers with exactly three proper divisors and each divisor less than 50 is \(7+18=\boxed{25}$.\)
Learn more about positive integers
https://brainly.com/question/18380011
#SPJ4
34.2 million Americans, or 10.5% of the population, had diabetes in the year 2018. What is the probability that a randomly chosen person has diabete
Answers
The probability that a randomly chosen person has diabetes is approximately 10.45%.
The probability that a randomly chosen person has diabetes can be calculated by dividing the number of people with diabetes by the total population. Using the given data, we have:
Total population = 100%Probability of having diabetes = 10.5%Number of people with diabetes = 34.2 million
To find the probability of a randomly chosen person having diabetes, we divide the number of people with diabetes by the total population as follows:
Probability of having diabetes = (Number of people with diabetes / Total population) x 100%
= (34.2 million / 327 million) x 100%
= 0.1045 or 10.45%
Therefore, the probability that a randomly chosen person has diabetes is approximately 10.45%.
Know more about probability here:
https://brainly.com/question/30034780
#SPJ11
What’s the area of the shape

Answers
21.2 because you use the area of a circle formula which is pi times r squared and divide it by four to get each quarter and then multiply by three because there are 3 quarters of the circle.
Select all ratios equivalent to 3:6.
A: 6:3
B: 24:48
C: 5:9
Answers
Answer:
B. 24:48
Step-by-step explanation:
3:6 is equivalent to 1:2 which is also equivalent to 24:48.
II The small capillaries in the lungs are in close contact with the alveoli. A red blood cell takes up oxygen during the 0.5s that it squeezes through a capillary at the surface of an alveolus. What is the diffusion time for oxygen across the 1-um thick membrane separating air from blood? Assume that the diffusion coefficient for oxygen in tissue is .2x10^-11m^2/s Give your answer to 1 significant figure.
Answers
The diffusion time of the red blood cell to take oxygen through the membrane is 25uS.
The small capillaries in the lungs are in close contact and it takes a red blood cell 0.5 seconds to squeeze through the capillary.
The diffusion time for the oxygen across the 1 um thick membrane separating the air is given by,
t = x²/2D
Where,
t is the diffusion time,
x is the thickness of the membrane,
D is the diffusion coefficient.
Putting values,
t = (1 x 10⁻⁹)²/2 x 2 x 10⁻¹¹
t = 10⁻⁷/4
t = 25 x 10⁻⁹ seconds.
t = 25 uS.
so, the diffusion time is 25uS.
To know more about Diffusion, visit,
https://brainly.com/question/94094
#SPJ4
Write the ratio as a fraction in lowest terms. (3.4)/(2.2)
Answers
The ratio 3.4/2.2 can be expressed as a fraction in lowest terms as 17/11.
To find the fraction in lowest terms, we need to simplify it by dividing both the numerator and denominator by their greatest common divisor (GCD). In this case, the GCD of 17 and 11 is 1, as there are no common factors other than 1. Dividing 17 and 11 by 1 gives us the fraction 17/11, which is already in its simplest form.
In the given ratio 3.4/2.2, the numerator is 3.4 and the denominator is 2.2. To convert it into a fraction, we can express both the numerator and denominator as whole numbers by multiplying them by a power of 10. In this case, we multiply both 3.4 and 2.2 by 10 to get 34 and 22, respectively. The ratio then becomes 34/22. To simplify this fraction, we find the greatest common divisor of 34 and 22, which is 2. Dividing both the numerator and denominator by 2 gives us the fraction 17/11, which is the simplest form of the ratio.
Learn more about ratio here:
https://brainly.com/question/8482466
#SPJ11
