I’ll give BRAINLIEST if correct pls need ASAP
Part A: given the function
g(x) = |x+3| describe the graph of the function including the vertex domain and range
Part B: if the parent function
f(x) = |x| is transformed to
h(x) = |x| - 2 what Transformation occurs from
f(x) to h(x) how are the vertex and range of h(x) affected
Answers
Answer:
A) The graph of function g(x) is V-shaped and has the following properties:
The vertex is (-3, 0)The axis of symmetry is x = -3The domain is the set of all real numbers: (-∞, ∞)The range is [0, ∞)B) Translation of 2 units down.
Therefore:
The vertex is (0, -2)The range is [-2, ∞)Step-by-step explanation:
The absolute value parent function, f(x) = |x|, is defined as:
\(f(x)=\begin{cases}x \; &\text{if}\;x > 0\\0 \; &\text{if} \; x=0\\-x\; &\text{if}\;x < 0\end{cases}\)
Therefore:
The slope of the line where x > 0 is positive.The slope of the line where x < 0 is negative.Its graph is V-shaped and has the following properties:
The x-intercept and y-intercept are at the origin (0, 0).The vertex is at the origin (0, 0).The axis of symmetry is x = 0 (y-axis).The domain is the set of all real numbers: (-∞, ∞).The range is the set of all real numbers greater than or equal to 0: [0, ∞).Part AGiven absolute value function:
\(g(x)=|x+3|\)
The graph of function g(x) is the parent function f(x) translated 3 units to the left.
As the graph has only been translated horizontally, the domain and range are the same as the parent function.
Therefore, the graph of function g(x) has:
Vertex = (-3, 0)Domain = (-∞, ∞)Range = [0, ∞)Part BGiven absolute value functions:
\(f(x)=|x|\)
\(h(x)=|x|-2\)
The graph of function h(x) is the parent function f(x) translated 2 units down.
As the graph has been translated vertically, the domain is the same as the parent function, but the vertex and range are different.
The y-value of the vertex of h(x) is 2 less than f(x).Therefore, the vertex is (0, -2).The minimum value of range of h(x) is 2 less than f(x).
Therefore, the range is [-2, ∞).
Related Questions
I need help I can't figure this out
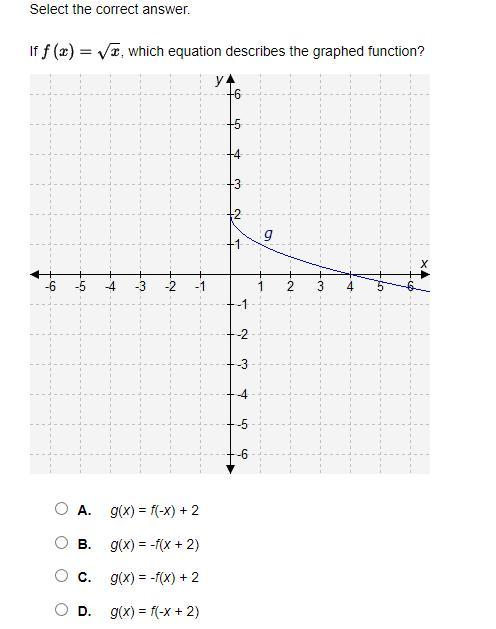
Answers
Answer:
C
Step-by-step explanation:
It can't be A since you can't have a negative inside a square root
It can't be B \(-\sqrt{x+2}\) since it would always be negative and the graph starts positive then turns negative at x=4
C makes since since the graph looks sort of like an upside down \(\sqrt{x}\) and has an intercept at y=2
It can't be D since after x=2 the inside of the square root would become negative and you can't have a negative inside of a square root
Jackson wrote different patterns for the rule subtract 5 select all the patterns he could have written
Answers
When Jackson wrote different patterns for the rule "subtract 5", the patterns that he could have written include
A. 27, 22, 17, 12, 7
D. 100, 95, 90, 85, 80
What is the expression regarding the pattern?It is important to note that an expression is simply used to show the relationship between the variables that are provided or the data given regarding an information. In this case, it is vital to note that they have at least two terms which have to be related by through an operator.
Some of the mathematical operations that are illustrated in this case include addition, subtraction, etc. In this case, when Jackson wrote different patterns for the rule "subtract 5", the patterns that he could have written include 27, 22, 17, 12, 7 and 100, 95, 90, 85, 80. In this cases, there are difference of 5.
Learn more about expressions on:
https://brainly.com/question/723406
#SPJ1
Complete question
Jackson wrote different patterns for the rule "subtract 5". Select all of the patterns that he could have written.
27, 22, 17, 12, 7
5, 10, 15, 20, 25
55, 50, 35, 30, 25
100, 95, 90, 85, 80
75, 65, 55, 45, 35
with expression 1. the options are, 2 factors, 3 factors, 2 terms, 3 terms.
with expression 2. the options are, 2 factors, 3 factors, 2 terms, 3 terms.
its a multiple choice question ;-;

Answers
Consider the expression 4(8x + 5)
Complete 2 descriptions of the parts of the expression.
1. The entire expression is the product of 2 factors.
1 factor is 42 factor is (8x + 5)2. On its own, (8x + 5) is a sum with 2 terms.
1 term is 8x2 term is 5Which proportion could you use to convert 96 inches to feet?
96 inches=____ feet

Answers
Answer:
8
Step-by-step explanation:
1 foot=12 in. So we can do 96/12=8.
PRE CALC HELP NEEDED

Answers
Answer:
\(\dfrac{5e^2}{2}\)
Step-by-step explanation:
Differentiation is an algebraic process that finds the slope of a curve. At a point, the slope of a curve is the same as the slope of the tangent line to the curve at that point. Therefore, to find the slope of the line tangent to the given function, differentiate the given function.
Given function:
\(y=x^2\ln(2x)\)
Differentiate the given function using the product rule.
\(\boxed{\begin{minipage}{5.5 cm}\underline{Product Rule for Differentiation}\\\\If $y=uv$ then:\\\\$\dfrac{\text{d}y}{\text{d}x}=u\dfrac{\text{d}v}{\text{d}x}+v\dfrac{\text{d}u}{\text{d}x}$\\\end{minipage}}\)
\(\textsf{Let\;$u=x^2}\)\(\textsf{Let\;$u=x^2$}\implies \dfrac{\text{d}u}{\text{d}x}=2x\)
\(\textsf{Let\;$v=\ln(2x)$}\implies \dfrac{\text{d}v}{\text{d}x}=\dfrac{2}{2x}=\dfrac{1}{x}\)
Input the values into the product rule to differentiate the function:
\(\begin{aligned}\dfrac{\text{d}y}{\text{d}x}&=u\dfrac{\text{d}v}{\text{d}x}+v\dfrac{\text{d}u}{\text{d}x}\\\\&=x^2 \cdot \dfrac{1}{x}+\ln(2x) \cdot 2x\\\\&=x+2x\ln(2x)\end{aligned}\)
To find the slope of the tangent line at x = e²/2, substitute x = e²/2 into the differentiated function:
\(\begin{aligned}x=\dfrac{e^2}{2}\implies \dfrac{\text{d}y}{\text{d}x}&=\dfrac{e^2}{2}+2\left(\dfrac{e^2}{2}\right)\ln\left(2 \cdot \dfrac{e^2}{2}\right)\\\\&=\dfrac{e^2}{2}+e^2\ln\left(e^2\right)\\\\&=\dfrac{e^2}{2}+2e^2\\\\&=\dfrac{5e^2}{2}\end{aligned}\)
Therefore, the slope of the line tangent to the graph of y = x²ln(2x) at the point where x = e²/2 is:
\(\boxed{\dfrac{5e^2}{2}}\)
Jim began a 145mile bicycle trip to build up stamina for a triathlon competition. Unfortunately, his bicycle chain broke, so he finished the trip walking. The whole trip took 7 hours. If Jim walks at a rate of 4 miles per hour and rides at 30 miles per hour, find the amount of time he spent on the bicycle.
Answers
The amount of time he spent on bicycle is 4.5 hours.
Given Jim began a 145 mile bicycle trip.
The whole trip took 7 hours.
Jim walks at a rate of 4 miles per hour and rides at 30 miles per hour.
speed = distance / time
time = distance / speed
ride:
d = distance ridden
t = d/30 (given from the problem)
walk:
t = (145 - d)/4 (given from problem)
total trip time:
7 = d/30 + (145 - d)/4.
7 = 4d/120 + 30(145 - d)/120
7×120 = 4d + 30(145 - d)
840= 4d +4350-30d
840 ₋ 4350 = ₋30d ₊ 4d
₋3510 = ₋26d
d = 3510/26
d = 135
d=135 then from here using the formula t = d / s we can solve
t=135/30 = 4.5 hours
hence the amount of time Jim spent on the bicycle is 4.5 hours.
Learn more about Speed, time and distance here:
https://brainly.com/question/17146782
#SPJ9
. The pet store salesman told Evan to feed his dog 8 ounces of food per day. The food is sold in pounds. How many pounds does Evan need to buy for 2 weeks of feeding his dog? (16 ounces = 1 pound)?
Answers
anyone else come on here and pretend to be smart?
Answers
Graph the solution to the equations below. y = 1 4 x + 2 and y = −2x −7
Answers
HELP IM IN K12 AND THERS MORE OF THESE

Answers
Help me help me , I will give brainliest

Answers
Answer:
All except the 3rd
Step-by-step explanation:
what the step for answer

Answers
Answer:
See explanations below
Step-by-step explanation:
What the step for answer
Given the nth terms of as sequence expressed as
Sins a ≥ 3, we can find the third term of the sequence
an = 2an-1 + an-2 - 2an-3
If a1 = 6 and a2 = 0 and a0 = 3
a3 = 2a2 + a1 - 2a0
a3 = 2(0) + 6 - 2(3)
a3 = 0 + 6 - 6
a3 = 0
If n = 4
a4 = 2a3 + a2 - 2a1
a4 = 2(0) + 0 - 2(6)
a4 = 0 + 0 - 12
a4 = -12
Find the area of the parallelogram

Answers
Answer:
1191 cm²
Step-by-step explanation:
Area of parallelogram = base X vertical height.
Call the vertical line h.
h/ sin 80 = 7/ sin 10
h = (7 sin 80) / sin 10
= 39.7.
Area of parallelogram = 30 X 39.7
= 1191 cm²
The Area of Parallelogram whose side length is 30 cm is 1,190.952 square cm.
Given:
Side length = 30 cm
Using Trigonometry
tan 80 = P / Base
5.6712 = P / 7
P = 39.6984 cm
Using the formula for Area of parallelogram
= Base x height
= 30 x 39.6984
= 1,190.952 square cm.
Therefore, the area is 1,190.952 square cm.
Learn more about Area of Parallelogram here:
https://brainly.com/question/9148769
#SPJ6
Akeem is carrying water in a bucket, but is unsure how many gallons it holds. He knows that the bucket and water weigh 32.49 pounds together. The bucket alone weighs 2.61 pounds and the water weighs 8.3 pounds per gallon. How many gallons of water is Akeem carrying? Add or divide?
Answers
Answer:
Step-by-step explanation:
8.3g+2.61=32.49
8.3g=29.88
g=3.6
If you know this please help

Answers
1) given
2) given
3) Definition of linear pair
4) If alternate interior angles are congruent, then the lines are parallel.
Find the amount accumulated after
investing a principal P for t years at an
interest rate compounded k times per year.
P = $1,500 r = 7% t=5 k = 4
Hint: A = P (1+)kt
A = $[?]
can someone pls help me with this?
Answers
The value or the amount accumulated after investing P = $1,500 at an annual interest rate of r = 7% for 5 years compounded 4 times per year, therefore; is A ≈ $2,122.2
What is a compound interest?A compound interest is a form of interest rate that is applied to both the principal and the interest accumulated in the previous period.
The specified parameters are;
P = $1,500, r = 7%, t = 5, k = 4
Where;
k = The number of payments per year = 4
P = The principal = $1,500
t = The number of years = 5 years
The formula for compound interest is presented as follows;
A = P·(1 + r/k)^(n × t)
Therefore;
A = 1500 × (1 + 0.07/4)^(4 × 5) ≈ 2,122.2
The amount of the investment after 5 years is therefore; A ≈ $2,122.2Learn more on compound interest here: https://brainly.com/question/17578515
#SPJ1
An analyst takes a random sample of 25 firms in the telecommunications industry and constructs a confidence interval for the mean return for the prior year. Holding all else constant, if he increased the sample size to 30 firms, how are the standard error of the mean and the width of the confidence interval affected
Answers
Answer:
The standard error decreases and the width of the confidence interval also decreases.
Step-by-step explanation:
The standard error of a distribution (E) is given as:
\(E=z_{\frac{\alpha}{2} }*\frac{\sigma}{\sqrt{n} }\)
Where n is the sample size, \(z_{\frac{\alpha}{2} }\) is the z score of he confidence and \(\sigma\) is the standard deviation.
The sample size is inversely proportional to the standard error. If the sample size is increased and everything else is constant, the standard would decrease since they are inversely proportional to each other. The confidence interval = μ ± E = (μ - E, μ + E). μ is the mean
The width of the confidence interval = μ + E - (μ - E) = μ + E - μ + E = 2E
The width of the confidence interval is 2E, therefore as the sample size increase, the margin of error decrease and since the width of the confidence interval is directly proportional to the margin of error, the width of the confidence interval also decreases.
Which of the following is true for the function f(x)=2cos(x2)
a. The period is π
b. The period is π2
c. The period is 2π
d. The period is 4π
e. The period is 2
Answers
Answer:
c. The period is 2π
Step-by-step explanation:
The period of a function is the smallest value of $p$ for which\( f(x+p) = f(x)\) for all x.
For the function f(x) = 2cos(x^2), we can see that f(x+2π) = f(x) for all x.
This is because the cosine function has a period of 2π. Therefore, the period of f(x) = 2cos(x^2) is \(\boxed{2\pi}\)
As the CAPS document outlines, the Content Specification and Content Clarification for Patterns, Functions, and Algebra shows sequenced mathematics content topics and a content area spread. In the Intermediate Phase, select one topic and report on the topic sequence and content area spread. Your report should demonstrate mathematics concepts and procedures’ hierarchical and logical progression.
Answers
Answer:
Step-by-step explanation:
In the Intermediate Phase of mathematics education, one topic that demonstrates a hierarchical and logical progression in patterns, functions, and algebra is the concept of "Linear Equations."
The topic of Linear Equations in the Intermediate Phase builds upon the foundation laid in earlier grades and serves as a stepping stone towards more advanced algebraic concepts. Here is an overview of the topic sequence and content area spread for Linear Equations:
Introduction to Variables and Expressions:
Students are introduced to the concept of variables and expressions, learning to represent unknown quantities using letters or symbols. They understand the difference between constants and variables and learn to evaluate expressions.
Solving One-Step Equations:
Students learn how to solve simple one-step equations involving addition, subtraction, multiplication, and division. They develop the skills to isolate the variable and find its value.
Solving Two-Step Equations:
Building upon the previous knowledge, students progress to solving two-step equations. They learn to perform multiple operations to isolate the variable and find its value.
Writing and Graphing Linear Equations:
Students explore the relationship between variables and learn to write linear equations in slope-intercept form (y = mx + b). They understand the meaning of slope and y-intercept and how they relate to the graph of a line.
Systems of Linear Equations:
Students are introduced to the concept of systems of linear equations, where multiple equations are solved simultaneously. They learn various methods such as substitution, elimination, and graphing to find the solution to the system.
Word Problems and Applications:
Students apply their understanding of linear equations to solve real-life word problems and situations. They learn to translate verbal descriptions into algebraic equations and solve them to find the unknown quantities.
The content area spread for Linear Equations includes concepts such as variables, expressions, equations, operations, graphing, slope, y-intercept, systems, and real-world applications. The progression from simple one-step equations to more complex systems of equations reflects a logical sequence that builds upon prior knowledge and skills.
By following this hierarchical progression, students develop a solid foundation in algebraic thinking and problem-solving skills. They learn to apply mathematical concepts and procedures in a systematic and logical manner, paving the way for further exploration of patterns, functions, and advanced algebraic topics in later phases of mathematics education.
2 1/2 + (345-206) - 3 1/3
Answers
Answer:
139 should be the answer
Step-by-step explanation:
find the quantity if v=5i-7j and w=3i+2j ||v||-||w||
Answers
\(\begin{cases} v=5i-7j\\\\ w=3i+2j \end{cases}\qquad \begin{cases} < \stackrel{a}{5}~~,~~\stackrel{b}{-7} > \\\\ < \stackrel{a}{3}~~,~~\stackrel{b}{2} > \end{cases}\qquad \qquad \stackrel{magnitude}{\sqrt{a^2 + b^2}} \\\\[-0.35em] ~\dotfill\\\\ ||v||~~ - ~~||w||\implies \sqrt{5^2+(-7)^2}~~ - ~~\sqrt{3^2 + 2^2}\implies \sqrt{74}-\sqrt{13} ~~ \approx ~~ 5\)
guys please help me i have 5 mins to finish this!

Answers
Answer:
the answer is 19.5
Step-by-step explanation:
im smart
HELP ASAP!!!!!!!!!!
What is the equation of the line that passes through the point (- 3, 1) and has a slope of 2/3?
Answers
Step-by-step explanation:
Equation of a line passing through a point (h, k) and slope 'm' will be,
y - k = m(x - h)
If this line passes through a point (-3, 1) and has a slope 2/3 32 .
Therefore, equation of the line will be,
y-1=2/3(x+3)y−1=32(x+3)
y=2/3+2+1y=32x+2+1
y=2/3 x+3y=32x+3
Therefore, equation of the line will be,
y=2/3x+3y=32x+3
P.S (2/3- fraction)
. The table below shows the cost of making a long distance call based on the length of the call. Long Distance Rates Time (minutes) Cost 5 $0.55 6 $0.62 7 $0.69 8 $0.76 9 $0.83 10 $0.90 Refer to the above table of long distance rates. Write an expression that can be used to find the cost of an n-minute long distance call, where n is at least 5 minutes.
Answers
An expression that can be used to find the cost of an n-minute long distance call, where n is at least 5 minutes is (0.55 + (n - 5) x 0.07) dollars.
Given:
Long Distance Rates Time (minutes) Cost5 $0.556 $0.627 $0.698 $0.769 $0.8310 $0.90We need to find an expression that can be used to find the cost of an n-minute long-distance call, where n is at least 5 minutes.
The cost of making a long-distance call is given for 5 minutes, 6 minutes, 7 minutes, 8 minutes, 9 minutes, and 10 minutes.
We can observe from the above table that for every increase of 1 minute, the cost increases by $0.07.
We can conclude that the cost of n minutes long-distance call is given by: (0.55 + (n - 5) x 0.07) dollars when n is at least 5 minutes.
Therefore, the required expression is: (0.55 + (n - 5) x 0.07) dollars when n is at least 5 minutes. The above expression is based on the pattern in the table provided for long-distance call rates. We can use this expression for values of n greater than or equal to 5.
For more such questions on expression, click on:
https://brainly.com/question/723406
#SPJ8
8. The first three terms of a geometric sequence are ( x-6), 3x, and y. If the common ratio is 6, then the value of y is.
Answers
Answer:
The value of y is 216
(and the value of x is 12)
Step-by-step explanation:
The general formula for a geometric sequence is,
\(a_n = a_1(r)^{n-1}\)
Where n represents the nth term, a_1 is the first term and r is the common ratio,
we see that,
r = 6,
the first term is,
a_1 = (x-6)
the 2nd term is,
a_2 = 3x,
the 3rd term is,
a_3 = y, finding y,
first we find x, using the above given formula we have,
\(a_2 = a_1(6)^{2-1}\\3x = (x-6)(6^1)\\3x = 6x -36\\36 = 6x - 3x\\36 = 3x\\x=36/3\\x=12\)
x = 12,
Now, for y we can use the relation between a_3 and a_2,
\(a_3 = a_1(6)^{3-1}\\y = (x-6)(6)^2\\y = (12-6)(6^2)\\y = 6(6^2)\\y = 6^3\\y = 216\)
y = 216
What is 5 x 9 ÷ 3 - 3²?
Answers
Answer:
6
Step-by-step explanation:
Using PEMDAS, you would first do the exponent which is equal to 9. the following it you would do 5x9 which is 45 and divide it by 3 which gives you 15. finally you subtract the 9 from 15 and get 6.
Answer:
6
Step-by-step explanation:
5 x 9 ÷ 3 - 3²
5 x 9 ÷ 3 - 9
45 ÷ 3 - 9
15 - 9
6
use PEMDAS for the order of operations.
It is claimed that the average child has no time to go to school. For the child spends 8 hours per day,or one third of his/her time sleeping. Based on a 365 day year, that’s 121.67days sleeping. Also the child spends three hours per day eating. That’s a total of 45 days in the year spent eating. Also the child spends 90 days taking summer vacation. Also the child spends 21 days on Christmas and Easter holiday. Finally, the child has each Saturday and Sunday off. That’s a total of 104 days. In short, we (rounding to whole days accounted for 122+45+90+21+104=382 days of the year taken up by ordinary child inlike activities. This is already more than the 365 days that are known to comprise a year. We conclude that there is certainly no time for the child to attend school. What is wrong with this reasoning?
Answers
Answer:
See below.
Step-by-step explanation:
Sleeping:
8/24 * 365 = 121.76 days
Eating:
3/24 * 365 = 45.63 days
Total sleeping and eating: 167 days
Summer Vacation & Holidays:
90 + 21 = 111 days
Saturdays and Sundays: 52 + 52 = 104 days
Vacation + Holidays Saturdays + Sundays = 111 + 104 = 215 days
It may be true that all days of vacation, holiday, Saturdays, and Sundays combined are a total of 215 days, but these 215 days cannot be added to the 167 days above because these 215 days include time for sleeping and eating which was already included in the sleeping and eating times for the entire year. The mistake in the reasoning is counting twice the time of sleeping and eating on the 215 days in which there is no school.
Can a function have a y-value with more than one x value why or why not ?
Answers
can someone help me solve please.. thanks..

Answers
Answer:
see below
Step-by-step explanation:
f(0) means x=0
We use the f(x) when x<5
f(0) = 0+4 = 4
f(6) means x=6
We use the f(x) when 5≤x<7
f(6) =8
Find MN.
2x - 16
X-9

Answers
Answer:
3
Step-by-step explanation:
LN = 11
x - 9 + 2x - 16 = LN add like terms
3x - 25 = 11
3x = 36
x = 12
MN = x - 9 therefore MN = 3