In 2021, the population of a Texas city was 126,000. If the population is decreasing at an annual rate of 4.5%, what will the population be in 2029?
Answers
Answer:
81,000
Step-by-step explanation:
Related Questions
multiple choice qu 9-23 (static) part j [lo 9-6]j. in attributes sampling, what effect does a decrease in the tolerable deviation rate have on sample size?
Answers
The tolerable deviation rate decreases, it necessitates a larger sample size to maintain the desired level of confidence and accuracy in the Sampling size.
In attributes sampling, the tolerable deviation rate refers to the acceptable level of non-conforming items or errors in a population. It represents the maximum rate of deviation or non-conformance that is considered acceptable for a given attribute or characteristic being inspected.
When the tolerable deviation rate is decreased, it means that a lower level of deviation or non-conformance is deemed acceptable. This has an effect on the sample size required for the attributes sampling.
Generally, a decrease in the tolerable deviation rate will lead to an increase in the required sample size. The reason for this is that when the acceptable level of deviation is reduced, it becomes more stringent, and a larger sample is needed to ensure that the observed deviation rate is statistically representative of the population.
By increasing the sample size, there is a higher likelihood of capturing a sufficient number of defective or non-conforming items to make reliable conclusions about the population's quality level. This helps to reduce the risk of accepting a batch or population that actually has a higher defect rate than what is considered tolerable.
the tolerable deviation rate decreases, it necessitates a larger sample size to maintain the desired level of confidence and accuracy in the sampling results. The increased sample size allows for a more precise estimation of the population's quality level, providing greater assurance in decision-making regarding acceptance or rejection of the population based on the observed deviation rate.
To know more about Sampling size.
https://brainly.com/question/30647570
#SPJ11
Someone please help me with these 4

Answers
Answer:
1) Alternating Interior angels supplementary
2) Corresponding angels congruent
3) Alternating Interior Angles congruent 93º
4) Alternating Interior Angles congruent 96º if it says 96º on the paper it's blurry
Step-by-step explanation:
Simplify each radical expression, if possible 3v/7-5^4v/7
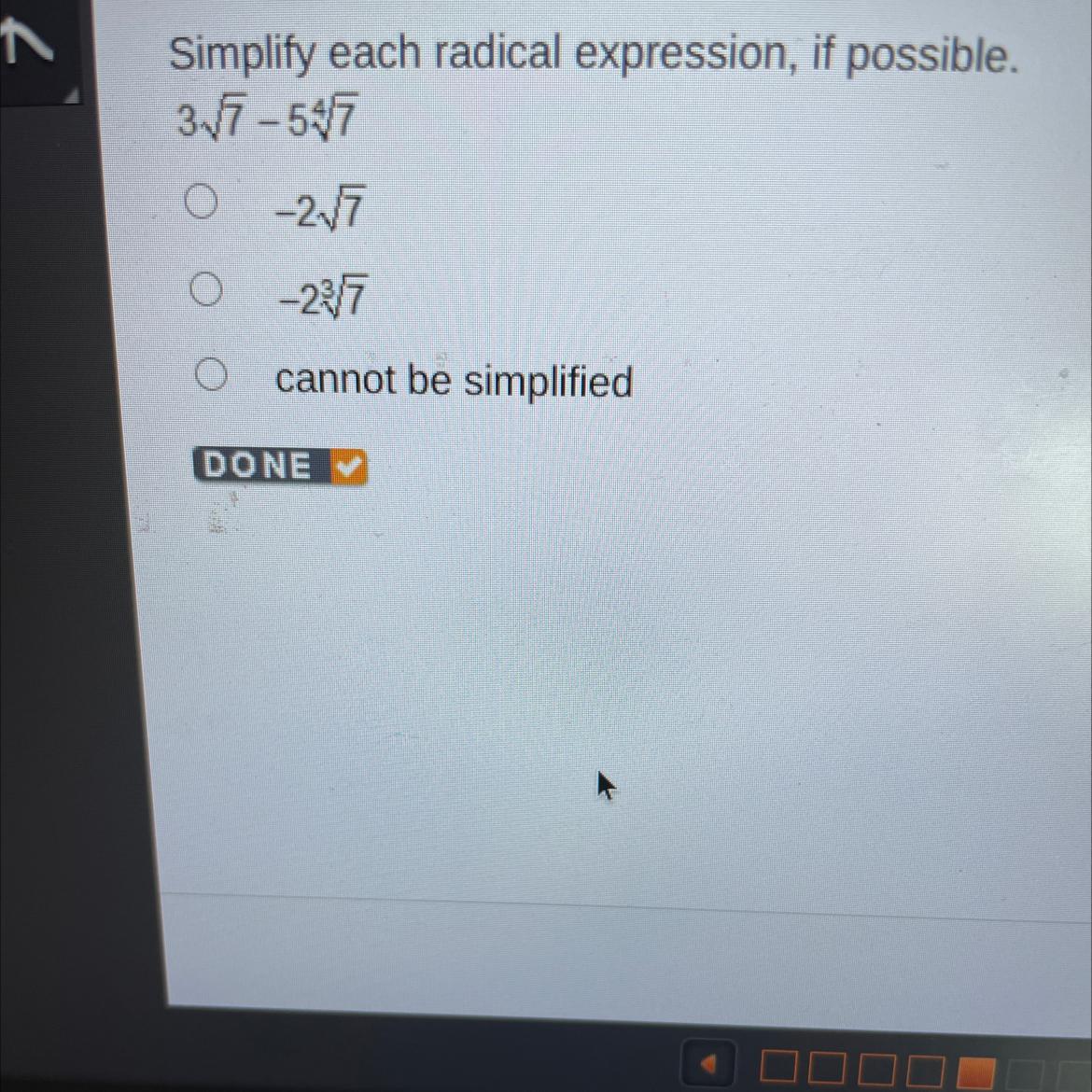
Answers
Answer:
cannot be simplified
Step -by-step explanation:
\(3\sqrt{7} - 5\sqrt[4]{7} \\\)
The indexes are not the same so the radicals cannot be combined.
cannot be simplified
assume that a bond sells at $92.10 and its modified duration is 4.03. compute dollar duration. answer with two decimal digits accuracy and the correct sign. example:-800.00
Answers
The dollar duration of the given bond is $3.71
Dollar duration:
Dollar duration means a linear approximation of how a bond's value will change in response to changes in interest rates.
Given,
Here we have to assume that a bond sells at $92.10 and its modified duration is 4.03.
And we need to compute dollar duration. answer with two decimal digits accuracy and the correct sign.
As per the formula of dollar duration, the values of
bond price = $92.10
duration = 4.03
interest rate = 0.01
So, the dollar duration is calculated as follows,
=> dollar duration = 0.01 x 92.10 x 4.03
=> dollar duration = 3.71
To know more about Dollar duration here.
https://brainly.com/question/14219464
#SPJ4
Which property should Remus use to solve the equation below? 7 q = 49 division property of equality addition property of equality subtraction property of equality identity property of equality.
Answers
Answer:
Division Property
Step-by-step explanation:
He needs to divide both sides by 7 to find the value of q
The division property of equality should Remus used to solve the given equation and this can be determined by using the given data.
Given :
Equation is \(7q = 49\).
The following steps can be used in order to determine the property that Remus use to solve the given equation:
Step 1 - Write the given equation.
\(7q = 49\)
Step 2 - The arithmetic operations can be used in order to evaluate the given equation.
Step 3 - Using the division property of equality the value of 'q' can be determined.
\(q = \dfrac{49}{7}\)
\(q = 7\)
Therefore, the correct option is A).
For more information, refer to the link given below:
https://brainly.com/question/11897796
Is 2 − –46 positive or negative?
Answers
Answer:
Negative
Step-by-step explanation:
Positive + Positive= Positive
Negative +Negative= Positive
Positive +Negative Or Negative + Positive= Negative
How do you graph sin and cosine?
Answers
Graphing sine and cosine functions is a key concept in trigonometry. To graph sine and cosine, you need to know the basic characteristics of these functions and how they relate to the unit circle.
The sine function, represented by y = sin(x), has a range of -1 to 1 and a period of 2π. The cosine function, represented by y = cos(x), also has a range of -1 to 1 and a period of 2π. The sine and cosine functions are closely related to the unit circle, which is a circle with a radius of 1 centered at the origin of a coordinate plane.
To graph sine, you can start by identifying the key points of the function: the maximum, minimum and zeroes. You can also use the period, which is 2π, to find the x-coordinates of these key points.
Similarly, to graph cosine, you need to identify the key points of the function which are the maximum, minimum, and zeroes. You can use the period, which is 2π, to find the x-coordinates of these key points.
It is important to note that sine and cosine graphs are periodic and they repeat after certain interval of 2π.
In summary, graphing sine and cosine is a matter of understanding the characteristics and properties of these functions, and using them to identify the key points of the functions which can be plotted on the coordinate plane.
to know more about graph refer here
brainly.com/question/17267403#
#SPJ11
find the equation of the hyperbola with vertices (2,5) and (2,−3) and foci (2,10) and (2,−8).
Answers
The equation of the hyperbola is (y - 1)^2 / 16 - (x - 2)^2 / 65 = 1
To find the equation of the hyperbola, we need to determine its center, vertices, and foci.
Given:
Vertices: (2, 5) and (2, -3)
Foci: (2, 10) and (2, -8)
The center of the hyperbola is the midpoint between the vertices, which can be found by averaging their x-coordinates and y-coordinates:
Center: (2, (5 + (-3))/2) = (2, 1)
The distance between the center and the vertices is denoted by "a". In this case, the distance is the absolute value of the difference between the y-coordinates of the center and one of the vertices:
a = |1 - 5| = 4
The distance between the center and the foci is denoted by "c". In this case, the distance is the absolute value of the difference between the y-coordinates of the center and one of the foci:
c = |1 - 10| = 9
The relationship between "a", "b", and "c" in a hyperbola is given by the equation:
c^2 = a^2 + b^2
Solving for "b^2", we have:
b^2 = c^2 - a^2
= 9^2 - 4^2
= 81 - 16
= 65
Now we have all the necessary information to write the equation of the hyperbola in standard form:
For a horizontal hyperbola:
(x - h)^2 / a^2 - (y - k)^2 / b^2 = 1
For a vertical hyperbola:
(y - k)^2 / a^2 - (x - h)^2 / b^2 = 1
Since the given foci have the same x-coordinate, the hyperbola is vertical. Plugging in the values:
(y - 1)^2 / 4^2 - (x - 2)^2 / √65 = 1
Simplifying, we have:
(y - 1)^2 / 16 - (x - 2)^2 / 65 = 1
Therefore, the equation of the hyperbola is:
(y - 1)^2 / 16 - (x - 2)^2 / 65 = 1
To learn more about hyperbola go to:
https://brainly.com/question/15697124?referrer=searchResults
#SPJ11
How many liters of a 35 percent salt solution must be mixed with 20 liters of a 70 percent salt solution to obtain a solution that is 45 percent salt
Answers
86 liters of 35% salt solution should be added to 20 liters of an 70% salt solution so that the resulting solution contains 45% salt solution .
For given question,
Let x be the quantity ( in liters ) of 35 percent salt solution added to 20 liters of an 70 percent salt solution so that the resulting solution contains 45 percent salt,
Thus,
Quantity of salt solution in 20 liters + Quantity of salt solution in x
= Quantity of salt solution in resultant mixture.
⇒ 70% of 20 + 35% of x = 45% of (20 + x )
⇒ 14 + (0.35x) = 0.45 × ( 12 + x )
⇒ 14 + 0.35x = 5.4 + 0.45x
⇒ 14 - 5.4 = 0.45x - 0.35x
⇒ 8.6 = 0.10x
⇒ x = 86 liters
Therefore, 86 liters of 35% salt solution should be added to 20 liters of an 70% salt solution so that the resulting solution contains 45% salt solution .
Learn more about the resulting solution here:
brainly.com/question/12051765
#SPJ4
Jermaine has to work with the formula, A = L x W , to find the length of his backyard. He needs to rearrange the formula to solve for "L" the length. what would the new formula look like
Answers
l = a x w
Hes trying to find lenth so the equal we be getting a and w's attention
12(Multiple Choice Worth 5 points)
(H2.03 MC)
Which of the following is NOT a key feature of the function h(x)?
(x - 5)²
-log₁ x +6
O The domain of h(x) is [0.).
O The x-intercept of h(x) is (5, 0)
h(x) =
0≤x≤4
X>4
O The y-intercept of h(x) is (0, 25).
O The end behavior of h(x) is as x→∞h(x)→∞

Answers
The feature NOT associated with the function h(x) is that the domain of h(x) is [0.).
The function h(x) is defined as (x - 5)² - log₁ x + 6.
Let's analyze each given option to determine which one is NOT a key feature of h(x).
Option 1 states that the domain of h(x) is [0, ∞).
However, the function h(x) contains a logarithm term, which is only defined for positive values of x.
Therefore, the domain of h(x) is actually (0, ∞).
This option is not a key feature of h(x).
Option 2 states that the x-intercept of h(x) is (5, 0).
To find the x-intercept, we set h(x) = 0 and solve for x. In this case, we have (x - 5)² - log₁ x + 6 = 0.
However, since the logarithm term is always positive, it can never equal zero.
Therefore, the function h(x) does not have an x-intercept at (5, 0).
This option is a key feature of h(x).
Option 3 states that the y-intercept of h(x) is (0, 25).
To find the y-intercept, we set x = 0 and evaluate h(x). Plugging in x = 0, we get (0 - 5)² - log₁ 0 + 6.
However, the logarithm of 0 is undefined, so the y-intercept of h(x) is not (0, 25).
This option is not a key feature of h(x).
Option 4 states that the end behavior of h(x) is as x approaches infinity, h(x) approaches infinity.
This is true because as x becomes larger, the square term (x - 5)² dominates, causing h(x) to approach positive infinity.
This option is a key feature of h(x).
In conclusion, the key feature of h(x) that is NOT mentioned in the given options is that the domain of h(x) is (0, ∞).
Therefore, the correct answer is:
O The domain of h(x) is (0, ∞).
For similar question on domain.
https://brainly.com/question/2264373
#SPJ8
5) The length of a rectangle is 5 more than 10 times the width. The perimeter is 230cm find the length and width of the rectangle. (I need help please!)
Answers
Answer:
length =105 width =10
Step-by-step explanation:
L=10*W+5
P=230
P=2(L+W)
230=2(10W+5+W)
SOLVE FOR W
W=10
L=10*W+5
=10*10+5
L=105
PLZ HELP!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
Answer:
b
Step-by-step explanation:
WILL GIVE BRAINLIEST IF CORRECT!!!

Answers
Answer:
<ACB = 63 degrees
Step-by-step explanation:
FG = HG thus <H nd <F are congruent
180 - 54 = 126/2 = 63 degrees
<HFG = <ACB (alternate exterior angles)
I will give brainliest if you answer please

Answers
Answer:
KN = 11
Step-by-step explanation:
In right triangle LNM, by Pythagoras theorem:
\(LN=\sqrt{LM^2 -MN^2} \\ \\ \implies \: LN=\sqrt{ {(100)}^{2} -(80)^2} \\ \\ \implies \: LN=\sqrt{ 10000 -6400} \\ \\ \implies \: LN=\sqrt{ 3600} \\ \\ \implies \: LN=60\)
In right triangle LNK, by Pythagoras theorem:
\(KN = \sqrt{LK^2-LN^2}\)
\(\implies KN = \sqrt{(61)^2-(60)^2}\)
\(\implies KN = \sqrt{3721-3600}\)
\(\implies KN = \sqrt{121}\)
\(\implies\huge{\orange{ KN =11}}\)
Answer:
11\( \: \)
Step-by-step explanation:
Before, Finding the length of KN, we must have to find the length of LN. So
\( \: \)
Here, LNM is a right angled triangle where measure of two sides are given and we are to find the measure of the third side LN(Perpendicular).
\( \: \)
We'll find the measure of third side with the help of the Pythagorean theorem.
\( \\ {\longrightarrow \pmb{\sf {\qquad (Base) {}^{2} + (Perpendicular {)}^{2} = (Hypotenuse {)}^{2} }}} \\ \\\)
Here,
The base (NM) is 80The perpendicular is LNThe hypotenuse (LM) is 100.\( \: \)
So, substituting the values in the above formula we get :
\(\\ {\longrightarrow \pmb{\sf {\qquad (NM) {}^{2} + (LN {)}^{2} = ( LM{)}^{2} }}} \\ \\\)
\( {\longrightarrow \pmb{\sf {\qquad (80) {}^{2} + (LN {)}^{2} = ( 100{)}^{2} }}} \\ \\\)
\( {\longrightarrow \pmb{\sf {\qquad (LN {)}^{2} = ( 100{)}^{2} - (80) {}^{2}}}} \\ \\\)
\( {\longrightarrow \pmb{\sf {\qquad (LN {)}^{2} = 10000 - 6400}}} \\ \\\)
\( {\longrightarrow \pmb{\sf {\qquad (LN {)}^{2} = 3600}}} \\ \\\)
\( {\longrightarrow \pmb{\sf {\qquad LN = \sqrt{3600} }}} \\ \\\)
\({\longrightarrow \pmb{\sf {\qquad LN = \frak{60}}}} \\ \\\)
Therefore,
The length of LN is 60.\( \\ \)
As, we found the length of LN, now we can find the length of KN.
Where,
The base is KNThe perpendicular (LN) is 60.The hypotenuse (LK) is 61.So, in the right angled triangle LKN, by Pythagorean theorem we get,
\(\\ {\longrightarrow \pmb{\sf {\qquad (KN) {}^{2} + (LN {)}^{2} = ( LK{)}^{2} }}} \\ \\\)
\({\longrightarrow \pmb{\sf {\qquad (KN) {}^{2} + {60}^{2} = ( 61{)}^{2} }}} \\ \\\)
\({\longrightarrow \pmb{\sf {\qquad (KN) {}^{2} = ( 61{)}^{2} - {(60)}^{2}}}} \\ \\\)
\({\longrightarrow \pmb{\sf {\qquad (KN) {}^{2} =3721 - 3600}}} \\ \\\)
\({\longrightarrow \pmb{\sf {\qquad (KN) {}^{2} = 121}}} \\ \\\)
\({\longrightarrow \pmb{\sf {\qquad KN = \sqrt{121} }}} \\ \\\)
\({\longrightarrow \pmb{\sf {\qquad KN = \frak{11} }}} \\ \\\)
Therefore,
The length of KN is 11.Last week , the rate of vegetable was RS 50 per kg and this week it is increased to RS 55 per kg , find the percentage of increased in the price.
Answers
Given,
Rate of vegetables last week = 50 per kg
Rate of vegetables this week= 55 per kg
Percentage increase in price = \(\frac{Rate of \: veg \: this \:week-Rate \: of \: veg \: last \: week}{Rate \: of \: veg \: last \:week} \times 100\)
\( = \frac{55 - 50}{50} \times 100\)
\( = \frac{5}{50} \times 100\)
\( = 5 \times 2\)
\( = 10\%\)
\({{\bold{ \underline{ \underline{ \overline{ \overline{ \pink{The \: percentage \: of \: increased \: in \: the \: price \: is \: 10\%}}}}}}}}\)
Do your thing genius's.

Answers
Answer:
1. True.
2. True.
3. True.
4. False.
5. True.
you guys help me rn!!
which two lines are parallell

Answers
Answer:
line k is parallel to line m
Step-by-step explanation:
120 + 60 = 180
but these are co interior angles for lines k and m.
hence the lines k and m are parallel to each other
7. In the diagram below of parallelogram ABCD, AFGB, CF bisects angle DCB, DG bisects angle ADC, and CF and
DG intersect at E.
If m/B= 75°, then the measure of angle EFA is
Answers
The value of the angle m∠EFA is: 127.5°
How to find the angle of the parallelogram?A parallelogram is defined as a quadrilateral that has its opposite sides parallel and equal to each other. It has its interior opposite angles equal. Also, the angles on the same side of the transversal sum up to 180 degrees or are supplementary to each other.
Since the figure is a parallelogram, it means that:
DC║AB
Thus:
m∠B = 75°
m∠DCB = 180° - 75°
m∠DCB = 105°
CF bisects ∠DCB
Thus:
m∠DCF = m∠FCB = ¹/₂ * 105° = 52.5°
Thus:
m∠EFA = 180° - 52.5°
m∠EFA = 127.5°
Read more about Angle of parallelogram at: https://brainly.com/question/24056495
#SPJ1
what is the shortest possible distance between the houses

Answers
Answer:
A.) 8.5 miles
Step-by-step explanation:
I think its a because it says "THE SHORTEST possible" distance between the houses. So A.) 8.5 miles is the correct answer because A.)8 .5 miles is the shortest answer in the list of answers.
Hope this helped.
The shortest distance between the two houses is 13 miles.
What is Pythagoras's theorem?In a right-angled triangle, the sum of the squares of the smaller two sides of a right-angle triangle is equal to the square of the largest side.
By observing the diagram we conclude that the shortest distance is the hypotenuse of the right-angled triangle that will form.
Given, The base is 12 miles and the height is 5 miles.
Therefore by Pythagoras' theorem,
Hypotenuse = √(5² + 12²).
Hypotenuse = √(25 + 144).
Hypotenuse = √(169).
Hypotenuse = 13 miles.
So, The shortest distance between the houses is 13 miles.
learn more about Pythagoras' theorem here :
https://brainly.com/question/343682
#SPJ2
Simplify radicals
Square root of 300
Answers
Answer:
10sqrt3
Step-by-step explanation:
sqrt300
= sqrt(100*3)
=10sqrt3
the rate of college enrollment immediately after high school completion was 67
Answers
The statement " Rate of college enrollment immediately after completing high school was 67% by 1997" is an example of (a) Descriptive Statistics.
The Descriptive statistics involves the use of measures, such as averages, proportions, and frequencies, to summarize and describe the main features of a set of data.
In this statement, the rate of 67% is a summary statistic that describes the proportion of high school graduates who enrolled in college immediately after completing high school in 1997.
Whereas; the inferential statistics involves making inferences or predictions about a population based on a sample of data.
The statement provides a summary statistic for the rate of college enrollment for a specific year, 1997, but it does not provide any inferences or predictions about the rate of college enrollment for other years or other populations , so it denoted a Descriptive Statistics .
The given question is incomplete , the complete question is
What type of Statistics does the statement "the rate of college enrollment immediately after high school completion was 67" represents ?
(a) Descriptive
(b) Inferential
Learn more about Descriptive Statistics here
https://brainly.com/question/29487303
#SPJ4
A recipe for making chocolate chip cookies calls for 2 1/2 cups of sugar for a dozen cookies (12). If you want to make 30 cookies, choose a proportion that would work to tell you how many cups of sugar you should use.
A: x/12 = 2.5/30
B: 2.5/12 = x/30
C: 2.5/30 = 12/x
D: 12/2.5 = x/30
Answers
Answer:
B: 2.5/12 = x/30
Step-by-step explanation:
We can use ratios to help solve. We need to keep the units in the same order.
2.5 cups sugar x cups sugar
-------------------- = ------------------
12 cookies 30 cookies
The small round holes you often see in sea shells were drilled by other sea creatures, who ate the former dwellers of the shells. Whelks often drill into mussels, but this behavior appears to be more or less common in different locations. Researchers collected whelk eggs from the coast of Oregon, raised the whelks in the laboratory, and then put each whelk in a container with some delicious mussels. Only 9 of 98 whelks drilled into a mussel. Check to see if the conditions for calculating a confidence interval for p are met, where p = the proportion of all Oregon whelks that will spontaneously drill into mussels. A. Random? Collected 98 whelk eggs (not sure if random) √ Large Counts? 98(9/98) = 9 ≥ 10 and 98(89/98) = 89 ≥10 √ B. Fails Random and Large Counts C. Fails Large Counts D. Not Random
Answers
The conditions for calculating a confidence interval for the proportion (p) of all Oregon whelks that will spontaneously drill into mussels are met.
To determine if the conditions for calculating a confidence interval for p are met, two criteria need to be considered: random sampling and large counts.
A. Random Sampling: The information provided does not specify if the whelk eggs were collected randomly. Therefore, this condition is not confirmed.
B. Large Counts: The condition of large counts is met if both np and n(1-p) are greater than or equal to 10, where n is the sample size and p is the proportion of interest. In this case, the sample size is 98, and the number of whelks that drilled into mussels is 9. Thus, np = 98 * (9/98) = 9, and n(1-p) = 98 * (89/98) = 89. Since both values are greater than or equal to 10, the condition of large counts is satisfied.
Based on the analysis, the condition of large counts is met, but the condition of random sampling is not confirmed. Therefore, the correct answer would be B. Fails Random and Large Counts.
Learn more about random sampling here: brainly.com/question/30759604
#SPJ11
at what rate is the base of the triangle changing when the altitude is 20 cm and the area is 120 cm2?
Answers
The rate at which the base of the triangle is changing when the altitude is 20 cm and the area is 120 cm^2 is 0 cm/s.
To solve this problem, we need to use the formula for the area of a triangle, which is:
A = (1/2)bh
Where A is the area, b is the base, and h is the altitude.
We know that the area is 120 cm^2 and the altitude is 20 cm. So we can plug in these values and solve for the base:
120 = (1/2)b(20)
240 = 20b
b = 12 cm
Now we need to differentiate both sides of the equation with respect to time (t):
dA/dt = (1/2)(db/dt)h
We are given the value of dh/dt (which represents the rate at which the altitude is changing) is 3 cm/s. We need to find db/dt (which represents the rate at which the base is changing).
Plugging in the values we know, we get:
dA/dt = (1/2)(db/dt)(20)
Solving for db/dt, we get:
db/dt = (2dA/dt)/h
Plugging in the values we know, we get:
db/dt = (2)(0)/20
db/dt = 0 cm/s
Since the area is constant (120 cm²) and the altitude is constant (20 cm), the base of the triangle is not changing. Therefore, the rate at which the base is changing is: 0 cm/s
Learn about application of derivatives here: brainly.com/question/25120629
#SPJ11
Diagonalize the following matrix. The real eigenvalues are given to the right of the matrix. ⎣
⎡
3
3
−3
18
0
9
18
−9
18
⎦
⎤
;λ=3,9 Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. For P=,D= ⎣
⎡
3
0
0
0
3
0
0
0
9
⎦
⎤
B. For P= P=,D= ⎣
⎡
3
0
0
0
9
0
0
0
9
⎦
⎤
C. The matrix cannot be diagonalized
Answers
The matrix can be diagonalized, and the correct choice is B. For P= ⎡⎣3−11011⎤⎦, D= ⎡⎣393000⎤⎦.
To diagonalize a matrix, we need to find its eigenvectors and use them to construct a matrix P, where the columns of P are the eigenvectors. The diagonal matrix D is formed by placing the eigenvalues on the diagonal.
First, we find the eigenvalues λ by solving the characteristic equation det(A - λI) = 0, where A is the given matrix and I is the identity matrix. By calculating the determinant, we have (33 - λ)(9 - λ) - (-3)(18) = 0, which simplifies to λ^2 - 42λ + 315 = 0. Solving this quadratic equation gives λ = 3 and λ = 9.
Next, we find the corresponding eigenvectors. For λ = 3, we solve the equation (A - 3I)v = 0, where v is the eigenvector. This leads to the eigenvector v = ⎡⎣3−110⎤⎦. For λ = 9, we solve (A - 9I)v = 0, which gives v = ⎡⎣111⎤⎦.
We construct matrix P by using the eigenvectors as columns: P = ⎡⎣3−11011⎤⎦. The diagonal matrix D is formed by placing the eigenvalues on the diagonal: D = ⎡⎣393000⎤⎦.
Therefore, the correct choice is B. For P= ⎡⎣3−11011⎤⎦, D= ⎡⎣393000⎤⎦.
Learn more about diagonalization of matrices here: brainly.com/question/32422878
#SPJ11
A marksman at rest fires a 4.00 -kg gun that expels a bullet of mass 0.014 kg with a velocity of 181 m/s. the marksman’s mass is 81 kg. what is the marksman’s velocity after firing the gun?
Answers
The marksman's velocity after firing the gun is about -0.63 m/s (in the opposite direction of the bullet's velocity), as calculated using the conservation of momentum principle.
The conservation of momentum principle can be used to resolve this issue. The initial momentum of the system (marksman plus gun) is zero, and the final momentum is also zero because the bullet and the marksman have equal and opposite momenta. Therefore, we can write:
initial momentum = final momentum
\(0 = (M + m) * V + m * v\)
where M is the mass of the gun, m is the mass of the bullet, V is the velocity of the gun after firing, and v is the velocity of the bullet after firing (which is 181 m/s in this case).
Solving for V, we get:
\(V = - m * v / (M + m)\)
= \(\frac{- 0.014 kg * 181 m/s}{(4.00 kg + 0.014 kg)}\) ≈ -0.63 m/s
Therefore, the marksman's velocity after firing the gun is about -0.63 m/s (in the opposite direction of the bullet's velocity).
Learn more about velocity here:
https://brainly.com/question/17127206
#SPJ4
Estimate the product first. solve by using the standard algorithm. use your estimate to check the reasonableness of the product
Answers
Let the estimated product of 512 and 46 using the standard algorithm is
5 1 2
× 4 6
3 0 7 2
+ 2 0 4 8
2 3 5 5 2
let,
512 and 46
Using the standard algorithm, we must find the product.
What is the typical algorithm for multiplying numbers?
Example:
12 x 13 = 156
12 x 1 = 12
12 x 3 = 36
Now,
1 2
× 1 3
3 6
+ 1 2
1 5 6
We have,
512 x 46 = 23552
The Standard algorithm is:
512 x 4 = 2048
512 x 6 = 3072
5 1 2
× 4 6
3 0 7 2
+ 2 0 4 8
2 3 5 5 2
The result of multiplying 512 by 46 using the conventional procedure is 23552.
Learn more about how to divide using a standard algorithm here:
https://brainly.com/question/8436704
#SPJ4
kyle works at a local music store. the store receives a shipment of new cds in a box. in the shipment, there are 10 country cds, 5 rock cds, 12 hip hop cds, and 3 jazz cds. what is the probability that the first cd that kyle pulls from the box will not be hip hop?
Answers
The probability that the first CD that Kyle pulls from the box will not be hip hop is 11/30, or 0.367.
There are 10 country CDs, 5 rock CDs, 12 hip hop CDs, and 3 jazz CDs in the box.
This means there are a total of 30 CDs in the box.
The probability that the first CD that Kyle pulls from the box will not be hip hop is the number of CDs that are not hip hop (10 + 5 + 3) divided by the total number of CDs (30).Therefore, the probability that the first CD that Kyle pulls from the box will not be hip hop is 11/30, or 0.367.The probability that the second CD that Kyle pulls from the box will not be hip hop is also 11/30, or 0.367. This is because the probability does not change regardless of which CD is chosen first. Similarly, the probability that the third, fourth, fifth, etc. CDs pulled from the box will not be hip hop is also 11/30, or 0.367.
Learn more about probability here
https://brainly.com/question/11234923
#SPJ4
image of infoYo
FILL IN THE BLANK. For the statement Q R, identify the Inverse, Converse, Contrapositive and original statement. ______R→Q _____~R→~Q _____Q → R _____~Q→~R
Answers
For the statement Q R, the Inverse is ~R→~Q, the Converse is R→Q, the Contrapositive is ~Q→~R, and the original statement is Q→R. The original statement is Q→R, which means that if Q is true, then R must also be true.
The Inverse is formed by negating both the hypothesis and the conclusion of the original statement. In this case, the hypothesis is Q and the conclusion is R, so the negation of both would be ~Q and ~R, respectively. The resulting statement is ~R→~Q. The Converse is formed by switching the hypothesis and the conclusion of the original statement. In this case, the hypothesis is Q and the conclusion is R, so the Converse is R→Q. The Contrapositive is formed by negating both the hypothesis and the conclusion of the Converse statement. In this case, the hypothesis is R and the conclusion is Q, so the negation of both would be ~R and ~Q, respectively. The resulting statement is ~Q→~R.
Learn more about Contrapositive here:
https://brainly.com/question/12151500
#SPJ11