In quadrilateral QRST, m∠Q > is 68°, m∠R is (3x + 40)°, and m∠T is (5x − 52)°. What are the measures of ∠R, ∠S, and ∠T? Write the numerical values in that order with the measures separated by commas.
Answers
A quadrilateral is a polygon with 4 number of sides and 4 vertices. The measure of ∠R, ∠S, and ∠T is 112°, 112°, and 68°, respectively.
What is a quadrilateral?A quadrilateral is a polygon with 4 number of sides and 4 vertices. A few examples of a quadrilateral are square, rectangle, rhombus, parallelogram, etc.
Since the given quadrilateral is a cyclic quadrilateral, therefore, the sum of the opposite angles of the quadrilateral will be 180°. Therefore, the sum of the ∠R and ∠T can be written as,
∠R + ∠T = 180°
(3x + 40) + (5x − 52) = 180
3x + 40 + 5x - 52 = 180
8x - 12 = 180
8x = 168
x = 24
Now, the measure of angle ∠R and ∠T can be written as,
∠T = 5x − 52 = 5(24) − 52 = 68°
∠R = 3x + 40 = 3(24) + 40 = 112°
Also, the sum of ∠Q and ∠S is 180°. Therefore,
∠Q + ∠S = 180°
68° + ∠S = 180°
∠S = 112°
Hence, the measure of ∠R, ∠S, and ∠T is 112°, 112°, and 68°, respectively.
Learn more about Quadrilateral:
https://brainly.com/question/13805601
#SPJ1
Related Questions
What percent of 75 is 80?
Answers
Answer:
\(106.67\text{\%}\)Explanation:
We want to find what percent of 75 is 80;
to get that we will divide 80 by 75 and multiply by 100%.
\(\begin{gathered} P=\frac{80}{75}\times100\text{\%} \\ P=1.0667\times100\text{\%} \\ P=106.67\text{\%} \end{gathered}\)Therefore, 80 is 106.67% of 75.
\(106.67\text{\%}\)Help plzzzzzzzzzbsjensbsbabbasb

Answers
Solve the following system of linear equations using the Gauss-Jordan elimination method. Be sure to show all of your steps and use the proper notation for the row operations that we defined in class. -3z-9y=-15 2x-8y=-4
Answers
The solution of the given system of equations isz = 0, y = -3, x = -11/2.
Hence, the complete solution of the given system of equations is (-11/2, -3, 0).
Given System of linear equations are
-3z - 9y
= -15 ----(1) 2x - 8y
= -4 ----(2)
Using Gauss-Jordan elimination method, the augmented matrix of the system of equations is:
[-3 -9 -15 | 0] [2 -8 -4 | 0]
Step 1: To obtain a 1 in the first row and the first column, multiply row 1 by -1/3 to obtain[-1 3 5 | 0] [2 -8 -4 | 0]
Step 2: Add 2 times row 1 to row 2 to obtain[-1 3 5 | 0] [0 -2 6 | 0]
Step 3: Divide row 2 by -2 to obtain[1 -3/2 -5/2 | 0] [0 1 -3 | 0]
Step 4: Add 3/2 times row 2 to row 1 to obtain[1 0 -11/2 | 0] [0 1 -3 | 0].
The solution of the given system of equations isz
= 0, y
= -3, x
= -11/2.
Hence, the complete solution of the given system of equations is (-11/2, -3, 0).
To know more about equations visit:
https://brainly.com/question/14686792
#SPJ11
If you go down 2 miles and the go 3 miles to the right what is the full number to complete the triangle
Answers
Answer:
4 miles
Step-by-step explanation:
go down 2 miles and then going 3 miles to the right we will make the side and base of the triangle,
the missing one would be the biggest side, i.e. the hypotenuse which we will find by Pythagoras theorem,
h = √a² + b²
= √4 + 9
= √13
= 3.6 = 4
thus 4 is the full number to complete the triangle.
Compare the pair of numbers. Use <, =, or >. 3/4 (_) 33/40
asap plss
Answers
Answer:
\(\frac{3}{4} < \frac{33}{40}\)
Explanation:
\(\frac{3}{4}\) (< = >) \(\frac{33}{40}\)
To figure this out, you want both fractions to have the same denominator. So, you would find the GCF (Greatest Common Factor).
The GCF for 4 and 40 would be 40 because 4 * 10 = 40 and 40 * 1 = 40.
To make the whole fraction have the denominator 40, you have to multiply the numerator and the denominator by 10.
\(\frac{3}{4} = \frac{30}{40}\)
So,
\(\frac{30}{40} < \frac{33}{40}\)
or
\(\frac{3}{4} < \frac{33}{40}\)
left side is off a polygon have length 5, 7, 8, 11 and 19 cm of a similar polygons is 75 cm find the lengths of the sides of large polygon
Answers
Answer:
df
Step-by-step explanation:
df
Answer:
7.5 , 10.5 , 12 , 16.5 , 28.5 are the sides of Larger polygon Step-by-step explanation: The sides of a polygon have lengths 5,7,8,11 and 19 cm Perimeter ...
Missing: left off
Step-by-step explanation:
thats it
whats 2+2 if you have 2 pencials A 4 B 4 C 4 D 8
Answers
Answer:
4.
Step-by-step explanation:
Answer:
4
Step-by-step explanation:
2+2=4
:)
PLS MARK ME THE BRAINLIEST I NEED 2 MORE TO GET TO EXPERT
Add.
(6x³ + 3x² − 2) + (x³ - 5x² − 3)
Express the answer in standard form. (Please and thank you)
Answers
Answer:
\(\\\sf7x^3 - 2x^2 - 5\)
Step-by-step explanation:
\(\\\sf(6x^3 + 3x^2 - 2) + (x^3 - 5x^2 - 3)\)
Remove parenthesis.
6x^3 + 3x^2 - 2 + x^3 - 5x^2 - 3
Rearrange:
6x^3 + x^3 + 3x^2 - 5x^2 - 2 - 3
Combine like terms to get:
7x^3 - 2x^2 - 5----------------------------------------
More on adding polynomials: https://brainly.com/question/30791478
Hope this helps! :)
Answer:
7x³ - 2x² - 5
Step-by-step explanation:
(6x³ + 3x² - 2) + (x³ - 5x² - 3)
Remove the round brackets.
= 6x³ + 3x² - 2 + x³ - 5x² - 3
Put like terms together.
= 6x³ + x³ + 3x² - 5x² - 2 - 3
Do the operations.
= 7x³ - 2x² - 5
____________
hope this helps!
For f(x) = -x-4 find the value of x for which f (x) = 1
Answers
Answer:
x = -5
Step-by-step explanation:
f(x) = -x-4
Let f(x) = 1
Find x
1 = -x-4
Add 4 to each side
1+4 = -x-4+4
5 = -x
Multiply each side by -1
-5 =x
x = -5
Answer:
x = -5
Step-by-step explanation:
Given that,
f ( x ) = - x - 4
If, f ( x ) = 1,
Let us find the value of x.
For that, replace f ( x ) with 1.
f ( x ) = - x - 4
1 = - x - 4
First, add x to both sides.
x + 1 = -4
Now, subtract 1 from both sides.
x = -4 - 1
x = -5
Solve for missing unit (Pythagorean theorem)
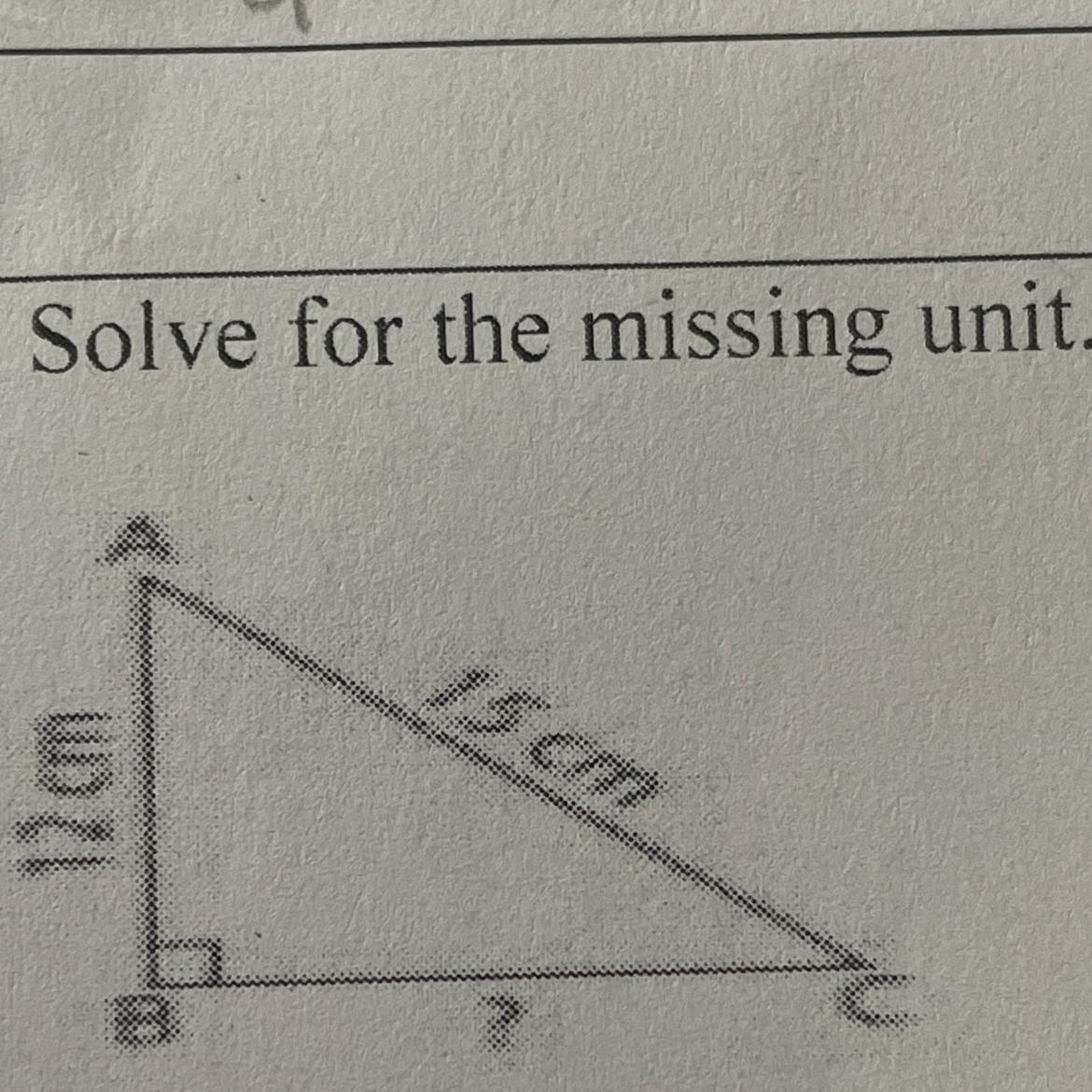
Answers
Answer:
Missing side is 9 cm
Step-by-step explanation:
a^2 + b^2 = c^3
(12)^2 + b^2 = (15)^2
144 + b^2 = 225
b^2 = 81
\(\sqrt{b^2}\) = \(\sqrt{81}\)
b = 9 cm
Find the distance on the number line between 14.3 and 4.1.
Answers
\(\\ \sf\longmapsto 14.3-4.1\)
\(\\ \sf\longmapsto \dfrac{143}{10}-\dfrac{41}{10}\)
\(\\ \sf\longmapsto \dfrac{143-41}{10}\)
\(\\ \sf\longmapsto \dfrac{102}{10}\)
\(\\ \sf\longmapsto 10.2\)
Hi~! can someone help me with this~?
It costs 3 bowls and a jug 13.70, the jug costs $4.10 more that the bowl, how much does the jug cost-?
Thank u~!
Answers
Answer:
$6.50
Step-by-step explanation:
Let the cost of a bowl and a jug be $b and $j respectively.
3b +j= 13.70 -----(1)
j= b +4.10 -----(2)
Substitute (2) into (1):
3b +b +4.10= 13.70
4b +4.10= 13.70 (simplify)
4b= 13.70 -4.10 (-4.10 on both sides)
4b= 9.60
b= 9.60 ÷4 (÷4 on both sides)
b= 2.40
Substitute b= 2.40 into (2):
j= 2.40 +4.10
j= 6.50
Thus, the jug costs $6.50.
I’m clueless! Can someone explain how to do this question step by step? Thanks! Extra points!! What is the average (arithmetic mean) of 4x + 5, 7x-6, and -8x+2?
Answers
Answer:
x+ 1/3 is the average
Step-by-step explanation:
To find the mean, add the terms together and then divide by the number of terms. There are 3 terms
(4x + 5+ 7x-6 + -8x+2)/3
Combine like terms
( 3x+1)/3
x+ 1/3 is the average
Simply the following expression

Answers
Answer:
the answer is A
Step-by-step explanation:
15 goes in both the 3 and 5 times table and 1×1=1
hi you can help me plis

Answers
Answer:
14
I hope it works for you
The number of weeds in my yard doubles every 3 weeks. If I initially have 80 weeds in my yard, what unit is most appropriate for the time at which the number of weeds is 120? (circle one) How do you know?
Week, Month, Weeds per week, Weeds per month
Answers
The unit that is most appropriate for the time at which the number of weeks is 120 is given as follows:
Week.
How to define an exponential function?The general format for an exponential function is given as follows:
\(y = a(b)^{\frac{x}{n}}\)
The parameters for the exponential function are defined as follows:
a is the initial value of the exponential function.b is the rate of change of the exponential function.n is the time that the exponential function for the rate of change.The number of weeds in my yard doubles every 3 weeks, and the initial number of weeks is of 80, hence the values of the parameters are given as follows:
a = 80, b = 2, n = 3.
As n = 3, we have that the unit of the output variable is of weeks, hence weeks is the appropriate measure in this problem.
More can be learned about an exponential function at https://brainly.com/question/25537936
#SPJ1
In the standard equation for a conic section Ax2 + Bxy + Cy2 + Dx + Ey + F = 0, if B2 − 4AC < 0, the conic section in question is a circle if A = C , B = 0.TrueFalse
Answers
For this problem we start from the equation given and susbtitute the conditions:
\(\begin{gathered} Ax^2+Bxy+Cy^2+Dx+Ey+F=0 \\ WenowusethatA=CandB=0andC>0(thiscomesfromB^2-4AC<0) \\ Cx^2+Cy^2+Dx+Ey+F=0 \\ \frac{C}{C}x^2+\frac{^{}D}{C}x+\frac{C}{C}y^2+\frac{E}{C}y=-\frac{F}{C} \end{gathered}\)Now we complete the perfect square trinomials:
\(\begin{gathered} x^2+\frac{D}{C}x+(\frac{D}{2C})^2+y^2+\frac{E}{C}y+(\frac{E}{2C})^2=-\frac{F}{C}+(\frac{D}{2C})^2+(\frac{E}{2C})^2 \\ (x+\frac{D}{2C})^2+(y+\frac{E}{2C})^2=-\frac{F}{C}+(\frac{D}{2C})^2+(\frac{E}{2C})^2=\text{ constant } \end{gathered}\)Now, we have arrived to the general form of an equation of a circle.
Answer: True.
Solve for xxx. Enter the solutions from least to greatest. 3x^2 - 9x - 12 = 03x
2
−9x−12=0
Answers
The solutions to the equation 3x^2 - 9x - 12 = 0 are x = 4 and x = -1.
To solve the quadratic equation 3x^2 - 9x - 12 = 0, we can use the quadratic formula:
x = (-b ± √(b^2 - 4ac)) / (2a),
where a, b, and c are the coefficients of the quadratic equation.
In this case, a = 3, b = -9, and c = -12. Substituting these values into the quadratic formula, we have:
x = (-(-9) ± √((-9)^2 - 4 * 3 * (-12))) / (2 * 3)
= (9 ± √(81 + 144)) / 6
= (9 ± √(225)) / 6
= (9 ± 15) / 6.
We have two possible solutions:
For the positive root:
x = (9 + 15) / 6
= 24 / 6
= 4.
For the negative root:
x = (9 - 15) / 6
= -6 / 6
= -1.
The solutions to the equation 3x^2 - 9x - 12 = 0 are x = 4 and x = -1.
for such more question on equation
https://brainly.com/question/17145398
#SPJ8
Fully simplifiy the following:
-2f × g × 7
Answers
Answer:
-14fg Your Welcome !!!
Step-by-step explanation:
A Number decreased by 2 times 5 is 60
Answers
Answer: The number is 14.
Step-by-step explanation:
14 minus 2 equals 12 and 12 times 5 equals 60.
Hope this helps :)
Have a great day!!
writing and graphing linear equations glass art
Answers
The graph of Linear Equation is always a straight line .
The rectangle shown has a perimeter of 54 cm and the given area. Its length is 3 more than 3 times its width. Write and solve a system of equations to find the dimensions of the rectangle.
The length of the rectangle is what cm ?
the width of the rectangle is
what cm.?
Answers
Answer:
Step-by-step explanation:
the perimeter P=2(L+W)=54
P=2L+2W=54 OR L+W=27
we know that L=3W+3
P=3W+W=27-3
4W=24
W=6 CM
L=21CM
SA police department used a radar gun to measure the speed of a sample of cars on the highway.
Assume that the distribution of speeds is approximately Normal with a mean of 71 mph and a
standard deviation of 8 mph.
Using this distribution what is the z-score of a 65-mph speed limit? *
Answers
Answer:
The z score of the 65-mph speed limit is -0.75
Step-by-step explanation:
The z score is given by the relation;
\(z = \frac{x- \mu}{\sigma}\)
Where:
Z = Normal (Standard) or z score
x = Observed speed score
μ = Mean, expected speed
σ = Standard deviation
Where we plug in the values for x = 65-mph, σ = 8 mph and μ = 71 mph, into the z-score equation, we get;
\(z = \frac{65-71}{8}= \frac{-6}{8} = -\frac{3}{4}\)
Hence the z score of the 65-mph speed limit =-3/4 or -0.75.
The sum of 9 times a number and 7 is 6
Answers
Given statement solution is :- The value of the number is -1/9.
Let's solve the problem step by step.
Let's assume the number we're looking for is represented by the variable "x".
The problem states that the sum of 9 times the number (9x) and 7 is equal to 6. We can write this as an equation:
9x + 7 = 6
To isolate the variable "x," we need to move the constant term (7) to the other side of the equation. We can do this by subtracting 7 from both sides:
9x + 7 - 7 = 6 - 7
This simplifies to:
9x = -1
Finally, to solve for "x," we divide both sides of the equation by 9:
9x/9 = -1/9
This simplifies to:
x = -1/9
So, the value of the number is -1/9.
For such more questions on value of the number
https://brainly.com/question/26150158
#SPJ8
A function g models a relationship in which the dependent variable is multiplied by 9
for every 2 units the independent variable increases. The value of the function at 0 is 2.
Which equation represents g?
Answers
The link represented by function g multiplies the dependent variable by 9 for every increase of 2 units in the independent variable. The equation that represents g is \(g(x)= 2 \times3^x\),and the function has a value of 2 at 0
Let x be the independent variable, and let g(x) be the dependent variable.
According to the problem, for every 2 units the independent variable increases, the dependent variable is multiplied by 9. This suggests an exponential relationship of the form:
\(g(x)= a \times b^x\)
where a is the initial value of the dependent variable (when x=0), and b is the growth factor (how much the dependent variable changes for every unit increase in x).
We are given that g(0) = 2, so we can plug in these values and solve for a:
\(g(0)= a \times b^0\)
a = 2
So now we have:
\(g(x)= 2 \times b^x\)
We still need to find the growth factor b. We are told that the dependent variable is multiplied by 9 for every 2 units the independent variable increases. In other words:
\(g(x+2) = 9 \times g(x)\)
Using our equation for g(x), we can substitute in and simplify:
\(2 \times b(x+2) = 9 \times 2\times b^x\)
Simplifying, we get:
\(b^2\) = 9
Taking the square root of both sides (we take the positive square root since b must be positive in order for g to be an increasing function), we get:
b = 3
So the final equation for g(x) is:
\(g(x) = 2 \times 3^x\)
For more such questions on variable
https://brainly.com/question/25223322
#SPJ4
The orbit of Halley’s comet, last seen in 1986 and due to return in 2061, is an ellipse with eccentricity 0.97 and one focus at the sun. The length of its major axis is 36.18 AU. [An astronomical unit (AU) is the mean distance between the earth and the sun, about 93 million miles.] Find a polar equation for the orbit of Halley’s comet. What is the maximum distance from the comet to the sun?
Answers
The polar equation for the orbit of Halley's comet is r = (18.09 AU)/(1 + 0.97*cos(theta)), where r represents the distance from the sun to the comet, and theta represents the angle between the major axis of the ellipse and the line connecting the sun and the comet.
The maximum distance from the comet to the sun occurs when theta is equal to 0 or 180 degrees, resulting in r = 36.18 AU.
Determine the polar equation?To derive the polar equation, we start with the general equation for an ellipse in polar coordinates: r = (a*(1 - e²))/(1 + e*cos(theta)), where a is the semi-major axis and e is the eccentricity.
Given that the major axis of Halley's comet is 36.18 AU and the eccentricity is 0.97, we can substitute these values into the equation to obtain r = (18.09 AU)/(1 + 0.97*cos(theta)).
This equation represents the polar equation for Halley's comet.
The maximum distance from the comet to the sun occurs when the cosine term is equal to -1, resulting in r = 36.18 AU.
To know more about distance, refer here:
https://brainly.com/question/15172156#
#SPJ4
A Bernoulli counting process has the following realization No-0, N-1, N2 = 1, N3 = 1, N4 = 2, Ns = 3, No = 3, N7 - 4, No = 4, N, - 5. a) What is the value of X6? b) What is the value of S;? c) What is the value of T2? d) If the success probability is p=0.2, What is P{N2=1, Ns=3, N7-4}?
Answers
Value of X6 = N6 - N5. From the given realization of the Bernoulli counting process, N5 = 3 and N6 - N5 = X6. Hence, X6 = N6 - N5 = 5 - 3 = 2. The value of S is the largest value of n for which Nn = 3. From the given realization of the Bernoulli counting process, N3 = 1, N4 = 2, N5 = 3, and N6 = 5. Hence, the value of S is 5.
The value of T2 is the time at which the second success occurs. From the given realization of the Bernoulli counting process, N2 = 1. Hence, the time at which the second success occurs is T2 = 2.d) P{N2=1, Ns=3, N7-4} = P{N2=1} × P{Ns-N2=2} × P{N7-Ns=1} × P{No=4}.Using the Bernoulli counting process, the probability of a success is p = 0.2 and the probability of a failure is q = 1 - p = 0.8. Therefore, P{N2=1} = pq, P{Ns-N2=2} = p²q, P{N7-Ns=1} = pq², and P{No=4} = p³.Thus, P{N2=1, Ns=3, N7-4} = (0.2)(0.8)(0.2²)(0.8)(0.2)(0.8²)(0.2³) = 0.0016384. A Bernoulli counting process is a stochastic process that consists of a sequence of independent and identically distributed random variables, where each random variable takes the value 1 or 0 with probability p and q = 1 - p, respectively. The Bernoulli counting process is often used to model the arrival times of events that occur randomly over time. The Bernoulli counting process has many applications in areas such as reliability theory, queueing theory, and inventory management.In this question, we are given the realization of a Bernoulli counting process, and we are asked to find various quantities associated with this process. We are first asked to find the value of X6, which is the number of successes that occur between times 5 and 6. We are then asked to find the value of S, which is the largest time at which three successes have occurred. We are also asked to find the value of T2, which is the time at which the second success occurs. Finally, we are asked to find the probability of a specific sequence of events occurring, given that the success probability is p = 0.2.To find the value of X6, we simply subtract the value of N5 from the value of N6. Similarly, to find the value of S, we look for the largest time at which Nn = 3. To find the value of T2, we look for the time at which N2 = 1. Finally, to find the probability of a specific sequence of events occurring, we use the probabilities of success and failure to calculate the probability of each event occurring, and then multiply these probabilities together. Thus, we have found the value of X6, the value of S, the value of T2, and the probability of a specific sequence of events occurring.
In conclusion, the Bernoulli counting process is a powerful tool for modeling the arrival times of events that occur randomly over time. By using the probabilities of success and failure, we can calculate various quantities associated with this process, such as the value of X6, the value of S, the value of T2, and the probability of a specific sequence of events occurring. The Bernoulli counting process has many applications in areas such as reliability theory, queueing theory, and inventory management.
To learn more about Bernoulli counting process visit:
brainly.com/question/24232842
#SPJ11
Q3. Arrivals of oil tankers at a port are distributed according to a Poisson distribution with a mean of four per 12 hours. ( 20 marks) a. What is the probability that in a given 12 hours no oil tanker will arrive at the port? b. What is the probability that fewer than three oil tankers will arrive in a whole day?
Answers
a) The probability that no oil tanker will arrive at the port in a given 12 hours is approximately 0.01832.
b). The probability that fewer than three oil tankers will arrive in a whole day is approximately 0.013735.
Thereforea) In a Poisson distribution, the mean (λ) is equal to the expected number of events occurring in a given interval. Here, the mean is 4 per 12 hours, so λ = 4.
P(X = 0) = (e^(-λ) × λ^0) / 0!
e is the base of the natural logarithm (approximately 2.71828) and 0! is equal to 1.
So,
P(X = 0) = (e^(-4) × 4^0) / 0!
= e^(-4) / 1
= 0.01832
b. Probability that fewer than three oil tankers will arrive in a whole day:
Since we are considering a whole day, which is 24 hours, we need to adjust the mean accordingly. The average number of oil tanker arrivals per 24 hours would be twice the mean for 12 hours, so the new mean (λ) is 2 × 4 = 8.
Now, we can find the probability of having fewer than three oil tanker arrivals (X < 3) in a whole day. This includes the probabilities of X = 0, X = 1, and X = 2.
P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2).
Using the Poisson probability mass function for each case:
P(X = 0) = (e^(-8) × 8^0) / 0!
= e^(-8) / 1
≈ 0.000335.
P(X = 1) = (e^(-8) × 8^1) / 1!
= e^(-8) × 8
≈ 0.00268.
P(X = 2) = (e^(-8) × 8² / 2!
= e(-8) × 8²/ 2
≈ 0.01072.
Adding these probabilities together:
P(X < 3) ≈ 0.000335 + 0.00268 + 0.01072
≈ 0.013735.
Learn more about Poisson distribution here
https://brainly.com/question/30388228
#SPJ4
Let's solve the problem step by step:
a. Probability of no oil tanker arrivals in a given 12 hours:
The given scenario follows a Poisson distribution with a mean of four per 12 hours. The probability mass function (PMF) of a Poisson distribution is given by:
P(X = k) = (e^(-λ) * λ^k) / k!
Where X is the random variable representing the number of oil tanker arrivals, λ is the mean (4 in this case), and k is the number of arrivals.
To find the probability of no oil tanker arrival (k = 0), we substitute k = 0 into the PMF:
P(X = 0) = (e^(-4) * 4^0) / 0!
P(X = 0) = e^(-4) / 1
P(X = 0) = e^(-4)
Therefore, the probability that no oil tanker will arrive at the port in a given 12 hours is approximately e^(-4) or approximately 0.0183 (rounded to four decimal places).
b. Probability of fewer than three oil tankers arriving in a whole day:
Since we want to calculate the probability for a whole day, we need to consider the Poisson distribution for a 24-hour period.
To find the probability of fewer than three oil tanker arrivals (k < 3), we calculate the sum of probabilities for k = 0, 1, and 2:
P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2)
Using the Poisson PMF, we can calculate each term:
P(X = 0) = e^(-4) / 0!
P(X = 1) = e^(-4) * 4^1 / 1!
P(X = 2) = e^(-4) * 4^2 / 2!
Substituting the values, we get:
P(X < 3) = e^(-4) + e^(-4) * 4 + e^(-4) * 4^2 / 2!
Calculating the factorials:
2! = 2
2! = 2 * 1 = 2
Simplifying further:
P(X < 3) = e^(-4) + 4e^(-4) + 16e^(-4) / 2
P(X < 3) = (1 + 4 + 16)e^(-4) / 2
P(X < 3) = 21e^(-4) / 2
Therefore, the probability that fewer than three oil tankers will arrive in a whole day is approximately 21e^(-4)/2 or approximately 0.2381 (rounded to four decimal places).
Note: In both parts, we used the Poisson distribution formula to calculate the probabilities based on the mean and the specific value of interest.
Learn more about Poisson Distribution from the given link
https://brainly.com/question/9123296
#SPJ11
Henry wants to double a cake recipe that uses 2 cups and 10 tbsp of flour. How much flour will he need?
Answers
9514 1404 393
Answer:
5 cups and 4 tbsp
Step-by-step explanation:
Double the quantity (2 c, 10 T) is ...
2 × (2 c, 10 T) = (4 c, 20 T)
A cup is equal to 16 tablespoons, so this quantity can be rewritten as ...
(5 c, 4 T)
Five cups and four tablespoons of flour are needed for the double recipe.
Simplified awnser
1/2 a2 - 3 x b + 2c
Answers
The given expression is a simplified algebraic equation: (1/2) * a^2 - 3b + 2c. It represents a combination of variables a, b, and c with their respective coefficients.
What is an Algebraic Equation?Utilizing symbols and operations, an algebraic equation illustrates the equivalence or inequivalence of two expressions. These generated expressions may hold variables that have varying values.
The premise centered around calculus is to arrive at a solution by acquiring the correct value(s) of these variable(s), ultimately fulfilling the outlined specification in the problem. Algebraic equations can range from uncomplicated linear problems to elaborate polynomials and trigonometric functions.
Read more about algebraic equations here:
https://brainly.com/question/2164351
#SPJ1