Answers
Answer:
2/9, 4/7, 3/5, 2/3
Step-by-step explanation:
4/7=about 0.57, 3/5 is 0.4, 2/3 is about 0.66, and 2/9 is about 0.22, so we can do 0.22, 0.57, 0.66, and 0.4 in that order
Related Questions
What is the quotient?
(-3)^0 / (-3)^2 = ?
A: -9
B: -1/9
C: 1/9
D: 9
Answers
Answer:
Step-by-step explanation:
Quotient means result of division
anything raised to 0 is 1
(-3)^0 = 1
(-3)^2 = -3 * -3 = 9
Quotient = 1/9
Answer:
1/9
Step-by-step explanation:
A political polling agency wants to take a random sample of registered voters and ask whether or not they will vote for a certain candidate. One plan is to select 400 voters, another plan is to select 1,600 voters. If the study were conducted repeatedly (selecting different samples of people each time), which one of the following would be true regarding the resulting sample proportions of "yes" responses?
A. Different sample proportions would result each time, but for sample size 400 they would be centered (have their mean) at the true population proportion, whereas for sample size 1,600 they would not.
B. Different sample proportions would result each time, but for sample size 1,600 they would be centered (have their mean) at the true population proportion, whereas for sample size 400 they would not.
C. Different sample proportions would result each time, but for either sample size, they would be centered (have their mean) at the true population proportion.
D. For either sample size, using the same size each time, as long as the samples are drawn with replacement, they would be centered (have a mean) at 0.
Answers
Answer:
C. Different sample proportions would result each time, but for either sample size, they would be centered (have their mean) at the true population proportion.
Step-by-step explanation:
From the given information;
A political polling agency wants to take a random sample of registered voters and ask whether or not they will vote for a certain candidate.
A random sample is usually an outcome of any experiment that cannot be predicted before the result.
SO;
One plan is to select 400 voters, another plan is to select 1,600 voters
If the study were conducted repeatedly (selecting different samples of people each time);
Different sample proportions would result each time, but for either sample size, they would be centered (have their mean) at the true population proportion. This is because a sample proportion deals with random experiments that cannot be predicted in advance and they are quite known to be centered about the population proportion.
Jiefei deposits money in an account paying i^{(4)}=7.125 % . How many years until she has at least doubled her initial investment. a. 18 years b. 17 years c. 15 years d. 10 years e. 14 years
Answers
The correct answer is d. 10 years.
To find out how many years it will take for Jiefei to double her initial investment, we can use the compound interest formula:
A = P(1 + r/n)^(nt)
Where:
A = final amount
P = initial investment
r = interest rate (in decimal form)
n = number of times interest is compounded per year
t = number of years
In this case, Jiefei's initial investment will double, so the final amount (A) will be 2 times her initial investment (P). The interest rate (r) is given as 7.125%, which is equivalent to 0.07125. Since the interest is compounded annually, n = 1.
So the equation becomes:
2P = P(1 + 0.07125/1)^(1*t)
Simplifying the equation:
2 = (1 + 0.07125)^t
Taking the natural logarithm of both sides:
ln(2) = ln(1 + 0.07125)^t
Using the logarithmic property:
ln(2) = t * ln(1 + 0.07125)
Solving for t:
t = ln(2) / ln(1 + 0.07125)
Using a calculator:
t ≈ 9.95 years
Rounding up to the nearest whole number, it will take approximately 10 years for Jiefei to double her initial investment.
To know more about initial investment, visit:
https://brainly.com/question/31635721
#SPJ11
Mary is determining the maximum quantity given the seasonality is constant. If the coefficients are 117t and −22.9906t
2
in a quadratic model, what is the maximum quantity that can be reached? 12.52 B 3 0.098 5.09
Answers
The maximum quantity that can be reached in a quadratic model can be determined by finding the vertex of the quadratic function. In this case, with coefficients of 117t and -22.9906t^2, the maximum quantity can be calculated.
To find the maximum quantity in a quadratic model, we need to locate the vertex of the quadratic function. The vertex is the point where the quadratic curve reaches its maximum or minimum value. In a quadratic equation of the form ax^2 + bx + c, the x-coordinate of the vertex can be found using the formula x = -b / (2a). In this case, the coefficients of the quadratic model are 117t and -22.9906t^2. Since there is no constant term, we can disregard it in this calculation. By substituting the values into the formula, we find that the x-coordinate of the vertex is -117 / (2 * -22.9906) = 2.5415.
To determine the maximum quantity, we need to substitute this value back into the quadratic equation. However, since the problem statement does not provide the complete quadratic equation or the context for the variable t, we cannot calculate the exact maximum quantity. Therefore, the specific value of the maximum quantity cannot be determined without additional information.
Learn more about quadratic here:
https://brainly.com/question/22364785
#SPJ11
Which number line represents the solution set for the inequality 2x - 62 6(x - 2) + 8?
-15
-0.5
0
0.5
1
1.5
-1.5
-1
-0.5
0
0.5
1.5
-1.5
-1
-0.5
0
0.5
1.5
-1.5
-1.5
0
0.5
1
1.5

Answers
Answer:
2x - 6 ≥ 6(x-2) + 8
2x - 6 ≥ 6x - 12 + 8
6x - 2x ≤ - 6 + 4
4x ≤ -2
4x/4 ≤ -2/4
x ≤ -1/2
Interval Notation: (- ∞, -1/2]
The line starts from -1/2 with the arrow going to the left (decreasing). The endpoint or value from where it started, which is -1/2, should be shaded. The inequality symbol x ≤ -1/2 represents the values at most or maximum -1/2.
Step-by-step explanation:
The number line representing the solution set for the inequality given is option C.
The inequality is 2x - 6 ≥ 6(x-2) + 8,
Solving for x,
2x - 6 ≥ 6(x-2) + 8
2x - 6 ≥ 6x - 12 + 8
6x - 2x ≤ - 6 + 4
4x ≤ -2
4x/4 ≤ -2/4
x ≤ -1/2
Therefore, the Interval Notation is (- ∞, -1/2]
This means that the all the values of x will be less than -1/2 or equal to it,
Therefore, the graph will be, the line starts from -1/2 with the arrow going to the left (decreasing).
Learn more about inequality, click;
https://brainly.com/question/30231190
#SPJ7
Analytically show that the equations below represent trigonometric identity statements. 1. sec²θ (1-cos²θ) 2. cosx(secx-cosx) = sin²x 3. cosθ + sinθtanθ = secθ 4. (1- cos∝)(cosec∝+cot∝)= cos∝ tan∝
Answers
To show that the given equations represent trigonometric identity statements, we will simplify each equation and demonstrate that both sides of the equation are equal.
Starting with sec²θ(1 - cos²θ):
Using the Pythagorean identity sin²θ + cos²θ = 1, we can rewrite sec²θ as 1 + tan²θ. Substituting this into the equation, we get:
(1 + tan²θ)(1 - cos²θ)
= 1 - cos²θ + tan²θ - cos²θtan²θ
= 1 - cos²θ(1 - tan²θ)
= sin²θ
Thus, the equation simplifies to sin²θ, which is a trigonometric identity.
For cosx(secx - cosx) = sin²x:
Using the reciprocal identities secx = 1/cosx and tanx = sinx/cosx, we can rewrite the equation as:
cosx(1/cosx - cosx)
= cosx/cosx - cos²x
= 1 - cos²x
= sin²x
Hence, the equation simplifies to sin²x, which is a trigonometric identity.
Considering cosθ + sinθtanθ = secθ:
Dividing both sides of the equation by cosθ, we obtain:
1 + sinθ/cosθ = 1/cosθ
Using the identity tanθ = sinθ/cosθ, the equation becomes:
1 + tanθ = secθ
This is a well-known trigonometric identity, where the left side is equal to the reciprocal of the right side.
Simplifying (1 - cos∝)(cosec∝ + cot∝):
Expanding the expression, we have:
cosec∝ - cos∝cosec∝ + cot∝ - cos∝cot∝
= cot∝ - cos∝cot∝ + cosec∝ - cos∝cosec∝
= cot∝(1 - cos∝) + cosec∝(1 - cos∝)
= cot∝tan∝ + cosec∝sec∝
= 1 + 1
= 2
Thus, the equation simplifies to 2, which is a constant value.
In summary, we have analytically shown that the given equations represent trigonometric identity statements by simplifying each equation and demonstrating that both sides are equal.
To learn more about trigonometric identities click here: brainly.com/question/24377281
#SPJ11.
Decide whether the following statement is compound if lana wins the election then mary will smile
Answers
The correct answer is OD. Although the word "then" appears in the statement, it is not used as a logical connective. So the statement is not compound.
The statement "If Laura sells her quota, then Marie will be happy" is a single declarative sentence. It consists of a conditional clause ("If Laura sells her quota") and a consequent clause ("then Marie will be happy"). However, these two clauses are not independent statements that can stand alone. Instead, they are connected in a cause-and-effect relationship. The word "then" in this context is not functioning as a logical connective, but rather as an indicator of the consequent clause.
A compound statement is formed by combining two or more independent statements using logical connectives such as "and," "or," or "if...then." In the given statement, there is no logical connective joining two independent statements.
Therefore, the statement is not compound.
Learn more about compound statement click;
https://brainly.com/question/5429065
#SPJ4
The price of an item has been reduced by $2.58.The original price was $17.84.What is the price now?
Answers
Answer:
$15.26
Step-by-step explanation:
First, 17.84 - 2.58 = 15.26
Hope this helps!
construct a geometric figure that illustrates why a line in r2 not through the origin is not closed under vector addition
Answers
A line in ℝ² that does not pass through the origin is not closed under vector addition because vector addition can produce vectors that do not lie on the original line.
To illustrate why a line in ℝ² that does not pass through the origin is not closed under vector addition, we can consider the following example:
Let's take a line in ℝ² given by the equation y = x + 1, which does not pass through the origin (0, 0).
Now, suppose we have two vectors on this line: A = (1, 2) and B = (2, 3).
If we add these two vectors, A + B, we get (1, 2) + (2, 3) = (3, 5).
Now, let's examine the resulting vector (3, 5). Since the line y = x + 1 does not pass through the origin, (0, 0) is not on this line. However, (3, 5) lies on the line y = x + 1.
Therefore, the resulting vector (3, 5) is not on the original line y = x + 1.
This demonstrates that the line is not closed under vector addition because the addition of vectors from the line can result in a vector that is not on the line.
In conclusion, a line in ℝ² that does not pass through the origin is not closed under vector addition because vector addition can produce vectors that do not lie on the original line.
To know more about vector addition refer here:
https://brainly.com/question/28875206#
#SPJ11
Write 30/42 in lowest terms.
Answers
Answer:
0.71428571428
Step-by-step explanation:
30 divided by 42 = 0.71428571428
Please give decent explanation ty.

Answers
Answer: 20 / 29
Step-by-step explanation:
cos is defined as adjacent over hypotenuse, which simplified means whatever side that its touching over the side that is diagonal. In this case, P is touching 20, and the hypotenuse is 29, therefore the answer is 20/29
In a clinical trial to test a vaccine's effectiveness, the researchers report a slight reduction in the percentage of those catching the virus in comparison to those in a control group, and publish a p-value of 0.23. What is the best interpretation of this value
Answers
A p-value of 0.23 in the context of a clinical trial testing a vaccine's effectiveness suggests that the observed reduction in the percentage of individuals catching the virus, when comparing the vaccine group to the control group, is not statistically significant at conventional levels of significance (such as 0.05 or 0.01).
The p-value represents the probability of obtaining the observed data, or data more extreme, under the assumption that the null hypothesis is true.
In this case, the null hypothesis would typically state that there is no difference in the percentage of virus cases between the vaccine and control groups. A p-value of 0.23 indicates that there is a 23% chance of observing the reported reduction in cases or an even more substantial reduction if the null hypothesis were true.
Therefore, based solely on the p-value of 0.23, the best interpretation is that the observed reduction in virus cases could plausibly be due to random variation or chance, rather than a true effect of the vaccine. However, it is important to consider other factors, such as the study design, sample size, and clinical significance of the observed reduction, before drawing final conclusions about the vaccine's effectiveness.
To know more about reduction visit-
brainly.com/question/16693489
#SPJ11
i will give you brainlist for for the first person who answered this question but i dont know how you are going to answer it?

Answers
Answer:
Here :)
Step-by-step explanation:

Anthony bought 4 1/2 pounds of meatballs. He decided to cook 1 1/4 pounds and freeze the rest. How many pounds did he freeze
Answers
Answer:
anthony froze 3 1/4 of the meatball
HELP, WILL GIVE BRAINLIEST!!
Find two possible lengths for CD if C, D, and E are collinear, CE = 14.5 cm, and DE = 2.4 cm.
Answers
Answer:
12.3 cm and 19.3 cm
in the figure below, 33 of the 66 disks are to be painted blue, 22 are to be painted red, and 11 is to be painted green. two paintings that can be obtained from one another by a rotation or a reflection of the entire figure are considered the same. how many different paintings are possible?
Answers
The number of different paintings possible for the given figure is (3^66 + 3) / 6. after rotation.
To determine the number of different paintings possible, we need to consider the symmetries of the figure and apply the concept of Burnside's Lemma.
In this case, we have a figure with 66 disks that are to be painted in three different colors: blue, red, and green. We want to count the number of different paintings that can be obtained by rotating or reflecting the entire figure.
Let's analyze the symmetries of the figure:
1. Identity (no rotation or reflection): This symmetry leaves all the disks in their original positions. There is only one way to paint the figure in this case.
2. Rotation by 120 degrees clockwise: This symmetry can be achieved by rotating the figure one-third of a full rotation. Since we have three colors, each disk can be painted in any of the three colors independently. Therefore, there are 3^66 possible paintings that remain the same under this rotation.
3. Rotation by 240 degrees clockwise: This symmetry can be achieved by rotating the figure two-thirds of a full rotation. Similar to the previous case, there are 3^66 possible paintings that remain the same under this rotation.
4. Reflection along a vertical axis: This symmetry can be achieved by flipping the figure horizontally. Since the figure has an even number of disks, the reflection will result in the same pattern. Therefore, there is only one way to paint the figure that remains the same under this reflection.
5. Reflection along a horizontal axis: This symmetry can be achieved by flipping the figure vertically. Similar to the previous case, there is only one way to paint the figure that remains the same under this reflection.
6. Reflection along the main diagonal: This symmetry can be achieved by reflecting the figure along the main diagonal (from the top left to the bottom right). Again, since the figure has an even number of disks, the reflection will result in the same pattern. Therefore, there is only one way to paint the figure that remains the same under this reflection.
7. Reflection along the secondary diagonal: This symmetry can be achieved by reflecting the figure along the secondary diagonal (from the top right to the bottom left). Similar to the previous case, there is only one way to paint the figure that remains the same under this reflection.
Applying Burnside's Lemma, the number of distinct paintings is given by the average number of fixed points (paintings that remain the same) under each symmetry. Therefore, the total number of distinct paintings is:
(1 + 3^66 + 3^66 + 1 + 1 + 1) / 6 = (3^66 + 3) / 6
Calculating this expression may not be feasible due to the large exponent. Therefore, it is recommended to use a calculator or computer program to obtain the numerical value.
In conclusion, the number of different paintings possible for the given figure is (3^66 + 3) / 6.
for more such question on rotation visit
https://brainly.com/question/2078551
#SPJ8
Fencing costs $5.45 per foot and sod costs o.65 per square foot. to allow for measurements error, cartwr plans to but and estra 10 percent of both material. how much will it cost carter to purchase the materials
Answers
The most appropriate choice for percentage will be given by
Cost of fencing 1.1 foot = $5.995
Cost of sodding 1.1 sq. foot = $0.715
Total cost of fencing and sodding = $6.71
What is percentage?
Suppose there is a number and the number has to be expressed as a fraction of 100. The fraction is called percentage.
For example- 2% means \(\frac{2}{100}\)
Here,
Cost of fencing 1 foot = $5.45
10% of 1 foot = \(\frac{10}{100}\times 1\)
= 0.1 foot
1 foot + 10% of 1 foot = 1 + 0.1 = 1.1 feet
cost of fencing 1.1 foot = $5.45 \(\times\) 1.1 = $5.995
Cost of sodding 1 sq foot = $0.65
Cost of sodding 1.1 sq foot = $0.65 \(\times\) 1.1 = $0.715
Total cost of fencing and sodding = $(5.995 + 0.715)
= $6.71
To learn more about percentage, refer to the link-
https://brainly.com/question/843074
#SPJ4
is -4x-8=4x+8 one solution no solution or many solutions
Answers
-8x=-16
x=-2
Answer:
One solution.
Step-by-step explanation:
This question has different coefficients so it has one solution.
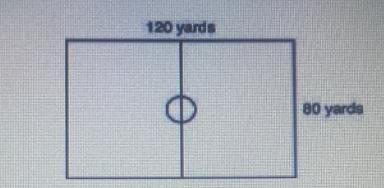
located in the middle of the field has a circumference of 16π yards. A diagram of the soccer field is shown below. What is the area, in square yards, of the portion of the field that is outside of the circular area?
Answers
The portion of the field that is outside of the circular area is 9,398.4 yd².
What is the area of the circular portion?The radius of the circle is calculated as follows;
circumference of the circle = 16π yards
circumference = 2πr
where;
r is the radius of the circle2πr = 16π
r = 8 yards
The area of the circular portion is calculated as follows;
A = πr²
A = π x (8 yd)²
A = 201.6 yd²
The total area of the field is calculated as follows;
A = 120 yds x 80 yds
A = 9,600 yd²
The portion of the field that is outside of the circular area is calculated as follows;
= 9,600 yd² - 201.6 yd²
= 9,398.4 yd²
Learn more about area of field here: https://brainly.com/question/16655158
#SPJ1
PLEASE HELP!!! I REALLY NEED IT!!!
So, this is kind of random, but can someone give, like, a step-by-step explanation of how to do this equation?
(22+(-6/20)) * (214-10(-6/20)) - (284.75)=4424.15
Thank you so much, I just... I cannot will myself to figure out this problem today. Love youuu!
Answers
Step-by-step explanation:
(22 + (-6/20) × (214 - 10 ( -6/20)) - (284.75)
(22 - 6/20) × (214 + 60/20) - (284.75)
(22 - 0.3) × (214 + 3) - (284.75)
(21.7 × 217) - 284.75
4708.9 - 284.75
= 4424.15
why is it necessary to apply the finite population correction factor when a sample is a significant part of the population?
Answers
It necessary to apply the finite population correction factor (FPC) when a sample is a significant part of the population because for more than 5% of finite population the standard error in the estimated value will come to be too big.
The formula of FPC is
FPC =\(\sqrt{ (N-n)/(N-1)}\)
where N= population size
n= sample size
To know more about finite population correction factor
https://brainly.com/question/2114699
#SPJ4
The equation of a line is given below.
6x+2y=4
Find the slope and the y-intercept. Then use them to graph the line

Answers
Hence, in answering the stated question, we may say that We can travel slope intercept down 3 units and right 1 unit to acquire another point on the line because the slope is -3.
what is slope intercept?The intersection point in mathematics is the point on the y-axis where the slope of the line intersects. a point on a line or curve where the y-axis intersects. The equation for the straight line is Y = mx+c, where m represents the slope and c represents the y-intercept. The intercept form of the equation emphasises the line's slope (m) and y-intercept (b). The slope of an equation with the intercept form (y=mx+b) is m, and the y-intercept is b. Several equations can be reformulated to seem to be slope intercepts. When y=x is represented as y=1x+0, the slope and y-intercept are both set to 1.
We must solve for y in order to find the slope-intercept form of the equation:
6x + 2y = 4
2y = -6x + 4
y = -3x + 2
As a result, the slope is -3 and the y-intercept is 2.
To graph the line, first plot the y-intercept at the point (0, 2). The slope can then be used to find another point on the line. We can travel down 3 units and right 1 unit to acquire another point on the line because the slope is -3.
To know more about slope intercept visit:
https://brainly.com/question/19824331
#SPJ1
© macmillan learning the national center for health statistics (nchs) reports that 70% of u.s. adults aged 65 and over have ever received a pneumococcal vaccination. suppose that you obtain an independent sample of 20 adults aged 65 and over who visited the emergency room and the pneumococcal vaccination rate applies to the sample. determine the probability that exactly 14 members of the sample received a pneumococcal vaccination. let ???? represent the number of successes in a binomial setting with ???? trials and probability p of success in each trial. the probability of obtaining exactly ???? successes is given by the formula P(????
Answers
The probability of exactly 14 members out of a sample of 20 adults aged 65 and over receiving a pneumococcal vaccination can be determined using the binomial probability formula.
In this scenario, we are dealing with a binomial setting, where we have a fixed number of trials (20 adults in the sample) and two possible outcomes for each trial (either receiving or not receiving a pneumococcal vaccination). The probability of success, denoted as "p," is the proportion of U.S. adults aged 65 and over who have received the vaccination, which is 70% or 0.7 in this case.
To find the probability of exactly 14 successes, we can use the binomial probability formula:
P(X = 14) = C(n, x) * \(p^x\) * \((1 - p)^{(n - x)}\)
Here, C(n, x) represents the binomial coefficient, which calculates the number of ways to choose x successes out of n trials. In this case, n = 20 and x = 14.
Calculating the probability:
P(X = 14) = C(20, 14) * \(0.7^{14}\)* \((1 - 0.7)^{(20 - 14)}\)
Using the binomial coefficient formula C(n, x) = n! / (x!(n - x)!), we can find the value of C(20, 14) to be 38760.
Substituting the values, we get:
P(X = 14) = 38760 * \(0.7^{14}\) * \(0.3^6\)
Evaluating this expression will give us the probability that exactly 14 members of the sample received a pneumococcal vaccination.
Learn more about probability here:
https://brainly.com/question/33177801
#SPJ11
julio is drawing tiles from a bag of tiles from a bag of tiles like the ones shown below. he draws a tile, replaces it, and draws another tile. what is the probability he willl draw a red tile on both draws?
Answers
The probability of drawing a red tile on both draws would be (r/n) * (r/n) = r²/n².
To determine the probability of drawing a red tile on both draws, we need to know the number of red tiles and the total number of tiles in the bag. However, the description does not provide this information. If we assume that there are n total tiles in the bag, with r of them being red, the probability of drawing a red tile on the first draw would be r/n. Since the tile is replaced before the second draw, the probability of drawing another red tile would also be r/n.
Therefore, the probability of drawing a red tile on both draws would be (r/n) * (r/n) = r²/n². Without knowing the specific values of r and n, we cannot determine the exact probability.
To learn more about probability click here: brainly.com/question/31828911
#SPJ11
Which procedure justifies whether Negative 3 x (5 minus 4) + 3 (x minus 6) is equivalent to Negative 12 x minus 6? The expressions are not equivalent because Negative 3 (2) (5 minus 4) + 3 (2 minus 6) = negative 18 and Negative 12 (2) minus 6 = negative 30. The expressions are not equivalent because Negative 3 (2) (5 minus 4) + 3 (2 minus 6) = negative 18 and Negative 12 (3) minus 6 = negative 42. The expressions are equivalent because Negative 3 (2) (5 minus 4) + 3 (2 minus 6) = negative 18 and Negative 12 (negative 2) minus 6 = 18. The expressions are equivalent because Negative 3 (2) (5 minus 4) + 3 (2 minus 6) = negative 18 and Negative 12 (1) minus 6 = negative 18
Answers
Answer:
Yes, the expressions are equivalent
Step-by-step explanation:
Let's check it out:
=> -3x(5-4)+3(x-6)
Expanding brackets using distributive property.
=> -15x+12+3x-18
Combining like terms
=> -15x+3x+12-18
=> -12x-6
Yes, the expression is equivalent to -12x-6
Answer:
its A
Step-by-step explanation:
i took the test
1+2-3+0-1039+2-2/2/2/2/2/-21/3/6/7/8/4/2/34/6/6/1000000-10202*2020
answer noobs
Answers
Answer:
If im not wrong it should be -20609077.125000000002128
Step-by-step explanation:
if im wrong im sorry (-///////-)
Katerina's phone number has ten digits in total. Now her friend Kylie wants to call her, but Kylie only remembers the first six digits. How many times Kylie has to try at most in order to call Katerina if she does not dial repetitive phone numbers?
Answers
Kylie has to try at most 3,024 different combinations in order to call Katerina if she does not dial repetitive phone numbers.
Kylie only recalls the first six numbers of Katerina's phone number, so she must guess the last four. Because she cannot repeat any of the numbers she has already successfully predicted, the first remaining digit has just nine viable alternatives (all digits from 0 to 9 except the one she already knows). Similarly, the second remaining digit has just eight options, the third has seven, and the fourth has six.
Therefore, the total number of possible combinations is:
9 x 8 x 7 x 6 = 3,024
This implies Kylie will have to try at most 3,024 different combinations to reach Katerina, provided she gets it right on the last try.
Learn more about Combination:
https://brainly.com/question/30450879
#SPJ4
Multisets, or bags, can be represented as list of pairs (x,n) where n indicates the number of occurrences of x in the multiset. type Bag a=[(a,Int)] For the following exercises you can assume the following properties of the bag representation. But note: Your function definitions have to maintain these properties for any multiset they produce! (1) Each element x occurs in at most one pair in the list. (2) Each element that occurs in a pair has a positive counter. As an example consider the multiset {2,3,3,5,7,7,7,8}, which has the following representation (among others). [(5,1),(7,3),(2,1),(3,2),(8,1)] Note that the order of elements is not fixed. In particular, we cannot assume that the elements are sorted. Thus, the above list representation is just one example of several possible. d) Define a function subbag that determines whether or not its first argument bag is contained in the second. subbag :: Eq a ⇒ Bag a → Bag a → Bool Note that a bag b is contained in a bag b.
if every element that occurs n times in b occurs also at least n times in b
Answers
We're using `count` as a helper function to count the number of times the first bag appears in the second.
Multisets, also known as bags, can be represented as a list of pairs (x,n) in which n indicates the number of times x appears in the multiset.
Type bag `a=[(a,Int)]` is a set of this kind.
In the following activities, the bag representation's following characteristics can be considered.
However, your function definitions must maintain these characteristics for any multiset they create! 1.
In the list, each component x appears in at most one pair.
2. Each element that occurs in a pair has a positive counter.
A bag contains a bag b if every element that appears n times in b appears at least n times in
b. This function can be defined as follows:
```subbag:: Eq a => Bag a -> Bag a -> Boolsubbag [] _ = Truesubbag _ [] = Falsesubbag ((a,n):xs) b = if (n > count a b) then False else subbag xs b
where count a [] = 0count a ((b,m):ys) = if (a==b) then m else count a ys```Note:
Here, `subbag` is a recursive function that takes two bags as its input and returns a Boolean value indicating whether or not the first bag is included in the second.
We're using `count` as a helper function to count the number of times the first bag appears in the second.
Know more about a function here:
https://brainly.com/question/22340031
#SPJ11
(1 point) suppose we want a 90% confidence interval for the average amount spent on books by freshmen in their first year at college. the amount spent has a normal distribution with standard deviation $33. (a) how large should the sample be if the margin of error is to be less than $4?
Answers
48630 is large should the sample be if the margin of error is to be less than $4 .
What does the term "margin of error" mean?
A margin of error is a statistical term that takes into account the discrepancy between the outcomes of a random survey sample and the expected results. Simply put, you can determine how unpredictable data and research results are by looking at the margin of error.Margin of Error = Z*Stdev/sqrt(n)
4 <= 0.90* 33/sqrt(n)
n >= (0.90* 33/2)^4 = 48630.17 OR 48630
So, n should be atleast 48630 so that margin of error is within $4
Learn more about Margin of Error
brainly.com/question/10501147
#SPJ4
mrs. washington's class has x student. Three-fourths of these students like pizza.If 21 students in the class like pizza, which equation can be solved to determine the number of students in the class?
A. 21x = 3/4
B. 21x = 4/3
C. 4/3x = 21
D.3/4x = 21
